Statistiques - Transformations
La transformation de données fait référence à l'application d'une fonction à chaque élément d'un ensemble de données. Ici, $ x_i $ est remplacé par sa valeur transformée $ y_i $ où $ y_i = f (x_i) $. Les transformations de données sont généralement effectuées pour rendre l'apparence des graphiques plus interprétable.
Il existe quatre fonctions principales utilisées pour les transformations.
$ log x $- transformations logarithmiques. Par exemple, les unités sonores sont en décibels et sont généralement représentées à l'aide de transformations log.
$ \frac{1}{x} $- Transformations réciproques. Par exemple, le temps pour terminer la course / tâche est représenté en utilisant la vitesse. Plus la vitesse, moins le temps nécessaire.
$ \sqrt{x} $- Transformations de racine carrée. Par exemple, les zones de terrain circulaire sont comparées en utilisant leur rayon.
$ {x^2} $- Transformations de puissance. Par exemple pour comparer des nombres négatifs.
Les transformations logarithme et racine carrée sont utilisées dans le cas de nombres positifs alors que les transformations réciproques et de puissance peuvent être utilisées dans le cas de nombres négatifs et positifs.
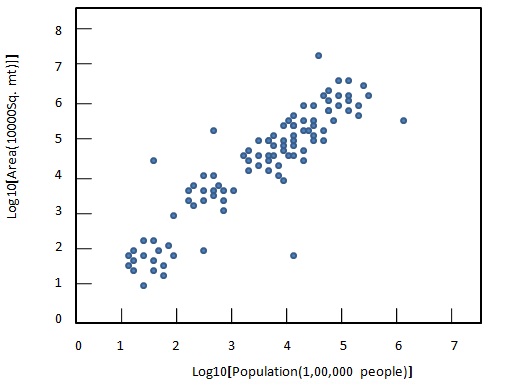
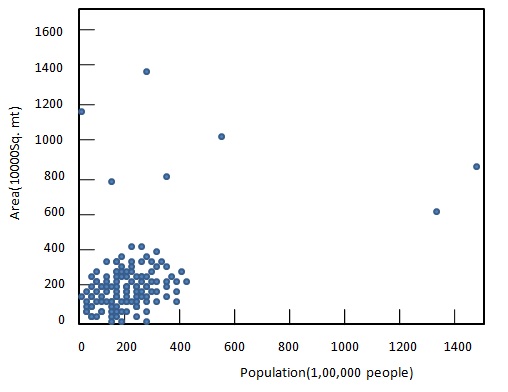
Les diagrammes suivants illustrent l'utilisation de la transformation logarithmique pour comparer graphiquement la population.
Before transformation
After transformation