Statistiques - Distribution Gamma

La distribution gamma représente les distributions de probabilité continues d'une famille à deux paramètres. Les distributions gamma sont conçues avec généralement trois types de combinaisons de paramètres.

Un paramètre de forme $ k $ et un paramètre d'échelle $ \ theta $.
Un paramètre de forme $ \ alpha = k $ et un paramètre d'échelle inverse $ \ beta = \ frac {1} {\ theta} $, appelé comme paramètre de taux.
Un paramètre de forme $ k $ et un paramètre moyen $ \ mu = \ frac {k} {\ beta} $.

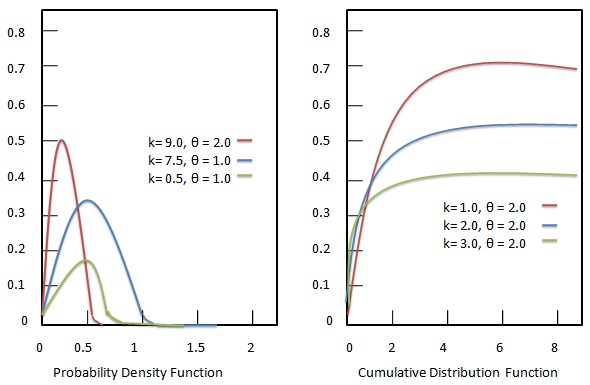
Chaque paramètre est un nombre réel positif. La distribution gamma est la distribution de probabilité d'entropie maximale déterminée par les critères suivants.

Formule

$ {E [X] = k \ theta = \ frac {\ alpha} {\ beta} \ gt 0 \ et \ est \ fixe. \\ [7pt] E [ln (X)] = \ psi (k) + ln (\ theta) = \ psi (\ alpha) - ln (\ beta) \ et \ est \ fixe. } $

Où -

$ {X} $ = variable aléatoire.
$ {\ psi} $ = fonction digamma.

Caractérisation utilisant la forme $ \ alpha $ et le taux $ \ beta $

Fonction de densité de probabilité

La fonction de densité de probabilité de la distribution gamma est donnée comme suit:

Formule

$ {f (x; \ alpha, \ beta) = \ frac {\ beta ^ \ alpha x ^ {\ alpha - 1} e ^ {- x \ beta}} {\ Gamma (\ alpha)} \ où \ x \ ge 0 \ et \ \ alpha, \ beta \ gt 0} $

Où -

$ {\ alpha} $ = paramètre d'emplacement.
$ {\ beta} $ = paramètre d'échelle.
$ {x} $ = variable aléatoire.

Fonction de distribution cumulative

La fonction de distribution cumulative de la distribution Gamma est donnée comme suit:

Formule

$ {F (x; \ alpha, \ beta) = \ int_0 ^ xf (u; \ alpha, \ beta) du = \ frac {\ gamma (\ alpha, \ beta x)} {\ Gamma (\ alpha)} } $

Où -

$ {\ alpha} $ = paramètre d'emplacement.
$ {\ beta} $ = paramètre d'échelle.
$ {x} $ = variable aléatoire.
$ {\ gamma (\ alpha, \ beta x)} $ = fonction gamma incomplète inférieure.

Caractérisation utilisant la forme $ k $ et l'échelle $ \ theta $

Fonction de densité de probabilité

La fonction de densité de probabilité de la distribution gamma est donnée comme suit:

Formule

$ {f (x; k, \ theta) = \ frac {x ^ {k - 1} e ^ {- \ frac {x} {\ theta}}} {\ theta ^ k \ Gamma (k)} \ où \ x \ gt 0 \ et \ k, \ theta \ gt 0} $

Où -

$ {k} $ = paramètre de forme.
$ {\ theta} $ = paramètre d'échelle.
$ {x} $ = variable aléatoire.
$ {\ Gamma (k)} $ = fonction gamma évaluée en k.

Fonction de distribution cumulative

La fonction de distribution cumulative de la distribution Gamma est donnée comme suit:

Formule

$ {F (x; k, \ theta) = \ int_0 ^ xf (u; k, \ theta) du = \ frac {\ gamma (k, \ frac {x} {\ theta})} {\ Gamma (k )}} $

Où -

$ {k} $ = paramètre de forme.
$ {\ theta} $ = paramètre d'échelle.
$ {x} $ = variable aléatoire.
$ {\ gamma (k, \ frac {x} {\ theta})} $ = fonction gamma incomplète inférieure.