Statistiques - Comparaison des graphiques
Les groupes de population peuvent être comparés à l'aide de diagrammes en boîte et à moustaches. La dispersion visible globale et la différence entre la médiane sont utilisées pour tirer la conclusion qu'il y a ou non une différence entre deux groupes.
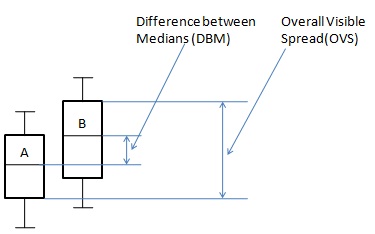
Cas 2: Formule
$ {P = \ frac {DBM} {OVS} \ fois 100} $
Où -
$ {P} $ = différence en pourcentage
$ {DBM} $ = Différence entre les médianes.
$ {OVS} $ = Spread global visible.
Règles
Pour un échantillon de 30 si ce pourcentage est supérieur à 33%, il y a généralement une différence entre deux groupes.
Pour un échantillon de 100 si ce pourcentage est supérieur à 20%, il y a généralement une différence entre deux groupes.
Pour une taille d'échantillon de 1000, si ce pourcentage est supérieur à 10%, il y a généralement une différence entre deux groupes.
Exemple
Énoncé du problème:
Décrivez la différence entre les ensembles de données suivants.
| Sr. No. | Nom | Définir A | Ensemble B |
|---|---|---|---|
| 1 | Max | 12 | 15 |
| 2 | UQ | dix | 13 |
| 3 | Médian | sept | dix |
| 4 | LQ | 6 | 9 |
| 5 | Min | 5 | 6 |
Solution:
Considérez le diagramme suivant:
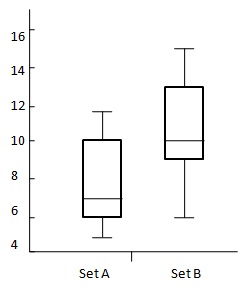
$ {OVS = 13 - 6 \\ [7pt] \ = 7 \\ [7pt] \ DBM = 10 -3 \\ [7pt] \ = 4} $
Appliquer la formule
$ {P = \ frac {DBM} {OVS} \ fois 100 \\ [7pt] \ = \ frac {4} {7} \ fois 100 \\ [7pt] \ = 57.14} $
Comme le pourcentage est supérieur à 33%, il y a donc une différence entre l'ensemble A et l'ensemble B. Il est probable que l'ensemble B soit supérieur à l'ensemble A.