Statistiques - Distribution de Poisson cumulative
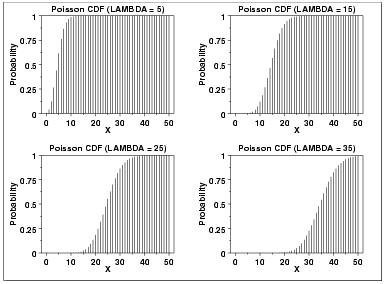
$ {\ lambda} $ est le paramètre de forme qui indique le nombre moyen d'événements dans l'intervalle de temps donné. Voici le graphique de la fonction de densité de probabilité de Poisson pour quatre valeurs de $ {\ lambda} $. Fonction de distribution cumulative.
Formule
$$ {F (x, \ lambda) = \ sum_ {k = 0} ^ x \ frac {e ^ {- \ lambda} \ lambda ^ x} {k!}} $$
Où -
$ {e} $ = La base du logarithme népérien égal à 2,71828
$ {k} $ = Le nombre d'occurrences d'un événement; dont la probabilité est donnée par la fonction.
$ {k!} $ = La factorielle de k
$ {\ lambda} $ = Un nombre réel positif, égal au nombre attendu d'occurrences pendant l'intervalle donné
Exemple
Problem Statement:
Un système logiciel complexe fait en moyenne 7 erreurs pour 5 000 lignes de code. Quelle est la probabilité d'exactement 2 erreurs sur 5 000 lignes de lignes de code sélectionnées au hasard?
Solution:
La probabilité d'exactement 2 erreurs sur 5000 lignes de lignes de code sélectionnées au hasard est: