Statistiques - Distribution exponentielle
La distribution exponentielle ou distribution exponentielle négative représente une distribution de probabilité pour décrire le temps entre les événements dans un processus de Poisson. Dans le processus de Poisson, les événements se produisent de manière continue et indépendante à un rythme moyen constant. La distribution exponentielle est un cas particulier de la distribution gamma.
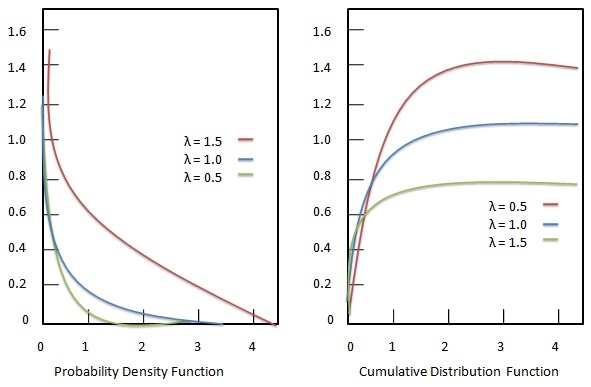
Fonction de densité de probabilité
La fonction de densité de probabilité de la distribution exponentielle est donnée comme suit:
Formule
Où -
$ {\ lambda} $ = paramètre de taux.
$ {x} $ = variable aléatoire.
Fonction de distribution cumulative
La fonction de distribution cumulative de la distribution exponentielle est donnée comme suit:
Formule
Où -
$ {\ lambda} $ = paramètre de taux.
$ {x} $ = variable aléatoire.