Cosmologia - Distanza del diametro angolare
In questo capitolo, capiremo cos'è la distanza del diametro angolare e come aiuta in cosmologia.
Per l'universo attuale -
$ \ Omega_ {m, 0} \: = \: 0.3 $
$ \ Omega _ {\ wedge, 0} \: = \: 0.69 $
$ \ Omega_ {rad, 0} \: = \: 0.01 $
$ \ Omega_ {k, 0} \: = \: 0 $
Finora abbiamo studiato due tipi di distanze:
Proper distance (lp) - La distanza percorsa dai fotoni dalla sorgente a noi, ovvero The Instantaneous distance.
Comoving distance (lc) - Distanza tra gli oggetti in uno spazio che non si espande, ovvero distance in a comoving frame of reference.
Distanza come funzione del Redshift
Considera una galassia che irradia un fotone alla volta t1 che viene rilevato dall'osservatore in t0. Possiamo scrivere la giusta distanza dalla galassia come -
$$ l_p = \ int_ {t_1} ^ {t_0} cdt $$
Lascia che sia il redshift della galassia z,
$$ \ Rightarrow \ frac {\ mathrm {d} z} {\ mathrm {d} t} = - \ frac {1} {a ^ 2} \ frac {\ mathrm {d} a} {\ mathrm {d} t} $$
$$ \ Rightarrow \ frac {\ mathrm {d} z} {\ mathrm {d} t} = - \ frac {\ frac {\ mathrm {d} a} {\ mathrm {d} t}} {a} \ frac {1} {a} $$
$$ \ quindi \ frac {\ mathrm {d} z} {\ mathrm {d} t} = - \ frac {H (z)} {a} $$
Ora, spostandosi a distanza della galassia in qualsiasi momento t sarà -
$$ l_c = \ frac {l_p} {a (t)} $$
$$ l_c = \ int_ {t_1} ^ {t_0} \ frac {cdt} {a (t)} $$
In termini di z,
$$ l_c = \ int_ {t_0} ^ {t_1} \ frac {cdz} {H (z)} $$
Esistono due modi per trovare le distanze, che sono i seguenti:
Rapporto flusso-luminosità
$$ F = \ frac {L} {4 \ pi d ^ 2} $$
dove d è la distanza alla sorgente.
La distanza del diametro angolare di una sorgente
Se conosciamo la dimensione di una sorgente, la sua larghezza angolare ci dirà la sua distanza dall'osservatore.
$$ \ theta = \ frac {D} {l} $$
dove l è la distanza del diametro angolare della sorgente.
θ è la dimensione angolare della sorgente.
D è la dimensione della sorgente.
Considera una galassia di dimensione D e dimensione angolare dθ.
Lo sappiamo,
$$ d \ theta = \ frac {D} {d_A} $$
$$ \ quindi D ^ 2 = a (t) ^ 2 (r ^ 2 d \ theta ^ 2) \ quad \ perché dr ^ 2 = 0; \: d \ phi ^ 2 \ circa 0 $$
$$ \ Rightarrow D = a (t) rd \ theta $$
Mutevole r per rc, la distanza in movimento della galassia, abbiamo -
$$ d \ theta = \ frac {D} {r_ca (t)} $$
Qui, se scegliamo t = t0, finiamo per misurare la distanza attuale dalla galassia. MaDviene misurata al momento dell'emissione del fotone. Pertanto, utilizzandot = t0, otteniamo una distanza maggiore dalla galassia e quindi una sottostima delle sue dimensioni. Pertanto, dovremmo usare il tempot1.
$$ \ quindi d \ theta = \ frac {D} {r_ca (t_1)} $$
Confrontando questo con il risultato precedente, otteniamo:
$$ d_ \ wedge = a (t_1) r_c $$
$$ r_c = l_c = \ frac {d_ \ wedge} {a (t_1)} = d_ \ wedge (1 + z_1) \ quad \ perché 1 + z_1 = \ frac {1} {a (t_1)} $$
Perciò,
$$ d_ \ wedge = \ frac {c} {1 + z_1} \ int_ {0} ^ {z_1} \ frac {dz} {H (z)} $$
dA è la distanza del diametro angolare per l'oggetto.
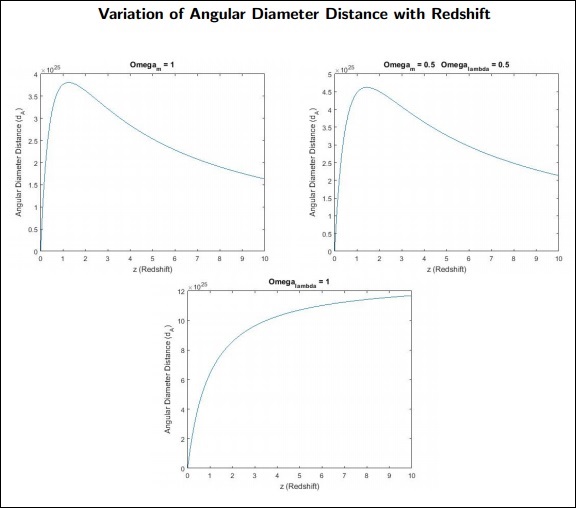
Punti da ricordare
Se conosciamo la dimensione di una sorgente, la sua larghezza angolare ci dirà la sua distanza dall'osservatore.
La distanza corretta è la distanza percorsa dai fotoni dalla sorgente a noi.
La distanza in movimento è la distanza tra gli oggetti in uno spazio che non si espande.