Cosmologia - Guida rapida
Cosmologyè lo studio dell'universo. Risalendo indietro nel tempo, c'erano diverse scuole di pensiero sull'origine dell'universo. Molti studiosi hanno creduto nelSteady State Theory. Secondo questa teoria, l'universo era sempre lo stesso, non aveva inizio.
Mentre c'era un gruppo di persone che avevano fede nel Big Bang Theory. Questa teoria prevede l'inizio dell'universo. C'erano prove di radiazioni calde escluse dal Big Bang, che ancora una volta supporta il modello. La teoria del Big Bang prevede l'abbondanza di elementi luminosi nell'universo. Quindi, seguendo il famoso modello del Big Bang, possiamo affermare che l'universo ha avuto un inizio. Viviamo in un universo in espansione.
Il Redshift di Hubble
All'inizio del 1900, il telescopio all'avanguardia, Mt Wilson, un telescopio da 100 pollici, era il più grande telescopio allora. Hubble è stato uno degli scienziati di spicco, che ha lavorato con quel telescopio. Ha scoperto che c'erano galassie fuori dalla Via Lattea.Extragalactic Astronomyha solo 100 anni. Il monte Wilson era il più grande telescopio fino a quando non fu costruito il Palmer Observatory che aveva un telescopio da 200 pollici.
HubbleHumason non era l'unica persona che osservava le galassie al di fuori della Via Lattea, lo aiutò. Hanno iniziato a misurare gli spettri delle galassie vicine. Hanno quindi osservato che uno spettro galattico era nella gamma di lunghezze d'onda visibili con emissione continua. C'erano linee di emissione e assorbimento in cima al continuum. Da queste linee possiamo stimare se la galassia si sta allontanando da noi o verso di noi.
Quando otteniamo uno spettro, supponiamo che provenga la linea più forte H-α. Dalla letteratura, la linea più forte dovrebbe apparire in6563 Å, ma se la linea si verifica da qualche parte 7000Å, possiamo facilmente dire che è spostato verso il rosso.
Dal Special Theory of Relativity,
$$ 1 + z = \ sqrt {\ frac {1+ \ frac {v} {c}} {1- \ frac {v} {c}}} $$
dove, Z è il redshift, un numero adimensionale ev è la velocità di recessione.
$$ \ frac {\ lambda_ {obs}} {\ lambda_ {rest}} = 1 + z $$
Hubble e Humason si sono elencati 22 Galaxiesnella loro carta. Quasi tutte queste galassie hanno mostrato spostamento verso il rosso. Hanno tracciato la velocità (km / s) rispetto alla distanza (Mpc). Hanno osservato una tendenza lineare e Hubble ha presentato la sua famosa legge come segue.
$$ v_r = H_o d $$
Questo è il Hubble Redshift Distance Relationship. Il pedicerindica che l'espansione è in direzione radiale. Mentre $ v_r $ è la velocità di recessione, $ H_o $ è il parametro di Hubble,dè la distanza della galassia da noi. Hanno concluso che le galassie lontane si ritirano più velocemente da noi, se il tasso di espansione dell'universo è uniforme.
L'espansione
Tutto si sta allontanando da noi. Le galassie non sono stazionarie, c'è sempre qualche espansione armonica. Le unità del parametro Hubble sono km sec −1 Mpc −1 . Se uno esce a una distanza di - 1 Mpc, le galassie si muovono alla velocità di 200 km / sec. Il parametro Hubble ci fornisce la velocità di espansione. Come per Hubble e Humason, il valore di $ H_o $ è 200 km / sec / Mpc.
I dati hanno mostrato che tutte le galassie si stanno allontanando da noi. Quindi, è evidente che siamo al centro dell'universo. Ma Hubble non ha commesso questo errore, secondo lui, in qualunque galassia viviamo, troveremmo tutte le altre galassie che si allontanano da noi. Quindi, la conclusione è che lo spazio tra le galassie si espande e non c'è centro dell'universo.
L'espansione sta avvenendo ovunque. Tuttavia, ci sono alcune forze che si oppongono all'espansione. Legami chimici, forza gravitazionale e altre forze attrattive tengono insieme gli oggetti. In precedenza tutti gli oggetti erano vicini tra loro. Considerando il Big Bang come una forza impulsiva, questi oggetti sono destinati ad allontanarsi l'uno dall'altro.
Scala temporale
Su scala locale, la cinematica è governata dalla gravità. Nella legge di Hubble originale, c'erano alcune galassie che mostravano il blue shift. Questo può essere attribuito al potenziale gravitazionale combinato delle galassie. La gravità ha disaccoppiato le cose dalla legge di Hubble. La Galassia di Andromeda sta venendo verso di noi. La gravità sta cercando di rallentare le cose. Inizialmente l'espansione stava rallentando, ora sta accelerando.
C'era un Cosmic JerkA causa di ciò. Sono state effettuate diverse stime del parametro Hubble. Si è evoluto negli ultimi 90 anni da 500 km / sec / Mpc a 69 km / sec / Mpc. La disparità nel valore era dovuta alla sottostima della distanza. IlCepheid Stars sono stati usati come calibratori di distanza, tuttavia esistono diversi tipi di stelle Cefeidi e questo fatto non è stato considerato per la stima del parametro di Hubble.
Ora di Hubble
La costante di Hubble ci fornisce una stima realistica dell'età dell'universo. $ H_o $ darebbe l'età dell'universo a condizione che le galassie si muovano con la stessa velocità. L'inverso di $ H_o $ ci dà il tempo di Hubble.
$$ t_H = \ frac {1} {H_o} $$
Sostituendo il valore attuale di $ H_o, t_H $ = 14miliardi di anni. La velocità di espansione è stata costante durante l'inizio dell'Universo. Anche se questo non è vero, $ H_o $ fornisce un limite utile all'età dell'universo. Assumendo un tasso di espansione costante, quando tracciamo un grafico tra distanza e tempo, la pendenza del grafico è data dalla velocità.
In questo caso, il tempo di Hubble è uguale al tempo effettivo. Tuttavia, se l'universo si fosse espanso più velocemente in passato e più lentamente nel presente, il tempo di Hubble fornisce un limite massimo di età dell'universo. Se l'universo si stava espandendo lentamente prima e accelera ora, allora il tempo di Hubble darà un limite inferiore all'età dell'universo.
$ t_H = t_ {età} $ - se il tasso di espansione è costante.
$ t_H> t_ {age} $ - se l'universo si è espanso più velocemente in passato e più lentamente nel presente.
$ t_H <t_ {age} $ - se l'universo si è espanso più lentamente in passato e più velocemente nel presente.
Considera un gruppo di 10 galassie che si trovano a 200 Mpc da un altro gruppo di galassie. Le galassie all'interno di un ammasso non concludono mai che l'universo si sta espandendo perché la cinematica all'interno di un gruppo locale è governata dalla gravitazione.
Punti da ricordare
La cosmologia è lo studio del passato, presente e futuro del nostro universo.
Il nostro universo ha circa 14 miliardi di anni.
L'universo è in continua espansione.
Il parametro Hubble è una misura dell'età dell'universo.
Valore corrente di Ho è 69 km / sec / Mpc.
Per molto tempo nessuno ha considerato le galassie presenti al di fuori della nostra Via Lattea. Nel 1924, Edwin Hubble lo scoprìCepheid’snella Nebulosa di Andromeda e ha stimato la loro distanza. Ha concluso che queste "Nebulose Spirali" erano in realtà altre galassie e non una parte della nostra Via Lattea. Quindi, ha stabilito che M31 (Galassia di Andromeda) è un universo insulare. Questa è stata la nascita diExtragalactic Astronomy.
Lo spettacolo di Cefeide a periodic dip in their brightness. Le osservazioni mostrano che il periodo tra cali successivi chiamato periodo delle pulsazioni è correlato alla luminosità. Quindi, possono essere usati come indicatori di distanza. Le stelle della sequenza principale come il Sole sono in equilibrio idrostatico e bruciano idrogeno nel loro nucleo. Dopo che l'idrogeno è completamente bruciato, le stelle si muovono verso la fase della Gigante Rossa e cercano di ritrovare il loro equilibrio.
Le Cepheid Stars sono stelle post Main Sequence che transitano dalle stelle Main Sequence ai Giganti Rossi.
Classificazione delle Cefeidi
Esistono 3 ampie classi di queste stelle variabili pulsanti:
Type-I Cepheids (o Cefeidi Classiche) - periodo di 30-100 giorni.
Type-II Cepheids (o W Virginis Stars) - periodo di 1-50 giorni.
RR Lyrae Stars - periodo di 0,1-1 giorno.
A quel tempo, Hubble non era a conoscenza di questa classificazione delle stelle variabili. Ecco perché c'era una sovrastima della costante di Hubble, a causa della quale stimava un'età inferiore del nostro universo. Quindi, anche la velocità di recessione è stata sovrastimata. In Cefeide, i disturbi si propagano radialmente verso l'esterno dal centro della stella fino a raggiungere il nuovo equilibrio.
Relazione tra luminosità e periodo di pulsazione
Cerchiamo ora di capire le basi fisiche del fatto che un periodo di pulsazione più alto implica più luminosità. Considera una stella di luminosità L e massa M.
Sappiamo che -
$$ L \ propto M ^ \ alpha $$
dove α = da 3 a 4 per stelle di piccola massa.
Dal Stefan Boltzmann Law, sappiamo che -
$$ L \ propto R ^ 2 T ^ 4 $$
Se R è il raggio e $ c_s $ è la velocità del suono, quindi il periodo della pulsazione P può essere scritto come -
$$ P = R / c_s $$
Ma la velocità del suono attraverso qualsiasi mezzo può essere espressa in termini di temperatura come:
$$ c_s = \ sqrt {\ frac {\ gamma P} {\ rho}} $$
Qui, γ è 1 per i casi isotermici.
Per un gas ideale, P = nkT, dove k è il Boltzmann Constant. Quindi, possiamo scrivere -
$$ P = \ frac {\ rho kT} {m} $$
dove $ \ rho $ è la densità e m è la massa di un protone.
Pertanto, il periodo è dato da -
$$ P \ cong \ frac {Rm ^ {\ frac {1} {2}}} {(kT) ^ {{\ frac {1} {2}}}} $$
Virial Theorem afferma che per una distribuzione stabile, auto gravitante e sferica di oggetti di uguale massa (come stelle, galassie), l'energia cinetica totale k dell'oggetto è uguale a meno metà dell'energia potenziale gravitazionale totale u, cioè
$$ u = -2k $$
Supponiamo che il teorema viriale valga per queste stelle variabili. Se consideriamo un protone proprio sulla superficie della stella, allora dal teorema viriale possiamo dire:
$$ \ frac {GMm} {R} = mv ^ 2 $$
Dalla distribuzione Maxwell,
$$ v = \ sqrt {\ frac {3kT} {2}} $$
Pertanto, punto -
$$ P \ sim \ frac {RR ^ {\ frac {1} {2}}} {(GM) ^ {\ frac {1} {2}}} $$
il che implica
$$ P \ propto \ frac {R ^ {\ frac {3} {2}}} {M ^ {\ frac {1} {2}}} $$
Sappiamo che - $ M \ propto L ^ {1 / \ alpha} $
Anche $ R \ propto L ^ {1/2} $
Così per β > 0, finalmente otteniamo - $ P \ propto L ^ \ beta $
Punti da ricordare
Le Cepheid Stars sono stelle post Main Sequence che stanno transitando dalle stelle Main Sequence ai Red Giants.
Le Cefeidi sono di 3 tipi: Tipo-I, Tipo-II, RR-Lyrae in ordine decrescente di periodo pulsante.
Il periodo pulsante di Cefeide è direttamente proporzionale alla sua luminosità (luminosità).
Le osservazioni di Hubble hanno utilizzato il fatto che la velocità radiale è correlata allo spostamento del Spectral Lines. Qui, osserveremo quattro casi e troveremo una relazione tra Recessional Velocity ($ v_r $) e Red Shift (z).
Caso 1: caso non relativistico di spostamento della sorgente
In questo caso, v è molto inferiore a c. La sorgente emette un segnale (suono, luce, ecc.), Che si propaga comeWavefronts. L'intervallo di tempo tra l'invio di due segnali consecutivi nel frame sorgente èΔts. L'intervallo di tempo tra la ricezione di due segnali consecutivi nel frame dell'osservatore èΔto.

Se sia l'osservatore che la sorgente sono stazionari, allora Δts = Δto, ma questo non è il caso qui. Invece, la relazione è la seguente.
$$ \ Delta t_o = \ Delta t_s + \ frac {\ Delta l} {c} $$
Ora $ \ Delta l = v \ Delta t_s $
Inoltre, poiché (velocità dell'onda x tempo) = lunghezza d'onda, otteniamo
$$ \ frac {\ Delta t_o} {\ Delta t_s} = \ frac {\ lambda_o} {\ lambda_s} $$
Dalle equazioni precedenti, otteniamo la seguente relazione:
$$ \ frac {\ lambda_o} {\ lambda_s} = 1 + \ frac {v} {c} $$
dove $ \ lambda _s $ è la lunghezza d'onda del segnale alla sorgente e $ \ lambda _o $ è la lunghezza d'onda del segnale come interpretata dall'osservatore.
Qui, poiché la sorgente si sta allontanando dall'osservatore, v è positivo.
Spostamento rosso -
$$ z = \ frac {\ lambda_o - \ lambda_s} {\ lambda_s} = \ frac {\ lambda_o} {\ lambda_s} - 1 $$
Dalle equazioni precedenti, otteniamo lo spostamento rosso come segue.
$$ z = \ frac {v} {c} $$
Caso 2: caso non relativistico di movimento di osservatori
In questo caso, v è molto inferiore a c. Qui $ \ Delta l $ è diverso.
$$ \ Delta l = v \ Delta t_o $$

Sulla semplificazione, otteniamo:
$$ \ frac {\ Delta t_o} {\ Delta t_s} = \ left (1 - \ frac {v} {c} \ right) ^ {- 1} $$
Otteniamo lo spostamento rosso come segue:
$$ z = \ frac {v / c} {1-v / c} $$
Da v << c, l'espressione di spostamento verso il rosso sia per il caso I che per il caso II è approssimativamente la stessa.
Vediamo come differiscono gli spostamenti verso il rosso ottenuti nei due casi precedenti.
$$ z_ {II} - z_I = \ frac {v} {c} \ left [\ frac {1} {1 - v / c} -1 \ right] $$
Quindi, $ z_ {II} - z_ {I} $ è un numero molto piccolo a causa del fattore $ (v / c) ^ 2 $.
Ciò implica che, se v << c, non possiamo dire se la sorgente si sta muovendo o se l'osservatore si sta muovendo.
Vediamo ora di capire il Basics of STR (Teoria della Relatività Speciale) -
La velocità della luce è una costante.
Quando la sorgente (o l'osservatore) si muove a una velocità paragonabile a quella della luce, si osservano effetti relativistici.
Dilatazione temporale: $ \ Delta t_o = \ gamma \ Delta t_s $
Contrazione della lunghezza: $ \ Delta l_o = \ Delta t_s / \ gamma $
Qui $ \ gamma $ è il file Lorrentz factor, maggiore di 1.
$$ \ gamma = \ frac {1} {\ sqrt {1- (v ^ 2 / c ^ 2)}} $$
Caso 3: caso relativistico di spostamento della sorgente
In questo caso, v è paragonabile a c. Fare riferimento alla stessa figura del caso I. A causa dell'effetto relativistico, si osserva la dilatazione del tempo e quindi si ottiene la seguente relazione. (La fonte si sta muovendo con velocità relativistica)
$$ \ Delta t_o = \ gamma \ Delta t_s + \ frac {\ Delta l} {c} $$
$$ \ Delta l = \ frac {v \ gamma \ Delta t_s} {c} $$
$$ \ frac {\ Delta t_o} {\ Delta t_s} = \ frac {1 + v / c} {\ sqrt {1- (v ^ 2 / c ^ 2)}} $$
Con un'ulteriore semplificazione, otteniamo,
$$ 1 + z = \ sqrt {\ frac {1 + v / c} {1-v / c}} $$
L'espressione sopra è nota come Kinematic Doppler Shift Expression.
Caso 4: caso relativistico del movimento di un osservatore
Fare riferimento alla stessa figura del caso II. A causa dell'effetto relativistico, si osserva un accorciamento del tempo e quindi si ottiene la seguente relazione. (L'osservatore si sta muovendo con velocità relativistica)
$$ \ Delta t_o = \ frac {\ Delta t_s} {\ gamma} + \ frac {\ Delta l} {c} $$
$$ \ Delta l = \ frac {v \ Delta t_o} {c} $$
$$ \ frac {\ Delta t_o} {\ Delta t_s} = \ frac {\ sqrt {1- (v ^ 2 / c ^ 2)}} {1-v / c} $$
Con un'ulteriore semplificazione, otteniamo:
$$ 1 + z = \ sqrt {\ frac {1+ v / c} {1- v / c}} $$
L'espressione sopra è la stessa che abbiamo ottenuto per il Caso III.
Punti da ricordare
La velocità di recessione e il redshift di una stella sono quantità correlate.
In un caso non relativistico, non possiamo determinare se la sorgente è in movimento o stazionaria.
In un caso relativistico, non c'è differenza nella relazione velocità di spostamento verso il rosso-recessione per il movimento della sorgente o dell'osservatore.
Gli orologi in movimento si muovono più lentamente, è un risultato diretto della teoria della relatività.
Una galassia in redshift z = 10, corrisponde a v≈80% di c. La massa della Via Lattea è intorno1011M⊙, se consideriamo la materia oscura, lo è 1012M⊙. La nostra via lattea è quindi enorme. Se si muove all'80% dic, non si adatta al concetto generale di come si muovono gli oggetti.
Sappiamo,
$$ \ frac {v_r} {c} = \ frac {\ lambda_ {obs} - \ lambda {rest}} {\ lambda_ {rest}} $$
Per piccoli valori di z,
$$ z = \ frac {v_r} {c} = \ frac {\ lambda_ {obs} - \ lambda_ {rest}} {\ lambda_ {rest}} $$
Nel grafico seguente, la classe tra flusso e lunghezza d'onda, ci sono linee di emissione in cima al continuo. DalH-α informazioni sulla riga, arriviamo a concludere che grosso modo z = 7. Ciò significa che la galassia si sta muovendo al 70% dic. Stiamo osservando uno spostamento e interpretandolo come velocità. Dovremmo sbarazzarci di questa nozione e guardarezin un altro modo. Immagina lo spazio come una griglia 2D che rappresenta l'universo come mostrato di seguito.

Considera la stella nera come la nostra via lattea e la stella blu come un'altra galassia. Quando registriamo la luce da questa galassia, vediamo lo spettro e scopriamo il suo spostamento verso il rosso, cioè la galassia si sta allontanando. Quando il fotone è stato emesso, aveva velocità relativa.
E se lo spazio si stesse espandendo?
È un redshift istantaneo del fotone. Gli spostamenti cumulativi verso il rosso lungo lo spazio tra due galassie tenderanno ad un ampio spostamento verso il rosso. La lunghezza d'onda cambierà finalmente. È l'espansione dello spazio piuttosto che il movimento cinematico delle galassie.
L'immagine seguente mostra se la gravità reciproca supera l'espansione, allora questo non partecipa alla legge di Hubble.

Nel Kinematic Doppler Shift, il redshift è indotto in un fotone al momento dell'emissione. In un spostamento verso il rosso cosmologico, in ogni fase, viene spostato verso il rosso cumulativamente. In un potenziale gravitazionale, un fotone diventerà blu spostato. Man mano che esce dal potenziale gravitazionale, viene spostato verso il rosso.
Secondo una teoria della relatività speciale, due oggetti che passano l'uno accanto all'altro non possono avere una velocità relativa maggiore della velocità della luce. La velocità di cui parliamo è dell'espansione dell'universo. Per valori elevati di z, il redshift è cosmologico e non è una misura valida dell'effettiva velocità di recessione dell'oggetto rispetto a noi.
Il principio cosmologico
Deriva dal Copernicus Notiondell'universo. Secondo questa nozione, l'universo è omogeneo e isotropo. Non esiste una direzione e una posizione preferite nell'universo.
L'omogeneità significa che indipendentemente dalla parte dell'universo in cui risiedi, vedrai che l'universo è lo stesso in tutte le parti. La natura isotropa significa che, indipendentemente dalla direzione in cui guardi, vedrai la stessa struttura.
Un esempio calzante di omogeneità è un campo di risaia. Sembra omogeneo da tutte le parti, ma quando scorre il vento, ci sono variazioni nel suo orientamento, quindi non è isotropo. Considera una montagna su un terreno pianeggiante e un osservatore è in piedi sulla cima della montagna. Vedrà la natura isotropa del terreno pianeggiante, ma non è omogeneo. Se in un universo omogeneo, è isotropo in un punto, è isotropo ovunque.
Sono state effettuate indagini su larga scala per mappare l'universo. Sloan Digital Sky Surveyè una di queste indagini, che non si è concentrata molto sulla declinazione, ma sull'ascensione retta. Il tempo di ricerca è di circa 2 miliardi di anni. Ogni pixel corrisponde alla posizione di una galassia e il colore corrisponde alla struttura morfologica. Il colore verde rappresentava la galassia a spirale blu mentre il falso colore rosso indicava galassie massicce.
Le galassie sono presenti in una struttura filamentosa in una rete cosmologica e ci sono dei vuoti tra le galassie.
$ \ delta M / M \ cong 1 $ cioè, la fluttuazione della distribuzione di massa è 1 M è la massa della materia presente all'interno di un dato cubo. In questo caso, prendi il cubo del volume da 50 Mpc.
Per un lato cubo di 1000 Mpc, $ \ delta M / M \ cong 10 ^ {- 4} $.
Un modo per quantificare l'omogeneità è prendere le fluttuazioni di massa. Le fluttuazioni di massa saranno maggiori a scale inferiori.
Per quantificare la natura isotropa, si consideri la radiazione di fondo cosmica a microonde. L'universo è quasi isotropo a grandi scale angolari.
Punti da ricordare
Due oggetti che passano l'uno accanto all'altro non possono avere una velocità relativa maggiore della velocità della luce.
Il principio cosmologico afferma che l'universo è omogeneo e isotropo.
Questa omogeneità esiste su una scala angolare molto ampia e non su scale minori.
SDSS (Sloan Digital Sky Survey) è uno sforzo per mappare il cielo notturno, verificando il principio cosmologico.
Secondo la legge di conservazione dell'energia e la legge di conservazione della massa, la quantità totale di energia inclusa la massa (E = mc 2 ) rimane invariata in ogni fase di qualsiasi processo nell'universo. L'espansione dell'universo stesso consuma energia che può derivare dallo stiramento della lunghezza d'onda dei fotoni (Cosmological Redshift), dalle interazioni di energia oscura, ecc.
Per accelerare il rilevamento di oltre 26.000 galassie, Stephen A. Shectmanha progettato uno strumento in grado di misurare 112 galassie contemporaneamente. In una piastra metallica sono stati praticati dei fori che corrispondevano alle posizioni delle galassie nel cielo. I cavi in fibra ottica trasportavano la luce da ciascuna galassia fino a un canale separato su uno spettrografo al telescopio du Pont di 2,5 metri alCarnegie Observatories sul Cerro Las Campanas in Cile.
Per la massima efficienza, una tecnica specializzata nota come Drift-Scan Photometryè stato utilizzato, in cui il telescopio è stato puntato all'inizio di un campo di rilevamento e quindi l'azionamento automatico è stato spento. Il telescopio rimase immobile mentre il cielo scivolava via. I computer leggono le informazioni dal fileCCD Detectoralla stessa velocità della rotazione terrestre, producendo un'immagine lunga e continua a una latitudine celeste costante. Il completamento della fotometria ha richiesto un totale di 450 ore.
Esistono diverse forme di rumore e la loro modellazione matematica è diversa a seconda delle sue proprietà. Vari processi fisici evolvono lo spettro di potenza dell'universo su larga scala. Lo spettro di potenza iniziale impartito a causa delle fluttuazioni quantistiche segue una terza potenza di frequenza negativa che è una forma diPink Noise Spectrum in tre dimensioni.
La metrica
In cosmologia, bisogna prima avere una definizione di spazio. Una metrica è un'espressione matematica che descrive punti nello spazio. L'osservazione del cielo avviene in una geometria sferica; quindi deve essere utilizzato un sistema di coordinate sferiche. La distanza tra due punti ravvicinati è data da:
$$ ds ^ 2 = dr ^ 2 + r ^ 2 \ theta ^ 2 + r ^ 2 sin ^ 2 \ theta d \ phi ^ 2 $$
L'immagine seguente mostra la geometria nello spazio euclideo tridimensionale non in espansione.

Questa geometria è ancora nello spazio euclideo tridimensionale non in espansione. Quindi, la griglia di riferimento che definisce il frame stesso si espanderebbe. L'immagine seguente mostra la metrica aumentata.

Un fattore di scala viene inserito nell'equazione dello spazio non in espansione, chiamato "fattore di scala" che incorpora l'espansione dell'universo rispetto al tempo.
$$ ds ^ 2 = a ^ 2 (t) \ sinistra [dr ^ 2 + r ^ 2 \ theta ^ 2 + r ^ 2 sin ^ 2 \ theta d \ phi ^ 2 \ right] $$
dove a(t) è il fattore di scala, a volte scritto come R(t). Mentre,a(t) > 1 significa ingrandimento della metrica, mentre a(t) < 1 significa restringimento della metrica e a(t) = 1significa metrica costante. Come convenzione,a(t0) = 1.
Comoving Coordinate System
In un Comoving Coordinate System, la scala di misurazione si espande insieme alla cornice (universo in espansione).
Qui, $ \ left [dr ^ 2 + r ^ 2 \ theta ^ 2 + r ^ 2 sin ^ 2 \ theta d \ phi ^ 2 \ right] $ è la distanza di spostamento, e $ ds ^ 2 $ è la Distanza corretta.
La distanza corretta corrisponderà alla distanza effettiva misurata da una galassia lontana dalla terra al momento dell'osservazione, ovvero la distanza istantanea degli oggetti.
Questo perché la distanza percorsa da un fotone quando raggiunge l'osservatore da una sorgente distante sarà quella ricevuta a $ t = t_0 $ dell'osservatore, il che significherebbe che la distanza istantanea osservata sarà la distanza corretta, e si può prevedere le distanze future utilizzando il fattore di velocità e la lunghezza misurata iniziale come riferimento.
Il concetto di Comoving e distanza appropriata è importante per misurare il valore effettivo della densità numerica delle galassie nel volume dato dello spazio osservato. Si deve usare la distanza di Comoving per calcolare la densità al momento della loro formazione quando il fotone osservato è stato emesso. Ciò può essere ottenuto una volta stimato il tasso di espansione dell'universo.
Per stimare il tasso di espansione, si può osservare il cambiamento nella distanza di una galassia distante osservata per un lungo periodo di tempo.
Punti da ricordare
Una metrica è un'espressione matematica che descrive i punti nello spazio.
Il fattore di scala determina se l'universo si contrae o si espande.
In un sistema di coordinate mobile, la scala di misurazione si espande insieme alla cornice (universo in espansione).
La distanza corretta è la distanza istantanea degli oggetti.
La distanza di spostamento è la distanza effettiva degli oggetti.
In questo capitolo, comprenderemo in dettaglio la metrica di Robertson-Walker.
Modello per il fattore di scala che cambia nel tempo
Supponiamo che un fotone venga emesso da una galassia lontana. Lo spazio è in avanti per il fotone in tutte le direzioni. L'espansione dell'universo è in tutte le direzioni. Vediamo come cambia il fattore di scala nel tempo nei seguenti passaggi.
Step 1 - Per un universo statico, il fattore di scala è 1, ovvero il valore della distanza di spostamento è la distanza tra gli oggetti.
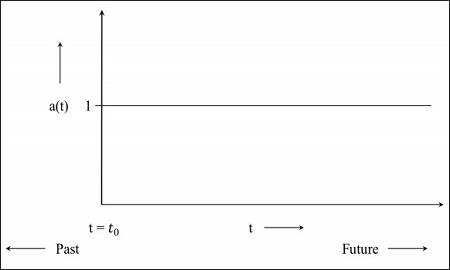
Step 2- L'immagine seguente è il grafico dell'universo che è ancora in espansione ma a una velocità decrescente, il che significa che il grafico inizierà nel passato. Ilt = 0 indica che l'universo è iniziato da quel punto.

Step 3 - L'immagine seguente è il grafico dell'universo che si espande a una velocità maggiore.

Step 4 - L'immagine seguente è il grafico per l'universo che inizia a contrarsi da adesso.

Se il valore del fattore di scala diventa 0 durante la contrazione dell'universo, implica che la distanza tra gli oggetti diventa 0, cioè la distanza corretta diventa 0. La distanza mobile che è la distanza tra gli oggetti in un universo presente, è una quantità costante. In futuro, quando il fattore di scala diventerà0, tutto si avvicinerà. Il modello dipende dal componente dell'universo.
La metrica per l'universo in espansione piatto (euclideo: non vi è alcun parametro per la curvatura) è data come -
$$ ds ^ 2 = a ^ 2 (t) \ sinistra (dr ^ 2 + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2 \ destra) $$
Per lo spazio-tempo, l'elemento linea che abbiamo ottenuto nell'equazione precedente viene modificato come -
$$ ds ^ 2 = c ^ 2dt ^ 2 - \ sinistra \ {a ^ 2 (t) \ sinistra (dr ^ 2 + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2 \ destra) \ destra \} $$
Per lo spazio-tempo, il tempo in cui il fotone viene emesso e quello in cui viene rilevato è diverso. La distanza corretta è la distanza istantanea dagli oggetti che può cambiare nel tempo a causa dell'espansione dell'universo. È la distanza percorsa dal fotone da diversi oggetti per arrivare a noi. È correlato alla distanza comovente come -
$$ d_p = a (t) \ times d_c $$
dove $ d_p $ è la distanza corretta e $ d_c $ è la distanza di spostamento, che è fissa.
La distanza misurata dagli oggetti nell'universo attuale è considerata come distanza in movimento, il che significa che la distanza in movimento è fissa e non viene modificata dall'espansione. In passato, il fattore di scala era inferiore a 1, il che indica che la distanza corretta era inferiore.
Possiamo misurare il redshift in una galassia. Quindi la giusta distanza $ d_p $ corrisponde a $ c \ volte t (z) $, dove $ t (z) $ è il tempo di ricerca verso un redshift ec è la velocità della luce nel vuoto. Il tempo di ricerca è una funzione del redshift(z).
Sulla base della nozione di cui sopra, analizziamo come viene interpretato lo spostamento verso il rosso cosmologico in questo scenario di $ d_p = a (t) \ times d_c $.
Supponiamo che un fotone (che è legato alla terra) sia emesso dalla galassia, G. $ t_ {em} $ corrisponde al momento in cui è stato emesso il fotone; $ a (t_ {em}) $ era il fattore di scala in quel momento in cui il fotone veniva emesso. Al momento del rilevamento del fotone, l'intero universo si era espanso, ovvero il fotone è spostato verso il rosso al momento del rilevamento. $ T_ {obs} $ corrisponde al momento in cui viene rilevato il fotone e il fattore di scala corrispondente è $ a (t_ {obs}) $.
Il fattore per cui l'universo è cresciuto è dato da:
$$ \ frac {a (t_ {obs})} {a (t_ {em})} $$
Il fattore di espansione della lunghezza d'onda è:
$$ \ frac {\ lambda_ {obs}} {\ lambda_ {em}} $$
che è uguale al fattore di crescita dell'universo. I simboli hanno il loro significato abituale. Perciò,
$$ \ frac {a (t_ {obs})} {a (t_ {em})} = \ frac {\ lambda_ {obs}} {\ lambda_ {em}} $$
Conosciamo quel redshift (z) è -
$$ z = \ frac {\ lambda_ {obs} - \ lambda_ {em}} {\ lambda_ {em}} = \ frac {\ lambda_ {obs}} {\ lambda_ {em}} - 1 $$
$$ 1 + z = \ frac {a (t_ {obs})} {a (t_ {em})} $$
Il valore attuale del fattore di scala è 1, quindi $ a (t_ {obs}) = 1 $ e denota il fattore di scala quando il fotone è stato emesso in passato da $ a (t) $.
Perciò,
$$ 1 + z = \ frac {1} {a (t)} $$
Interpretazione del Redshift in cosmologia
Per capirlo, prendiamo il seguente esempio: Se $ z = 2 $ allora $ a (t) = 1/3 $.
Implica che l'universo si sia espanso di un fattore tre da quando la luce ha lasciato quell'oggetto. La lunghezza d'onda della radiazione ricevuta si è espansa di un fattore tre perché lo spazio si è espanso dello stesso fattore durante il suo transito dall'oggetto emittente. Va notato che a valori così grandi diz, il redshift è principalmente il redshift cosmologico e non è una misura valida dell'effettiva velocità di recessione dell'oggetto rispetto a noi.
Per il fondo cosmico a microonde (CMB), z = 1089, il che significa che l'universo attuale si è espanso di un fattore ∼1090. La metrica per l'universo piatto, euclideo, in espansione è data come:
$$ ds ^ 2 = a ^ 2 (t) (dr ^ 2 + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2) $$
Vogliamo scrivere la metrica in qualsiasi curvatura.
Robertson and Walker provato per qualsiasi universo di curvatura (che è omogeneo e isotropo), la metrica è data come -
$$ ds ^ 2 = a ^ 2 (t) \ sinistra [\ frac {dr ^ 2} {1-kr ^ 2} + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2 \ right] $$
Questo è generalmente noto come Robertson–Walker Metriced è vero per qualsiasi topologia dello spazio. Si prega di notare il fattore aggiuntivo in $ dr ^ 2 $. Qui è la costante di curvatura.
Geometria dell'Universo
La Geometria dell'Universo è spiegata con l'aiuto delle seguenti Curvature, che includono:
- Curvatura positiva
- Curvatura negativa
- Curvatura zero
Cerchiamo di capire ciascuno di questi in dettaglio.
Curvatura positiva
Se un piano tangente disegnato in un punto qualsiasi della superficie della curvatura non si interseca in alcun punto della superficie, si parla di superficie con una curvatura positiva, cioè la superficie rimane su un lato del piano tangente in quel punto. La superficie della sfera ha una curvatura positiva.
Curvatura negativa
Se un piano tangente disegnato in un punto sulla superficie della curvatura si interseca in un punto qualsiasi della superficie, viene chiamato come una superficie con una curvatura negativa, cioè la superficie si curva lontano dal piano tangente in due direzioni diverse. Una superficie a forma di sella ha una curvatura negativa.
Considera ora la superficie di una sfera. Se un triangolo è costruito sulla superficie della sfera unendo tre punti con geodetica (arco di grandi cerchi), la somma degli angoli interni del triangolo sferico è maggiore di 180 o , cioè -
$$ \ alpha + \ beta + \ gamma> \ pi $$
Tali spazi sono chiamati spazi curvi positivamente. Inoltre, la curvatura è omogenea e isotropa. In generale, l'angolo ai vertici del triangolo sferico segue la relazione -
$$ \ alpha + \ beta + \ gamma = \ pi + A / R ^ 2 $$
dove A è l'area del triangolo e Rè il raggio della sfera. L'immagine seguente mostra uno spazio curvo positivamente.

Per una curvatura positiva, le linee parallele dovrebbero incontrarsi. Considera la superficie della terra, che è uno spazio positivamente curvo. Prendi due punti di partenza sull'equatore. Le linee che attraversano l'equatore ad angolo retto sono note come linee di longitudine. Poiché queste linee attraversano l'equatore ad angolo retto, possono essere indicate come linee parallele. Partendo dall'equatore, alla fine si intersecano ai poli. Questo metodo è stato utilizzato daCarl Gauss e altri per comprendere la topologia della terra.
Considera uno spazio curvo negativamente (una sella mostrata nell'immagine seguente), la somma degli angoli interni del triangolo è inferiore a 180 o , cioè -
$$ \ alpha + \ beta + \ gamma <\ pi $$
L'angolo ai vertici segue la relazione -
$$ \ alpha + \ beta + \ gamma = \ pi - A / R ^ 2 $$

Curvatura zero
Una superficie piana ha curvatura zero. Ora per uno spazio piatto, se si prende un piano e si costruisce un triangolo unendo tre punti con geodetiche (linee rette), la somma interna degli angoli sarà -
$$ \ alpha + \ beta + \ gamma = \ pi $$
L'immagine seguente è uno spazio bidimensionale piatto.

Se si vuole che uno spazio sia omogeneo e isotropo, rimangono solo tre possibilità: lo spazio può essere uniformemente piatto oppure può avere una curvatura positiva uniforme oppure può avere una curvatura negativa uniforme.
La costante di curvatura può assumere uno dei seguenti tre valori.
$$ k = \ begin {case} +1, & for \: a \: positively \: curve \: space; \\\ quad 0, & for \: a \: flat \: space; \\ - 1, & per \: a \: negative \: curve \: space; \ end {case} $$
Topologia globale dell'universo
L'universo ha una certa topologia, ma localmente può avere rughe. A seconda di come la materia è distribuita nello spazio, ci sono variazioni minori nella curvatura. Supponiamo che esista una classe di oggetti che hanno la stessa dimensione reale indipendentemente da dove si trovi nell'universo, il che significa che sono come candele standard. Non hanno la stessa luminosità, ma hanno le stesse dimensioni.
Se l'oggetto si trova nello spazio curvo positivamente ei fotoni provengono dal punto A (un'estremità dell'oggetto) e B (altra estremità dell'oggetto), i fotoni si propagheranno parallelamente nello spazio curvo positivamente attraverso il percorso della geodetica e alla fine si incontreranno . Per un osservatore in C, sembrerà che provenga da due punti diversi in direzioni diverse.
Se l'oggetto si trova nell'universo locale e misuriamo la dimensione angolare, non è influenzato dalla curvatura. Se la stessa classe di oggetti viene vista con un redshift maggiore, la dimensione angolare non è correlata a.
$$ \ theta = \ frac {d} {r} $$
Dove d è la dimensione dell'oggetto e rè la distanza dall'oggetto, cioè se la dimensione è maggiore della dimensione locale, significa che la curvatura è positiva. L'immagine seguente è una rappresentazione del fotone rilevato in uno spazio curvo positivamente.

È da notare che non esiste un vero oggetto astrofisico di dimensioni e morfologia standard. Sebbene si pensasse che una massiccia galassia ellittica cD si adattasse alle candele standard, si è anche scoperto che si evolvono nel tempo.
Trovare le distanze dalle galassie
In questa sezione, discuteremo come trovare la distanza da una galassia prendendo in considerazione l'immagine seguente.

Considera la Via Lattea a (r, θ,) in una cornice di riposo cosmologico. Si può prendere = 0; (0, θ, ϕ), cioè il centro dell'universo invocando l'ipotesi di omogeneità.
Considera una galassia 'G' a (r1, θ,). La distanza (corretta) è la distanza radiale più breve percorsa da un fotone. Dalla simmetria spazio-tempo, la geodetica nulla da r = 0 a r = r1, ha una direzione costante nello spazio. Nella sua propagazione radiale, le coordinate angolari non cambiano. Se le coordinate angolari vengono modificate, non è il percorso più breve. Questo è il motivo per cui il termine curvatura è presente in dr 2 .
Punti da ricordare
L'espansione dell'universo è in tutte le direzioni.
L'universo può essere statico, in espansione o in contrazione a seconda dell'evoluzione del fattore di scala.
Le galassie CD si evolvono con il tempo e quindi non possono essere utilizzate come candele standard.
L'universo ha una certa topologia, ma localmente può avere rughe.
In questo capitolo, discuteremo del parametro Hubble e del fattore di scala.
Prerequisite - Redshift cosmologico, principi cosmologici.
Assumption - L'universo è omogeneo e isotropo.
Costante di Hubble con tasso frazionario di variazione del fattore di scala
In questa sezione metteremo in relazione la costante di Hubble con la velocità frazionaria del cambiamento del fattore di scala.
Possiamo scrivere la velocità nel modo seguente e semplificare.
$$ v = \ frac {\ mathrm {d} r_p} {\ mathrm {d} t} $$
$$ = \ frac {d [a (t) r_c} {dt} $$
$$ v = \ frac {\ mathrm {d} a} {\ mathrm {d} t} \ ast \ frac {1} {a} \ ast (ar_c) $$
$$ v = \ frac {\ mathrm {d} a} {\ mathrm {d} t} \ ast \ frac {1} {a} \ ast r_p $$
Qui, v è la velocità di recessione, a è il fattore di scala e rp è la giusta distanza tra le galassie.
Hubble’s Empirical Formula era della natura -
$$ v = H \ ast r_p $$
Quindi, confrontando le due equazioni precedenti otteniamo:
Hubble’s Parameter = Fractional rate of change of the scale factor
$$ H = da / dt \ ast 1 / a $$
Note- Questa non è una costante poiché il fattore di scala è una funzione del tempo. Quindi è chiamato parametro di Hubble e non costante di Hubble.
Empiricamente scriviamo -
$$ H = V / D $$
Quindi, da questa equazione, possiamo dedurlo da allora D è in aumento e V è una costante, quindi H si riduce con il tempo e l'espansione dell'universo.
Equazione di Friedmann in congiunzione con il modello di Robertson-Walker
In questa sezione, capiremo come viene utilizzata l'equazione di Friedmann in combinazione con il modello di Robertson-Walker. Per capirlo, prendiamo la seguente immagine che ha una massa di prova a distanzarp dal corpo di massa M come esempio.

Prendendo in considerazione l'immagine sopra, possiamo esprimere la forza come:
$$ F = G \ ast M \ ast \ frac {m} {r ^ 2_p} $$
Qui, G è la costante gravitazionale universale e ρ è la densità della materia all'interno dell'universo osservabile.
Ora, assumendo una densità di massa uniforme all'interno della sfera, possiamo scrivere:
$$ M = \ frac {4} {3} \ ast \ pi \ ast r_p ^ 3 \ ast \ rho $$
Usandoli nella nostra equazione della forza otteniamo:
$$ F = \ frac {4} {3} \ ast \ pi \ ast G \ ast r_p \ ast \ rho \ ast m $$
Quindi, possiamo scrivere l'energia potenziale e l'energia cinetica della massa m come -
$$ V = - \ frac {4} {3} \ ast \ pi \ ast G \ ast r ^ 2_p \ ast m \ ast \ rho $$
$$ KE = \ frac {1} {2} \ ast m \ ast \ frac {\ mathrm {d} r_p ^ 2} {\ mathrm {d} t} $$
Usando il Virial Theorem -
$$ U = KE + V $$
$$ U = \ frac {1} {2} \ ast m \ ast \ left (\ frac {\ mathrm {d} r_p} {\ mathrm {d} t} \ right) ^ 2 - \ frac {4} { 3} \ ast \ pi \ ast G \ ast r_p ^ 2 \ ast m \ ast \ rho $$
Ma qui, $ r_p = ar_c $. Quindi, otteniamo -
$$ U = \ frac {1} {2} \ ast m \ ast \ left (\ frac {\ mathrm {d} a} {\ mathrm {d} t} \ right) ^ 2 r_c ^ 2 - \ frac { 4} {3} \ ast \ pi \ ast G \ ast r_p ^ 2 \ ast m \ ast \ rho $$
Con un'ulteriore semplificazione, otteniamo l'equazione di Friedmann,
$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi} {3} \ ast G \ ast \ rho + \ frac {2U} {m} \ ast r_c ^ 2 \ ast a ^ 2 $$
Qui Uè una costante. Notiamo anche che l'universo in cui viviamo attualmente è dominato dalla materia, mentre la densità di energia della radiazione è molto bassa.
Punti da ricordare
Il parametro Hubble si riduce con il tempo e l'espansione dell'universo.
L'universo in cui viviamo attualmente è dominato dalla materia e la densità di energia della radiazione è molto bassa.
In questo capitolo capiremo cos'è l'equazione di Friedmann e studieremo in dettaglio i modelli del mondo per le diverse costanti di curvatura.
Equazione di Friedmann
Questa equazione ci parla dell'espansione dello spazio in modelli omogenei e isotropi dell'universo.
$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho + \ frac {2U} {mr_c ^ 2a ^ 2} $ $
Questo è stato modificato nel contesto di General Relativity (GR) e Robertson-Walker Metric come segue.
Utilizzando le equazioni GR -
$$ \ frac {2U} {mr_c ^ 2} = -kc ^ 2 $$
Dove kè la costante di curvatura. Perciò,
$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho - \ frac {kc ^ 2} {a ^ 2} $ $
Inoltre, $ \ rho $ viene sostituito dalla densità di energia che include materia, radiazione e qualsiasi altra forma di energia. Ma per scopi rappresentativi, è scritto come $ \ rho $.
Modelli del mondo per diverse costanti di curvatura
Vediamo ora le varie possibilità a seconda dei valori delle costanti di curvatura.
Caso 1: k = 1 o universo chiuso
Per un universo in espansione, $ da / dt> 0 $. Man mano che l'espansione continua, il primo termine sulla destra dell'equazione precedente diventa $ a ^ {- 3} $, mentre il secondo termine diventa $ a ^ {- 2} $. Quando i due termini diventano uguali l'universo arresta l'espansione. Quindi -
$$ \ frac {8 \ pi G} {3} \ rho = \ frac {kc ^ 2} {a ^ 2} $$
Qui, k = 1, quindi,
$$ a = \ left [\ frac {3c ^ 2} {8 \ pi G \ rho} \ right] ^ {\ frac {1} {2}} $$
Un tale universo è finito e ha un volume finito. Questo è chiamato universo chiuso.
Caso 2: k = -1 o Open Universe
Se k < 0, l'espansione non si fermerebbe mai. Dopo un certo punto, il primo termine sull'RHS può essere trascurato rispetto al secondo termine.
Qui, k = -1. Pertanto, $ da / dt ∼ c $.
In questo caso, l'universo sta procedendo per inerzia. Un tale universo ha spazio e tempo infiniti. Questo è chiamato universo aperto.
Caso 3: k = 0 o universo piatto
In questo caso, l'universo si sta espandendo a un ritmo decrescente. Qui, k = 0. Pertanto,
$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho $$
Un tale universo ha spazio e tempo infiniti. Questo è chiamato un universo piatto.
Punti da ricordare
L'equazione di Friedmann ci parla dell'espansione dello spazio in modelli omogenei e isotropi dell'universo.
A seconda dei diversi valori delle costanti di curvatura, possiamo avere un universo chiuso, aperto o piatto.
In questo capitolo, discuteremo l'equazione del fluido e come ci dice riguardo alla densità dell'universo che cambia nel tempo.
Stima di ρ c e ρ nell'universo presente
Per l'universo attuale -
$$ \ rho_c \ simeq 10 ^ {11} M_ \ odot M_ {pc} ^ {- 3} \ simeq 10 \: hydrogen \: atoms \: m ^ {- 3} $$
C'è un'intera gamma di densità critiche nel nostro spazio esterno. Ad esempio, per il mezzo intergalattico $ \ rho_c $ è 1 atomo di idrogeno $ m ^ {- 3} $, mentre per le nuvole molecolari è $ 10 ^ 6 $ atomi di idrogeno $ m ^ {- 3} $.
Dobbiamo misurare $ \ rho_c $ considerando opportuni campioni di spazio. All'interno della nostra galassia, il valore di $ \ rho_c $ è molto alto, ma la nostra galassia non è rappresentativa dell'intero universo. Quindi, dovremmo andare nello spazio dove vale il principio cosmologico, cioè distanze ≈ 300 Mpc. Guardare 300 Mpc significa guardare indietro di 1 miliardo di anni, ma è ancora l'universo attuale.
Vengono condotti sondaggi come SDSS per determinare la densità della materia effettiva. Prendono un volume 5 × 500 × 5 Mpc 3 , contano il numero di galassie e aggiungono tutta la luce proveniente da queste galassie. Assumendo che 1 L ≡ 1 M, cioè 1 luminosità solare ≡ 1 massa solare.
Facciamo una conversione da luce a massa e poi proviamo a stimare il numero di barioni in base alle particelle di materia visibile presenti in quel volume.
Per esempio,
$$ 1000L_ \ odot ≡ 1000M_ \ odot / m_p $$
Dove, m p = massa del protone.
Quindi otteniamo approssimativamente la densità dei numeri barionici $ \ Omega b ∼ = 0,025 $. Ciò implica $ \ rho b = 0,25% $ di $ \ rho_c $. Diversi sondaggi hanno prodotto un valore leggermente diverso. Quindi, nell'universo locale, la densità numerica della materia visibile è molto inferiore alla densità critica, il che significa che stiamo vivendo in un universo aperto.
La massa con un fattore 10 non è inclusa in queste indagini perché queste indagini tengono conto della radiazione elettromagnetica ma non della materia oscura. Dare, $ \ Omega_m = 0,3 - 0,4 $. Still conclude che stiamo vivendo in un universo aperto.
La materia oscura interagisce con la gravità. Molta materia oscura può fermare l'espansione. Non abbiamo ancora formalizzato come $ \ rho $ cambia nel tempo, per cui abbiamo bisogno di un altro insieme di equazioni.
La termodinamica afferma che -
$$ dQ = dU + dW $$
Per un sistema in crescita in termini di dimensioni, $ dW = P dV $. L'espansione dell'universo è modellata come adiabatica, cioè $ dQ = 0 $. Quindi, il cambiamento di volume dovrebbe avvenire dal cambiamento nell'energia interna dU.
Prendiamo un certo volume di universo di raggio di spostamento dell'unità cioè $ r_c = 1 $. Se $ \ rho $ è la densità del materiale all'interno di questo volume di spazio, allora,
$$ M = \ frac {4} {3} \ pi a ^ 3r_c ^ 3 \ rho $$
$$ U = \ frac {4} {3} \ pi a ^ 3 \ rho c ^ 2 $$
Dove, Uè la densità di energia. Cerchiamo di scoprire il cambiamento nell'energia interna con il tempo mentre l'universo si espande.
$$ \ frac {\ mathrm {d} U} {\ mathrm {d} t} = 4 \ pi a ^ 2 \ rho c ^ 2 \ frac {\ mathrm {d} a} {\ mathrm {d} t} + \ frac {4} {3} \ pi a ^ 3 c ^ 2 \ frac {\ mathrm {d} \ rho} {\ mathrm {d} t} $$
Allo stesso modo, la variazione di volume nel tempo è data da,
$$ \ frac {\ mathrm {d} V} {\ mathrm {d} t} = 4 \ pi a ^ 2 \ frac {\ mathrm {d} a} {\ mathrm {d} t} $$
Sostituendo $ dU = −P dV $. Noi abbiamo,
$$ 4 \ pi a ^ 2 (c ^ 2 \ rho + P) \ dot {a} + \ frac {4} {3} \ pi a ^ 3c ^ 2 \ dot {\ rho} = 0 $$
$$ \ dot {\ rho} +3 \ frac {\ dot {a}} {a} \ left (\ rho + \ frac {P} {c ^ 2} \ right) = 0 $$
Questo è chiamato Fluid Equation. Ci dice come la densità dell'universo cambia con il tempo.
La pressione diminuisce man mano che l'universo si espande. Ad ogni istante la pressione cambia, ma non c'è differenza di pressione tra due punti del volume considerato, quindi il gradiente di pressione è zero. Solo i materiali relativistici impartiscono pressione, la materia è priva di pressione.
L'equazione di Friedmann insieme all'equazione dei fluidi modella l'universo.
Punti da ricordare
La materia oscura interagisce con la gravità. Molta materia oscura può fermare l'espansione.
L'equazione dei fluidi ci dice come la densità dell'universo cambia nel tempo.
L'equazione di Friedmann insieme all'equazione dei fluidi modella l'universo.
Solo i materiali relativistici impartiscono pressione, la materia è priva di pressione.
In questo capitolo, discuteremo le soluzioni alle equazioni di Friedmann relative all'universo dominato dalla materia. In cosmologia, poiché vediamo tutto su larga scala, i sistemi solari, le galassie, tutto sembra essere come particelle di polvere (è così che lo vediamo con i nostri occhi), possiamo chiamarlo universo polveroso o universo di sola materia.
Nel Fluid Equation,
$$ \ dot {\ rho} = -3 \ left (\ frac {\ dot {a}} {a} \ right) \ rho -3 \ left (\ frac {\ dot {a}} {a} \ right ) \ left (\ frac {P} {c ^ 2} \ right) $$
Possiamo vedere che c'è un termine di pressione. Per un universo polveroso,P = 0, perché la densità di energia della materia sarà maggiore della pressione di radiazione e la materia non si muove con velocità relativistica.
Quindi, l'equazione del fluido diventerà,
$$ \ dot {\ rho} = -3 \ left (\ frac {\ dot {a}} {a} \ right) \ rho $$
$$ \ Rightarrow \ dot {\ rho} a + 3 \ dot {a} \ rho = 0 $$
$$ \ Rightarrow \ frac {1} {a ^ 3} \ frac {\ mathrm {d}} {\ mathrm {d} t} (a ^ 3 \ rho) = 0 $$
$$ \ Rightarrow \ rho a ^ 3 = \: costante $$
$$ \ Rightarrow \ rho \ propto \ frac {1} {a ^ 3} $$
Non c'è controintuizione in questa equazione perché la densità dovrebbe scalare come $ a ^ {- 3} $ perché il volume aumenta come $ a ^ 3 $.
Dall'ultima relazione, possiamo dire che,
$$ \ frac {\ rho (t)} {\ rho_0} = \ left [\ frac {a_0} {a (t)} \ right] ^ 3 $$
Per l'universo attuale, a, che è uguale a a0 dovrebbe essere 1. Quindi,
$$ \ rho (t) = \ frac {\ rho_0} {a ^ 3} $$
In un universo piatto dominato dalla materia, k = 0. Quindi, l'equazione di Friedmann diventerà,
$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G \ rho} {3} $$
$$ \ dot {a} ^ 2 = \ frac {8 \ pi G \ rho a ^ 2} {3} $$
Risolvendo questa equazione, otterremo,
$$ a \ propto t ^ {2/3} $$
$$ \ frac {a (t)} {a_0} = \ left (\ frac {t} {t_0} \ right) ^ {2/3} $$
$$ a (t) = \ left (\ frac {t} {t_0} \ right) ^ {2/3} $$
Ciò significa che l'universo continuerà ad aumentare con una velocità decrescente. L'immagine seguente mostra l'espansione di un universo polveroso.

Come cambia ρ nel tempo?
Dai un'occhiata alla seguente equazione:
$$ \ frac {\ rho (t)} {\ rho_0} = \ left (\ frac {t_0} {t} \ right) ^ 2 $$
Sappiamo che il fattore di scala cambia nel tempo come $ t ^ {2/3} $. Così,
$$ a (t) = \ left (\ frac {t} {t_0} \ right) ^ {2/3} $$
Differenziandolo, otterremo,
$$ \ frac {(da)} {dt} = \ dot {a} = \ frac {2} {3} \ left (\ frac {t ^ {- 1/3}} {t_0} \ right) $$
Sappiamo che il file Hubble Constant è,
$$ H (t) = \ frac {\ dot {a}} {a} = \ frac {2} {3t} $$
Questa è l'equazione per Einstein-de sitter Universe. Se vogliamo calcolare l'età attuale dell'universo, allora,
$$ t_0 = t_ {age} = \ frac {2} {3H_0} $$
Dopo aver inserito il valore di $ H_0 $ per l'universo attuale, otterremo il valore dell'età dell'universo come 9 Gyrs. Ci sono moltiGlobular Cluster nella nostra galassia della Via Lattea che ha un'età superiore a quella.
Riguardava l'universo polveroso. Ora, se presumi che l'universo sia dominato dalla radiazione e non dalla materia, la densità di energia della radiazione diventa $ a ^ {- 4} $ anziché $ a ^ {- 3} $. Ne vedremo di più nel prossimo capitolo.
Punti da ricordare
In cosmologia, tutto sembra essere come particelle di polvere, quindi lo chiamiamo universo polveroso o universo di sola materia.
Se assumiamo che l'universo sia dominato dalla radiazione e non dalla materia, allora la densità di energia della radiazione è $ a ^ {- 4} $ anziché $ a ^ {- 3} $.
In questo capitolo, discuteremo le soluzioni alle equazioni di Friedmann relative all'universo dominato dalle radiazioni. All'inizio confrontiamo la densità energetica della materia con quella della radiazione. Questo ci consentirà di vedere se il nostro universo è dominato dalla materia o dalle radiazioni.
Densità energetica delle radiazioni
La radiazione prevalente nell'universo attuale può essere attribuita molto poco alle sorgenti stellari, ma è principalmente dovuta al residuo CMB (Cosmic Microwave Background).
La densità di energia della radiazione, $ \ epsilon _ {\ gamma, 0} $, può essere espressa come segue:
$$ \ epsilon _ {\ gamma, 0} = aT_0 ^ 4 $$
Qui, a è la costante di radiazione che ha l'espressione $ (8 \ pi ^ 5k_B ^ 4) / (15h ^ 3c ^ 2) $ uguale a a = 7.5657 × 10−15erg\: cm−3 K−4. La Temperatura, T0, che qui consideriamo, corrisponde a quella del corpo nero corrispondente alla CMB.
Sostituendo i risultati, abbiamo,
$$ \ epsilon _ {\ gamma, 0} = aT_0 ^ 4 = 4 \ volte 10 ^ {- 13} erg \: cm ^ {- 3} $$
Densità energetica della materia
Nei calcoli seguenti, abbiamo l'ipotesi di lavorare con un universo piatto e K = 0. Consideriamo la densità energetica della materia come $ \ epsilon = \ rho c ^ 2 $. Consideriamo quanto segue:
$$ \ rho_ {m, 0} c ^ 2 = 0,3 \ rho_ {c, 0} c ^ 2 = 0,3 \ times \ frac {3H_0 ^ 2} {8 \ pi G} \ times c ^ 2 $$
$$ \ rho_ {m, 0} c ^ 2 \ simeq 2 \ times 10 ^ {- 8} erg \: cm ^ {- 3} $$
$$ \ rho_ {b, 0} c ^ 2 = 0,03 \ rho_ {c, 0} c ^ 2 = 0,03 \ times \ frac {3H_0 ^ 2} {8 \ pi G} \ times c ^ 2 $$
$$ \ rho_ {b, 0} c ^ 2 \ simeq 2 \ times 10 ^ {- 9} erg \: cm ^ {- 3} $$
Quindi, dal calcolo di cui sopra, vediamo che viviamo in un universo dominato dalla materia. Ciò può essere supportato dal fatto che la CMB è molto fredda. Guardando indietro nel tempo, avremmo la temperatura della CMB sempre più calda e saremo in grado di concludere che potrebbe esserci stata un'epoca in cui l'universo era dominato dalle radiazioni.
Variazione di densità e fattore di scala
L'equazione del fluido ci mostra che:
$$ \ dot {\ rho} + 3 \ frac {\ dot {a}} {a} \ left (\ rho + \ frac {P} {c ^ 2} \ right) = 0 $$
Se consideriamo un universo polveroso, avremmo P = 0. Mettendo da parte i risultati precedenti, consideriamo l'universo dominato dalla radiazione.
$$ \ dot {\ rho} _ {rad} + 3 \ frac {\ dot {a}} {a} \ left (\ rho_ {rad} + \ frac {P} {c ^ 2} \ right) = 0 $$
Usando la relazione di pressione di $ P_ {rad} = \ rho c ^ {2/3} $ abbiamo -
$$ \ dot {\ rho} _ {rad} + 3 \ frac {\ dot {a}} {a} \ left (\ rho_ {rad} + \ frac {\ rho_ {rad}} {3} \ right) = 0 $$
$$ \ dot {\ rho} _ {rad} + 4 \ frac {\ dot {a}} {a} (\ rho_ {rad}) = 0 $$
Con un'ulteriore semplificazione, abbiamo,
$$ \ frac {1} {a ^ 4} \ frac {\ mathrm {d}} {\ mathrm {d} t} (\ rho_ {rad} a ^ 4) = 0 $$
$$ \ rho_ {rad} a ^ 4 = \: costante $$
$$ \ rho_ {rad} \ propto \ frac {1} {a ^ 4} $$
Il risultato mostra sopra un inverso 4 ° variazione di potenza di una con $ \ rho $.
Questo può essere interpretato fisicamente come $ a ^ {- 3} $ proveniente dalla variazione di volume man mano che aumenta. Il restante $ a ^ {- 1} $ può essere trattato come l'energia persa dal fotone a causa dell'espansione dello spazio nell'universo (spostamento verso il rosso cosmologico 1 + z = a -1 ).
L'immagine seguente mostra la variazione della materia e della densità di radiazione nel tempo.
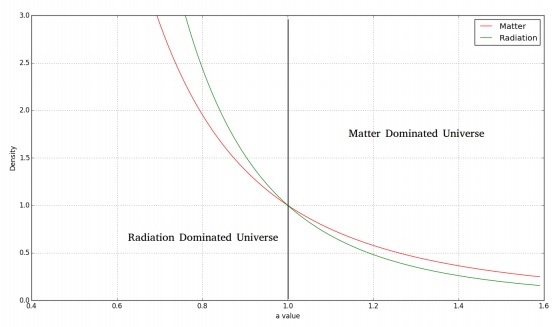
Per un universo piatto, dominato dalla radiazione, avremmo l'equazione di Friedmann come segue:
$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G \ rho} {3} $$
$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ frac {\ rho_0} {a ^ 4} $$
Sulla semplificazione e applicando la soluzione all'equazione differenziale, abbiamo:
$$ (\ dot {a}) ^ 2 = \ frac {8 \ pi G \ rho_0} {3a ^ 2} $$
$$ \ Rightarrow a (t) \ propto t ^ {\ frac {1} {2}} $$
Quindi, abbiamo -
$$ a (t) = a_0 \ left (\ frac {t} {t_0} \ right) ^ {\ frac {1} {2}} $$
Dall'equazione di cui sopra, vediamo che il tasso di aumento del fattore di scala è inferiore a quello dell'universo polveroso.
Punti da ricordare
Le radiazioni prevalenti nell'universo attuale possono essere attribuite molto poco alle sorgenti stellari.
Per un universo polveroso, la pressione è zero.
CMB è molto freddo.
L'area dell'Energia Oscura è un'area molto grigia in astronomia perché è un parametro libero in tutte le equazioni, ma non c'è un'idea chiara di cosa sia esattamente.
Inizieremo con le equazioni di Friedmann,
$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho - \ frac {k \ ast c ^ 2} {a ^ 2} $$
La maggior parte dei libri elementari sulla cosmologia, iniziano tutti con la descrizione dell'energia oscura di questo episodio che prima dell'osservazione di Hubble, l'universo è chiuso e statico.
Ora, affinché l'universo sia statico nella parte destra, entrambi i termini dovrebbero corrispondere e dovrebbero essere zero, ma se il primo termine è maggiore del secondo termine, l'universo non sarà statico, quindi Einstein ha abbandonato il parametro libero ∧ nell'equazione di campo per rendere statico l'universo, quindi ha sostenuto che non importa quale sia il primo termine confrontato con il secondo termine, è sempre possibile ottenere un universo statico se c'è un altro componente nell'equazione, che può compensare il dis- corrispondenza tra questi due termini.
$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho - \ frac {k \ ast c ^ 2} {a ^ 2} + \ frac {\ wedge} {3} $$
$$ \ left (\ frac {\ ddot {a}} {a} \ right) = - \ frac {4 \ pi G} {3} \ left (\ rho + \ frac {3P} {c ^ 2} \ destra) + \ frac {\ wedge} {3} $$
Dove $ P = \ rho \ ast c ^ 2/3 $ e $ \ wedge = \ rho \ ast c ^ 2 $ è il parametro cosmologico. (Il segno negativo è solo a causa dell'attrazione)
Nell'equazione sopra (equazione dell'accelerazione) -
$ 3P / c ^ 2 $ è la pressione negativa dovuta alla radiazione,
$ -4 \ pi G / 3 $ è l'attrazione dovuta alla gravità, e
$ \ wedge / 3 $ fornisce un contributo positivo.
Il terzo termine agisce come una forza repulsiva perché un'altra parte dell'equazione è attraente.
Il significato fisico dell'equazione è questo ˙a = 0perché non c'era alcuna prova che dimostri che l'universo si sta espandendo. Cosa succede se questi due termini non corrispondono tra loro, quindi è meglio aggiungere un componente e, a seconda dell'offset, possiamo sempre modificare il valore del parametro libero.
Quella volta non c'era una spiegazione fisica su questi parametri cosmologici, motivo per cui quando la spiegazione dell'universo in espansione fu scoperta negli anni '20, dove Einstein subito ha dovuto eliminare questa costante.
La spiegazione di questo cosmological constant è ancora in uso perché spiega una versione diversa dell'universo, ma la definizione di questa costante cosmologica, il modo di interpretare ha continuato a cambiare nel tempo.
Ora il concetto di questa costante cosmologica è stato riportato alla cosmologia per molte ragioni. Uno dei motivi è che abbiamo osservazioni per la densità di energia di diversi componenti dell'universo (barione, materia oscura, radiazione), quindi sappiamo qual è questo parametro. Osservazioni indipendenti utilizzandocosmic microwave background mostra che k = 0.
$$ CMB, k = 0 \: \ rho = \ rho_c = \ frac {3H_0 ^ 2} {8 \ pi G} \ approx 10 \: Hydrogen \: atoms.m ^ {- 3} $$
Affinché k sia 0, $ \ rho $ dovrebbe essere uguale a $ \ rho_c $, ma tutto ciò che sappiamo se lo sommiamo non dà 0, il che significa che c'è qualche altro componente che mostra che è molto inferiore a $ \ rho_c $.
$$ \ rho = \ rho_b + \ rho_ {DM} + \ rho_ {rad} << \ rho_c $$
Un'altra prova di energia oscura viene dal Type 1 Supernova Observationche si verifica quando la nana bianca accresce la materia e supera il limite di Chandrashekhar, che è un limite molto preciso (≈ 1.4M). Ora, ogni volta che si verifica l'esplosione di una supernova di tipo 1, abbiamo la stessa massa, il che significa che l'energia di legame totale del sistema è la stessa e la quantità di energia luminosa che possiamo vedere è la stessa.
Ovviamente, la luce della supernova aumenta e poi svanisce, ma se misuri la luminosità massima sarà sempre la stessa, il che la rende un candidato standard. Quindi, con una supernova di tipo 1 abbiamo misurato la componente cosmologica dell'universo e gli astronomi hanno scoperto che la supernova con spostamento verso il rosso alto è del 30% - 40% più debole della supernova con spostamento verso il rosso basso e può essere spiegato se c'è qualche non -zero∧ termine.
Nei modelli cosmologici DE (Dark Energy)è trattato come un fluido, il che significa che possiamo scrivere l'equazione di stato per esso. L'equazione di stato è l'equazione che collega le variabili come pressione, densità, temperatura e volume di due diversi stati della materia.
Dimensionalmente vediamo,
$$ \ frac {8 \ pi G} {3} \ rho = \ frac {\ wedge} {3} $$
$$ \ rho_ \ wedge = \ frac {\ wedge} {8 \ pi G} $$
Densità energetica di DE,
$$ \ epsilon_ \ wedge = \ rho_ \ wedge \ ast c ^ 2 = \ frac {\ wedge c ^ 2} {8 \ pi G} $$
Parametro di densità di energia oscura,
$$ \ Omega_ \ wedge = \ frac {\ rho_ \ wedge} {\ rho_c} $$
$ \ Omega_ \ wedge $ è la densità dell'energia oscura in termini di densità critica.
$$ \ rho = \ rho_b + \ rho_ {DM} + \ rho_ \ wedge $$
Esistono numerose teorie sull'energia oscura, che sta respingendo l'universo e causando l'espansione dell'universo. Un'ipotesi è che questa energia oscura potrebbe essere una densità di energia del vuoto. Supponiamo che lo spazio stesso stia elaborando una certa energia e quando conti la quantità di materia barionica, materia oscura e radiazione all'interno del volume unitario dello spazio, stai anche contando la quantità di energia associata allo spazio, ma non è chiaro che l'energia oscura è davvero una densità di energia del vuoto.
Sappiamo che la relazione tra densità e fattore di scala per la materia oscura e la radiazione sono,
$$ \ rho_m \ propto \ frac {1} {a ^ 3} $$
$$ \ rho_m \ propto \ frac {1} {a ^ 4} $$
Abbiamo il grafico del fattore di scala della densità v / s. Nello stesso grafico, possiamo vedere che $ \ rho_ \ wedge $ è una costante con l'espansione dell'universo che non dipende dal fattore di scala.
L'immagine seguente mostra la relazione tra densità e fattore di scala.

‘ρ’ v/s ‘a’(fattore di scala che è correlato al tempo) nello stesso grafico, l'energia oscura è modellata come una costante. Quindi, qualunque energia oscura misuriamo nell'universo attuale, è una costante.
Punti da ricordare
Osservazioni indipendenti che utilizzano lo sfondo cosmico a microonde mostrano che k = 0.
$ \ rho_ \ wedge $ è una costante con l'espansione dell'universo che non dipende dal fattore di scala.
Anche la gravità sta cambiando con il tempo che viene chiamato modified Newtonian dynamics.
In questo capitolo, discuteremo delle curve di rotazione della galassia a spirale e delle prove per la materia oscura.
Materia oscura e fatti osservativi sulla materia oscura
La prima prova della materia oscura era il study of the Kinematics of Spiral Galaxy.
Il Sole è spostato di 30.000 anni luce dal centro della nostra galassia. La velocità centrica galattica è di 220 km / s.
Perché la velocità di 220 km / s non è 100 km / so 500 km / s? Cosa governa il movimento circolare dell'oggetto?
La massa racchiusa nel raggio aiuta a rilevare la velocità nell'universo.
Rotazione della Via Lattea o galassia a spirale - Rotazione differenziale
Angular Velocity varia con la distanza dal centro.
Il periodo di tempo orbitale dipende dalla distanza dal centro.
Il materiale più vicino al centro galattico ha un periodo di tempo più breve e il materiale lontano dal centro galattico ha un periodo di tempo più ampio.
Curva di rotazione
Prevedi il cambiamento di velocità con il Galactic centric radius. La curva che dà la velocità cambia con il raggio orbitale.
Quando vediamo le cose muoversi, pensiamo che sia la gravità che influenza la rotazione.
La distribuzione della massa varia con il raggio. La densità della materia predice la curva di rotazione. La curva di rotazione basata sulla densità della materia, che varia con il raggio.
Luminosità superficiale
Scegliamo il cerotto e vediamo quanta luce esce.
La quantità di luce proveniente dal cerotto viene chiamata luminosità della superficie.
La sua unità è mag/arcsec2.
Se troviamo che la luminosità della superficie varia con il raggio, possiamo scoprire che la materia luminosa varia con il raggio.
$$ \ mu (r) \ propto exp \ left (\ frac {-r} {h_R} \ right) $$
$ h_R $ è la lunghezza della scala. $ \ mu (r) = \ mu_o \ ast exp \ left (\ frac {-r} {h_R} \ right) $
$ h_R $ è quasi 3 kpc per la Via Lattea.
Galassie a spirale
Affinché gli astronomi comprendano la curva di rotazione, hanno diviso le galassie in due componenti, che sono:
- Disk
- Bulge
L'immagine seguente mostra un rigonfiamento sferico centrale + disco circolare. La distribuzione stellare e del gas è diversa nel rigonfiamento e nel disco.

Cinematica delle galassie a spirale
-
La velocità circolare di qualsiasi oggetto - Per il rigonfiamento è (r <Rb).
$$ V ^ 2 (r) = G \ ast \ frac {M (r)} {r} $$
$$ M (r) = \ frac {4 \ pi r ^ 3} {3} \ ast \ rho_b $$
-
Per il disco - (Rb <r <Rd)
$$ V ^ 2 (r) = G \ ast \ frac {M (r)} {r} $$
Bulge ha una densità di stelle più o meno costante.
La densità all'interno del rigonfiamento è costante (non cambia con la distanza all'interno del rigonfiamento).
In un disco, la densità stellare diminuisce con il raggio. Il raggio aumenta poi la materia luminosa diminuisce.
In blocco - $ V (r) \ propto r $
Nel disco - $ V (r) \ propto 1 / \ sqrt {r} $
Curva di rotazione delle galassie a spirale
Tramite la Spectroscopy (galassie vicine - risolte spazialmente la galassia), produciamo la curva di rotazione.
Come accennato in precedenza, vediamo che la curva di rotazione è piatta nelle regioni esterne, cioè le cose si muovono velocemente nelle regioni esterne, che generalmente non dovrebbe essere in questa forma.
La velocità orbitale aumenta con l'aumento del raggio della regione interna, ma si appiattisce nella regione esterna.
Materia oscura
Si dice che la Materia Oscura sia la Componente Non Luminosa dell'Universo. Cerchiamo di capire la materia oscura attraverso i seguenti suggerimenti.
Le curve di rotazione piatte sono contrarie a ciò che vediamo per la distribuzione di stelle e gas nelle galassie a spirale.
La luminosità della superficie del disco diminuisce in modo esponenziale con il raggio, il che implica che la massa della materia luminosa, principalmente stelle, è concentrata attorno al centro galattico.
L'appiattimento della curva di rotazione suggerisce che la massa totale della galassia entro un certo raggio r è in aumento sempre con l'aumento di r.
Questo può essere spiegato solo se c'è una grande quantità di massa gravitante invisibile in queste galassie che non emette radiazioni elettromagnetiche.
Le misurazioni della curva di rotazione delle galassie a spirale sono una delle prove più convincenti per la materia oscura.
Prove di materia oscura
Missing Mass - 10 volte la massa luminosa.
La maggior parte di questa materia oscura deve trovarsi nell'alone della galassia: grandi quantità di materia oscura nel disco possono disturbare la stabilità a lungo termine del disco contro le forze di marea.
Una piccola frazione della materia oscura nel disco può essere barionica - stelle deboli (nane brune, nane nere) e resti stellari compatti (stelle di neutroni, buchi neri). Ma tale materia oscura barionica non può spiegare la scala completa della massa mancante nelle galassie.
Profilo di densità della materia oscura - $ M (r) \ propto r $ e $ \ rho (r) \ propto r ^ {- 2} $.
I dati della curva di rotazione per le galassie a spirale sono coerenti con la materia oscura distribuita nel loro alone.
Questo alone scuro costituisce gran parte della massa totale della galassia.
Tutta la materia barionica (stelle, ammassi stellari, ISM, ecc.) È tenuta insieme dal potenziale gravitazionale di questo alone di materia oscura.
Conclusione
La materia oscura è stata rilevata solo attraverso la loro interazione gravitazionale con una materia ordinaria. Non è stata ancora osservata alcuna interazione con la luce (nessuna forza elettromagnetica).
Neutrinos- Carica meno, interagisce debolmente, ma la massa è troppo inferiore (<0,23 eV). Le particelle di DM dovrebbero avere E> 10 eV circa per spiegare la formazione della struttura.
Le particelle massicce a interazione debole (WIMPS) possono essere la fonte della materia oscura.
Punti da ricordare
Il materiale più vicino al centro galattico ha un periodo di tempo più breve.
Bulge ha una densità di stelle più o meno costante.
La luminosità della superficie del disco diminuisce esponenzialmente con il raggio.
Grandi quantità di materia oscura nel disco possono disturbare la stabilità a lungo termine del disco contro le forze di marea.
La prima prova diretta della materia oscura venne da Frids Ricky. Fece alcune osservazioni che rivelarono per la prima volta la materia oscura. Le sue osservazioni hanno considerato il movimento complessivo all'interno dell'ammasso galattico.
Gli oggetti estesi sono ammassi di galassie e sono considerati strutture legate. Queste galassie si muovono rispetto al centro dell'ammasso ma non volano via. Guardiamo il movimento complessivo della galassia.
Presupposto: le velocità sono rappresentative del potenziale sottostante
Ogni galassia avrà il proprio moto proprio all'interno dell'ammasso e Hubble Flow Component. Le galassie più piccole sono più piccole, la maggior parte della luce proviene da M31 e MW, ci sono diverse galassie nane. Per la nostra analisi grezza, possiamo usare solo M31 e MW e valutare la massa dinamica del gruppo locale.
C'è una velocità relativa tra noi e M31. È rozzo, ma è vero. La storia inizia molto tempo fa, quando M31 e MW erano vicini l'uno all'altro, perché erano membri di un ammasso che si stavano allontanando l'uno dall'altro. Dopo qualche tempo raggiungono la massima separazione, quindi si avvicinano l'uno all'altro.
Diciamo che la separazione massima che può mai raggiungere è $ r_ {max} $. Ora hanno una separazione chiamatar. PermettereMessere la massa combinata di MW e M31. Non sappiamo quando viene raggiunto $ r_ {max} $.
$$ \ frac {GM} {r_ {max}} = \: Potenziale \: a \: r_ {max} $$
Quando queste galassie si stavano avvicinando l'una all'altra in un istante r, allora l'energia del sistema sarà -
$$ \ frac {1} {2} \ sigma ^ 2 = \ frac {GM} {r} = \ frac {GM} {r_ {max}} $$
σ è la velocità relativa di entrambe le galassie. M è solo massa ridotta, ma la massa di prova è 1. σ è la velocità di qualsiasi oggetto a distanza rdal centro del cluster. Crediamo che questo cluster sia in equazione dinamica perché vale il teorema viriale. Quindi, le galassie non possono venire con velocità diverse.
Quanto tempo impiegherebbero queste galassie per raggiungere la massima distanza?
Per capire questo, consideriamo la seguente equazione.
$$ \ frac {1} {2} \ left (\ frac {dr} {dt} \ right) ^ 2 = \ frac {GM} {r} - \ frac {GM} {r_ {max}} $$
$$ t_ {max} = \ int_ {0} ^ {r_ {max}} dt = \ int_ {0} ^ {r_ {max}} \ frac {dr} {\ sqrt {2GM}} \ left (\ frac {1} {r} - \ frac {1} {r_ {max}} \ right) ^ 2 $$
$$ t_ {max} = \ frac {\ pi r_ {max} ^ {\ frac {3} {2}}} {2 \ sqrt {2GM}} $$
Dove, M = massa dinamica del gruppo locale. Il tempo totale dall'inizio alla fine della collisione è $ 2t_ {max} $. Perciò,
$$ 2t_ {max} = t_0 + \ frac {D} {\ sigma} $$
E $ t_0 $ è l'era presente dell'universo.
Se effettivo $ t_ {max} <RHS $, allora abbiamo un limite inferiore per il tempo. $ D / \ sigma $ è il momento in cui si scontreranno di nuovo. Qui, abbiamo assunto σ come costante.
$$ t_ {max} = \ frac {t_0} {2} + \ frac {D} {2 \ sigma} $$
$$ r_ {max} = t_ {max} \ times \ sigma = 770K_ {pc} $$
Qui, σ = velocità relativa tra MW e M31.
$$ M_ {dinamico} = 3 \ volte 10 ^ {12} M_0 $$
$$ M_ {MW} ^ {lum} = 3 \ volte 10 ^ {10} M_0 $$
$$ M_ {M31} ^ {lum} = 3 \ volte 10 ^ {10} M_0 $$
Ma praticamente, la massa dinamica viene rilevata considerando ogni galassia all'interno dell'ammasso. La massa mancante è la materia oscura eFrids Rickyho notato che le galassie nell'ammasso di coma si stanno muovendo troppo velocemente. Ha predetto l'esistenza di stelle di neutroni l'anno successivo alla scoperta delle stelle di neutroni e ha utilizzato il telescopio Palomar per trovare la supernova.
Punti da ricordare
La prima prova diretta della materia oscura venne da Frids Ricky.
Gli oggetti estesi sono ammassi di galassie e vengono considerati bound structures.
Dynamic mass viene scoperto considerando ogni galassia all'interno dell'ammasso.
In questo capitolo, discuteremo dei parametri Density e Hubble.
Parametro di Hubble
Il parametro Hubble è definito come segue:
$$ H (t) \ equiv \ frac {da / dt} {a} $$
che misura la rapidità con cui cambia il fattore di scala. Più in generale, l'evoluzione del fattore di scala è determinata dall'equazione di Friedmann.
$$ H ^ 2 (t) \ equiv \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho - \ frac {kc ^ 2} {a ^ 2} + \ frac {\ wedge} {3} $$
dove, ∧ è una costante cosmologica.
Per un universo piatto, k = 0, quindi l'equazione di Friedmann diventa -
$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho + \ frac {\ wedge} {3} $$
Per un universo dominato dalla materia, la densità varia come -
$$ \ frac {\ rho_m} {\ rho_ {m, 0}} = \ left (\ frac {a_0} {a} \ right) ^ 3 \ Rightarrow \ rho_m = \ rho_ {m, 0} a ^ {- 3} $$
e, per un universo dominato dalle radiazioni, la densità varia come -
$$ \ frac {\ rho_ {rad}} {\ rho_ {rad, 0}} = \ left (\ frac {a_0} {a} \ right) ^ 4 \ Rightarrow \ rho_ {rad} = \ rho_ {rad, 0} a ^ {- 4} $$
Attualmente viviamo in un universo dominato dalla materia. Quindi, considerando $ \ rho ≡ \ rho_m $, otteniamo -
$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho_ {m, 0} a ^ {- 3} + \ frac {\ wedge} {3} $$
La costante cosmologica e la densità di energia oscura sono correlate come segue:
$$ \ rho_ \ wedge = \ frac {\ wedge} {8 \ pi G} \ Rightarrow \ wedge = 8 \ pi G \ rho_ \ wedge $$
Da questo, otteniamo -
$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho_ {m, 0} a ^ {- 3} + \ frac {8 \ pi G} {3} \ rho_ \ wedge $$
Inoltre, la densità critica e la costante di Hubble sono correlate come segue:
$$ \ rho_ {c, 0} = \ frac {3H_0 ^ 2} {8 \ pi G} \ Rightarrow \ frac {8 \ pi G} {3} = \ frac {H_0 ^ 2} {\ rho_ {c, 0}} $$
Da questo, otteniamo -
$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {H_0 ^ 2} {\ rho_ {c, 0}} \ rho_ {m, 0} a ^ {- 3} + \ frac {H_0 ^ 2} {\ rho_ {c, 0}} \ rho_ \ wedge $$
$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = H_0 ^ 2 \ Omega_ {m, 0} a ^ {- 3} + H_0 ^ 2 \ Omega _ {\ wedge, 0 } $$
$$ (\ dot {a}) ^ 2 = H_0 ^ 2 \ Omega_ {m, 0} a ^ {- 1} + H_0 ^ 2 \ Omega _ {\ wedge, 0} a ^ 2 $$
$$ \ left (\ frac {\ dot {a}} {H_0} \ right) ^ 2 = \ Omega_ {m, 0} \ frac {1} {a} + \ Omega _ {\ wedge, 0} a ^ 2 $$
$$ \ left (\ frac {\ dot {a}} {H_0} \ right) ^ 2 = \ Omega_ {m, 0} (1 + z) + \ Omega _ {\ wedge, 0} \ frac {1} { (1 + z) ^ 2} $$
$$ \ left (\ frac {\ dot {a}} {H_0} \ right) ^ 2 (1 + z) ^ 2 = \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega _ {\ wedge , 0} $$
$$ \ left (\ frac {\ dot {a}} {H_0} \ right) ^ 2 \ frac {1} {a ^ 2} = \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega_ {\ wedge, 0} $$
$$ \ left (\ frac {H (z)} {H_0} \ right) ^ 2 = \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega _ {\ wedge, 0} $$
Qui $ H (z) $ è il parametro di Hubble dipendente dallo spostamento verso il rosso. Questo può essere modificato per includere il parametro di densità di radiazione $ \ Omega_ {rad} $ e il parametro di densità di curvatura $ \ Omega_k $. L'equazione modificata è -
$$ \ left (\ frac {H (z)} {H_0} \ right) ^ 2 = \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega_ {rad, 0} (1 + z) ^ 4+ \ Omega_ {k, 0} (1 + z) ^ 2 + \ Omega _ {\ wedge, 0} $$
$$ Oppure, \: \ left (\ frac {H (z)} {H_0} \ right) ^ 2 = E (z) $$
$$ Oppure \: H (z) = H_0E (z) ^ {\ frac {1} {2}} $$
dove,
$$ E (z) \ equiv \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega_ {rad, 0} (1 + z) ^ 4 + \ Omega_ {k, 0} (1 + z) ^ 2 + \ Omega _ {\ wedge, 0} $$
Questo mostra che il parametro Hubble varia nel tempo.
Per il Einstein-de Sitter Universo, $ \ Omega_m = 1, \ Omega_ \ wedge = 0, k = 0 $.
Inserendo questi valori, otteniamo:
$$ H (z) = H_0 (1 + z) ^ {\ frac {3} {2}} $$
che mostra l'evoluzione temporale del parametro Hubble per l'universo di Einstein-de Sitter.
Parametro di densità
Il parametro di densità, $ \ Omega $, è definito come il rapporto tra la densità effettiva (o osservata) ρ e la densità critica $ \ rho_c $. Per qualsiasi quantità $ x $ il parametro di densità corrispondente, $ \ Omega_x $ può essere espresso matematicamente come -
$$ \ Omega_x = \ frac {\ rho_x} {\ rho_c} $$
Per le diverse quantità in esame, possiamo definire i seguenti parametri di densità.
| S.No. | Quantità | Parametro di densità |
|---|---|---|
| 1 | Barioni | $ \ Omega_b = \ frac {\ rho_b} {\ rho_c} $ |
| 2 | Materia (barionica + oscura) | $ \ Omega_m = \ frac {\ rho_m} {\ rho_c} $ |
| 3 | Energia oscura | $ \ Omega_ \ wedge = \ frac {\ rho_ \ wedge} {\ rho_c} $ |
| 4 | Radiazione | $ \ Omega_ {rad} = \ frac {\ rho_ {rad}} {\ rho_c} $ |
Dove i simboli hanno il loro significato abituale.
Punti da ricordare
L'evoluzione del fattore di scala è determinata dal Friedmann Equation.
H(z) è il parametro Hubble dipendente dallo spostamento verso il rosso.
Il Hubble Parameter varia nel tempo.
Il Density Parameter è definito come il rapporto tra la densità effettiva (o osservata) e la densità critica.
Come discusso nei capitoli precedenti, l'evoluzione temporale del parametro Hubble è data da:
$$ H (z) = H_0E (z) ^ {\ frac {1} {2}} $$
Dove z è il passaggio al rosso e E(Z) è -
$$ E (z) \ equiv \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega (1 + z) ^ 4 + \ Omega_ {k, 0} (1 + z) ^ 2 + \ Omega ^ {\ wedge, 0} $$
Se l'espansione dell'universo è costante, la vera età dell'universo è data come segue:
$$ t_H = \ frac {1} {H_0} $$
Se è l'universo dominato dalla materia, cioè l'universo di Einstein Desitter, allora la vera età dell'universo è data da:
$$ t_H = \ frac {2} {3H_0} $$
Scale e Redshift sono definiti da:
$$ a = \ frac {a_0} {1 + z} $$
L'età dell'universo in termini di parametro cosmologico è derivata come segue.
Il parametro Hubble è dato da -
$$ H = \ frac {\ frac {da} {dt}} {a} $$
Differenziando, otteniamo -
$$ da = \ frac {-dz} {(1 + z) ^ 2} $$
Dove a0 = 1 (valore attuale del fattore di scala)
$$ \ frac {\ mathrm {d} a} {\ mathrm {d} t} = \ frac {-1} {(1 + z) ^ 2} $$
$$ \ frac {\ mathrm {d} a} {\ mathrm {d} t} = \ frac {\ mathrm {d} a} {\ mathrm {d} t} \ frac {\ mathrm {d} z} { \ mathrm {d} t} $$
$$ H = \ frac {\ dot {a}} {a} = \ frac {\ mathrm {d} a} {\ mathrm {d} t} \ frac {\ mathrm {d} z} {\ mathrm {d } t} \ frac {1 + z} {1} $$
$$ \ frac {\ dot {a}} {a} = \ frac {-1} {1 + z} \ frac {\ mathrm {d} z} {\ mathrm {d} t} \ frac {1} { 1} $$
$$ H (z) = H_0E (z) ^ {\ frac {1} {2}} $$
$$ dt = \ frac {-dz} {H_0E (z) ^ {\ frac {1} {2}} (1 + z)} $$
Se vogliamo trovare l'età dell'universo a un dato spostamento verso il rosso ‘z’ poi -
$$ t (z) = \ frac {1} {H_0} \ int _ {\ infty} ^ {z_1} \ frac {-1} {E (z) ^ {\ frac {1} {2}} (1+ z)} dz $$
Dove k è il parametro della densità di curvatura e -
$$ E (z) \ equiv \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega_ {rad, 0} (1 + z) ^ 4 + \ Omega_ {k, 0} (1 + z) ^ 2 + \ Omega _ {\ wedge, 0} $$
Per calcolare l'età attuale dell'universo, prendi z1 = 0.
$$ t (z = 0) = t_ {age} = t_0 = \ frac {1} {H_0} \ int _ {\ infty} ^ {z_1} \ frac {-1} {E (z) ^ {\ frac { 1} {2}} (1 + z)} dz $$
Per il modello Einstein Desitter, ovvero $ \ Omega_m = 1 $, $ \ Omega_ {rad} = 0 $, $ \ Omega_k = 0 $, $ \ Omega_ \ wedge = 0 $, l'equazione per l'età dell'universo diventa -
$$ t_ {age} = \ frac {1} {H_0} \ int_ {0} ^ {\ infty} \ frac {1} {(1 + z) ^ {\ frac {5} {2}}} dz $ $
Dopo aver risolto l'integrale, otteniamo:
$$ t_H = \ frac {2} {3H_0} $$
Il cielo notturno è come un Cosmic Time Machine.Ogni volta che osserviamo un pianeta, una stella o una galassia lontani, lo vediamo com'era ore, secoli o addirittura millenni fa. Questo perché la luce viaggia a una velocità finita (la velocità della luce) e date le grandi distanze nell'Universo, non vediamo gli oggetti come sono ora, ma come erano quando la luce è stata emessa. Il tempo trascorso tra - quando rileviamo la luce qui sulla Terra e quando è stata originariamente emessa dalla sorgente, è noto comeLookback Time (tL(z1)).
Quindi, il tempo di ricerca è dato da:
$$ t_1 (z_1) = t_0-t (z_1) $$
Il tempo di ricerca per l'Universo Einstein Desitter è -
$$ t_L (z) = \ frac {2} {3H_0} \ left [1- \ frac {1} {(1 + z) ^ {\ frac {3} {2}}} \ right] $$
Punti da ricordare
Ogni volta che osserviamo un pianeta, una stella o una galassia lontani, lo vediamo com'era ore, secoli o addirittura millenni fa.
Il tempo trascorso tra il momento in cui rileviamo la luce qui sulla Terra e il momento in cui è stata originariamente emessa dalla sorgente è noto come tempo di ricerca.
In questo capitolo, capiremo cos'è la distanza del diametro angolare e come aiuta in cosmologia.
Per l'universo attuale -
$ \ Omega_ {m, 0} \: = \: 0.3 $
$ \ Omega _ {\ wedge, 0} \: = \: 0.69 $
$ \ Omega_ {rad, 0} \: = \: 0.01 $
$ \ Omega_ {k, 0} \: = \: 0 $
Finora abbiamo studiato due tipi di distanze:
Proper distance (lp) - La distanza percorsa dai fotoni dalla sorgente a noi, ovvero The Instantaneous distance.
Comoving distance (lc) - Distanza tra gli oggetti in uno spazio che non si espande, ovvero distance in a comoving frame of reference.
Distanza come funzione del Redshift
Considera una galassia che irradia un fotone alla volta t1 che viene rilevato dall'osservatore in t0. Possiamo scrivere la giusta distanza dalla galassia come -
$$ l_p = \ int_ {t_1} ^ {t_0} cdt $$
Lascia che sia il redshift della galassia z,
$$ \ Rightarrow \ frac {\ mathrm {d} z} {\ mathrm {d} t} = - \ frac {1} {a ^ 2} \ frac {\ mathrm {d} a} {\ mathrm {d} t} $$
$$ \ Rightarrow \ frac {\ mathrm {d} z} {\ mathrm {d} t} = - \ frac {\ frac {\ mathrm {d} a} {\ mathrm {d} t}} {a} \ frac {1} {a} $$
$$ \ quindi \ frac {\ mathrm {d} z} {\ mathrm {d} t} = - \ frac {H (z)} {a} $$
Ora, spostandosi a distanza della galassia in qualsiasi momento t sarà -
$$ l_c = \ frac {l_p} {a (t)} $$
$$ l_c = \ int_ {t_1} ^ {t_0} \ frac {cdt} {a (t)} $$
In termini di z,
$$ l_c = \ int_ {t_0} ^ {t_1} \ frac {cdz} {H (z)} $$
Esistono due modi per trovare le distanze, che sono i seguenti:
Rapporto flusso-luminosità
$$ F = \ frac {L} {4 \ pi d ^ 2} $$
dove d è la distanza alla sorgente.
La distanza del diametro angolare di una sorgente
Se conosciamo la dimensione di una sorgente, la sua larghezza angolare ci dirà la sua distanza dall'osservatore.
$$ \ theta = \ frac {D} {l} $$
dove l è la distanza del diametro angolare della sorgente.
θ è la dimensione angolare della sorgente.
D è la dimensione della sorgente.
Considera una galassia di dimensione D e dimensione angolare dθ.
Lo sappiamo,
$$ d \ theta = \ frac {D} {d_A} $$
$$ \ quindi D ^ 2 = a (t) ^ 2 (r ^ 2 d \ theta ^ 2) \ quad \ perché dr ^ 2 = 0; \: d \ phi ^ 2 \ circa 0 $$
$$ \ Rightarrow D = a (t) rd \ theta $$
Mutevole r per rc, la distanza in movimento della galassia, abbiamo -
$$ d \ theta = \ frac {D} {r_ca (t)} $$
Qui, se scegliamo t = t0, finiamo per misurare la distanza attuale dalla galassia. MaDviene misurata al momento dell'emissione del fotone. Pertanto, utilizzandot = t0, otteniamo una distanza maggiore dalla galassia e quindi una sottostima delle sue dimensioni. Pertanto, dovremmo usare il tempot1.
$$ \ quindi d \ theta = \ frac {D} {r_ca (t_1)} $$
Confrontando questo con il risultato precedente, otteniamo:
$$ d_ \ wedge = a (t_1) r_c $$
$$ r_c = l_c = \ frac {d_ \ wedge} {a (t_1)} = d_ \ wedge (1 + z_1) \ quad \ perché 1 + z_1 = \ frac {1} {a (t_1)} $$
Perciò,
$$ d_ \ wedge = \ frac {c} {1 + z_1} \ int_ {0} ^ {z_1} \ frac {dz} {H (z)} $$
dA è la distanza del diametro angolare per l'oggetto.
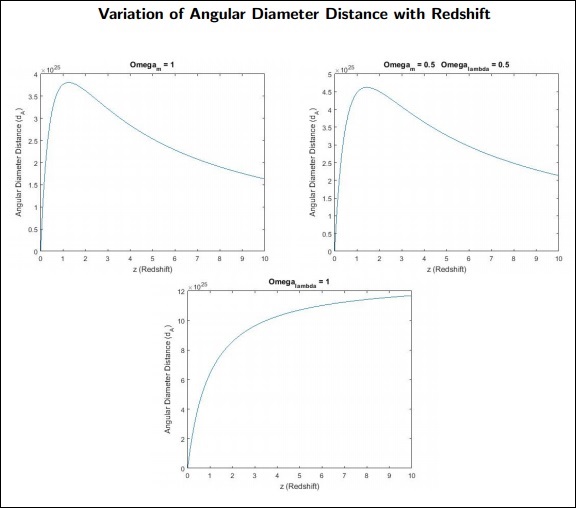
Punti da ricordare
Se conosciamo la dimensione di una sorgente, la sua larghezza angolare ci dirà la sua distanza dall'osservatore.
La distanza corretta è la distanza percorsa dai fotoni dalla sorgente a noi.
La distanza in movimento è la distanza tra gli oggetti in uno spazio che non si espande.
Come discusso nel capitolo precedente, la distanza del diametro angolare da una sorgente allo spostamento verso il rosso z è dato da -
$$ d_ \ wedge (z_ {gal}) = \ frac {c} {1 + z_ {gal}} \ int_ {0} ^ {z_ {gal}} \ frac {1} {H (z)} dz $ $
$$ d_ \ wedge (z_ {gal}) = \ frac {r_c} {1 + z_ {gal}} $$
dove $ r_c $ è la distanza di spostamento.
La distanza di luminosità dipende dalla cosmologia ed è definita come la distanza alla quale il flusso osservato f proviene da un oggetto.
Se la luminosità intrinseca $ d_L $ di un oggetto distante è nota, possiamo calcolarne la luminosità misurando il flusso $ f $ che è determinato da -
$$ d_L (z) = \ sqrt {\ frac {L} {4 \ pi f}} $$
Il Photon Energy diventa rosso spostato.
$$ \ frac {\ lambda_ {obs}} {\ lambda_ {emi}} = \ frac {a_0} {a_e} $$
dove $ \ lambda_ {obs}, \ lambda_ {emi} $ sono osservati e le lunghezze d'onda emesse e $ a_0, a_e $ sono fattori di scala corrispondenti.
$$ \ frac {\ Delta t_ {obs}} {\ Delta t_ {emi}} = \ frac {a_0} {a_e} $$
dove $ \ Delta_t {obs} $ è osservato come l'intervallo di tempo dei fotoni, mentre $ \ Delta_t {emi} $ è l'intervallo di tempo in cui vengono emessi.
$$ L_ {emi} = \ frac {nhv_ {emi}} {\ Delta t_ {emi}} $$
$$ L_ {obs} = \ frac {nhv_ {obs}} {\ Delta t_ {obs}} $$
$ \ Delta t_ {obs} $ impiegherà più tempo di $ \ Delta t_ {emi} $ perché il rilevatore dovrebbe ricevere tutti i fotoni.
$$ L_ {obs} = L_ {emi} \ left (\ frac {a_0} {a_e} \ right) ^ 2 $$
$$ L_ {obs} <L_ {emi} $$
$$ f_ {obs} = \ frac {L_ {obs}} {4 \ pi d_L ^ 2} $$
Per un universo non in espansione, la distanza di luminosità è uguale alla distanza in movimento.
$$ d_L = r_c $$
$$ \ Rightarrow f_ {obs} = \ frac {L_ {obs}} {4 \ pi r_c ^ 2} $$
$$ f_ {obs} = \ frac {L_ {emi}} {4 \ pi r_c ^ 2} \ left (\ frac {a_e} {a_0} \ right) ^ 2 $$
$$ \ Rightarrow d_L = r_c \ left (\ frac {a_0} {a_e} \ right) $$
Stiamo trovando la distanza di luminosità $ d_L $ per calcolare la luminosità dell'oggetto emittente $ L_ {emi} $ -
Interpretation - Se conosciamo il passaggio al rosso zdi qualsiasi galassia, possiamo trovare $ d_A $ e da questo possiamo calcolare $ r_c $. Viene utilizzato per scoprire $ d_L $.
Se $ d_L! = r_c (a_0 / a_e) $, quindi non possiamo trovare Lemi da $ f_ {obs} $.
La relazione tra la distanza di luminosità $ d_L $ e la distanza di diametro angolare $ d_A. $
Sappiamo che -
$$ d_A (z_ {gal}) = \ frac {d_L} {1 + z_ {gal}} \ left (\ frac {a_0} {a_e} \ right) $$
$$ d_L = (1 + z_ {gal}) d_A (z_ {gal}) \ left (\ frac {a_0} {a_e} \ right) $$
Il fattore di scala quando vengono emessi fotoni è dato da -
$$ a_e = \ frac {1} {(1 + z_ {gal})} $$
Il fattore di scala per l'universo attuale è -
$$ a_0 = 1 $$
$$ d_L = (1 + z_ {gal}) ^ 2d_ \ wedge (z_ {gal}) $$
Quale scegliere $ d_L $ o $ d_A $?
Per una galassia di dimensioni note e spostamento verso il rosso per calcolare quanto è grande, viene utilizzato $ d_A $.
Se esiste una galassia di una data grandezza apparente, per scoprire quanto è grande, viene utilizzato $ d_L $.
Example - Se è dato che due galassie di uguale spostamento verso il rosso (z = 1) e nel piano del cielo sono separate da 2.3 arc sec allora qual è la massima separazione fisica tra questi due?
Per questo, usa $ d_A $ come segue:
$$ d_A (z_ {gal}) = \ frac {c} {1 + z_ {gal}} \ int_ {0} ^ {z_ {gal}} \ frac {1} {H (z)} dz $$
dove z = 1 sostituisce H (z) in base ai parametri cosmologici delle galassie.
Punti da ricordare
La distanza di luminosità dipende da cosmology.
Se si conosce la luminosità intrinseca $ d_L $ di un oggetto distante, possiamo calcolarne la luminosità misurando il flusso f.
Per un universo non in espansione, la distanza di luminosità è uguale a comoving distance.
La distanza di luminosità è sempre maggiore di Angular Diameter Distance.
Per ogni spostamento verso il rosso (z), abbiamo due valori per la distanza:
- Distanza diametro angolare (d A )
- Distanza di luminosità (d L )
Non esiste una definizione univoca di distanza "cosmologica" nell'universo. La scelta della distanza dipende dallo scopo e dalla comodità dell'applicazione.
Per testare la tendenza prevista di come la dimensione angolare di un oggetto varia con il redshift, è necessario un metro di misura standard nel cielo. Questo dovrebbe essere un oggetto che:
è molto luminoso, quindi può essere rilevato a z> 1.
è molto grande, in modo da poter risolvere la sua dimensione angolare.
non si è evoluto morfologicamente in un tempo cosmologicamente significativo (z ∼ 1 corrisponde a uno sguardo indietro di circa 7 Gyr).
Alcuni oggetti (come le galassie cD) soddisfano i primi due criteri. Ma quasi ogni oggetto si trova ad evolversi morfologicamente nel tempo. In generale, gli oggetti astrofisici (sorgenti estese) tendono ad essere intrinsecamente più piccoli in passato perché si stanno ancora formando.
Distanza di luminosità
La distanza di luminosità dipende dalla cosmologia. La dipendenza della distanza di luminosità dalla cosmologia la rende una misura utile dei parametri cosmologici.
I parametri cosmologici possono essere stimati se riusciamo a trovare una candela standard che non si evolve intrinsecamente ed esiste dall'universo locale a quello ad alto redshift.
Una candela standard è quella che non differisce nella sua luminosità da sorgente a sorgente. La premessa è che qualsiasi differenza nella luminosità stimata delle candele standard deve essere dovuta alla cosmologia. Una di queste candele è le supernove di tipo Ia.
Tipo 1a Supernovae (SNe)
Questi sono il risultato dell'esplosione di una nana bianca dopo un sufficiente accumulo di massa dalla sua compagna, una gigante rossa o una stella di sequenza principale simile, in un sistema binario. Dopo che il gigante rosso si avvicina alla distanza del lobo di Roche della nana bianca, inizia il trasferimento di massa e alla fine la nana bianca esplode emettendo un'enorme quantità di energia, senza lasciare alcun nucleo dietro. Queste sono chiamate Supernovae di Tipo 1a. Il tasso tipico di esplosione di supernove di tipo 1a in una galassia è di 1 per secolo.
La ricerca del tipo 1a SNe è andata avanti con diverse squadre:
- High z Supernova Search Team (Brian Schmidt, Adam Reiss et al.)
- Supernova Cosmology Project (Saul Perlmutter et al.)
È stato chiamato un altro gruppo di ricerca Carnegie Supernovae Project chi ha dato risultati simili.
La somiglianza dei risultati di diversi team mostra la natura cosmologica del tipo 1a SNe. Quindi, sono candele standard efficienti.
Punti da ricordare
Non esiste una definizione univoca di distanza "cosmologica" nell'universo.
La distanza del diametro angolare e la distanza della luminosità sono le più utilizzate.
Una candela standard è quella che non differisce nella sua luminosità da sorgente a sorgente.
Il tipo 1a SNe soddisfa i criteri per essere una candela standard.
Il CMB (Cosmic Microwave Background) è essenzialmente costituito dai fotoni del tempo in cui materia e radiazione erano in equilibrio. Negli anni '20 l'idea di un universo in espansione fu accettata e poteva rispondere a diverse domande. Ma le domande sull'abbondanza di elementi più pesanti e sull'abbondanza rimasero senza risposta. Inoltre, l'universo in espansione implicava che la densità della materia dovesse diminuire fino a 0.
Nel 1948, George Gammow e Ralph Alpher spiegarono l'origine degli elementi più pesanti e l'abbondanza usando il "Big Bang". Insieme a Robert Herman hanno predetto l'esistenza di "Radiazioni Relittive" o radiazioni rimanenti dal "Big Bang". La temperatura prevista per questa radiazione residua era compresa tra 50-6 K. Nel 1965, Robert Dicke, Jim Peebles e David Wilkinson insieme al gruppo di ricerca di Amo Perizias rilevarono sperimentalmente la CMB.
L'universo primordiale era molto caldo e l'energia era troppo alta perché la materia rimanesse neutra. Quindi, la materia era nella forma ionizzata -Plasma. La Radiazione (fotoni) e la Materia (plasma) hanno interagito principalmente attraverso i seguenti tre processi.
Compton Scattering - (Major Interaction Process) Diffusione anelastica tra fotone ad alta energia e particella carica a bassa energia.
Thomson Scattering - Diffusione elastica del fotone da parte di una particella carica libera.
Inverse Compton Scattering- Particella carica ad alta energia e fotone a bassa energia. Queste interazioni alla fine hanno portato la materia e la radiazione in equilibrio termico.
Equilibrio termale
In equilibrio termico, la radiazione obbedisce al Planck Distribution of Energy,
$$ B_v (T) = \ frac {2hv ^ 3} {c (e ^ {hv / k_BT} -1)} $$
Durante questo periodo, a causa delle interazioni molto frequenti, il percorso libero medio dei fotoni era molto piccolo. L'universo era opaco alle radiazioni. L'universo primordiale era dominato dalle radiazioni. L'universo si è evoluto in modo tale che la materia e la radiazione hanno raggiunto l'equilibrio termico e la loro densità di energia è diventata uguale. Questo può essere visto dal grafico che mostra l'evoluzione della densità con il fattore di scala. Cerchiamo di scoprire il fattore di scala (tempo) (a (t)) in cui la materia e la radiazione hanno raggiunto l'equilibrio.
$$ \ rho_m \ propto \ frac {1} {a ^ 3}, \: \ rho_r \ propto \ frac {1} {a ^ 4} $$
$$ \ frac {\ rho_ {m, t}} {\ rho_ {r, t}} = \ frac {\ Omega_ {m, t}} {\ Omega_ {r, t}} = \ frac {\ Omega_ { m, 0}} {\ Omega_ {r, 0}} a (t) $$
All'equilibrio,
$$ \ frac {\ rho_ {m, t}} {\ rho_ {r, t}} = \ frac {\ Omega_ {m, t}} {\ Omega_ {r, t}} = 1 $$
$$ \ Rightarrow \ frac {\ Omega_ {m, 0}} {\ Omega_ {r, 0}} a (t) = 1 \: \ Rightarrow a (t) = 2.96 \ times 10 ^ {- 4} $$
utilizzando $ \ Omega_ {m, 0} = 0.27 $ e $ \ Omega_ {r, 0} = 8 \ times 10 ^ {- 5} $. Lo spostamento verso il rosso corrispondente a questo fattore di scala è dato da:
$$ z = 1 / a (t) -1 \ circa 3375 $$
La densità di energia della radiazione è diminuita a causa dell'espansione dell'universo. Così l'universo ha iniziato a raffreddarsi. Quando l'energia dei fotoni iniziò a diminuire, iniziarono a formarsi atomi neutri. Così, intorno a un redshift di 1300, iniziò a formarsi l'idrogeno neutro. Questa era aveva una temperatura vicina ai 3000K.
L'interazione tra materia e radiazione divenne molto rara e così l'universo iniziò a diventare trasparente alla radiazione. Questo periodo di tempo è chiamato“Surface of last scattering”poiché il percorso libero medio dei fotoni è diventato molto grande a causa del quale non ha avuto luogo quasi nessuna dispersione dopo questo periodo. È anche chiamato come“Cosmic Photosphere”.
Punti da ricordare
La CMB è costituita dai fotoni dell'epoca in cui materia e radiazione erano in equilibrio.
L'universo primordiale era molto caldo e l'energia era troppo alta perché la materia rimanesse neutra, quindi esisteva come materia-plasma ionizzato.
Compton Scattering, Thomson Scattering, Inverse Compton Scattering erano i 3 processi di interazione materia-radiazione allora.
L'universo si è evoluto in modo tale che la materia e la radiazione hanno raggiunto l'equilibrio termico.
Dobbiamo prima capire cosa caratterizza il decoupling. Sappiamo che le energie erano molto più elevate a tal punto che la materia esisteva solo sotto forma diIonized Particles. Pertanto, in epoche di disaccoppiamento e ricombinazione, l'energia doveva diminuire per consentire la ionizzazione dell'idrogeno. È possibile effettuare un calcolo approssimativo per la stima della temperatura al momento del disaccoppiamento.
Questo è stato eseguito come segue:
Innanzitutto, considera solo la ionizzazione dell'idrogeno allo stato fondamentale.
$$ hv \ circa k_BT $$
$$ \ quindi T \ approx \ frac {hv} {k_B} $$
Per la ionizzazione dell'idrogeno allo stato fondamentale, hν è 13,6 eV e kB è il Boltzmann Constant8,61 × 10 −5 eV / K che rivela che la temperatura è 1,5 × 105 kelvin.
Questo essenzialmente ci dice che se la temperatura è inferiore a 1,5 × 10 5 K, gli atomi neutri possono iniziare a formarsi.
Sappiamo che il rapporto tra fotoni e barioni è di circa 5 × 10 10 . Quindi anche alla fine del grafico, dove il numero di fotoni si riduce, ci saranno ancora fotoni sufficienti per ionizzare gli atomi di idrogeno. Inoltre, la ricombinazione di elettroni e protoni non garantisce un atomo di idrogeno allo stato fondamentale. Gli stati eccitati richiedono minore energia per la ionizzazione. Quindi un'analisi statistica disciplinata dovrebbe essere eseguita caso per caso per ottenere un valore accurato. I calcoli impostano la temperatura intorno ai 3000 K.
Per ragioni di spiegazione, consideriamo il caso dell'eccitazione dell'idrogeno nel primo stato eccitato. L'espressione generale per il rapporto tra il numero di fotoni con energia maggiore diΔE, Nγ (> ΔE) al numero totale di fotoni Nγ è dato da -
$$ \ frac {N_ \ gamma (> \ Delta E)} {N_ \ gamma} \ propto e ^ {\ frac {- \ Delta E} {kT}} $$
Per il caso di eccitazione dell'idrogeno al primo stato eccitato, ΔEè 10,2 eV. Ora, se consideriamo un numero altamente conservativo di almeno 1 fotone con energia maggiore di 10,2 per ogni barione (tenendo presente che il rapporto è 5 × 10 10 , otteniamo la temperatura dall'equazione 3 come 4800 K (Nγ inserito (> ΔE) = Np).
Questa è la temperatura per creare una popolazione di atomi di idrogeno neutri nel primo stato eccitato. La temperatura per ionizzare questo è significativamente inferiore. Pertanto, otteniamo una stima migliore di 1,5 × 10 5 K che è più vicina al valore accettato di 3000 K.
Redshift - Rapporto di temperatura
Per comprendere la relazione tra spostamento verso il rosso e temperatura, utilizziamo i due metodi seguenti come descritto di seguito.
Metodo 1
A partire dal Wien’s Law, lo sappiamo
$$ \ lambda_mT = costante $$
Per mettere in relazione questo con il redshift, usiamo:
$$ 1 + z = \ frac {\ lambda_0} {\ lambda_e} $$
Come $ λ_oT_o = λ_eT (z) $, otteniamo -
$$ T (z) = T_0 \ frac {\ lambda_0} {\ lambda_e} = T_0 (1 + z) $$
Ambientazione To come valore corrente 3K, possiamo ottenere valori di temperatura per un dato spostamento verso il rosso.
Metodo 2
In termini di frequenza, sappiamo -
$$ v_0 = \ frac {v_e} {1 + z} $$
$$ B_vdv = \ frac {2hv ^ 3} {c ^ 2} \ frac {dv} {e ^ {hv / kT} -1} $$
Questo ci dice sull'energia netta dei fotoni per un intervallo di energia e hνè l'energia di un singolo fotone. Quindi, possiamo ottenere il numero di fotoni diBνdν/hν.
Se $ n_ {νo} $ è per presente e $ n_ {νe} $ per emesso, otteniamo -
$$ \ frac {n_ {v_e}} {n_ {v_0}} = (1 + z) ^ 3 $$
Sulla semplificazione, otteniamo,
$$ n_ {v_0} = \ frac {2v_c ^ 2} {c ^ 2} \ frac {dv_c} {e ^ {hv / kT} -1} \ frac {1} {(1 + z) ^ 3} = \ frac {2v_0 ^ 2} {c ^ 2} \ frac {dv_c} {e ^ {hv / kT} -1} $$
Questo ci dà il Wien’s Law di nuovo e quindi si può concludere che -
$$ T (z) = T_0 \ frac {\ lambda_0} {\ lambda_e} = T_0 (1 + z) $$
Punti da ricordare
- L'universo primordiale era molto caldo, ∼ 3000K.
- Le misurazioni attuali rivelano che la temperatura dell'universo è vicina a 3K.
- Più si va indietro nel tempo, la temperatura aumenta proporzionalmente.
In questo capitolo discuteremo l'anisotropia della radiazione CMB e del COBE, ovvero Cosmic Background Explorer.
Anisotropie primarie nella CMB
Per comprendere le osservazioni dallo spazio e le anisotropie primarie nella radiazione di fondo a microonde cosmiche, prendiamo le seguenti equazioni e comprendiamole come mostrato di seguito.
Densità del numero di fotoni CMB (n γ , 0)
$$ n _ {\ gamma, 0} = \ frac {Totale \: energia \: densità} {Caratteristica \: energia \: di \: fotoni} $$
$$ n _ {\ gamma, 0} = \ frac {aT_0 ^ 4} {k_BT_0} $$
Dove si trova $ k_B $ Boltzmann Constant e $ T_0 $ è il file present temperature of the universe.
Usando la temperatura attuale $ (T_0) $ come 2,7 K, otteniamo la densità del numero di fotoni CMB corrente come 400 cm -3 .
La densità del numero di fotoni stellari cosmici è molto più piccola (∼ = 10 −3 cm −3 ) su grandi scale.
Rapporto barione / fotone (η)
Se i contributi stellari delle galassie, che si mescolano con CMB, sono trascurabili, il rapporto barione / protone è -
$$ \ eta = \ frac {n_ {b, 0}} {n _ {\ gamma, 0}} $$
Il valore attuale è ∼5 × 10 −10 . Poiché sia la densità del numero di fotone che quella barionica sono proporzionali aa−3, poi η non si evolve con il tempo.
Densita 'energia
Al contrario della densità numerica, la densità energetica della materia è attualmente più dominata della densità energetica dei fotoni.
La densità di energia della materia barionica = $ \ rho_ {b, 0} c ^ 2 = 0,04 \ rho_cc ^ 2 = 2 × 10 ^ {- 9} ergcm ^ {- 3} $. Mentre, la densità energetica della radiazione = $ aT_0 ^ 4 = 4 \ volte 10 ^ {- 13} ergcm {−3} $.
Isotropia della radiazione CMB
Penzias e Wilsontrovato che il CMB è isotropo entro i limiti delle osservazioni. I limiti sono la bassa risoluzione angolare e la sensibilità degli strumenti. Hanno fatto osservazioni dalla terra, per questo motivo, le osservazioni non possono essere effettuate attraverso tutto lo spettro poiché il vapore acqueo nell'atmosfera assorbe molte lunghezze d'onda che vanno da 1 mm a 1 m. Quindi, CMB non può essere affermato come uno spettro.
Si ritiene che il CMB sia invariante dal punto di vista della rotazione (isotropo). Poiché esisteva un tempo in cui materia e radiazione erano in equilibrio, la formazione delle strutture nell'universo è inspiegabile. Poiché la distribuzione della materia non è isotropa ma è aggregata come una rete cosmica con enormi vuoti in mezzo, si pensa che CMB abbia un'origine extragalattica.
Ma, quando sono iniziate le osservazioni dallo spazio, sono state trovate anisotropie nella CMB, il che ha portato al ragionamento che queste anisotropie nella materia portano alla formazione di strutture.
Osservazione della radiazione CMB dallo spazio
I principali satelliti lanciati per osservare la CMB sono stati:
Cosmic Microwave Background Explorer (COBE, 1989)
Wilkinson Microwave Anisotropy Probe (WMAP, 2001) e
Planck (2009).
COBE (Cosmic Background Explorer)
COBE aveva principalmente due strumenti. Li avevamoFar InfraRed Absolute Spectrometer (FIRAS) e Differential Microwave Radiometers(Antenne DMR). FIRAS misura l'intensità del CMB in funzione della lunghezza d'onda lungo una qualsiasi direzione specifica. Considerando che, DMR ha 3 antenne per misurare la differenza di intensità di CMB da tre diverse direzioni. I seguenti suggerimenti ci forniscono ulteriori informazioni su FIRAS e DMR.
Le osservazioni CMB di FIRAS mostrano che la radiazione CMB corrisponde allo spettro del corpo nero a T = 2,72528 ± 0,00065 K.
Il DMR misura tre frequenze (31,5 GHz, 53 GHz, 90 GHz) in tutte le direzioni nel cielo.
Il "simbolo di batman rosso" nelle osservazioni DMR è il rumore dall'emissione in primo piano (emissione di sincrotrone diffusa galattica).
Le variazioni di intensità nelle osservazioni corrispondono alle variazioni di temperatura. La presenza di punti caldi e freddi dimostra che la radiazione CMB è anisotropa.
Questa anisotropia deve essere presente al momento del disaccoppiamento poiché non ci sono distorsioni in CMB. Quindi, la materia dovrebbe avere alcune sacche con una densità maggiore di quella delle altre.
Risultati COBE
Lo spettro CMB (intensità in funzione dell'energia) è quasi un corpo nero perfetto corrispondente a T = 2,7 K. L'intensità specifica della radiazione CMB è quasi la stessa per tutte le direzioni. La conferma che l'universo è isotropo su larga scala (convalida la nostra ipotesi di principio cosmologico).
L'analisi dei dati ha mostrato che ci sono anisotropie di temperatura ("fluttuazioni") nello spettro CMB alla risoluzione di COBE (DMR).
Resolution of COBE, WMAP, Planck
Lo strumento DMR a bordo del COBE aveva una risoluzione spaziale limitante (massima) di ∼ 7 gradi.
Wilkinson Microwave Anisotropy Probe (WMAP) aveva una risoluzione media di ∼ 0,7 gradi.
Il satellite Planck ha una risoluzione angolare di ∼ 10 minuti d'arco.
Punti da ricordare
La densità del numero di fotoni stellari cosmici è molto più piccola della densità del numero di fotoni CMB.
Viviamo in un universo dominato dalla materia, poiché la densità di energia della materia è superiore alla densità di energia del fotone.
COBE, WMAP, Planck sono sforzi per misurare e quantificare le anisotropie nella CMB.
La formazione della struttura nell'universo è il risultato delle anisotropie CMB.
Quando guardiamo la mappa CMB del cielo ottimizzata e corretta, c'è molta contaminazione in primo piano, che è una sorta di anisotropyin queste mappe. Possiamo vedere che queste emissioni in primo piano provengono dalla galassia della Via Lattea. L'intensità della CMB è alta lungo il piano del piano galattico e si riduce man mano che ci allontaniamo. In questi possiamo osservare le anisotropie secondarie, che sono emissioni di sincrotrone dalla galassia. Queste emissioni costituiscono la contaminazione in primo piano. Per osservare l'emissione di CMB dal cielo, dobbiamo sottrarre queste emissioni in primo piano.
L'immagine seguente mostra la CMB con le emissioni in primo piano.

Anisotropia dipolare
C'è un altro tipo di anisotropia, che è stata trovata nella mappa di tutto il cielo CMB, è chiamata anisotropia dipolare. Non è associato all'universo primordiale. Questo può essere rappresentato usando funzioni armoniche sferiche. Se c'è un pattern su una superficie sferica e vogliamo mapparlo usando funzioni matematiche, possiamo farlo usando funzioni trigonometriche. Quindi, quando mappiamo, può essere un monopolo - lo stesso in ogni direzione, o un dipolo - capovolge le proprietà quando viene ruotato di 180 gradi. Allo stesso modo, abbiamo il quadrupolo e così via. Per uno schema complesso, può essere espresso come la somma di questi unipolo, dipolo, quadrupolo, ecc.
La CMB è modellata in modo tale che una delle principali fonti di anisotropia nella mappa di tutto il cielo è questa anisotropia dipolare, ma non è un modello primordiale di CMB. Questo può essere visto nell'immagine qui sotto.

La direzione del dipolo che vediamo non è una direzione casuale. L'anisotropia dipolare ha una direzione. Vediamo l'intensità CMB lungo una direzione specifica. Questa direzione è dovuta al vettore di velocità del sistema solare. La velocità della Terra può essere rappresentata rispetto al Sole o al centro della galassia. La direzione in cui si sta muovendo la terra, osserviamo un Blueshift e Redshift e il dipolo si trova lungo questa direzione.
L'immagine sopra ha un tipico aspetto di dipolo perché la nostra galassia si sta muovendo in una direzione specifica. Il risultato è: un lato del cielo apparirà spostato verso il rosso e l'altro lato del cielo apparirà spostato verso il blu. In questo caso, Redshifting significa che i fotoni sono più lunghi in lunghezza d'onda = più freddi (quindi al contrario del loro nome, appaiono blu nel diagramma sopra).
Possiamo dire che la terra si sta muovendo in una direzione specifica rispetto al sole / centro galattico / CMB nel cielo in un dato istante. Quindi, se guardiamo a qualsiasi angolo e misuriamo la temperatura per CMB, sarebbe diverso. Questo perché stiamo misurando fotoni che sono Blueshift o Redshift e dipendono dalla linea di vista dei fotoni nel cielo.
Punti da ricordare
La contaminazione in primo piano nella mappa di tutto il cielo CMB è chiamata anisotropia di CMB.
Queste emissioni provengono dalla nostra galassia della Via Lattea.
I 2 tipi di anisotropia sono: anisotropia dipolare e anisotropia dello spettro di potenza angolare.
L'anisotropia del dipolo è in una direzione specifica, mentre l'anisotropia dello spettro di potenza angolare è diffusa ovunque.
La lunghezza dell'orizzonte è la distanza percorsa dai fotoni luminosi da "The Big Bang" a "The Recombination Era". Il 1 ° picco dello spettro angolare è a θ = 1◦ (l = 180), che è una scala molto speciale lunghezza.
La distanza corretta tra due punti è data da:
$$ r_p = \ int_ {0} ^ {t} cdt $$
Quando prendiamo l'intervallo di tempo da t = 0 a t = t rec , allora
$$ r_H = \ int_ {0} ^ {t_ {rec}} cdt $$
Dove $ r_H $ è la corretta distanza dell'orizzonte.
Ora sappiamo che -
$$ \ dot {a} = \ frac {\ mathrm {d} a} {\ mathrm {d} t} $$
$$ dt = \ frac {da} {\ dot {a}} $$
Quando t = 0, a = 0.
Quindi $ t = t_ {rec}, a = a_0 / (1 + z_ {rec}) $.
Quindi, possiamo scrivere,
$$ r_H (z_ {rec}) = \ int_ {0} ^ {a_ {rec}} c \ frac {da} {aH} $$
$$ H (a_ {rec}) = H (z_ {rec}) = H_0 \ sqrt {\ Omega_ {m, 0}} a ^ {- 3/2} $$
Durante Recombination period universeera la materia dominata. cioèΩrad << Ωmatter. Pertanto, il termine radiazione viene eliminato.
$$ r_H (z_ {rec}) = \ frac {c} {H_0 \ sqrt {\ Omega_ {m, 0}}} \ int_ {0} ^ {a_ {rec}} \ frac {da} {a ^ { -1/2}} $$
$$ r_H (z_ {rec}) = \ frac {2c} {3H_0 \ sqrt {\ Omega_ {m, 0}}} \ frac {1} {(1 + z_ {rec}) ^ {3/2}} $$
$$ \ theta_H (rec) = \ frac {r_H (z_ {rec})} {d_A (z_ {rec})} $$
Che è uguale a 0,5 gradi, se mettiamo tutti i valori noti nell'equazione.
Il Electromagnetic radiationè opaco dalla superficie dell'ultima dispersione. Qualsiasi due punti "non" che si trovano nell'orizzonte l'uno dell'altro non devono necessariamente avere le stesse proprietà. Quindi, darà diversi valori di temperatura.
Possiamo ottenere due punti su questa superficie che non si intersecano tra loro, il che significa che in un punto l'universo si è espanso più velocemente della velocità della luce che è il modello inflazionistico di espansione.
Punti da ricordare
La lunghezza dell'orizzonte è la distanza percorsa dai fotoni della luce da "The Big Bang" a "The Recombination Era".
Durante il periodo di ricombinazione, l'universo era dominato dalla materia.
La radiazione elettromagnetica è opaca dalla superficie dell'ultima dispersione.
Astrobiologyè lo studio dell'origine, evoluzione, distribuzione e futuro della vita nell'universo. Si occupa di scoprire e rilevareExtrasolar Planets.
Astrobiology affronta i seguenti punti:
Come inizia ed evolve la vita? (biologia + geologia + chimica + scienze atmosferiche)
Ci sono mondi oltre la terra che sono favorevoli alla vita? (astronomia)
Quale sarebbe il futuro della vita sulla terra?
Astronomy affronta i seguenti punti:
Come rilevare il sistema planetario attorno ad altre stelle?
Uno dei metodi è l'imaging diretto, ma è un compito molto difficile perché i pianeti sono sorgenti di luce estremamente deboli rispetto alle stelle e quella poca luce che proviene da essi tende a perdersi nel bagliore della loro stella madre.
Il contrasto è migliore quando il pianeta è più vicino alla sua stella madre ed è caldo, in modo che emetta un'intensa radiazione infrarossa. Possiamo realizzare immagini nella regione degli infrarossi.
Tecniche per la rilevazione di pianeti extrasolari
Le tecniche più efficienti per il rilevamento dei pianeti extrasolari sono le seguenti. Ciascuno di questi è spiegato in dettaglio anche nei capitoli successivi.
Metodo della velocità radiale
È anche chiamato metodo Doppler. In questo -
Il sistema dei pianeti stellari ruota attorno al loro baricentro, la stella oscilla.
L'oscillazione può essere rilevata da
Turni periodici rosso / blu. Astrometria: misurazione molto precisa degli oggetti nel cielo.
Metodo di transito
Il metodo di transito (telescopio spaziale Kepler) viene utilizzato per determinare le dimensioni. Il calo di luminosità di una stella per pianeta è solitamente molto inferiore, a differenza di un sistema binario.
Imaging diretto
Immaginare il pianeta usando un telescopio.
Diamo un'occhiata a un caso di studio condotto sul metodo della velocità radiale.
Argomento di studio
Questo caso di studio è sull'orbita circolare e sul piano dell'orbita perpendicolare al piano del cielo. Il tempo impiegato da entrambi intorno al baricentro sarà lo stesso. Sarà uguale alla differenza di orario tra due Redshift o Blueshift.
Considera l'immagine seguente.

In A e C viene misurata la piena velocità. In C, la velocità è zero.
Vrmax = V * è la vera velocità della stella.
P è il periodo di tempo della stella e del pianeta.
θ è la fase dell'orbita.
Star Mass - M * , raggio orbitale a * , massa planetariamp.
Dall'equazione del centro di massa,
$$ m_p a_p = M_ \ ast a_ \ ast $$
Dall'equazione della velocità,
$$ V_ \ ast = \ frac {2 \ pi a_ \ ast} {P} $$
$$ \ Rightarrow a_ \ ast = \ frac {PV_ \ ast} {2 \ pi} $$
A partire dal Kepler’s Law,
$$ P ^ 2 = \ frac {4 \ pi ^ 2a_p ^ 3} {GM_ \ ast} $$
$$ \ Rightarrow a_p = \ left (\ frac {P ^ 2GM_ \ ast} {4 \ pi ^ 2} \ right) ^ {1/3} $$
Dalle equazioni precedenti, otteniamo:
$$ \ Rightarrow m_p = \ left (\ frac {P} {2 \ pi G} \ right) ^ {1/3} M_ \ ast ^ {2/3} V_ \ ast $$
Otteniamo: $ m_p, a_p $ e $ a_ \ ast $.
L'equazione di cui sopra è orientata verso la maggior parte dei pianeti massicci vicini alla stella.
Punti da ricordare
L'astrobiologia è lo studio dell'origine, dell'evoluzione, della distribuzione e del futuro della vita nell'universo.
Le tecniche per rilevare i pianeti extrasolari sono: metodo della velocità radiale, metodo di transito, imaging diretto, ecc.
Le oscillazioni possono essere rilevate da periodici spostamenti rosso / blu e dall'astrometria.
Il metodo della velocità radiale è orientato al rilevamento di pianeti massicci vicini alla stella.
Nel capitolo precedente, il metodo della velocità radiale per il caso in cui il piano orbitale e il piano del cielo sono perpendicolari è stato discusso per le orbite circolari. Qui, ci occupiamo di un altro caso, quando il piano orbitale e il piano del cielo non sono perpendicolari per orbite circolari.
Quando il piano orbitale è ad angolo rispetto al piano del cielo (non perpendicolare), abbiamo la seguente situazione:

In questo caso, quando erano perpendicolari, avevamo due punti in cui potevamo misurare la velocità reale. Ma qui non è possibile. In tutti i punti, possiamo misurare solo una componente della velocità reale,v.
$$ v_r = v \: sin (i) cos (\ theta) $$
dove θè la fase dell'orbita che è una quantità dipendente dal tempo. L'angolo di inclinazioneid'altra parte, è indipendente dal tempo. Quindi,
$$ (v_r) _ {max} = v \: sin (i) $$
La curva di velocità radiale osservata sarà della seguente forma:

Quando il piano orbitale è perpendicolare al cielo -
$$ m_p = \ left (\ frac {P} {2 \ pi G} \ right) ^ {\ frac {1} {3}} (M_ \ ast) ^ {\ frac {2} {3}} v $ $
dove mp, P, G, M∗sono rispettivamente la massa del pianeta, il periodo orbitale, la costante gravitazionale universale e la massa della stella. Ma in questo caso, dovremmo modificarlo come segue:
$$ m_psin (i) = \ left (\ frac {P} {2 \ pi G} \ right) ^ {\ frac {1} {3}} (M_ \ ast) ^ {\ frac {2} {3} } (v_r) _ {max} $$
Ma trovare il valore di i è un compito difficile. Possiamo imporre alcuni vincoli al valore diiutilizzando il metodo di transito. Il passaggio del pianeta tra la stella e la Terra è chiamato transito. Possiamo ottenere la curva di luce osservando un transito e un calo significativo nel flusso osservato di una curva di luce implica che i è vicino a 90 gradi. Se tali condizioni non sono soddisfatte, non possiamo avere alcuna idea sul valore dii. Quindi il valore dimp che troviamo può servire come limite inferiore per la massa del pianeta, poiché in realtà lo è mp sin(i) e sin(i) ≤ 1.
Per concludere, il metodo della velocità radiale è più conveniente del metodo di transito perché la velocità radiale può essere misurata in qualsiasi momento, ma le misurazioni di transito possono essere effettuate solo durante il transito che potrebbe non durare a lungo.
Punti da ricordare
La ricerca dell'inclinazione dell'orbita del pianeta non si ottiene con il metodo della velocità radiale.
Il metodo della velocità radiale è migliore del metodo di transito perché la velocità radiale può essere misurata sempre a differenza dei transiti.
I transiti sono di breve durata e molto facili da perdere.
Il metodo di transito (Kepler Space Telescope)viene utilizzato per scoprire la dimensione. Il calo di luminosità di una stella da parte di un pianeta è solitamente molto meno diverso da un sistema binario.
F0 è il flusso della stella prima che il pianeta la occulti.
F1 è il flusso dopo che l'intero pianeta è di fronte alla stella.
L'immagine seguente verrà utilizzata per tutti i calcoli.

$$ \ frac {F_0 - F_1} {F_0} = \ frac {\ pi r_p ^ {2}} {\ pi R ^ 2_ \ ast} $$
$$ \ frac {\ Delta F} {F} \ cong \ frac {r ^ 2_p} {R ^ 2_ \ ast} $$
$$ \ left (\ frac {\ Delta F} {F} \ right) _ {earth} \ cong 0.001 \% $$
$$ \ left (\ frac {\ Delta F} {F} \ right) _ {jupiter} \ cong 1 \% $$
Questo non è facile da ottenere con un telescopio a terra. È ottenuto dal telescopio Hubble.

Qui $ t_T $ è il tempo tra la posizione A e D e $ t_F $ è il tempo tra la posizione B e C.
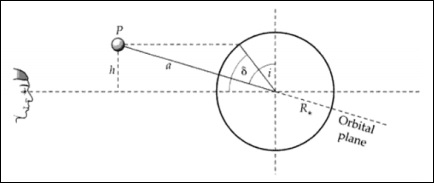
La geometria di un transito in relazione all'inclinazione idel sistema. La latitudine e l'inclinazione di transito sono intercambiabili.
Dalle immagini sopra, possiamo scrivere:
$$ \ frac {h} {a} = cos (i) $$
$$ \ frac {h} {R_ \ ast} = sin (\ delta) $$
$$ cos (i) = \ frac {R_ \ ast sin (\ delta)} {a} $$
$$ y ^ 2 = (R_ \ ast + R_p) ^ 2 - h ^ 2 $$
$$ y = [(R_ \ ast + R_p) ^ 2 - h ^ 2] ^ {\ frac {1} {2}} $$
$$ sin (\ theta) = \ frac {y} {a} $$
$$ \ theta = sin ^ {- 1} \ left [\ frac {(R_ \ ast + R_p) ^ 2 - a ^ 2cos ^ 2 (i)} {a ^ 2} \ right] ^ {\ frac {1 } {2}} $$
$$ t_T = \ frac {P} {2 \ pi} \ times 2 \ theta $$
Qui, $ t_T $ è la frazione di un periodo di tempo per il quale avviene il transito e (2θ / 2π) è la frazione dell'angolo per il quale avviene il transito.
$$ sin (\ frac {t_T \ pi} {P}) = \ frac {R_ \ ast} {a} \ left [\ left (1+ \ frac {R_p} {R_ \ ast} \ right) ^ 2 - \ left (\ frac {a} {R_ \ ast} cos (i) \ right) ^ 2 \ right] ^ {\ frac {1} {2}} $$
Di solito, un >> R ∗ >> Rp. Quindi, possiamo scrivere -
$$ sin (\ frac {t_T \ pi} {P}) = \ frac {R_ \ ast} {a} \ left [1- \ left (\ frac {a} {R_ \ ast} cos (i) \ right ) ^ 2 \ right] ^ {\ frac {1} {2}} $$
Qui, Pè la durata tra due transiti successivi. Il tempo di transito è molto inferiore rispetto al periodo di tempo orbitale. Quindi,
$$ t_T = \ frac {P} {\ pi} \ left [\ left (\ frac {R_ \ ast} {a} \ right) ^ 2 - cos ^ 2 (i) \ right] ^ {\ frac {1 } {2}} $$
Qui, tT, P, R∗ sono gli osservabili, a e i dovrebbe essere scoperto.
Adesso,
$$ sin (\ frac {t_F \ pi} {P}) = \ frac {R_ \ ast} {a} \ left [\ left (1 - \ frac {R_p} {R_ \ ast} \ right) ^ 2 - \ left (\ frac {a} {R_ \ ast} cos \: i \ right) ^ 2 \ right] ^ {\ frac {1} {2}} $$
dove $ y ^ 2 = (R_ \ ast - R_p) ^ 2 - h ^ 2 $.
Permettere,
$$ \ frac {\ Delta F} {F} = D = \ left (\ frac {R_p} {R_ \ ast} \ right) ^ 2 $$
Ora possiamo esprimere,
$$ \ frac {a} {R_ \ ast} = \ frac {2P} {\ pi} D ^ {\ frac {1} {4}} (t ^ 2_T - t ^ 2_F) ^ {- \ frac {1 } {2}} $$
Per le stelle della sequenza principale,
$$ R_ \ ast \ propto M ^ \ alpha_ \ ast $$
$$ \ frac {R_ \ ast} {R_0} \ propto \ left (\ frac {M_ \ ast} {M_0} \ right) ^ \ alpha $$
Questo da R∗.
Quindi, otteniamo anche il valore di "a".
Quindi, otteniamo "R p ", "ap" e anche "i".
Per tutto questo
$$ h \ leq R_ \ ast + R_p $$
$$ a \: cos \: i \ leq R_ \ ast + R_p $$
Anche per ~ 89 gradi, la durata del transito è molto ridotta. Il pianeta deve essere molto vicino per ottenere un tempo di transito sufficiente. Questo dà uno stretto vincolo su "i". Una volta ottenuto "i", possiamo derivare "m p " dalla misurazione della velocità radiale.
Questo rilevamento mediante il metodo di transito è chiamato rilevamento casuale, ovvero probabilità di osservare un transito. Di seguito sono riportati i calcoli della probabilità di transito (probabilità di osservazione).
La probabilità di transito è correlata all'angolo solido tracciato dalle due configurazioni di transito estreme, che è:
$$ Solido \: angolo \: di \: pianeta \: = 2 \ pi \ sinistra (\ frac {2R_ \ ast} {a} \ destra) $$
Così come l'angolo solido totale su un semiasse maggiore a, o -
$$ Solido \: angolo \: di \: sfera \: = \: 4 \ pi $$
La probabilità è il rapporto tra queste due aree:
$$ = \: \ frac {area \: di \: cielo \: coperto \: da \: favorevole \: orientamento} {area \: di \: cielo \: coperto \: da \: tutto \: possibile \: orientamento \: di \: orbita} $$
$ = \ frac {4 \ pi a_pR_ \ ast} {4 \ pi a ^ 2_p} = \ frac {R_ \ ast} {a_p} $ $ \ frac {area \: of \: hollow \: cyclinder} {area \ : di \: sfera} $
Questa probabilità è indipendente dall'osservatore.
Punti da ricordare
- Il metodo di transito (Kepler Space Telescope) viene utilizzato per scoprire le dimensioni.
- Il rilevamento tramite metodo di transito è un rilevamento casuale.
- Il pianeta deve essere molto vicino per ottenere un tempo di transito sufficiente.
- La probabilità di transito è correlata all'angolo solido del pianeta.
- Questa probabilità è indipendente dal sistema di riferimento dell'osservatore.
La prima immagine diretta di un pianeta extrasolare, nel 2004, era di un pianeta di massa 3-10 Mjupiter in orbita attorno a una nana bruna (2M1207) con una massa di 25 Mjupiter. Tecniche come velocità radiale, transito, microlensing gravitazionale, imaging, astrometria, ecc., Sono state utilizzate per il rilevamento di esopianeti. Il numero di rilevamenti aumenta ogni anno.
Fino al 2010 circa, il metodo della velocità radiale era ampiamente utilizzato, ma ora la maggior parte dei rilevamenti viene eseguita con il metodo di transito. C'è stato un picco nel numero di rilevamenti nel 2014, ovvero quandoKepler Space Telescope (KST) ha iniziato a dare i risultati.
Una distribuzione di periodo di massa mostra che il metodo della velocità radiale è più polarizzato verso il rilevamento di pianeti massicci con un periodo più ampio, mentre utilizzando il metodo di transito, i pianeti con periodo inferiore vengono rilevati solo come mostrato nell'immagine seguente (Cortesia: NASA Exoplanet Archive) .
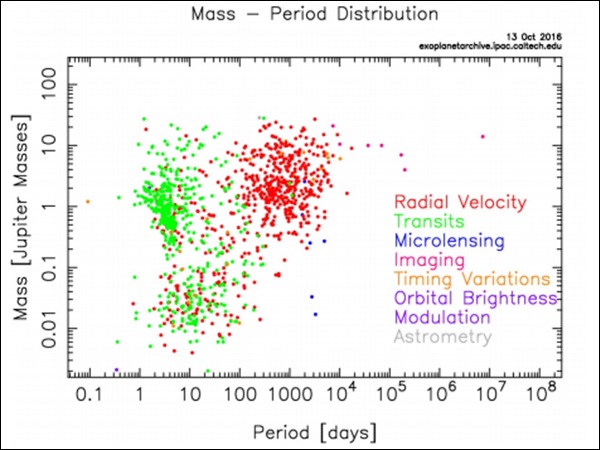
Dall'avvento del KST c'è un aumento colossale nel numero di rilevamenti di pianeti di massa più piccoli. Ciò è evidente dalla figura sotto riportata. I pianeti rilevati da KST sono divisi in due gruppi: pianeti massicci chiamati "Giove Caldi" e pianeti di massa inferiore chiamati "Super Terre Calde" (poiché sono più massicci della Terra).

Quando tracciamo il numero di pianeti extrasolari rilevati rispetto alla distanza da essi, scopriamo che la maggior parte di questi pianeti si trova entro 2kpc, che è ben all'interno della nostra galassia. Forse i pianeti non sono così rari nell'universo, poiché la nostra rilevazione è limitata solo a certi tipi di pianeti in una parte molto piccola dell'universo.
I pianeti sono formati da circumstellar disc o proto planetary disc. Se i pianeti si formano come sottoprodotto durante la formazione stellare, forse il numero di pianeti nell'universo supera il numero di stelle nell'universo !!
Zone abitabili
Una Zona Abitabile può essere definita come la zona intorno alla stella dove l'acqua può esistere nella sua forma liquida. Considera un pianeta a distanza $ a_p $ dalla stella come mostrato nella figura seguente. Di seguito viene descritto un metodo semplice per calcolare la temperatura del pianeta.
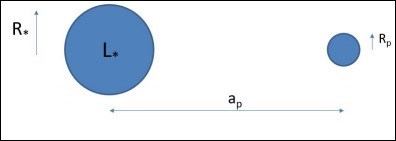
$$ \ left (\ frac {L_ \ ast} {4 \ pi a ^ 2_p} \ right) \ pi R ^ 2_p (1 - A) = 4 \ pi R ^ 2_p \ sigma T ^ 4_p $$
e
$$ \ frac {L_ \ ast} {4 \ pi R ^ 2_ \ ast} = \ sigma T ^ 4_ \ ast $$
$$ \ quindi T_p = (1 - A) T_ \ ast \ sqrt {\ frac {R_ \ ast} {2a_p}} $$
Nel nostro caso la sostituzione
Lsun = 3.83 x 1026
ap = 1.5 ∗ 1011 and
A = 0.3
Darà $ T_ {Earth} = 255K $. Il calcolo effettivo è molto complesso e include la fisica delle nuvole. La zona abitabile nel nostro sistema solare è compresa tra 0,9 UA e 1,7 UA.
Si è scoperto che la luminosità del Sole aumenta con il tempo a causa della diminuzione della pressione del gas. Era il 30% meno luminoso quando ha iniziato a bruciare idrogeno. Ciò risulterebbe in uno spostamento della zona abitabile lontano dal sole. Poiché la Terra è vicino al bordo interno della Zona Abitabile, forse un giorno uscirà dalla zona!
Zona continuamente abitabile
In breve è definito come CHZpuò essere definita come la regione in cui l'acqua liquida può esistere durante l'intera vita della sequenza principale di una stella. Il KST ha rilevato molti pianeti extrasolari che si trovano nella zona abitabile.
Una firma biologica è qualsiasi sostanza, come un elemento, un isotopo, una molecola o un fenomeno che fornisce prove scientifiche della vita passata o presente. Un esempio è il rilevamento sia di O 2 che di CO 2 su un pianeta, che di solito non è possibile solo attraverso processi geologici. Questa rilevazione viene eseguita analizzando gli spettri di assorbimento.
Punti da ricordare
Tecniche come velocità radiale, transito, microlensing gravitazionale, imaging, astrometria, ecc., Sono state utilizzate per il rilevamento di esopianeti.
Il metodo della velocità radiale è più orientato al rilevamento di pianeti massicci con un periodo più ampio.
I pianeti massicci caldi sono chiamati "Giove caldo" e i pianeti di massa inferiore sono chiamati "Super Terre calde".
Il numero di pianeti nell'universo supera il numero di stelle nell'universo.
Una zona abitabile può essere definita come la zona intorno alla stella dove l'acqua può esistere nella sua forma liquida.