デジタル回路-しきい値ロジック
前の章では、論理ゲートを使用してさまざまな組み合わせ回路を実装しました。NOTゲートを除いて、残りのすべての論理ゲートには少なくとも2つの入力と1つの出力があります。同様に、threshold gate また、少なくとも1つの入力と1つの出力のみが含まれます。
さらに、各入力に対するそれぞれの重みとしきい値が含まれています。これらの重みとしきい値の値は、任意の有限の実数にすることができます。
スレッショルドゲートの基本
しきい値ゲートの入力はXですしてみましょう1、X 2、X 3、...、X nは。これらの入力の対応する重みは、Wである1、W 2、W 3、...、W N。ザ・symbol 次の図に、しきい値ゲートの値を示します。
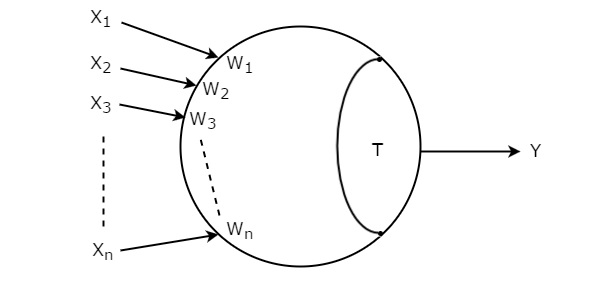
Threshold gate円で表され、それはX「n」の入力を有している1 XにNと単一出力、Y.この円は二つの部分に形成されています。1つの部分は入力に対応する重みを表し、他の部分はしきい値Tを表します。
対応する重みを持つ入力の積の合計は、次のように知られています。 weighted sum。この加重和がしきい値T以上の場合、出力Yのみが1に等しくなります。それ以外の場合、出力Yはゼロに等しくなります。
Mathematically、スレッショルドゲートの入力と出力の関係は次のように書くことができます。
$$ Y = 1、\の場合:\:W_ {1} X_ {1} + W_ {2} X_ {2} + W_ {3} X_ {3} + ... W_ {n} X_ {n} \ geq T $$
= 0、それ以外の場合。
したがって、重みの値やしきい値Tを変更するだけで、さまざまな論理ゲートやブール関数を実装できます。
例
見つけましょう simplified Boolean function 次のしきい値ゲート用。

このしきい値ゲートは、三つの入力X有している1、X 2、X 3及び1つの出力をY.
入力Xに対応する重み1、X 2およびX 3であり、W 1 = 2、W 2 = 1&W 3 = -4それぞれ。
スレッショルドゲートの値はT = -1です。
ザ・ weighted sum しきい値ゲートの
$$ W = W_ {1} X_ {1} + W_ {2} X_ {2} + W_ {3} X_ {3} $$
上記の式に与えられた重みを代入します。
$$ \ Rightarrow W = 2X_ {1} + X_ {2} -4X_ {3} $$
しきい値ゲートの出力。W≥-1の場合、Yは「1」になります。それ以外の場合、Yは「0」になります。
以下 table は、入力のすべての可能な組み合わせに対する入力と出力の関係を示しています。
| 入力 | 加重和 | 出力 | ||
|---|---|---|---|---|
| $ X_ {1} $ | $ X_ {2} $ | $ X_ {3} $ | $ W = 2X_ {1} + X_ {2} -4X_ {3} $ | $ Y $ |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | -4 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | -3 | 0 |
| 1 | 0 | 0 | 2 | 1 |
| 1 | 0 | 1 | -2 | 0 |
| 1 | 1 | 0 | 3 | 1 |
| 1 | 1 | 1 | -1 | 1 |
上記の表から、次のように書くことができます。 Boolean function 出力の場合、Y as
$$ Y = \ sum m \ left(0,2,4,6,7 \ right)$$
を使用したこのブール関数の簡略化 3 variable K-Map 次の図に示します。

したがって、 simplified Boolean function 指定されたしきい値ゲートは$ Y = {X_ {3} '} + X_ {1} X_ {2} $です。
しきい値関数の合成
スレッショルドゲートは、 universal gateしきい値ゲートを使用して任意のブール関数を実装できるためです。場合によっては、単一のしきい値ゲートを使用して、いくつかの論理ゲートとブール関数を実装できないことがあります。その場合、複数のしきい値ゲートが必要になる場合があります。
これらに従ってください steps 単一のしきい値ゲートを使用してブール関数を実装するため。
Step 1 − Truth table 与えられたブール関数に対して。
Step 2 −上記の真理値表に、次の関係を示す列をもう1つ追加(インクルード)します。 weighted sums そして Threshold value。
Step 3 −以下に説明するように、入力の各組み合わせの加重和としきい値の関係を記述します。
ブール関数の出力が1の場合、加重和はこれらの入力の組み合わせのしきい値以上になります。
ブール関数の出力が0の場合、加重和はこれらの入力の組み合わせのしきい値よりも小さくなります。
Step 4 −上記の表の最後の列にあるすべての関係を満たすように、重みとしきい値の値を選択します。
step 5 −を描く symbol それらの重みとしきい値を持つしきい値ゲートの。
例
以下を実装しましょう Boolean function 単一のしきい値ゲートを使用します。
$$ Y \ left(X_ {1}、X_ {2}、X_ {3} \ right)= \ sum m \ left(0,2,4,6,7 \ right)$$
与えられたブール関数は3変数関数であり、最小項の合計形式で表されます。ザ・Truth table この機能の概要を以下に示します。
| 入力 | 出力 | ||
|---|---|---|---|
| X1 | X2 | X3 | Y |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
ここで、上記の真理値表にもう1つの列を追加(含め)しましょう。この最後の列には、weighted sums (W) and Threshold 入力の各組み合わせの値(T)。
| 入力 | 出力 | WとTの関係 | ||
|---|---|---|---|---|
| X1 | X2 | X3 | Y | |
| 0 | 0 | 0 | 1 | 0≥T |
| 0 | 0 | 1 | 0 | W 3 <T |
| 0 | 1 | 0 | 1 | W 2 ≥T |
| 0 | 1 | 1 | 0 | W 2 + W 3 <T |
| 1 | 0 | 0 | 1 | W 1 ≥T |
| 1 | 0 | 1 | 0 | W 1 + W 3 <T |
| 1 | 1 | 0 | 1 | W 1 + W 2 ≥T |
| 1 | 1 | 1 | 1 | W 1 + W 2 + W 3 ≥T |
上記の表からの結論は次のとおりです。
しきい値の値は、最初の関係に基づいてゼロまたは負のいずれかにする必要があります。
W 3の値は、第1および第2の関係に基づいて負になります。
Wの値は1及びW 2は、第5及び第三の関係に基づいて、以上のしきい値であるべきです。
W 2 Wよりも大きくなければならない3第四の関係に基づきます。
上記の結論に基づいて、重みとしきい値に次の値を選択できます。
W 1 = 2、W 2 = 1、W 3 = -4&T = -1
ザ・ symbol 上記の値のしきい値ゲートの例を以下に示します。

したがって、このしきい値ゲートは、指定されたを実装します Boolean function、$ Y \ left(X_ {1}、X_ {2}、X_ {3} \ right)= \ sum m \ left(0,2,4,6,7 \ right)$。