デジタル回路-2レベルのロジックの実現
入力と出力の間に存在するレベルの最大数は2 two level logic。つまり、論理ゲートの総数に関係なく、入力と出力の間に存在する(カスケードされる)論理ゲートの最大数は、2レベルの論理で2つです。ここで、第1レベルの論理ゲートの出力は、第2レベルの論理ゲートの入力として接続されている。
4つの論理ゲートAND、OR、NAND、NORについて考えてみます。4つの論理ゲートがあるので、2つのレベルの論理を実現する16の可能な方法が得られます。それらは、AND-AND、AND-OR、ANDNAND、AND-NOR、OR-AND、OR-OR、OR-NAND、OR-NOR、NAND-AND、NAND-OR、NANDNAND、NAND-NOR、NOR-AND、 NOR-OR、NOR-NAND、NOR-NOR。
これらの2つのレベルのロジックの実現は、次の2つのカテゴリに分類できます。
- 変性形態
- 非変性型
変性形態
単一の論理ゲートを使用して2レベルの論理実現の出力を取得できる場合、それは次のように呼ばれます。 degenerative form。明らかに、単一の論理ゲートの入力数は増加します。これにより、ロジックゲートのファンインが増加します。これは退行性の形態の利点です。
のみ 6 combinations16の組み合わせのうちの2つのレベルのロジック実現のうち、縮退形式になります。それらは、AND-AND、AND-NAND、OR-OR、OR-NOR、NAND-NOR、NORNANDです。
このセクションでは、いくつかの実現について説明します。各論理実現において、A、B、C、およびDが入力であり、Yが出力であると想定します。
AND-ANDロジック
この論理の実現では、ANDゲートは両方のレベルに存在します。下の図は、AND-AND logic 実現。

第1レベルの論理ゲートの出力を$ Y_ {1} = AB $および$ Y_ {2} = CD $として取得します。
これらの出力$ Y_ {1} $および$ Y_ {2} $は、第2レベルに存在するANDゲートの入力として適用されます。したがって、このANDゲートの出力は次のようになります。
$$ Y = Y_ {1} Y_ {2} $$
上記の式に$ Y_ {1} $と$ Y_ {2} $の値を代入します。
$$ Y = \ left(AB \ right)\ left(CD \ right)$$
$ \ Rightarrow Y = ABCD $
したがって、このAND-AND論理実現の出力は次のようになります。 ABCD。このブール関数は、4入力ANDゲートを使用して実装できます。したがって、それはdegenerative form。
AND-NANDロジック
この論理実現では、ANDゲートは第1レベルに存在し、NANDゲートは第2レベルに存在します。次の図は、AND-NAND logic 実現。
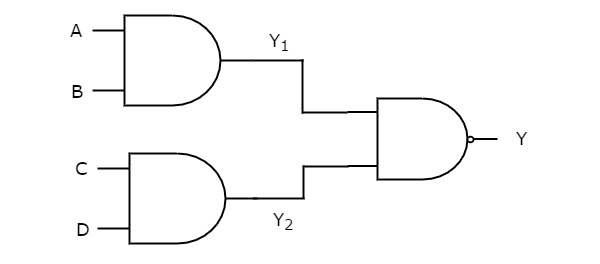
以前は、第1レベルの論理ゲートの出力を$ Y_ {1} = AB $および$ Y_ {2} = CD $として取得していました。
これらの出力$ Y_ {1} $および$ Y_ {2} $は、第2レベルに存在するNANDゲートの入力として適用されます。したがって、このNANDゲートの出力は次のようになります。
$$ Y = {\ left(Y_ {1} Y_ {2} \ right)} '$$
上記の式に$ Y_ {1} $と$ Y_ {2} $の値を代入します。
$$ Y = {\ left(\ left(AB \ right)\ left(CD \ right)\ right)} '$$
$ \ Rightarrow Y = {\ left(ABCD \ right)} '$
したがって、このAND-NAND論理実現の出力は$ {\ left(ABCD \ right)} '$です。このブール関数は、4入力NANDゲートを使用して実装できます。したがって、それはdegenerative form。
OR-ORロジック
この論理の実現では、ORゲートは両方のレベルに存在します。次の図は、OR-OR logic 実現。
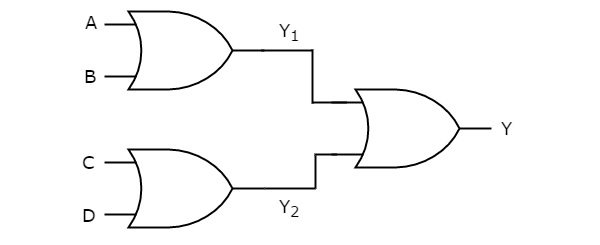
第1レベルの論理ゲートの出力を$ Y_ {1} = A + B $および$ Y_ {2} = C + D $として取得します。
これらの出力$ Y_ {1} $および$ Y_ {2} $は、第2レベルに存在するORゲートの入力として適用されます。したがって、このORゲートの出力は次のようになります。
$$ Y = Y_ {1} + Y_ {2} $$
上記の式に$ Y_ {1} $と$ Y_ {2} $の値を代入します。
$$ Y = \ left(A + B \ right)+ \ left(C + D \ right)$$
$ \ Rightarrow Y = A + B + C + D $
したがって、このOR-ORロジック実現の出力は次のようになります。 A+B+C+D。このブール関数は、4入力ORゲートを使用して実装できます。したがって、それはdegenerative form。
同様に、残りの実現がこのカテゴリに属しているかどうかを確認できます。
非変性型
単一の論理ゲートを使用して2レベルの論理実現の出力を取得できない場合、それは次のように呼び出されます。 non-degenerative form。
残り 10 combinations2つのレベルのロジックの実現のうち、非縮退形式になります。それらは、AND-OR、AND-NOR、OR-AND、OR-NAND、NAND-AND、NANDOR、NAND-NAND、NOR-AND、NOR-OR、NOR-NORです。
それでは、いくつかの実現について説明しましょう。各論理実現において、A、B、C、およびDが入力であり、Yが出力であると想定します。
AND-ORロジック
この論理実現では、ANDゲートは第1レベルに存在し、ORゲートは第2レベルに存在します。下の図は、AND-OR logic 実現。

以前は、第1レベルの論理ゲートの出力を$ Y_ {1} = AB $および$ Y_ {2} = CD $として取得していました。
これらの出力Y1とY2は、2番目のレベルに存在するORゲートの入力として適用されます。したがって、このORゲートの出力は次のようになります。
$$ Y = Y_ {1} + Y_ {2} $$
上記の式に$ Y_ {1} $と$ Y_ {2} $の値を代入します
$$ Y = AB + CD $$
したがって、このAND-OR論理実現の出力は次のようになります。 AB+CD。このブール関数はSum of Products形。単一の論理ゲートを使用して実装することはできないため、このAND-OR論理の実現はnon-degenerative form。
AND-NORロジック
この論理実現では、ANDゲートは第1レベルに存在し、NORゲートは第2レベルに存在します。次の図は、AND-NOR logic 実現。

第1レベルの論理ゲートの出力は$ Y_ {1} = AB $および$ Y_ {2} = CD $としてわかっています。
これらの出力Y1とY2は、2番目のレベルに存在するNORゲートの入力として適用されます。したがって、このNORゲートの出力は次のようになります。
$$ Y = {\ left(Y_ {1} + Y_ {2} \ right)} '$$
上記の式に$ Y_ {1} $と$ Y_ {2} $の値を代入します。
$$ Y = {\ left(AB + CD \ right)} '$$
したがって、このAND-NORロジック実現の出力は$ {\ left(AB + CD \ right)} '$です。このブール関数はAND-OR-Invert形。単一の論理ゲートを使用して実装することはできないため、このAND-NOR論理の実現はnon-degenerative form
OR-ANDロジック
この論理実現では、ORゲートは第1レベルに存在し、ANDゲートは第2レベルに存在します。次の図は、OR-AND logic 実現。

以前は、第1レベルの論理ゲートの出力を$ Y_ {1} = A + B $および$ Y_ {2} = C + D $として取得していました。
これらの出力$ Y_ {1} $および$ Y_ {2} $は、第2レベルに存在するANDゲートの入力として適用されます。したがって、このANDゲートの出力は次のようになります。
$$ Y = Y_ {1} Y_ {2} $$
上記の式に$ Y_ {1} $と$ Y_ {2} $の値を代入します。
$$ Y = \ left(A + B \ right)\ left(C + D \ right)$$
したがって、このOR-ANDロジック実現の出力は次のようになります。 (A + B) (C + D)。このブール関数はProduct of Sums形。単一の論理ゲートを使用して実装することはできないため、このOR-AND論理の実現はnon-degenerative form。
同様に、残りの実現がこのカテゴリに属しているかどうかを確認できます。