Космология - метод транзита
Транзитный метод (Kepler Space Telescope)используется, чтобы узнать размер. Падение яркости звезды на планете обычно мало чем отличается от двойной системы.
F0 поток звезды до того, как планета покрывает ее.
F1 - это поток после того, как вся планета окажется перед звездой.
Следующее изображение будет использоваться для всех расчетов.

$$ \ frac {F_0 - F_1} {F_0} = \ frac {\ pi r_p ^ {2}} {\ pi R ^ 2_ \ ast} $$
$$ \ frac {\ Delta F} {F} \ cong \ frac {r ^ 2_p} {R ^ 2_ \ ast} $$
$$ \ left (\ frac {\ Delta F} {F} \ right) _ {земля} \ cong 0.001 \% $$
$$ \ left (\ frac {\ Delta F} {F} \ right) _ {jupiter} \ cong 1 \% $$
Добиться этого с помощью наземного телескопа непросто. Это достигается телескопом Хаббл.

Здесь $ t_T $ - это время между позициями A и D, а $ t_F $ - это время между позициями B и C.
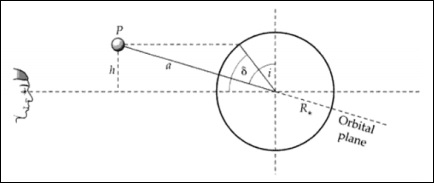
Геометрия транзита, связанная с наклоном iсистемы. Широта и наклон перехода взаимозаменяемы.
Из приведенных выше изображений мы можем написать -
$$ \ frac {h} {a} = cos (i) $$
$$ \ frac {h} {R_ \ ast} = sin (\ delta) $$
$$ cos (i) = \ frac {R_ \ ast sin (\ delta)} {a} $$
$$ y ^ 2 = (R_ \ ast + R_p) ^ 2 - h ^ 2 $$
$$ y = [(R_ \ ast + R_p) ^ 2 - h ^ 2] ^ {\ frac {1} {2}} $$
$$ sin (\ theta) = \ frac {y} {a} $$
$$ \ theta = sin ^ {- 1} \ left [\ frac {(R_ \ ast + R_p) ^ 2 - a ^ 2cos ^ 2 (i)} {a ^ 2} \ right] ^ {\ frac {1 } {2}} $$
$$ t_T = \ frac {P} {2 \ pi} \ times 2 \ theta $$
Здесь $ t_T $ - это часть периода времени, в течение которого происходит прохождение, а (2θ / 2π) - это часть угла, под которым происходит прохождение.
$$ sin (\ frac {t_T \ pi} {P}) = \ frac {R_ \ ast} {a} \ left [\ left (1+ \ frac {R_p} {R_ \ ast} \ right) ^ 2 - \ left (\ frac {a} {R_ \ ast} cos (i) \ right) ^ 2 \ right] ^ {\ frac {1} {2}} $$
Обычно a >> R ∗ >> Rp. Итак, мы можем написать -
$$ sin (\ frac {t_T \ pi} {P}) = \ frac {R_ \ ast} {a} \ left [1- \ left (\ frac {a} {R_ \ ast} cos (i) \ right ) ^ 2 \ right] ^ {\ frac {1} {2}} $$
Вот, P- продолжительность между двумя последовательными транзитами. Время прохождения намного меньше по сравнению с периодом времени на орбите. Следовательно,
$$ t_T = \ frac {P} {\ pi} \ left [\ left (\ frac {R_ \ ast} {a} \ right) ^ 2 - cos ^ 2 (i) \ right] ^ {\ frac {1 } {2}} $$
Вот, tT, P, R∗ наблюдаемые, a а также i следует выяснить.
Сейчас же,
$$ sin (\ frac {t_F \ pi} {P}) = \ frac {R_ \ ast} {a} \ left [\ left (1 - \ frac {R_p} {R_ \ ast} \ right) ^ 2 - \ left (\ frac {a} {R_ \ ast} cos \: i \ right) ^ 2 \ right] ^ {\ frac {1} {2}} $$
где $ y ^ 2 = (R_ \ ast - R_p) ^ 2 - h ^ 2 $.
Позволять,
$$ \ frac {\ Delta F} {F} = D = \ left (\ frac {R_p} {R_ \ ast} \ right) ^ 2 $$
Теперь мы можем выразить:
$$ \ frac {a} {R_ \ ast} = \ frac {2P} {\ pi} D ^ {\ frac {1} {4}} (t ^ 2_T - t ^ 2_F) ^ {- \ frac {1 } {2}} $$
Для звезд главной последовательности
$$ R_ \ ast \ propto M ^ \ alpha_ \ ast $$
$$ \ frac {R_ \ ast} {R_0} \ propto \ left (\ frac {M_ \ ast} {M_0} \ right) ^ \ alpha $$
Это дает R∗.
Следовательно, мы также получаем значение «а».
Итак, получаем «R p », «ap» и даже «i».
Для всего этого
$$ h \ leq R_ \ ast + R_p $$
$$ a \: cos \: i \ leq R_ \ ast + R_p $$
Даже для ~ 89 градусов время прохождения очень мало. Планета должна быть очень близко, чтобы получить достаточно времени для прохождения. Это дает жесткое ограничение на «i». Получив «i», мы можем вывести «m p » из измерения лучевой скорости.
Это обнаружение методом транзита называется случайным обнаружением, т. Е. Вероятностью наблюдения транзита. Расчеты вероятности перехода (вероятности наблюдения) показаны ниже.
Вероятность прохождения связана с телесным углом, определяемым двумя крайними конфигурациями прохождения, а именно:
$$ Solid \: angle \: of \: planet \: = 2 \ pi \ left (\ frac {2R_ \ ast} {a} \ right) $$
А также полный телесный угол на большой полуоси a или -
$$ Твердый \: угол \: \: сферы \: = \: 4 \ pi $$
Вероятность - это соотношение этих двух областей -
$$ = \: \ frac {площадь \: из \: неба \: покрыта \: по \: благоприятной \: ориентации} {области \: из \: неба \: покрыта \: по \: всем \: возможно \: ориентация \: of \: orbit} $$
$ = \ frac {4 \ pi a_pR_ \ ast} {4 \ pi a ^ 2_p} = \ frac {R_ \ ast} {a_p} $ $ \ frac {area \: of \: hollow \: cyclinder} {area \ : of \: сфера} $
Эта вероятность не зависит от наблюдателя.
Что следует помнить
- Для определения размера используется метод транзита (космический телескоп Кеплера).
- Обнаружение транзитным методом - это случайное обнаружение.
- Планета должна быть очень близко, чтобы иметь достаточно времени для прохождения.
- Вероятность прохождения связана с телесным углом планеты.
- Эта вероятность не зависит от системы координат наблюдателя.