การบัญชีต้นทุน - การวิเคราะห์ CVP

การวิเคราะห์ต้นทุน - ปริมาณ - กำไร (CVP) เรียกอีกอย่างว่าการวิเคราะห์แบบแบ่งจุด องค์กรธุรกิจทุกแห่งทำงานเพื่อเพิ่มผลกำไรสูงสุด ด้วยความช่วยเหลือของการวิเคราะห์ CVP ผู้บริหารจะศึกษาความสัมพันธ์ระหว่างผลกำไรและระดับการผลิต

การวิเคราะห์ CVP เกี่ยวข้องกับระดับของกิจกรรมที่ยอดขายรวมเท่ากับต้นทุนรวมและเรียกว่าจุดคุ้มทุน กล่าวอีกนัยหนึ่งเราศึกษามูลค่าการขายต้นทุนและกำไรในระดับการผลิตต่างๆ การวิเคราะห์ CVP เน้นความสัมพันธ์ระหว่างต้นทุนมูลค่าการขายและผลกำไร

สมมติฐาน

ให้เราผ่านสมมติฐานสำหรับการวิเคราะห์ CVP:

• ต้นทุนผันแปรยังคงผันแปรและต้นทุนคงที่ยังคงที่ในทุกระดับการผลิต

• ปริมาณการขายไม่มีผลต่อราคาขายของผลิตภัณฑ์ เราสามารถถือว่าราคาขายคงที่

• ในทุกระดับการขายปริมาณวัสดุและต้นทุนแรงงานจะคงที่

• ประสิทธิภาพและประสิทธิผลยังคงไม่เปลี่ยนแปลงในทุกระดับของปริมาณการขาย

• การผสมผสานการขายในทุกระดับการขายยังคงคงที่ในสถานการณ์ที่มีหลายผลิตภัณฑ์

• ปัจจัยที่เกี่ยวข้องซึ่งมีผลต่อต้นทุนและรายได้คือปริมาณเท่านั้น

• ปริมาณการขายเท่ากับปริมาณการผลิต

สมการต้นทุนส่วนเพิ่ม

สมการสำหรับองค์ประกอบของต้นทุนมีดังนี้:

Sales = Variable costs + Fixed Expenses ± Profit /Loss

                     Or
                     
Sales – Variable Cost = Fixed Expenses ± Profit /Loss

                     Or
                     
Sales – Variable Cost = Contribution

จำเป็นต้องเข้าใจแนวคิดสี่ประการต่อไปนี้การคำนวณและการประยุกต์ใช้เพื่อทราบความสัมพันธ์ทางคณิตศาสตร์ระหว่างต้นทุนปริมาณและกำไร:

• Contribution
• อัตราส่วนปริมาณกำไร (P / V Ratio หรือเงินสมทบ / ยอดขาย (C / S))
• จุดคุ้มทุน
• ขอบด้านความปลอดภัย

เงินสมทบ

Contribution = Sales – Marginal Cost

เราได้กล่าวถึงการมีส่วนร่วมในหัวข้อต้นทุนส่วนเพิ่มข้างต้นแล้ว

อัตราส่วนกำไรต่อปริมาณ

อัตราส่วนกำไร / ปริมาณ (P / V) คำนวณในขณะที่ศึกษาความสามารถในการทำกำไรของการดำเนินงานของธุรกิจและเพื่อสร้างความสัมพันธ์ระหว่างการขายและการมีส่วนร่วม เป็นหนึ่งในอัตราส่วนที่สำคัญที่สุดซึ่งคำนวณได้จาก:

อัตราส่วน P / V มีความสัมพันธ์โดยตรงกับผลกำไร อัตราส่วน P / V ที่สูงขึ้นกำไรมากขึ้นและในทางกลับกัน

จุดคุ้มทุน

เมื่อต้นทุนรวมในการดำเนินธุรกิจเท่ากับยอดขายทั้งหมดจะเรียกว่าจุดคุ้มทุน เงินสมทบเท่ากับต้นทุนคงที่ ณ จุดนี้ สูตรคำนวณจุดคุ้มทุนมีดังนี้

จุดคุ้มทุนตามยอดขายทั้งหมด:

การคำนวณผลผลิตหรือมูลค่าการขายที่ได้รับผลกำไรที่ต้องการ:

จุดคุ้มทุนคอมโพสิต

บริษัท อาจมีหน่วยการผลิตที่แตกต่างกันโดยที่พวกเขาอาจผลิตผลิตภัณฑ์เดียวกัน ในกรณีนี้ต้นทุนคงที่รวมของแต่ละหน่วยการผลิตและยอดขายรวมทั้งหมดจะถูกนำมาพิจารณาเพื่อหา BEP

• Constant Product - วิธีการผสมในแนวทางนี้อัตราส่วนจะคงที่สำหรับผลิตภัณฑ์ของหน่วยการผลิตทั้งหมด

• Variable Product - วิธีผสมในแนวทางนี้ความชอบของผลิตภัณฑ์ขึ้นอยู่กับอัตราส่วนที่ใหญ่กว่า

ขอบด้านความปลอดภัย

การขายส่วนเกินที่ BEP เรียกว่าขอบความปลอดภัย ดังนั้น,

Margin of safety = Actual Sales − Sales at BEP

อัตราความปลอดภัยอาจคำนวณได้โดยใช้สูตรต่อไปนี้:

แผนภูมิจุดคุ้มทุน

แผนภูมิจุดคุ้มทุนเป็นการนำเสนอแบบกราฟิกที่มีประโยชน์ที่สุดของการคิดต้นทุนส่วนเพิ่ม จะแปลงข้อมูลทางบัญชีเป็นรายงานที่อ่านได้ที่มีประโยชน์ ผลกำไรขาดทุนและต้นทุนโดยประมาณสามารถกำหนดได้ในระดับการผลิตที่แตกต่างกัน ให้เราเป็นตัวอย่าง

ตัวอย่าง

คำนวณจุดคุ้มทุนและวาดแผนภูมิจุดคุ้มทุนจากข้อมูลต่อไปนี้:

Fixed Cost    = Rs 2,50,000
Variable Cost = Rs 15 per unit
Selling Price = Rs 25 per unit
Production level in units 12,000, 15,000, 20,000, 25,000, 30,000, and 40,000.

Solution:

ที่ระดับการผลิต 25,000 หน่วยต้นทุนทั้งหมดจะอยู่ที่ 6,25,000 รูปี

(คำนวณเป็น (25000 × 14) + 2,50000)

คำแถลงที่แสดงกำไรและส่วนต่างของความปลอดภัยในระดับการผลิตที่แตกต่างกันการขายจุดคุ้มทุน = 6,25,000 รูปี (25,000 x 25)
การผลิต (ในหน่วย)	ยอดขายรวม (ใน Rs)	ค่าใช้จ่ายทั้งหมด (ใน Rs)	กำไร (ขาย - ต้นทุน) (ใน Rs)	ขอบด้านความปลอดภัย (กำไร / เงินสมทบต่อหน่วย) (ในหน่วย)
12000	3,00,000	4,30,000	-1,30,000
15000	3,75,000	4,75,000	-1,00,000
20000	5,00,000	5,50,000	-50,000
25000	6,25,000	6,25,000	(BEP)	(BEP)
30000	7,50,000	7,00,000	50,000	5,000
40000	10,00,000	8,50,000	1,50,000	15,000

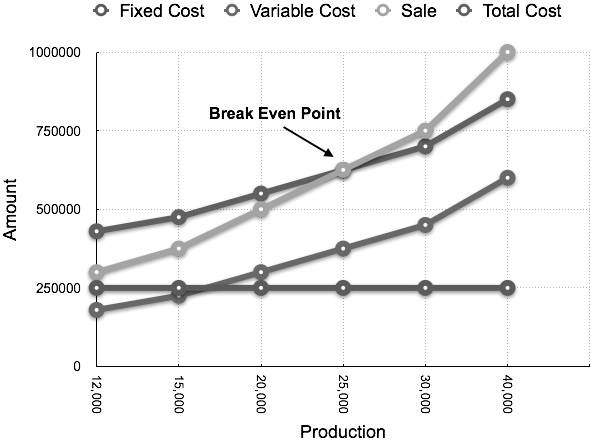
แผนภูมิที่สอดคล้องกันที่ลงจุดเป็นการผลิตเทียบกับจำนวนเงินจะปรากฏดังนี้: