Kozmoloji - Açısal Çap Mesafesi
Bu bölümde, Açısal Çap Mesafesinin ne olduğunu ve Kozmolojiye nasıl yardımcı olduğunu anlayacağız.
Mevcut evren için -
$ \ Omega_ {m, 0} \: = \: 0,3 $
$ \ Omega _ {\ kama, 0} \: = \: 0.69 $
$ \ Omega_ {rad, 0} \: = \: 0.01 $
$ \ Omega_ {k, 0} \: = \: 0 $
Şimdiye kadar iki tür mesafeyi inceledik -
Proper distance (lp) - Fotonların kaynaktan bize geldiği mesafe, yani Instantaneous distance.
Comoving distance (lc) - Genişlemeyen bir boşluktaki nesneler arasındaki mesafe, yani distance in a comoving frame of reference.
Redshift'in Fonksiyonu Olarak Mesafe
Zamanda bir foton yayan bir galaksi düşünün t1 gözlemci tarafından tespit edilen t0. Galaksiye olan uygun mesafeyi şu şekilde yazabiliriz:
$$ l_p = \ int_ {t_1} ^ {t_0} cdt $$
Galaksinin kırmızıya kaymasına izin ver z,
$$ \ Rightarrow \ frac {\ mathrm {d} z} {\ mathrm {d} t} = - \ frac {1} {a ^ 2} \ frac {\ mathrm {d} a} {\ mathrm {d} t} $$
$$ \ Rightarrow \ frac {\ mathrm {d} z} {\ mathrm {d} t} = - \ frac {\ frac {\ mathrm {d} a} {\ mathrm {d} t}} {a} \ frac {1} {a} $$
$$ \ bu nedenle \ frac {\ mathrm {d} z} {\ mathrm {d} t} = - \ frac {H (z)} {a} $$
Şimdi, galaksinin her an uzaklaşması t olacak -
$$ l_c = \ frac {l_p} {a (t)} $$
$$ l_c = \ int_ {t_1} ^ {t_0} \ frac {cdt} {a (t)} $$
Z açısından,
$$ l_c = \ int_ {t_0} ^ {t_1} \ frac {cdz} {H (z)} $$
Mesafeleri bulmanın iki yolu vardır, bunlar aşağıdaki gibidir:
Akı-Parlaklık İlişkisi
$$ F = \ frac {L} {4 \ pi d ^ 2} $$
nerede d kaynaktaki mesafedir.
Bir Kaynağın Açısal Çap Mesafesi
Bir kaynağın boyutunu bilirsek, açısal genişliği bize onun gözlemciden uzaklığını söyleyecektir.
$$ \ theta = \ frac {D} {l} $$
nerede l kaynağın açısal çap mesafesidir.
θ kaynağın açısal boyutudur.
D kaynağın boyutudur.
D boyutunda ve açısal boyutta bir galaksi düşünün dθ.
Biz biliyoruz ki,
$$ d \ theta = \ frac {D} {d_A} $$
$$ \ bu nedenle D ^ 2 = a (t) ^ 2 (r ^ 2 d \ theta ^ 2) \ quad \ çünkü dr ^ 2 = 0; \: d \ phi ^ 2 \ yaklaşık 0 $$
$$ \ Rightarrow D = a (t) rd \ theta $$
Değiştirme r -e rc, galaksinin yaklaşan mesafesi, bizde -
$$ d \ theta = \ frac {D} {r_ca (t)} $$
Burada, eğer seçersek t = t0, galaksiye şimdiki mesafeyi ölçüyoruz. FakatDfotonun emisyonu anında ölçülür. Bu nedenle kullanarakt = t0galaksiye daha büyük bir mesafe ve dolayısıyla boyutu küçümsüyoruz. Bu nedenle zamanı kullanmalıyızt1.
$$ \ bu nedenle d \ theta = \ frac {D} {r_ca (t_1)} $$
Bunu önceki sonuçla karşılaştırdığımızda, şunu elde ederiz -
$$ d_ \ wedge = a (t_1) r_c $$
$$ r_c = l_c = \ frac {d_ \ wedge} {a (t_1)} = d_ \ wedge (1 + z_1) \ quad \ çünkü 1 + z_1 = \ frac {1} {a (t_1)} $$
Bu nedenle,
$$ d_ \ wedge = \ frac {c} {1 + z_1} \ int_ {0} ^ {z_1} \ frac {dz} {H (z)} $$
dA nesnenin Açısal Çap Mesafesidir.
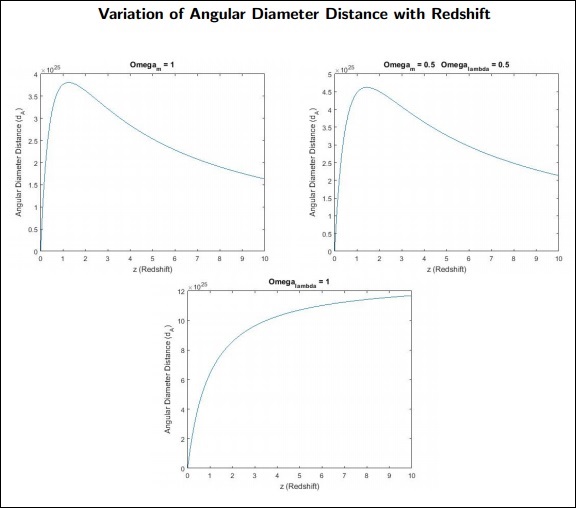
Hatırlanacak noktalar
Bir kaynağın boyutunu bilirsek, açısal genişliği bize onun gözlemciden uzaklığını söyleyecektir.
Uygun mesafe, fotonların kaynaktan bize kadar gittiği mesafedir.
Geliş mesafesi, genişlemeyen bir uzayda nesneler arasındaki mesafedir.