Kozmoloji - Transit Yöntemi
Transit Yöntemi (Kepler Space Telescope)boyutu bulmak için kullanılır. Bir yıldızın parlaklığındaki bir gezegenin düşüşü, genellikle bir ikili sistemden çok daha azdır.
F0 gezegen onu örtmeden önce yıldızın akışıdır.
F1 tüm gezegen yıldızın önünde olduktan sonraki akıdır.
Tüm hesaplamalar için aşağıdaki resim kullanılacaktır.

$$ \ frac {F_0 - F_1} {F_0} = \ frac {\ pi r_p ^ {2}} {\ pi R ^ 2_ \ ast} $$
$$ \ frac {\ Delta F} {F} \ cong \ frac {r ^ 2_p} {R ^ 2_ \ ast} $$
$$ \ left (\ frac {\ Delta F} {F} \ right) _ {dünya} \ cong 0.001 \% $$
$$ \ left (\ frac {\ Delta F} {F} \ right) _ {jupiter} \ cong 1 \% $$
Yer tabanlı teleskopla bunu başarmak kolay değildir. Hubble teleskopu ile elde edilir.

Burada, $ t_T $, A ve D konumları arasındaki zamandır ve $ t_F $, B ve C konumları arasındaki zamandır.
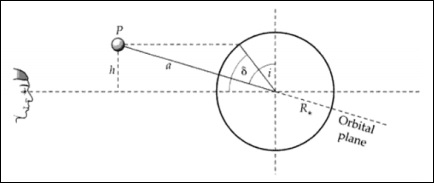
Eğimle ilgili bir geçişin geometrisi isistemin. Geçiş enlemi ve eğimi birbirinin yerine kullanılabilir.
Yukarıdaki resimlerden yazabiliriz -
$$ \ frac {h} {a} = cos (i) $$
$$ \ frac {h} {R_ \ ast} = sin (\ delta) $$
$$ cos (i) = \ frac {R_ \ ast sin (\ delta)} {a} $$
$$ y ^ 2 = (R_ \ ast + R_p) ^ 2 - h ^ 2 $$
$$ y = [(R_ \ ast + R_p) ^ 2 - h ^ 2] ^ {\ frac {1} {2}} $$
$$ sin (\ theta) = \ frac {y} {a} $$
$$ \ theta = sin ^ {- 1} \ left [\ frac {(R_ \ ast + R_p) ^ 2 - a ^ 2cos ^ 2 (i)} {a ^ 2} \ right] ^ {\ frac {1 } {2}} $$
$$ t_T = \ frac {P} {2 \ pi} \ times 2 \ theta $$
Burada, $ t_T $, geçişin gerçekleştiği bir zaman diliminin kesri ve (2θ / 2π), geçişin gerçekleştiği açının kesri.
$$ sin (\ frac {t_T \ pi} {P}) = \ frac {R_ \ ast} {a} \ left [\ left (1+ \ frac {R_p} {R_ \ ast} \ sağ) ^ 2 - \ left (\ frac {a} {R_ \ ast} cos (i) \ right) ^ 2 \ right] ^ {\ frac {1} {2}} $$
Genellikle, bir >> R ∗ >> Rp. Yani yazabiliriz -
$$ sin (\ frac {t_T \ pi} {P}) = \ frac {R_ \ ast} {a} \ left [1- \ left (\ frac {a} {R_ \ ast} cos (i) \ right ) ^ 2 \ sağ] ^ {\ frac {1} {2}} $$
Buraya, Pardışık iki geçiş arasındaki süredir. Geçiş süresi yörünge zaman dönemine göre çok daha azdır. Bu nedenle
$$ t_T = \ frac {P} {\ pi} \ left [\ left (\ frac {R_ \ ast} {a} \ right) ^ 2 - cos ^ 2 (i) \ sağ] ^ {\ frac {1 } {2}} $$
Buraya, tT, P, R∗ gözlemlenebilirler a ve i bulunmalı.
Şimdi,
$$ sin (\ frac {t_F \ pi} {P}) = \ frac {R_ \ ast} {a} \ left [\ left (1 - \ frac {R_p} {R_ \ ast} \ sağ) ^ 2 - \ left (\ frac {a} {R_ \ ast} cos \: i \ right) ^ 2 \ right] ^ {\ frac {1} {2}} $$
burada, $ y ^ 2 = (R_ \ ast - R_p) ^ 2 - h ^ 2 $.
İzin Vermek,
$$ \ frac {\ Delta F} {F} = D = \ left (\ frac {R_p} {R_ \ ast} \ sağ) ^ 2 $$
Şimdi ifade edebiliriz,
$$ \ frac {a} {R_ \ ast} = \ frac {2P} {\ pi} D ^ {\ frac {1} {4}} (t ^ 2_T - t ^ 2_F) ^ {- \ frac {1 } {2}} $$
Ana sekans yıldızları için,
$$ R_ \ ast \ propto M ^ \ alpha_ \ ast $$
$$ \ frac {R_ \ ast} {R_0} \ propto \ left (\ frac {M_ \ ast} {M_0} \ right) ^ \ alpha $$
Bu verir R∗.
Dolayısıyla, 'a' değerini de alıyoruz.
Böylece 'R p ', 'p' ve hatta 'i' elde ederiz .
Bütün bunlar için
$$ h \ leq R_ \ ast + R_p $$
$$ a \: cos \: i \ leq R_ \ ast + R_p $$
Hatta ~ 89 derece için geçiş süresi çok azdır. Yeterli bir geçiş süresi elde etmek için gezegenin çok yakın olması gerekir. Bu, 'i' üzerinde sıkı bir kısıtlama sağlar. 'İ' yi elde ettiğimizde , radyal hız ölçümünden 'm p ' elde edebiliriz .
Geçiş yöntemiyle yapılan bu tespit, şans tespiti, yani bir transit gözlemleme olasılığı olarak adlandırılır. Transit olasılık (gözlemleme olasılığı) hesaplamaları aşağıda gösterilmiştir.
Geçiş olasılığı, iki aşırı geçiş konfigürasyonunun izlediği katı açı ile ilgilidir, yani -
$$ Katı \: açı \: / \: gezegen \: = 2 \ pi \ left (\ frac {2R_ \ ast} {a} \ right) $$
Yarı büyük bir eksendeki toplam katı açının yanı sıra a veya -
$$ Katı \: açı \: / \: küre \: = \: 4 \ pi $$
Olasılık, bu iki alanın oranıdır -
$$ = \: \ frac {alan \: arasında \: gökyüzü \: örtülü \: tarafından \: uygun \: yön} {alan \: \: gökyüzü \: örtülü \: tarafından \: tümü \: mümkün \: yön \: / \: orbit} $$
$ = \ frac {4 \ pi a_pR_ \ ast} {4 \ pi a ^ 2_p} = \ frac {R_ \ ast} {a_p} $ $ \ frac {alan \: / \: içi boş \: döngü} {alan \ : / \: küre} $
Bu olasılık gözlemciden bağımsızdır.
Hatırlanacak noktalar
- Transit Yöntemi (Kepler Uzay Teleskobu) boyutu bulmak için kullanılır.
- Transit Yöntemi ile Tespit, bir tesadüf tespitidir.
- Yeterli geçiş süresi elde etmek için gezegen çok yakın olmalıdır.
- Geçiş olasılığı, gezegenin katı açısıyla ilgilidir.
- Bu olasılık, gözlemcinin referans çerçevesinden bağımsızdır.