Kozmoloji - Radyasyona Hakim Olan Evren
Bu bölümde, Radyasyona Hakim Olan Evren ile ilgili Friedmann Denklemlerinin Çözümlerini tartışacağız. Başlangıçta, maddenin enerji yoğunluğunu radyasyonunkiyle karşılaştırıyoruz. Bu, evrenimizin maddeye mi yoksa radyasyona mı hakim olduğunu görmemizi sağlayacaktır.
Radyasyonun Enerji Yoğunluğu
Mevcut evrende yaygın olan radyasyon yıldız kaynaklarına çok az atfedilebilir, ancak esas olarak kalan CMB'den (Kozmik Mikrodalga Arka Planı) kaynaklanmaktadır.
Radyasyonun enerji yoğunluğu, $ \ epsilon _ {\ gamma, 0} $, aşağıdaki gibi ifade edilebilir -
$$ \ epsilon _ {\ gamma, 0} = aT_0 ^ 4 $$
Buraya, a $ (8 \ pi ^ 5k_B ^ 4) / (15h ^ 3c ^ 2) $ ifadesine eşit olan radyasyon sabitidir a = 7.5657 × 10−15erg\: cm−3 K−4. Burada ele aldığımız Sıcaklık, T0, CMB'ye karşılık gelen siyah cisminkine karşılık gelir.
Sonuçları değiştirerek, elimizde,
$$ \ epsilon _ {\ gamma, 0} = aT_0 ^ 4 = 4 \ times 10 ^ {- 13} erg \: cm ^ {- 3} $$
Maddenin Enerji Yoğunluğu
Aşağıdaki hesaplamalarda, düz bir evren ve K = 0 ile çalışma varsayımına sahibiz. Maddenin enerji yoğunluğunu $ \ epsilon = \ rho c ^ 2 $ olarak kabul ediyoruz. Aşağıdakileri dikkate alıyoruz -
$$ \ rho_ {m, 0} c ^ 2 = 0.3 \ rho_ {c, 0} c ^ 2 = 0.3 \ times \ frac {3H_0 ^ 2} {8 \ pi G} \ times c ^ 2 $$
$$ \ rho_ {m, 0} c ^ 2 \ simeq 2 \ times 10 ^ {- 8} erg \: cm ^ {- 3} $$
$$ \ rho_ {b, 0} c ^ 2 = 0.03 \ rho_ {c, 0} c ^ 2 = 0.03 \ times \ frac {3H_0 ^ 2} {8 \ pi G} \ times c ^ 2 $$
$$ \ rho_ {b, 0} c ^ 2 \ simeq 2 \ times 10 ^ {- 9} erg \: cm ^ {- 3} $$
Böylece, yukarıdaki hesaplamadan, maddenin egemen olduğu bir evrende yaşadığımızı görüyoruz. Bu, SPK'nın çok soğuk olmasıyla desteklenebilir. Geriye dönüp baktığımızda, CMB sıcaklığının yükselmesini sağlayacağız ve evrene radyasyonun hakim olduğu bir çağın olabileceği sonucuna varabileceğiz.
Yoğunluk Değişimi ve Ölçek Faktörü
Sıvı denklemi bize şunu gösteriyor -
$$ \ dot {\ rho} + 3 \ frac {\ dot {a}} {a} \ left (\ rho + \ frac {P} {c ^ 2} \ right) = 0 $$
Tozlu bir evren düşünürsek, P = 0 olur. Önceki sonuçları bir kenara bırakırsak, evrene radyasyonun hakim olduğunu düşünürüz.
$$ \ dot {\ rho} _ {rad} + 3 \ frac {\ dot {a}} {a} \ left (\ rho_ {rad} + \ frac {P} {c ^ 2} \ right) = 0 $$
$ P_ {rad} = \ rho c ^ {2/3} $ 'ın basınç ilişkisini kullanarak -
$$ \ dot {\ rho} _ {rad} + 3 \ frac {\ dot {a}} {a} \ left (\ rho_ {rad} + \ frac {\ rho_ {rad}} {3} \ right) = 0 $$
$$ \ dot {\ rho} _ {rad} + 4 \ frac {\ dot {a}} {a} (\ rho_ {rad}) = 0 $$
Daha fazla basitleştirme konusunda,
$$ \ frac {1} {a ^ 4} \ frac {\ mathrm {d}} {\ mathrm {d} t} (\ rho_ {rad} a ^ 4) = 0 $$
$$ \ rho_ {rad} a ^ 4 = \: Constant $$
$$ \ rho_ {rad} \ propto \ frac {1} {a ^ 4} $$
Yukarıdaki sonuç gösterileri ters 4 th $ \ rho $ ile güç varyasyonu.
Bu, fiziksel olarak, artan hacimdeki değişimden gelen $ a ^ {- 3} $ olarak yorumlanabilir. Kalan $ a ^ {- 1} $, evrendeki uzayın genişlemesi nedeniyle foton tarafından kaybedilen enerji olarak değerlendirilebilir (Kozmolojik kırmızıya kayma 1 + z = a -1 ).
Aşağıdaki görüntü, zamanla madde ve radyasyon yoğunluğunun değişimini göstermektedir.
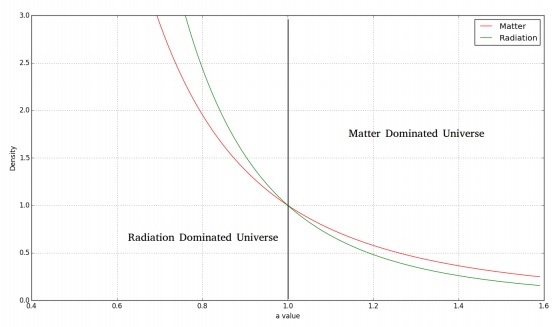
Düz, radyasyonun hakim olduğu bir evren için, Friedmann denklemini aşağıdaki gibi elde ederiz:
$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G \ rho} {3} $$
$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ frac {\ rho_0} {a ^ 4} $$
Basitleştirme ve çözümü diferansiyel denkleme uygulama konusunda elimizde -
$$ (\ nokta {a}) ^ 2 = \ frac {8 \ pi G \ rho_0} {3a ^ 2} $$
$$ \ Rightarrow a (t) \ propto t ^ {\ frac {1} {2}} $$
Böylece, elimizde -
$$ a (t) = a_0 \ left (\ frac {t} {t_0} \ right) ^ {\ frac {1} {2}} $$
Yukarıdaki denklemden, ölçek faktörünün artış hızının tozlu evreninkinden daha küçük olduğunu görüyoruz.
Hatırlanacak noktalar
Mevcut evrende yaygın olan radyasyon yıldız kaynaklarına çok az atfedilebilir.
Tozlu bir evren için basınç sıfırdır.
SPK çok soğuk.