Excel Veri Finansal Analizi
Excel ile finansal analizi kolay bir şekilde gerçekleştirebilirsiniz. Excel size PMT, PV, NPV, XNPV, IRR, MIRR, XIRR ve benzeri gibi finansal analiz sonuçlarına hızlı bir şekilde ulaşmanızı sağlayan çeşitli finansal işlevler sağlar.
Bu bölümde, analiziniz için bu işlevleri nerede ve nasıl kullanabileceğinizi öğreneceksiniz.
Annuity nedir?
Yıllık gelir, sürekli bir süre boyunca yapılan bir dizi sürekli nakit ödemedir. Örneğin, emeklilik, sigorta ödemeleri, ev kredisi, ipotek vb. İçin tasarruflar. Yıllık ödeme fonksiyonlarında -
- Pozitif bir sayı alınan parayı temsil eder.
- Negatif bir sayı, ödenen nakiti temsil eder.
Bir dizi Gelecek Ödemenin Mevcut Değeri
Bugünkü değer, gelecekteki bir dizi ödemenin şu anda değerinde olduğu toplam tutardır. Excel işlevlerini kullanarak bugünkü değeri hesaplayabilirsiniz -
PV- Bir faiz oranını ve bir dizi gelecekteki ödemeleri (negatif değerler) ve geliri (pozitif değerler) kullanarak bir yatırımın bugünkü değerini hesaplar. Nakit akışlarından en az biri pozitif ve en az biri negatif olmalıdır.
NPV - Bir yatırımın net bugünkü değerini, bir iskonto oranı ve bir dizi dönemsel gelecek ödemeler (negatif değerler) ve gelir (pozitif değerler) kullanarak hesaplar.
XNPV - Dönemsel olması gerekmeyen bir nakit akışları çizelgesi için net bugünkü değeri hesaplar.
Note that -
PV nakit akışları sabit olmalıdır, oysa NPV nakit akışları değişken olabilir.
PV nakit akışları dönemin başında veya sonunda olabilirken, NPV nakit akışları dönemin sonunda olmalıdır.
NBD nakit akışları periyodik olmalıdır, oysa XNPV nakit akışlarının periyodik olması gerekmez.
Bu bölümde, PV ile nasıl çalışılacağını anlayacaksınız. Daha sonraki bir bölümde NPV hakkında bilgi edineceksiniz.
Misal
Bir buzdolabı satın aldığınızı varsayalım. Satış görevlisi size buzdolabının fiyatının 32000 olduğunu, ancak tutarı 8 yılda yıllık% 13 faiz oranı ve 6000 yıllık ödeme seçeneğiniz olduğunu söyler. Ayrıca ödeme yapma seçeneğiniz de vardır. her yılın başında veya sonunda.
Bu seçeneklerden hangisinin sizin için yararlı olduğunu bilmek istiyorsunuz.
Excel işlevi PV'yi kullanabilirsiniz -
PV (rate, nper, pmt, [fv ], [type])Her yılın sonunda ödemelerle bugünkü değeri hesaplamak için, türü atlayın veya tür için 0 belirtin.
Her yılın sonunda yapılan ödemelerle bugünkü değeri hesaplamak için, tür olarak 1 belirtin.

Aşağıdaki sonuçları alacaksınız -

Bu nedenle,
- Ödemeyi şimdi yaparsanız, 32.000 şimdiki değeri ödemeniz gerekir.
- Yıl sonunda ödemeli yıllık ödemeleri seçerseniz, bugünkü değerin 28.793'ünü ödemeniz gerekir.
- Yıl sonunda ödemeli yıllık ödemeleri seçerseniz, bugünkü değerin 32.536'sını ödemeniz gerekir.
2. seçeneğin sizin için faydalı olduğunu açıkça görebilirsiniz.
EMI nedir?
Bir Eşit Aylık Taksit (EMI), Investopedia tarafından "Bir borçlu tarafından bir borç verene her takvim ayında belirli bir tarihte yapılan sabit bir ödeme tutarı olarak tanımlanır. Eşit aylık taksitler, her ay hem faiz hem de anaparayı ödemek için kullanılır. yıl belirli bir sayıda, kredi tam olarak ödenir. "
Kredide EMI
Excel'de, bir kredinin EMI'sini PMT işlevi ile hesaplayabilirsiniz.
Diyelim ki yıllık% 11,5 faiz oranı ve kredinin vadesi 25 yıl olan 5000000'lük bir ev kredisi almak istiyorsunuz. EMI'nizi aşağıdaki şekilde bulabilirsiniz -
- Aylık faiz oranını hesaplayın (Yıllık Faiz Oranı / 12)
- Aylık ödeme sayısını hesaplayın (yıl sayısı * 12)
- EMI'yi hesaplamak için PMT işlevini kullanın

Gözlemlediğiniz gibi
- Mevcut Değer (PV), kredi miktarıdır.
- Vade sonunda kredi tutarının 0 olması gerektiği için Gelecek Değeri (GD) 0'dır.
- EMI'ler her ayın başında ödendiği için tür 1'dir.
Aşağıdaki sonuçları alacaksınız -

Bir Kredinin Aylık Anapara ve Faiz Ödemesi
EMI, hem faiz hem de anaparanın bir kısmı ödemesini içerir. Zaman arttıkça, EMI'nin bu iki bileşeni değişecek ve dengeyi azaltacaktır.
Almak
Aylık ödemelerinizin faiz kısmını Excel IPMT işlevini kullanabilirsiniz.
Aylık ödemelerinizin ana kısmının ödenmesi, Excel PPMT işlevini kullanabilirsiniz.
Örneğin, 8 aylık bir vade için yıllık% 16 oranında 1.000.000 kredi aldıysanız. 8 ay boyunca EMI, azalan faiz tutarları, artan anapara ödemeleri ve azalan kredi bakiyesi için değerler alabilirsiniz. 8 ayın sonunda kredi bakiyesi 0 olacaktır.
Aşağıda verilen prosedürü izleyin.
Step 1 - EMI'yi aşağıdaki gibi hesaplayın.

Bu, Rs EMI'si ile sonuçlanır. 13261.59.

Step 2 - Daha sonra, aşağıda gösterildiği gibi 8 aylık EMI'nin faiz ve ana kısımlarını hesaplayın.

Aşağıdaki sonuçları alacaksınız.

Faiz ve Anapara iki Dönem arasında ödenir
İki dönem arasında ödenen faiz ve anaparayı hesaplayabilirsiniz.
CUMIPMT işlevini kullanarak 2. ve 3. aylar arasında ödenen kümülatif faizi hesaplayın .
2. ve 3. ayların faiz değerlerini toplayan sonucu doğrulayın .
CUMPRINC işlevini kullanarak 2. ve 3. aylar arasında ödenen kümülatif anaparayı hesaplayın .
2. ve 3. aylar için temel değerleri özetleyen sonucu doğrulayın .

Aşağıdaki sonuçları alacaksınız.

Hesaplamalarınızın doğrulama sonuçlarınızla eşleştiğini görebilirsiniz.
Faiz Oranının Hesaplanması
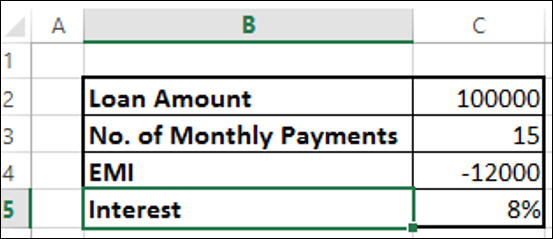
100.000 kredi aldığınızı ve aylık maksimum 12000 TL ödeyerek 15 ayda geri ödemek istediğinizi varsayalım. Ödemek zorunda olduğunuz faiz oranını bilmek isteyebilirsiniz.
Excel RATE işleviyle faiz oranını bulun -

Sonucu% 8 olarak alacaksınız.
Kredi Vadesinin Hesaplanması
% 10 faiz oranıyla 100.000 kredi aldığınızı varsayalım. Aylık maksimum 15.000 ödeme istiyorsunuz. Krediyi temizlemenizin ne kadar süreceğini bilmek isteyebilirsiniz.
Excel NPER işlevi ile ödeme sayısını bulun

Sonucu 12 ay olarak alacaksınız.

Yatırım Kararları
Bir yatırım yapmak istediğinizde, farklı seçenekleri karşılaştırır ve daha iyi getiri sağlayacak olanı seçersiniz. Net bugünkü değer, belirli bir süre boyunca nakit akışlarını karşılaştırmak ve hangisinin daha iyi olduğuna karar vermek için kullanışlıdır. Nakit akışları düzenli, periyodik aralıklarla veya düzensiz aralıklarla gerçekleşebilir.
İlk olarak, durumu ele alıyoruz regular, periodical cash flows.
Şu andan itibaren n yıl içinde farklı noktalarda alınan bir nakit akışı dizisinin bugünkü net değeri (n, bir kesir olabilir) 1/(1 + r)n, burada r yıllık faiz oranıdır.
Aşağıdaki iki yatırımı 3 yıllık bir dönemde düşünün.
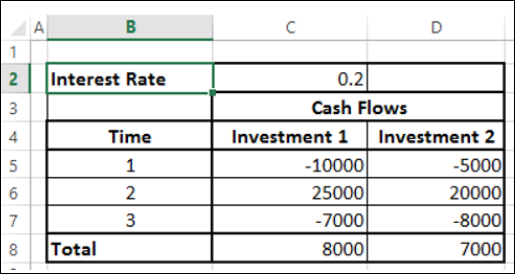
Görünen değerde Yatırım 1, Yatırım 2'den daha iyi görünüyor. Ancak, hangi yatırımın daha iyi olduğuna ancak bugün itibariyle yatırımın gerçek değerini bildiğinizde karar verebilirsiniz. Getirileri hesaplamak için NPV işlevini kullanabilirsiniz.
Nakit akışları gerçekleşebilir
- Her yılın sonunda.
- Her yılın başında.
- Her yılın ortasında.
NPV fonksiyonu, nakit akışlarının yıl sonunda olduğunu varsayar. Nakit akışları farklı zamanlarda meydana gelirse, NPV ile hesaplamayla birlikte bu belirli faktörü de hesaba katmanız gerekir.
Nakit akışlarının yıl sonunda gerçekleştiğini varsayalım. O zaman hemen NPV işlevini kullanabilirsiniz.
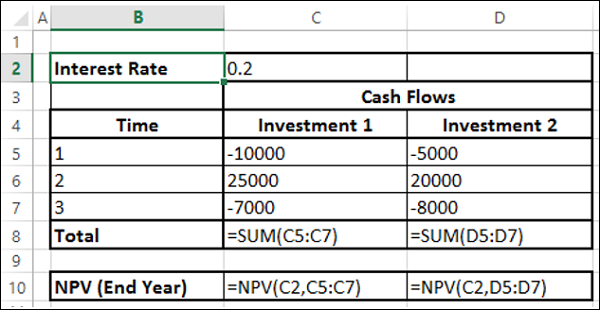
Aşağıdaki sonuçları alacaksınız -

Yatırım 2 için NBD'nin Yatırım 1'den daha yüksek olduğunu gözlemlediğiniz gibi, Yatırım 2 daha iyi bir seçimdir. Bu sonucu, Yatırım 2'nin nakit çıkışları, Yatırım 1'inkine kıyasla daha sonraki dönemlerde olduğu için aldınız.
Yılın Başındaki Nakit Akışları
Nakit akışlarının her yılın başında gerçekleştiğini varsayalım. Böyle bir durumda, halihazırda cari değeri temsil ettiği için ilk nakit akışını NPV hesaplamasına dahil etmemelisiniz. Net bugünkü değeri elde etmek için, nakit akışlarının geri kalanından elde edilen NPV'ye ilk nakit akışını eklemeniz gerekir.

Aşağıdaki sonuçları alacaksınız -

Yılın Ortasında Nakit Akışı
Nakit akışlarının her yılın ortasında gerçekleştiğini varsayalım. Böyle bir durumda, net bugünkü değeri elde etmek için nakit akışlarından elde edilen NPV'yi $ \ sqrt {1 + r} $ ile çarpmanız gerekir.

Aşağıdaki sonuçları alacaksınız -

Düzensiz Aralıklarla Nakit Akışı
Düzensiz nakit akışlarıyla, yani rastgele zamanlarda oluşan nakit akışlarıyla net bugünkü değeri hesaplamak istiyorsanız, hesaplama biraz karmaşıktır.
Ancak Excel'de, XNPV işlevi ile böyle bir hesaplamayı kolayca yapabilirsiniz.
- Verilerinizi tarihler ve nakit akışlarıyla düzenleyin.
Note- Verilerinizdeki ilk tarih, tüm tarihlerin en eskisi olmalıdır. Diğer tarihler herhangi bir sırada olabilir.
- Net bugünkü değeri hesaplamak için XNPV işlevini kullanın.
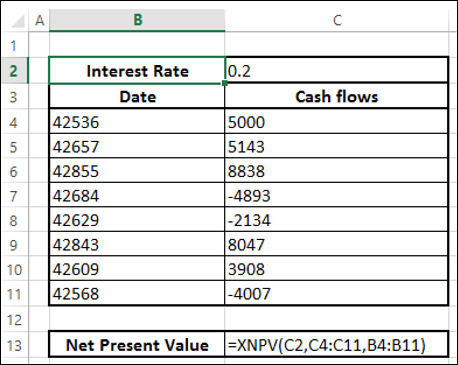
Aşağıdaki sonuçları alacaksınız -

Varsayalım bugünün tarihi 15 olduğunu inci gözlemlemek üzere Mart 2015, nakit akışının tüm tarihler sonradan tarihleri vardır. Bugün itibariyle net bugünkü değeri bulmak istiyorsanız, bunu üstteki verilere ekleyin ve nakit akışı için 0 belirtin.

Aşağıdaki sonuçları alacaksınız -

İç Getiri Oranı (IRR)
Bir yatırımın İç Getiri Oranı (IRR), NPV'nin 0 olduğu faiz oranıdır. Pozitif nakit akışlarının bugünkü değerlerinin negatif olanları tam olarak telafi ettiği oran değeridir. İskonto oranı IRR olduğunda, yatırım tamamen kayıtsızdır, yani yatırımcı para kazanmaz veya kaybetmez.
Aşağıdaki nakit akışlarını, farklı faiz oranlarını ve bunlara karşılık gelen NPV değerlerini göz önünde bulundurun.

Faiz oranı% 10 ile% 11 arasında gözlemleyebileceğiniz gibi NPV'nin işareti değişiyor. Faiz oranını% 10,53'e ayarladığınızda, NPV neredeyse 0 olur. Dolayısıyla, IRR% 10,53'tür.
Bir Proje için Nakit Akışlarının IRR'sini Belirleme
Excel fonksiyonu IRR ile nakit akışlarının IRR'sini hesaplayabilirsiniz.

IRR, önceki bölümde gördüğünüz gibi% 10.53'tür.
Verilen nakit akışları için IRR -
- var ve benzersiz
- var ve çoklu
- yok
Benzersiz IRR
IRR varsa ve benzersizse, birkaç olasılık arasından en iyi yatırımı seçmek için kullanılabilir.
İlk nakit akışı negatifse, yatırımcının paraya sahip olduğu ve yatırım yapmak istediği anlamına gelir. Daha sonra, IRR ne kadar yüksekse, yatırımcının aldığı faiz oranını temsil ettiği için o kadar iyidir.
İlk nakit akışı pozitifse, yatırımcının paraya ihtiyacı olduğu ve bir kredi aradığı anlamına gelir, IRR ne kadar düşükse, yatırımcının ödediği faiz oranını temsil ettiği için o kadar iyidir.
Bir IRR'nin benzersiz olup olmadığını bulmak için tahmin değerini değiştirin ve IRR'yi hesaplayın. IRR sabit kalırsa benzersizdir.

Gözlemlediğiniz gibi, IRR'nin farklı tahmin değerleri için benzersiz bir değeri vardır.

Çoklu IRR'ler
Bazı durumlarda, birden fazla IRR'niz olabilir. Aşağıdaki nakit akışlarını düşünün. IRR'yi farklı tahmin değerleriyle hesaplayın.

Aşağıdaki sonuçları alacaksınız -

İki IRR -% -9.59 ve% 216.09 olduğunu gözlemleyebilirsiniz. NPV'yi hesaplayan bu iki IRR'yi doğrulayabilirsiniz.

Hem -% 9,59 hem de% 216,09 için NPV 0'dır.
IRR yok
Bazı durumlarda IRR'niz olmayabilir. Aşağıdaki nakit akışlarını düşünün. IRR'yi farklı tahmin değerleriyle hesaplayın.

Tüm tahmin değerleri için sonucu #SAYI olarak alacaksınız.

Sonuç #SAYI, dikkate alınan nakit akışları için IRR olmadığı anlamına gelir.
Nakit Akış Modelleri ve IRR
Nakit akışlarında negatifden pozitife veya pozitiften negatife gibi yalnızca bir işaret değişikliği varsa, benzersiz bir IRR garanti edilir. Örneğin, sermaye yatırımlarında ilk nakit akışı negatif olurken, geri kalan nakit akışı pozitif olacaktır. Bu gibi durumlarda, benzersiz IRR vardır.
Nakit akışlarında birden fazla işaret değişikliği varsa, IRR mevcut olmayabilir. Var olsa bile benzersiz olmayabilir.
IRR'lere dayalı kararlar
Birçok analist IRR'yi kullanmayı tercih eder ve bu popüler bir karlılık ölçüsüdür çünkü yüzde olarak anlaşılması ve gerekli getiri ile karşılaştırılması kolaydır. Bununla birlikte, IRR ile karar verirken bazı sorunlar var. IRR'lerde derecelendirirseniz ve bu derecelere göre kararlar alırsanız, yanlış kararlar alabilirsiniz.
NPV'nin finansal kararlar almanızı sağlayacağını zaten görmüştünüz. Bununla birlikte, IRR ve NPV, projeler birbirini dışladığında her zaman aynı kararı vermeyecektir.
Mutually exclusive projectsbir projenin seçilmesinin diğerinin kabulünü engellediği projelerdir. Karşılaştırılan projeler birbirini dışladığında, NPV ve IRR arasında bir sıralama çatışması ortaya çıkabilir. Proje A ve proje B arasında seçim yapmanız gerekiyorsa, NPV A projesinin kabul edilmesini önerebilirken, IRR B projesini önerebilir.
NPV ve IRR arasındaki bu tür bir çatışma, aşağıdaki nedenlerden biri nedeniyle ortaya çıkabilir -
- Projeler çok farklı boyutlardadır veya
- Nakit akışlarının zamanlaması farklıdır.
Önemli büyüklük farkı olan projeler
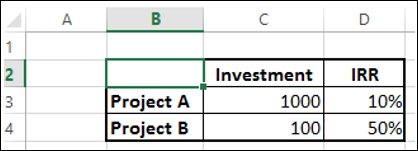
IRR ile bir karar vermek istiyorsanız, proje A 100 getiri ve Proje B 50 getiri sağlar. Dolayısıyla, proje A'ya yapılan yatırım karlı görünüyor. Ancak projelerin ölçeğindeki farklılık nedeniyle bu yanlış bir karardır.
Düşünün -
Yatırım yapacak 1000'iniz var.
1000'in tamamını A projesine yatırırsanız, 100 getiri elde edersiniz.
B projesine 100 yatırım yaparsanız, elinizde 900 olacak ve başka bir projeye, örneğin C projesine yatırım yapabileceksiniz. C projesinden% 20, sonra B ve C projesinden toplam getiri elde ettiğinizi varsayalım 230, kârlılıkta çok ileride.
Dolayısıyla, NPV bu gibi durumlarda karar vermenin daha iyi bir yoludur.
Farklı nakit akış zamanlamaları olan projeler

Yine, IRR'nin karar vereceğini düşünüyorsanız, B projesi seçim olacaktır. Bununla birlikte, proje A daha yüksek bir NBD'ye sahiptir ve ideal bir seçimdir.
Düzensiz Aralıklı Nakit Akışlarının IRR'si (XIRR)
Nakit akışlarınız bazen düzensiz aralıklarla olabilir. Böyle bir durumda, IRR eşit aralıklı zaman aralıkları gerektirdiğinden IRR'yi kullanamazsınız. Bunun yerine, nakit akışlarının yanı sıra nakit akışlarının tarihlerini de hesaba katan XIRR'yi kullanabilirsiniz.

İç Getiri Oranı% 26.42'dir.

Değiştirilmiş IRR (MIRR)
Finansman oranınızın yeniden yatırım oranınızdan farklı olduğu bir durumu düşünün. IRR ile İç Getiri Oranını hesaplarsanız, hem finans hem de yeniden yatırım için aynı oranı varsayar. Ayrıca, birden fazla IRR de alabilirsiniz.
Örneğin, aşağıda verilen nakit akışlarını düşünün -

Gözlemlediğiniz gibi, NPV bir kereden fazla 0'dır ve birden fazla IRR ile sonuçlanır. Ayrıca, yeniden yatırım oranı hesaba katılmaz. Bu gibi durumlarda, değiştirilmiş IRR (MIRR) kullanabilirsiniz.

Aşağıda gösterildiği gibi% 7'lik bir sonuç alacaksınız -

Note - IRR'nin aksine, MIRR her zaman benzersiz olacaktır.