Yetenek - Geometri
Nokta
Bir nokta tam bir konumdur
Çizgi segmenti
İki nokta A ve B arasındaki düz yola AB doğru parçası denir. Bir çizgi parçasının iki uç noktası vardır.

Ray
Bir doğru parçası AB'yi bir yönde sonsuza kadar uzatırken AB ışınını elde ederiz. Ray AB'nin A adında bir uç noktası vardır.

HAT
Her iki yönde sonsuza kadar uzanan AB doğru parçası AB çizgisi olarak adlandırılır.

Bir çizgi sonsuz sayıda nokta içerir.
Verilen noktalar aracılığıyla sonsuz sayıda çizgi çizilebilir.
Verilen iki A ve B noktasından geçmek için bir ve yalnızca bir çizgi çekilebilir.
Bir noktada iki çizgi buluşuyor.
İki uçak bir sırada buluşuyor.
Doğrusal
Verilen şekilde, A, B, C noktaları eşdoğrusaldır.

Eşzamanlı Hatlar
Aynı noktalarda kesişen üç veya daha fazla çizgiye eşzamanlı çizgiler denir.
Açı
Ortak uç noktaları O olan iki ışın OA ve OB, ∠AOB olarak yazılan AOB açısını oluşturur.

Açı Ölçüsü
OA'dan OB'ye dönüş miktarı, m olarak yazılan ∠AOB ölçüsü olarak adlandırılır (∠AOB).
360 ° açı
OA orijinal konumundan başlayan bir ışın OA, saat yönünün tersine O etrafında dönüyorsa ve tam bir dönüşten sonra orijinal konumuna geri dönerse, 360 ° döndüğünü söyleriz. Bu tam dönüş 360 ° eşit parçalara bölünür. Daha sonra her bölüme 1 derece denir ve 1 ° olarak yazılır
1 ° = 60 dakika, 60 'olarak yazılır
1 dakika = 60 saniye, 60 "olarak yazılır
Açı Türleri
Right angle - Ölçüsü 90 ° olan açıya dik açı denir.
Acute angle - Ölçüsü 90 ° 'den küçük olan açıya dar açı denir.
Obtuse angle - Ölçüsü 90 ° 'den fazla ancak 180 °' den az olan açıya obtues açısı denir.
Straight angle - Ölçüsü 180 ° olan açıya Düz açı denir.
Reflex angle - Ölçüsü 180 ° 'den fazla ancak 360 °' den küçük olan açıya Refleks açısı denir.
Complete angle - Ölçüsü 360 ° olan açıya tam açı denir.
Equal angle - Aynı ölçüye sahiplerse iki açının eşit olduğu söylenir.
Complementary angleÖlçülerinin toplamı 90 ise iki açının tamamlayıcı olduğu söylenir. Örneğin, 65 ° ve 25 ° 'lik açılar tamamlayıcı açıdır.
Supplementary angle- Ölçülerinin toplamı 180 ° ise iki açının tamamlayıcı olduğu söylenir. Örneğin, 70 ° ve 110 ° açı ölçüleri tamamlayıcıdır.
Adjacent angle- İki açı, aynı tepe noktasına ve ortak olmayan kollar ortak kolun her iki yanında olacak şekilde ortak bir kola sahipse bitişik açı olarak adlandırılır. Verilen şekilde, ∠AOC ve ∠BOC bitişik açıdır.

Önemli Sonuçlar
Bir ışın bir çizgi üzerinde duruyorsa, bu şekilde oluşturulan iki bitişik açının toplamı 180 ° 'dir. Verilen şekilde, ışın CP AB çizgisi üzerinde durur.

∴ ∠ACD + ∠BCD = 180°.
Doğru üzerinde belirli bir noktada bir doğrunun aynı tarafında oluşan tüm açıların toplamı 180 ° 'dir. Verilen şekilde, AOB'nin aynı tarafında dört açı oluşturulmuştur.

∴ ∠AOE + ∠EOD + ∠DOC + ∠COD = 180°.
Bir noktanın etrafındaki tüm açının toplamı 360 ° 'dir. Verilen şekilde bir O noktası etrafında beş açı oluşturulmuştur.

∴∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA=360°.
Dikey Karşıt Açılar
İki çizgi A Band CD bir O noktasında kesişirse, AOC, BOD ve BOC, AOD iki çift dikey olarak karşıt açıdır.
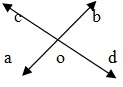
∴ ∠AOC = ∠BOD and ∠AOD = ∠BOC
Paralel çizgiler
İki çizgi aynı düzlemde uzanıyorsa ve her iki tarafta da üretildiğinde kesişmiyorsa, bu tür çizgilerin paralel olduğu söylenir ve L || m yazarız.
Paralel çizgileri kesen çapraz çizgi

İki paralel hat AB ve CD, enine bir EF ile kesilsin. Sonra
İlgili açı eşittir
(∠1 = ∠5), (∠4= ∠8 ), (∠2 = ∠6) , (∠3 = ∠7)Alternatif iç açılar eşittir.
(∠3 =∠5 ) and (∠4 =∠6 )Konsektif iç açılar tamamlayıcıdır
∠4+∠5 = 180° and ∠3 +∠6 = 180°.Üçgen
Üç düz çizgiyle sınırlanan şekle üçgen denir. Verilen şekilde, ∆ABC var; ∆ABC'nin üç köşesi A, B, C'dir. A, ∠B ve ∠C olmak üzere üç açıya sahiptir. AB, AC ve BC olmak üzere üç tarafı vardır.

Üçgen Türleri
Tüm kenarları eşit olan üçgene eşkenar üçgen denir.
İki kenarı eşit olan üçgene ikizkenar üçgen denir.
Tüm kenarları farklı uzunluklara sahip bir üçgene, skalen üçgeni denir.
Bir açısı 90 ° olan üçgene dik üçgen denir.
Bir açısı 90 ° ile 180 ° arasında olan üçgene geniş üçgen denir.
Her biri açısı dar olan üçgene akut üçgen denir.
Bir üçgenin tüm kenarlarının toplamına üçgenin çevresi denir.
Bir üçgenin iki kenarının toplamı üçüncü kenardan daha büyüktür.
∠B = 90 ° olan dik açılı bir ABC'de, AC 2 = AB 2 + BC 2'ye sahibiz . Buna Pisagor Teoremi denir.
Dörtgen
Dört düz çizgi ile sınırlanan bir şekle dörtgen denir. Bir dörtgenin tüm açılarının toplamı 360 ° 'dir.
Rectangle- Bir dörtgene, karşıt kenarı eşitse ve her bir açısı 90 ° ise dikdörtgen denir. Verilen şek. ABCD bir dikdörtgendir.

Square- Bir dörtgene, tüm kenarları eşitse ve açılarının her biri 90 ° ise kare olarak adlandırılır. Verilen şek. ABCD, AB = BC = CD = DA olduğu karedir.

Parallelogram- Bir dörtgene paralelkenar denir, eğer zıt tarafları paralel ise. Verilen şek. ABCD, AB = DC ve AD = BC olan bir paralelkenardır.

Rhombus- Tüm kenarları eşit olan bir paralelkenara eşkenar dörtgen denir. Verilen şek. ABCD, AB = BC = CD = DA, AB || DC ve AD || M.Ö.
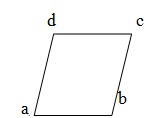
Önemli gerçekler
Bir dörtgen, karşıt kenarlar eşitse ve köşegenleri eşitse bir dikdörtgendir.
Dörtgen, tüm kenarlar eşitse ve köşegen eşitse Karedir.
Bir dörtgen, zıt taraflar eşitse bir paralelkenardır.
Bir dörtgen bir paralelkenardır, ancak karşıt kenarlar eşitse ancak köşegenler eşit değilse bir dikdörtgen değildir.
Dörtgen bir eşkenar dörtgendir ancak tüm kenarları eşitse ve köşegenler eşit değilse kare değildir.
Dörtgenle İlgili Sonuçlar
Paralelkenarda, elimizde
Zıt taraflar eşittir.
Zıt açılar eşittir.
Her bir köşegen paralelkenarı ikiye böler.
Bir paralelkenarın köşegenleri birbirini ikiye böler.
Bir dikdörtgenin köşegenleri eşittir.
Bir eşkenar dörtgenin köşegenleri birbirlerini dik açılarla ikiye böler.
Çemberdeki Sonuçlar

Merkezden bir akora dik olan, akoru ikiye böler.
Doğrusal olmayan üç noktadan geçen bir ve yalnızca bir daire vardır.
Yarım daire içindeki açı dik açıdır.
Döngüsel bir dörtgenin ters açıları tamamlayıcıdır.
Bir dairenin aynı kesimindeki açı eşittir.
Bir dairenin herhangi bir noktasındaki teğet, temas noktasından geçen yarıçapa diktir.
Bir çemberin dışındaki bir noktadan iki tanjant eşittir.
PT bir daireye teğet ise ve PAB bir sekant ise, O halde PA x PB = PT 2