Yakınsama Bölgesi (ROC)
Laplace dönüşümünün yakınsadığı σ değerinin aralık değişimine yakınsama bölgesi denir.
Laplace Dönüşümünün ROC'sinin Özellikleri
ROC, s-düzleminde jω eksenine paralel şerit çizgileri içerir.

Eğer x (t) mutlak integral ise ve sonlu süreli ise, o zaman ROC tüm s-düzlemidir.
Eğer x (t) sağ taraflı bir dizi ise, o zaman ROC: Re {s}> σ o .
Eğer x (t) bir sol taraflı dizi ise, o zaman ROC: Re {s} <σ o .
X (t) iki taraflı bir sekans ise, o zaman ROC iki bölgenin kombinasyonudur.
ROC, aşağıda verilen örneklerden yararlanılarak açıklanabilir:
Example 1: Find the Laplace transform and ROC of $x(t) = e-^{at}u(t)$
$ LT [x (t)] = LT [e - ^ {at} u (t)] = {1 \ S + a} $ üzerinden
$ Re {} \ gt -a $
$ ROC: Re {s} \ gt> -a $

Example 2: Find the Laplace transform and ROC of $x(t) = e^{at}u(-t)$
$ LT [x (t)] = LT [e ^ {at} u (t)] = {1 \ Sa} $ üzerinden
$ Re {s} <a $
$ ROC: Re {s} <a $

Example 3: Find the Laplace transform and ROC of $x(t) = e^{-at}u(t)+e^{at}u(-t)$
$ LT [x (t)] = LT [e ^ {- at} u (t) + e ^ {at} u (-t)] = {1 \ over S + a} + {1 \ over Sa} $
$ {1 \ over S + a} Re \ {s \} \ gt -a $ için
$ {1 \ over Sa} Re \ {s \} \ lt a $ için

Yukarıdaki diyagrama bakıldığında, kombinasyon bölgesi –a'dan a'ya uzanır. Bu nedenle
$ ROC: -a <Re {s} <a $
Nedensellik ve İstikrar
Bir sistemin nedensel olması için, transfer fonksiyonunun tüm kutupları s-düzleminin sağ yarısı olmalıdır.

Bir sistemin, transfer fonksiyonunun tüm kutupları s-düzleminin sol yarısında yattığı zaman kararlı olduğu söylenir.

Transfer fonksiyonunun en az bir kutbu s-düzleminin sağ yarısına kaydırıldığında bir sistemin kararsız olduğu söylenir.
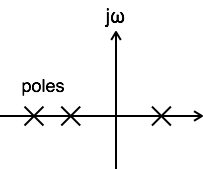
Bir sistemin, transfer fonksiyonunun en az bir kutbu s-düzleminin jω ekseninde olması durumunda marjinal olarak kararlı olduğu söylenir.

Temel İşlevlerin ROC'si
| f (t) | F (ler) | ROC |
|---|---|---|
| $ u (t) $ | $$ {1 \ over s} $$ | ROC: Re {s}> 0 |
| $ t \, u (t) $ | $ {1 \ over s ^ 2} $$ | ROC: Re {s}> 0 |
| $ t ^ n \, u (t) $ | $$ {n! \ over s ^ {n + 1}} $$ | ROC: Re {s}> 0 |
| $ e ^ {at} \, u (t) $ | $$ {1 \ over sa} $$ | ROC: Re {s}> a |
| $ e ^ {- at} \, u (t) $ | $$ {1 \ over s + a} $$ | ROC: Re {s}> -a |
| $ e ^ {at} \, u (t) $ | $$ - {1 \ over sa} $$ | ROC: Re {s} <a |
| $ e ^ {- at} \, u (-t) $ | $$ - {1 \ over s + a} $$ | ROC: Re {s} <-a |
| $ t \, e ^ {at} \, u (t) $ | $$ {1 \ over (sa) ^ 2} $$ | ROC: Re {s}> a |
| $ t ^ {n} e ^ {at} \, u (t) $ | $$ {n! \ over (sa) ^ {n + 1}} $$ | ROC: Re {s}> a |
| $ t \, e ^ {- at} \, u (t) $ | $$ {1 \ over (s + a) ^ 2} $$ | ROC: Re {s}> -a |
| $ t ^ n \, e ^ {- at} \, u (t) $ | $$ {n! \ over (s + a) ^ {n + 1}} $$ | ROC: Re {s}> -a |
| $ t \, e ^ {at} \, u (-t) $ | $$ - {1 \ over (sa) ^ 2} $$ | ROC: Re {s} <a |
| $ t ^ n \, e ^ {at} \, u (-t) $ | $$ - {n! \ over (sa) ^ {n + 1}} $$ | ROC: Re {s} <a |
| $ t \, e ^ {- at} \, u (-t) $ | $$ - {1 \ over (s + a) ^ 2} $$ | ROC: Re {s} <-a |
| $ t ^ n \, e ^ {- at} \, u (-t) $ | $$ - {n! \ over (s + a) ^ {n + 1}} $$ | ROC: Re {s} <-a |
| $ e ^ {- at} \ cos \, bt $ | $$ {s + a \ over (s + a) ^ 2 + b ^ 2} $$ | |
| $ e ^ {- at} \ sin \, bt $ | $$ {b \ over (s + a) ^ 2 + b ^ 2} $$ |