Sinyaller Temel Türler
İşte birkaç temel sinyal:
Birim Adım İşlevi
Birim adım işlevi, u (t) ile gösterilir. U (t) = $ \ left \ {\ begin {matrix} 1 & t \ geqslant 0 \\ 0 & t <0 \ end {matrix} \ right olarak tanımlanır. $

- En iyi test sinyali olarak kullanılır.
- Birim adım fonksiyonu altındaki alan birliktir.
Unit Impulse İşlevi
Dürtü fonksiyonu δ (t) ile gösterilir. ve δ (t) = $ \ left \ {\ begin {matrix} 1 & t = 0 \\ 0 & t \ neq 0 \ end {matrix} \ right olarak tanımlanır. $

$$ \ int _ {- \ infty} ^ {\ infty} δ (t) dt = u (t) $$
$$ \ delta (t) = {du (t) \ over dt} $$
Rampa Sinyali
Rampa sinyali r (t) ile gösterilir ve r (t) = $ \ left \ {\ begin {matrix} t & t \ geqslant 0 \\ 0 & t <0 \ end {matrix} \ right olarak tanımlanır . $

$$ \ int u (t) = \ int 1 = t = r (t) $$
$$ u (t) = {dr (t) \ over dt} $$
Birim rampanın altındaki alan birliktir.
Parabolik Sinyal
Parabolik sinyal x (t) = $ \ left \ {\ begin {matrix} t ^ 2/2 & t \ geqslant 0 \\ 0 & t <0 \ end {matrix} \ right olarak tanımlanabilir. $
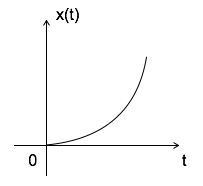
$$ \ iint u (t) dt = \ int r (t) dt = \ int t dt = {t ^ 2 \ over 2} = parabolik sinyal $$
$$ \ Rightarrow u (t) = {d ^ 2x (t) \ over dt ^ 2} $$
$$ \ Rightarrow r (t) = {dx (t) \ over dt} $$
Signum İşlevi
Signum işlevi sgn (t) olarak belirtilir. Sgn (t) = $ \ left \ {\ begin {matrix} 1 & t> 0 \\ 0 & t = 0 \\ -1 & t <0 \ end {matrix} \ right olarak tanımlanır. $

Üstel Sinyal
Üstel sinyal x (t) = $ e ^ {\ alpha t} $ biçimindedir.
Üstel biçim, $ \ alpha $ ile tanımlanabilir.
Case i: $ \ alpha $ = 0 $ \ ile $ x (t) = $ e ^ 0 $ = 1 ise

Case ii:$ \ alpha $ <0 ie -ve ise x (t) = $ e ^ {- \ alpha t} $. Şekle azalan üstel denir.

Case iii:$ \ alpha $> 0 ie + ve ise x (t) = $ e ^ {\ alpha t} $. Şekle yükseltme üstel denir.

Dikdörtgen Sinyal
X (t) olarak gösterilsin ve şu şekilde tanımlanır:

Üçgen Sinyal
X (t) olarak gösterilsin

Sinüzoidal Sinyal
Sinüzoidal sinyal x (t) = A cos ($ {w} _ {0} \, \ pm \ phi $) veya A sin ($ {w} _ {0} \, \ pm \ phi $ biçimindedir. )
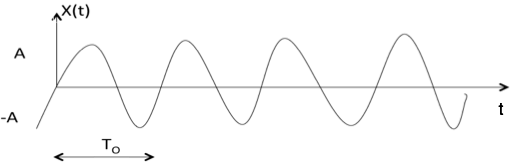
Burada T 0 = 2 $ \ pi \ over {w} _ {0} $
Sinc İşlevi
Sinc (t) olarak belirtilir ve sinc olarak tanımlanır.
$$ (t) = {sin \ pi t \ over \ pi t} $$
$$ = 0 \, \ text {t için} = \ pm 1, \ pm 2, \ pm 3 ... $$

Örnekleme İşlevi
Sa (t) olarak belirtilir ve şu şekilde tanımlanır:
$$ sa (t) = {sin t \ over t} $$
$$ = 0 \, \, \ text {t için} = \ pm \ pi, \, \ pm 2 \ pi, \, \ pm 3 \ pi \, ... $$
