Z-Dönüşümleri Özellikleri
Z-Dönüşümü aşağıdaki özelliklere sahiptir:
Doğrusallık Özelliği
$ \, X (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $ ise
ve $ \, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} Y (Z) $
Daha sonra doğrusallık özelliği şunu belirtir:
$ a \, x (n) + b \, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} a \, X (Z) + b \, Y (Z) $
Zaman Kaydıran Özellik
$ \, X (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $ ise
Sonra Zaman kaydırma özelliği şunu belirtir:
$ x (nm) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} z ^ {- m} X (Z) $
Üstel Sıra Özelliği ile Çarpma
$ \, X (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $ ise
Daha sonra üstel bir dizi özelliği ile çarpma,
$ a ^ n \,. x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z / a) $
Zaman Tersine Çevirme Özelliği
$ \, X (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $ ise
Sonra zamanın tersine çevrilmesi özelliği şunu belirtir:
$ x (-n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (1 / Z) $
Z Alanında Farklılaşma VEYA n Özelliğe Göre Çarpma
$ \, X (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $ ise
Daha sonra n ile çarpma veya z-alanı özelliğindeki farklılaşma şunu belirtir:
$ n ^ kx (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} [-1] ^ kz ^ k {d ^ k X (Z) \ over dZ ^ K} $
Evrişim Özelliği
$ \, X (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $ ise
ve $ \, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} Y (Z) $
Sonra evrişim özelliği şunu belirtir:
$ x (n) * y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) .Y (Z) $
Korelasyon Özelliği
$ \, X (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $ ise
ve $ \, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} Y (Z) $
Daha sonra korelasyon özelliği şunu belirtir:
$ x (n) \ otimes y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) .Y (Z ^ {- 1}) $
İlk Değer ve Son Değer Teoremleri
Z-dönüşümünün başlangıç değeri ve son değer teoremleri nedensel sinyal için tanımlanmıştır.
Başlangıç Değer Teoremi
Nedensel bir sinyal x (n) için, başlangıç değer teoremi şunu belirtir:
$ x (0) = \ lim_ {z \ ila \ infty} X (z) $
Bu, ters z-dönüşümü almadan sinyalin başlangıç değerini bulmak için kullanılır.
Nihai Değer Teoremi
Nedensel bir sinyal x (n) için, nihai değer teoremi şunu belirtir:
$ x (\ infty) = \ lim_ {z \ ila 1} [z-1] X (z) $
Bu, ters z-dönüşümü almadan sinyalin son değerini bulmak için kullanılır.
Z-Dönüşümünün Yakınsama Bölgesi (ROC)
Z-dönüşümünün yakınsadığı z'nin varyasyon aralığı, z-dönüşümünün yakınsama bölgesi olarak adlandırılır.
Z-Dönüşümlerinin ROC'sinin Özellikleri
Z-dönüşümünün ROC'si, z-düzleminde daire ile gösterilir.
ROC herhangi bir kutup içermez.
X (n), sonlu süreli bir nedensel dizi veya sağ taraflı bir dizi ise, o zaman ROC, z = 0 haricinde tüm z düzlemidir.
X (n), sonlu süreli bir nedensiz dizi veya sol taraftaki bir dizi ise, bu durumda ROC, z = ∞ haricinde tüm z düzlemidir.
Eğer x (n) sonsuz süreli bir nedensel dizi ise, ROC yarıçapı aie | z | > a.
Eğer x (n) sonsuz süreli bir anti-nedensel dizi ise, ROC yarıçapı aie | z | <a.
X (n), sonlu süreli iki taraflı bir dizi ise, o zaman ROC, z = 0 ve z = ∞ haricinde tüm z düzlemidir.
ROC kavramı aşağıdaki örnekle açıklanabilir:
Example 1: $ A ^ nu [n] + a ^ {-} nu [-n-1] $ z-dönüşümünü ve ROC'sini bulun
$ ZT [a ^ nu [n]] + ZT [a ^ {- n} u [-n-1]] = {Z \ za üzerinden} + {Z \ Z üzerinden {-1 \ a}} $
$$ ROC: | z | \ gt a \ quad \ quad ROC: | z | \ lt {1 \ over a} $$
ROC'nin grafiği, a> 1 ve a <1 olmak üzere iki koşula sahiptir, çünkü a.

Bu durumda, ROC kombinasyonu yoktur.
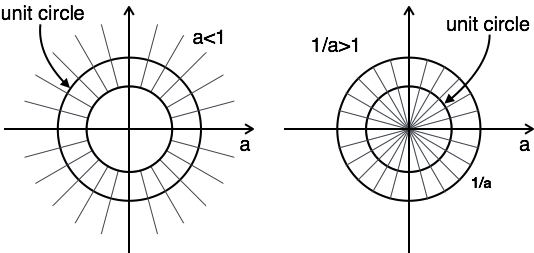
Burada, ROC kombinasyonu $ a \ lt | z | \ lt {1 \ a} $ üzerinden
Dolayısıyla bu problem için, a <1 olduğunda z-dönüşümü mümkündür.
Nedensellik ve İstikrar
Ayrık zamanlı LTI sistemleri için nedensellik koşulu aşağıdaki gibidir:
Ayrık zamanlı bir LTI sistemi,
ROC en dıştaki kutbun dışında.
Transfer fonksiyonunda H [Z], pay sırası paydanın sırasından daha büyük olamaz.
Ayrık Zamanlı LTI Sistemleri için Kararlılık Koşulu
Ayrık bir LTI sistemi ne zaman kararlıdır?
sistem işlevi H [Z] birim çemberi içerir | z | = 1.
transfer fonksiyonunun tüm kutupları birim çember | z | = 1 içinde uzanır.
Temel Sinyallerin Z Dönüşümü
| x (t) | X [Z] |
|---|---|
| $ \ delta $ | 1 |
| $ u (n) $ | $ {Z \ over Z-1} $ |
| $ u (-n-1) $ | $ - {Z \ over Z-1} $ |
| $ \ delta (nm) $ | $ z ^ {- m} $ |
| $ a ^ nu [n] $ | Za} $ üzerinden $ {Z \ |
| $ a ^ nu [-n-1] $ | $ - {Z \ over Za} $ |
| $ n \, a ^ nu [n] $ | $ {aZ \ over | Za | ^ 2} $ |
| $ n \, a ^ nu [-n-1] $ | $ - {aZ \ over | Za | ^ 2} $ |
| $ a ^ n \ cos \ omega nu [n] $ | $ {Z ^ 2-aZ \ cos \ omega \ over Z ^ 2-2aZ \ cos \ omega + a ^ 2} $ |
| $ a ^ n \ sin \ omega nu [n] $ | $ {aZ \ sin \ omega \ over Z ^ 2 -2aZ \ cos \ omega + a ^ 2} $ |