Hệ thống điều khiển - Lô Bode
Biểu đồ Bode hoặc biểu đồ Bode bao gồm hai biểu đồ -
- Biểu đồ độ lớn
- Cốt truyện giai đoạn
Trong cả hai biểu đồ, trục x đại diện cho tần số góc (thang logarit). Trong khi đó, yaxis biểu thị độ lớn (thang tuyến tính) của hàm truyền vòng hở trong biểu đồ độ lớn và góc pha (thang tuyến tính) của hàm truyền vòng mở trong biểu đồ pha.
Các magnitude của hàm truyền vòng hở tính bằng dB là -
$$ M = 20 \: \ log | G (j \ omega) H (j \ omega) | $$
Các phase angle của hàm truyền vòng hở theo độ là -
$$ \ phi = \ angle G (j \ omega) H (j \ omega) $$
Note - Cơ số của lôgarit là 10.
Cơ bản về lô Bode
Bảng sau đây cho thấy độ dốc, độ lớn và các giá trị góc pha của các số hạng có trong hàm truyền vòng hở. Dữ liệu này rất hữu ích trong khi vẽ biểu đồ Bode.
| Loại điều khoản | G (jω) H (jω) | Độ dốc (dB / dec) | Độ lớn (dB) | Góc pha (độ) |
|---|---|---|---|---|
Không thay đổi |
$ K $ |
$ 0 $ |
$ 20 \ log K $ |
$ 0 $ |
0 tại điểm gốc |
$ j \ omega $ |
$ 20 $ |
$ 20 \ log \ omega $ |
$ 90 $ |
số không 'n' tại gốc |
$ (j \ omega) ^ n $ |
$ 20 \: n $ |
$ 20 \: n \ log \ omega $ |
$ 90 \: n $ |
Cực tại nguồn gốc |
$ \ frac {1} {j \ omega} $ |
$ -20 $ |
$ -20 \ log \ omega $ |
$ -90 \: hoặc \: 270 $ |
cực 'n' tại điểm gốc |
$ \ frac {1} {(j \ omega) ^ n} $ |
$ -20 \: n $ |
$ -20 \: n \ log \ omega $ |
$ -90 \: n \: hoặc \: 270 \: n $ |
Số 0 đơn giản |
$ 1 + j \ omega r $ |
$ 20 $ |
$ 0 \: cho \: \ omega <\ frac {1} {r} $ $ 20 \: \ log \ omega r \: for \: \ omega> \ frac {1} {r} $ |
$ 0 \: cho \: \ omega <\ frac {1} {r} $ $ 90 \: cho \: \ omega> \ frac {1} {r} $ |
Cực đơn giản |
$ \ frac {1} {1 + j \ omega r} $ |
$ -20 $ |
$ 0 \: cho \: \ omega <\ frac {1} {r} $ $ -20 \: \ log \ omega r \: for \: \ omega> \ frac {1} {r} $ |
$ 0 \: cho \: \ omega <\ frac {1} {r} $ $ -90 \: hoặc \: 270 \: cho \: \ omega> \ frac {1} {r} $ |
Thuật ngữ phái sinh bậc hai |
$ \ omega_n ^ 2 \ left (1- \ frac {\ omega ^ 2} {\ omega_n ^ 2} + \ frac {2j \ delta \ omega} {\ omega_n} \ right) $ |
$ 40 $ |
$ 40 \: \ log \: \ omega_n \: cho \: \ omega <\ omega_n $ $ 20 \: \ log \ :( 2 \ delta \ omega_n ^ 2) \: cho \: \ omega = \ omega_n $ $ 40 \: \ log \: \ omega \: cho \: \ omega> \ omega_n $ |
$ 0 \: cho \: \ omega <\ omega_n $ $ 90 \: cho \: \ omega = \ omega_n $ $ 180 \: cho \: \ omega> \ omega_n $ |
Số hạng tích phân bậc hai |
$ \ frac {1} {\ omega_n ^ 2 \ left (1- \ frac {\ omega ^ 2} {\ omega_n ^ 2} + \ frac {2j \ delta \ omega} {\ omega_n} \ right)} $ |
$ -40 $ |
$ -40 \: \ log \: \ omega_n \: cho \: \ omega <\ omega_n $ $ -20 \: \ log \ :( 2 \ delta \ omega_n ^ 2) \: cho \: \ omega = \ omega_n $ $ -40 \: \ log \: \ omega \: cho \: \ omega> \ omega_n $ |
$ -0 \: cho \: \ omega <\ omega_n $ $ -90 \: cho \: \ omega = \ omega_n $ $ -180 \: cho \: \ omega> \ omega_n $ |
Xét hàm truyền vòng mở $ G (s) H (s) = K $.
Độ lớn $ M = 20 \: \ log K $ dB
Góc pha $ \ phi = 0 $ độ
Nếu $ K = 1 $ thì cường độ là 0 dB.
Nếu $ K> 1 $, thì độ lớn sẽ là dương.
Nếu $ K <1 $, thì độ lớn sẽ âm.
Hình sau cho thấy biểu đồ Bode tương ứng.


Biểu đồ độ lớn là một đường nằm ngang, không phụ thuộc vào tần số. Đường 0 dB chính là đồ thị cường độ khi giá trị của K là một. Đối với các giá trị dương của K, đường ngang sẽ dịch chuyển $ 20 \: \ log K $ dB lên trên đường 0 dB. Đối với các giá trị âm của K, đường ngang sẽ dịch chuyển $ 20 \: \ log K $ dB xuống dưới đường 0 dB. Đường 0 độ chính là đồ thị pha cho tất cả các giá trị dương của K.
Xét hàm truyền vòng lặp mở $ G (s) H (s) = s $.
Độ lớn $ M = 20 \ log \ omega $ dB
Góc pha $ \ phi = 90 ^ 0 $
Tại $ \ omega = 0,1 $ rad / giây, cường độ là -20 dB.
Tại $ \ omega = 1 $ rad / giây, cường độ là 0 dB.
Tại $ \ omega = 10 $ rad / giây, cường độ là 20 dB.
Hình sau cho thấy biểu đồ Bode tương ứng.


Biểu đồ cường độ là một đường, có độ dốc 20 dB / tháng mười. Đường này bắt đầu tại $ \ omega = 0,1 $ rad / giây có cường độ -20 dB và nó tiếp tục trên cùng một độ dốc. Nó đang chạm vào vạch 0 dB tại $ \ omega = 1 $ rad / giây. Trong trường hợp này, đồ thị pha là dòng 90 0 .
Xem xét hàm truyền vòng lặp mở $ G (s) H (s) = 1 + s \ tau $.
Độ lớn $ M = 20 \: log \ sqrt {1 + \ omega ^ 2 \ tau ^ 2} $ dB
Góc pha $ \ phi = \ tan ^ {- 1} \ omega \ tau $ độ
Đối với $ ω <\ frac {1} {\ tau} $, cường độ là 0 dB và góc pha là 0 độ.
Đối với $ \ omega> \ frac {1} {\ tau} $, độ lớn là $ 20 \: \ log \ omega \ tau $ dB và góc pha là 90 0 .
Hình sau cho thấy biểu đồ Bode tương ứng.

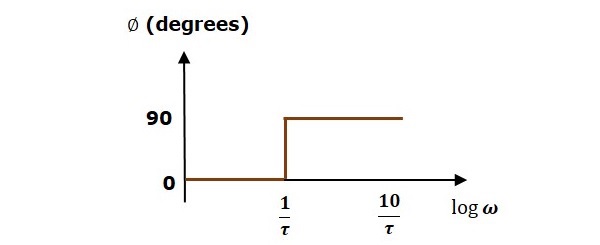
Biểu đồ cường độ có cường độ 0 dB tối đa $ \ omega = \ frac {1} {\ tau} $ rad / giây. Từ $ \ omega = \ frac {1} {\ tau} $ rad / giây, nó đang có độ dốc 20 dB / dec. Trong trường hợp này, biểu đồ pha có góc pha 0 độ lên đến $ \ omega = \ frac {1} {\ tau} $ rad / giây và từ đây, nó có góc pha là 90 0 . Biểu đồ Bode này được gọi làasymptotic Bode plot.
Vì độ lớn và các biểu đồ pha được biểu diễn bằng các đường thẳng, nên các biểu đồ Bode Chính xác giống với các biểu đồ Bode tiệm cận. Sự khác biệt duy nhất là các ô Exact Bode sẽ có các đường cong đơn giản thay vì các đường thẳng.
Tương tự, bạn có thể vẽ biểu đồ Bode cho các điều khoản khác của hàm truyền vòng lặp mở được đưa ra trong bảng.