Phản hồi của Hệ thống đặt hàng đầu tiên
Trong chương này, chúng ta hãy thảo luận về phản ứng thời gian của hệ thống bậc nhất. Hãy xem xét sơ đồ khối sau của hệ thống điều khiển vòng kín. Ở đây, một hàm truyền vòng lặp mở, $ \ frac {1} {sT} $ được kết nối với một phản hồi tiêu cực thống nhất.

Chúng tôi biết rằng chức năng truyền của hệ thống điều khiển vòng kín có phản hồi tiêu cực thống nhất như,
$$ \ frac {C (s)} {R (s)} = \ frac {G (s)} {1 + G (s)} $$
Thay thế, $ G (s) = \ frac {1} {sT} $ trong phương trình trên.
$$ \ frac {C (s)} {R (s)} = \ frac {\ frac {1} {sT}} {1+ \ frac {1} {sT}} = \ frac {1} {sT + 1} $$
Lũy thừa của s là một ở mẫu số. Do đó, hàm truyền ở trên là bậc nhất và hệ thống được cho làfirst order system.
Chúng ta có thể viết lại phương trình trên dưới dạng
$$ C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s) $$
Ở đâu,
C(s) là biến đổi Laplace của tín hiệu đầu ra c (t),
R(s) là biến đổi Laplace của tín hiệu đầu vào r (t), và
T là hằng số thời gian.
Làm theo các bước sau để nhận phản hồi (đầu ra) của hệ thống bậc nhất trong miền thời gian.
Thực hiện phép biến đổi Laplace của tín hiệu đầu vào $ r (t) $.
Hãy xem xét phương trình, $ C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s) $
Thay giá trị $ R (s) $ vào phương trình trên.
Làm phân số từng phần của $ C (s) $ nếu được yêu cầu.
Áp dụng phép biến đổi Laplace ngược cho $ C (s) $.
Trong chương trước, chúng ta đã thấy các tín hiệu kiểm tra tiêu chuẩn như xung, bước, đoạn đường nối và parabol. Bây giờ chúng ta hãy tìm hiểu các phản hồi của hệ thống đặt hàng đầu tiên cho từng đầu vào, từng cái một. Tên của phản hồi được đưa ra theo tên của tín hiệu đầu vào. Ví dụ, đáp ứng của hệ thống đối với đầu vào xung được gọi là đáp ứng xung.
Phản ứng xung động của hệ thống đặt hàng đầu tiên
Xem xét unit impulse signal như một đầu vào cho hệ thống đặt hàng đầu tiên.
Vì vậy, $ r (t) = \ delta (t) $
Áp dụng phép biến đổi Laplace trên cả hai mặt.
$ R (s) = 1 $
Hãy xem xét phương trình, $ C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s) $
Thay thế, $ R (s) = 1 $ trong phương trình trên.
$$ C (s) = \ left (\ frac {1} {sT + 1} \ right) (1) = \ frac {1} {sT + 1} $$
Sắp xếp lại phương trình trên theo một trong các dạng chuẩn của phép biến đổi Laplace.
$$ C (s) = \ frac {1} {T \ left (\ s + \ frac {1} {T} \ right)} \ Rightarrow C (s) = \ frac {1} {T} \ left (\ frac {1} {s + \ frac {1} {T}} \ right) $$
Áp dụng phép biến đổi Laplace ngược cho cả hai phía.
$$ c (t) = \ frac {1} {T} e ^ \ left ({- \ frac {t} {T}} \ right) u (t) $$
Đáp ứng xung đơn vị được hiển thị trong hình sau.
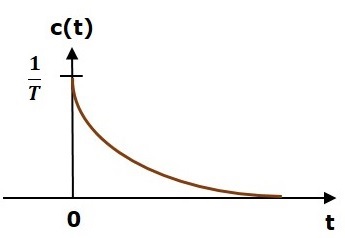
Các unit impulse response, c (t) là tín hiệu giảm dần theo cấp số nhân cho các giá trị dương của 't' và nó bằng 0 đối với các giá trị âm của 't'.
Phản hồi bước của hệ thống đặt hàng đầu tiên
Xem xét unit step signal như một đầu vào cho hệ thống đặt hàng đầu tiên.
Vì vậy, $ r (t) = u (t) $
Áp dụng phép biến đổi Laplace trên cả hai mặt.
$$ R (s) = \ frac {1} {s} $$
Hãy xem xét phương trình, $ C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s) $
Thay thế, $ R (s) = \ frac {1} {s} $ trong phương trình trên.
$$ C (s) = \ left (\ frac {1} {sT + 1} \ right) \ left (\ frac {1} {s} \ right) = \ frac {1} {s \ left (sT + 1 \ right)} $$
Làm phân số từng phần của C (s).
$$ C (s) = \ frac {1} {s \ left (sT + 1 \ right)} = \ frac {A} {s} + \ frac {B} {sT + 1} $$
$$ \ Rightarrow \ frac {1} {s \ left (sT + 1 \ right)} = \ frac {A \ left (sT + 1 \ right) + Bs} {s \ left (sT + 1 \ right)} $$
Ở cả hai phía, mẫu số là như nhau. Vì vậy, họ sẽ bị hủy bỏ bởi nhau. Do đó, cân bằng các số hạng tử số.
$$ 1 = A \ left (sT + 1 \ right) + Bs $$
Bằng cách cân bằng các số hạng không đổi ở cả hai vế, bạn sẽ nhận được A = 1.
Thay thế, A = 1 và tương đương với hệ số của s điều khoản của cả hai bên.
$$ 0 = T + B \ Rightarrow B = -T $$
Thay thế, A = 1 và B = −T trong khai triển một phần của $ C (s) $.
$$ C (s) = \ frac {1} {s} - \ frac {T} {sT + 1} = \ frac {1} {s} - \ frac {T} {T \ left (s + \ frac { 1} {T} \ right)} $$
$$ \ Rightarrow C (s) = \ frac {1} {s} - \ frac {1} {s + \ frac {1} {T}} $$
Áp dụng phép biến đổi Laplace ngược trên cả hai mặt.
$$ c (t) = \ left (1-e ^ {- \ left (\ frac {t} {T} \ right)} \ right) u (t) $$
Các unit step response, c (t) có cả điều khoản trạng thái nhất thời và trạng thái dừng.
Thuật ngữ tạm thời trong phản ứng bước đơn vị là -
$$ c_ {tr} (t) = - e ^ {- \ left (\ frac {t} {T} \ right)} u (t) $$
Thuật ngữ trạng thái ổn định trong phản ứng bước đơn vị là -
$$ c_ {ss} (t) = u (t) $$
Hình sau đây cho thấy phản ứng bước đơn vị.

Giá trị của unit step response, c(t)bằng 0 tại t = 0 và với mọi giá trị âm của t. Nó đang tăng dần từ giá trị 0 và cuối cùng đạt đến một ở trạng thái ổn định. Vì vậy, giá trị trạng thái ổn định phụ thuộc vào độ lớn của đầu vào.
Phản hồi của hệ thống đơn hàng đầu tiên
Xem xét unit ramp signal như một đầu vào cho hệ thống đặt hàng đầu tiên.
$ Vì vậy, r (t) = tu (t) $
Áp dụng phép biến đổi Laplace trên cả hai mặt.
$$ R (s) = \ frac {1} {s ^ 2} $$
Hãy xem xét phương trình, $ C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s) $
Thay thế, $ R (s) = \ frac {1} {s ^ 2} $ trong phương trình trên.
$$ C (s) = \ left (\ frac {1} {sT + 1} \ right) \ left (\ frac {1} {s ^ 2} \ right) = \ frac {1} {s ^ 2 ( sT + 1)} $$
Làm phân số từng phần của $ C (s) $.
$$ C (s) = \ frac {1} {s ^ 2 (sT + 1)} = \ frac {A} {s ^ 2} + \ frac {B} {s} + \ frac {C} {sT +1} $$
$$ \ Rightarrow \ frac {1} {s ^ 2 (sT + 1)} = \ frac {A (sT + 1) + Bs (sT + 1) + Cs ^ 2} {s ^ 2 (sT + 1) } $$
Ở cả hai phía, mẫu số là như nhau. Vì vậy, họ sẽ bị hủy bỏ bởi nhau. Do đó, cân bằng các số hạng tử số.
$$ 1 = A (sT + 1) + Bs (sT + 1) + Cs ^ 2 $$
Bằng cách cân bằng các số hạng không đổi ở cả hai vế, bạn sẽ nhận được A = 1.
Thay thế, A = 1 và cân bằng hệ số của s số hạng ở cả hai phía.
$$ 0 = T + B \ Rightarrow B = -T $$
Tương tự, thay B = −T và cân bằng hệ số của $ s ^ 2 $ số hạng trên cả hai vế. Bạn sẽ nhận được $ C = T ^ 2 $.
Thay A = 1, B = −T và $ C = T ^ 2 $ trong khai triển phân số từng phần của $ C (s) $.
$$ C (s) = \ frac {1} {s ^ 2} - \ frac {T} {s} + \ frac {T ^ 2} {sT + 1} = \ frac {1} {s ^ 2} - \ frac {T} {s} + \ frac {T ^ 2} {T \ left (s + \ frac {1} {T} \ right)} $$
$$ \ Rightarrow C (s) = \ frac {1} {s ^ 2} - \ frac {T} {s} + \ frac {T} {s + \ frac {1} {T}} $$
Áp dụng phép biến đổi Laplace ngược trên cả hai mặt.
$$ c (t) = \ left (t-T + Te ^ {- \ left (\ frac {t} {T} \ right)} \ right) u (t) $$
Các unit ramp response, c (t) có cả điều khoản trạng thái nhất thời và trạng thái dừng.
Thuật ngữ tạm thời trong phản hồi đoạn đường nối đơn vị là -
$$ c_ {tr} (t) = Te ^ {- \ left (\ frac {t} {T} \ right)} u (t) $$
Thuật ngữ trạng thái ổn định trong phản ứng dốc đơn vị là -
$$ c_ {ss} (t) = (tT) u (t) $$
Hình sau đây cho thấy phản ứng của đoạn đường nối đơn vị.

Các unit ramp response, c (t) theo sau tín hiệu đầu vào dốc đơn vị cho tất cả các giá trị dương của t. Tuy nhiên, có sự sai lệch của T đơn vị so với tín hiệu đầu vào.
Đáp ứng parabol của hệ thống đơn hàng đầu tiên
Xem xét unit parabolic signal như một đầu vào cho hệ thống đặt hàng đầu tiên.
Vì vậy, $ r (t) = \ frac {t ^ 2} {2} u (t) $
Áp dụng phép biến đổi Laplace trên cả hai mặt.
$$ R (s) = \ frac {1} {s ^ 3} $$
Hãy xem xét phương trình, $ C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s) $
Thay $ R (s) = \ frac {1} {s ^ 3} $ vào phương trình trên.
$$ C (s) = \ left (\ frac {1} {sT + 1} \ right) \ left (\ frac {1} {s ^ 3} \ right) = \ frac {1} {s ^ 3 ( sT + 1)} $$
Làm phân số từng phần của $ C (s) $.
$$ C (s) = \ frac {1} {s ^ 3 (sT + 1)} = \ frac {A} {s ^ 3} + \ frac {B} {s ^ 2} + \ frac {C} {s} + \ frac {D} {sT + 1} $$
Sau khi đơn giản hóa, bạn sẽ nhận được các giá trị của A, B, C và D lần lượt là 1, $ -T, \: T ^ 2 \: và \: −T ^ 3 $. Thay thế các giá trị này trong khai triển từng phần ở trên của (các) C.
$ C (s) = \ frac {1} {s ^ 3} - \ frac {T} {s ^ 2} + \ frac {T ^ 2} {s} - \ frac {T ^ 3} {sT + 1 } \: \ Rightarrow C (s) = \ frac {1} {s ^ 3} - \ frac {T} {s ^ 2} + \ frac {T ^ 2} {s} - \ frac {T ^ 2} {s + \ frac {1} {T}} $
Áp dụng phép biến đổi Laplace ngược trên cả hai mặt.
$$ c (t) = \ left (\ frac {t ^ 2} {2} -Tt + T ^ 2-T ^ 2e ^ {- \ left (\ frac {t} {T} \ right)} \ right ) u (t) $$
Các unit parabolic response, c (t) có cả điều khoản trạng thái nhất thời và trạng thái dừng.
Số hạng nhất thời trong phản ứng parabol đơn vị là
$$ C_ {tr} (t) = - T ^ 2e ^ {- \ left (\ frac {t} {T} \ right)} u (t) $$
Thuật ngữ trạng thái ổn định trong phản ứng parabol đơn vị là
$$ C_ {ss} (t) = \ left (\ frac {t ^ 2} {2} -Tt + T ^ 2 \ right) u (t) $$
Từ những phản hồi này, chúng ta có thể kết luận rằng hệ thống điều khiển bậc nhất không ổn định với đầu vào đường dốc và parabol vì những phản hồi này tiếp tục tăng lên ngay cả trong khoảng thời gian vô hạn. Hệ thống điều khiển bậc đầu tiên ổn định với đầu vào xung và bước vì những phản hồi này có đầu ra giới hạn. Nhưng, phản ứng xung không có thời hạn trạng thái ổn định. Vì vậy, tín hiệu bước được sử dụng rộng rãi trong miền thời gian để phân tích hệ thống điều khiển từ các phản hồi của chúng.