Mô hình hóa hệ thống cơ khí
Trong chương này, chúng ta hãy thảo luận về differential equation modelingcủa hệ thống cơ khí. Có hai loại hệ thống cơ học dựa trên loại chuyển động.
- Hệ thống cơ tịnh tiến
- Hệ thống cơ quay
Mô hình hóa các hệ thống cơ tịnh tiến
Hệ thống cơ tịnh tiến chuyển động dọc theo một straight line. Các hệ thống này chủ yếu bao gồm ba yếu tố cơ bản. Đó là khối lượng, lò xo và bảng điều khiển hoặc van điều tiết.
Nếu một lực tác dụng lên một hệ cơ học tịnh tiến, thì nó sẽ bị phản lại bởi các lực ngược lại do khối lượng, độ đàn hồi và ma sát của hệ. Vì lực tác dụng và lực tác dụng ngược chiều nhau nên tổng đại số của các lực tác dụng lên hệ bằng không. Bây giờ chúng ta hãy xem lực chống đối của ba yếu tố này.
Khối lượng
Khối lượng là tài sản của một cơ thể, nó lưu trữ kinetic energy. Nếu một lực tác dụng lên một vật có khối lượngM, sau đó nó bị chống lại bởi một lực đối lập do khối lượng. Lực đối nghịch này tỷ lệ với gia tốc của cơ thể. Cho rằng lực đàn hồi và ma sát là không đáng kể.

$$ F_m \ propto \: a $$
$$ \ Rightarrow F_m = Ma = M \ frac {\ text {d} ^ 2x} {\ text {d} t ^ 2} $$
$$ F = F_m = M \ frac {\ text {d} ^ 2x} {\ text {d} t ^ 2} $$
Ở đâu,
F là lực tác dụng
Fm là lực đối lập do khối lượng
M là khối lượng
a đang tăng tốc
x là sự dịch chuyển
Mùa xuân
Spring là một phần tử, lưu trữ potential energy. Nếu một lực tác dụng vào lò xoKthì nó bị một lực ngược lại do lò xo đàn hồi. Lực cản này tỉ lệ với độ dịch chuyển của lò xo. Giả sử khối lượng và ma sát không đáng kể.

$$ F \ propto \: x $$
$$ \ Rightarrow F_k = Kx $$
$$ F = F_k = Kx $$
Ở đâu,
F là lực tác dụng
Fk là lực ngược lại do lò xo đàn hồi
K là mùa xuân không đổi
x là sự dịch chuyển
Dashpot
Nếu một lực được áp dụng trên dấu gạch ngang B, sau đó nó bị phản đối bởi một lực lượng đối lập do frictioncủa bảng điều khiển. Lực đối nghịch này tỷ lệ với vận tốc của cơ thể. Giả sử khối lượng và độ đàn hồi không đáng kể.

$$ F_b \ propto \: \ nu $$
$$ \ Rightarrow F_b = B \ nu = B \ frac {\ text {d} x} {\ text {d} t} $$
$$ F = F_b = B \ frac {\ text {d} x} {\ text {d} t} $$
Ở đâu,
Fb là lực đối lập do ma sát của dấu gạch ngang
B là hệ số ma sát
v là vận tốc
x là sự dịch chuyển
Mô hình hóa các hệ thống cơ quay
Hệ cơ quay chuyển động quanh một trục cố định. Các hệ thống này chủ yếu bao gồm ba yếu tố cơ bản. Những người đang cómoment of inertia, torsional spring và dashpot.
Nếu một mômen được đặt vào một hệ thống cơ học quay, thì nó sẽ bị các mômen ngược chiều do mômen quán tính, đàn hồi và ma sát của hệ. Vì momen lực tác dụng và momen xoắn ngược chiều nhau nên tổng đại số của momen lực tác dụng lên hệ bằng không. Bây giờ chúng ta hãy xem mô-men xoắn đối lập bởi ba yếu tố này riêng lẻ.
Lực quán tính
Trong hệ cơ học tịnh tiến, khối lượng tích trữ động năng. Tương tự, trong hệ thống cơ học quay, mômen quán tính lưu trữkinetic energy.
Nếu một mômen được đặt lên một vật có mômen quán tính J, thì nó bị một mômen ngược chiều do mômen quán tính gây ra. Mômen đối kháng này tỷ lệ với gia tốc góc của vật. Cho rằng lực đàn hồi và ma sát là không đáng kể.

$$ T_j \ propto \: \ alpha $$
$$ \ Rightarrow T_j = J \ alpha = J \ frac {\ text {d} ^ 2 \ theta} {\ text {d} t ^ 2} $$
$$ T = T_j = J \ frac {\ text {d} ^ 2 \ theta} {\ text {d} t ^ 2} $$
Ở đâu,
T là mô-men xoắn được áp dụng
Tj là mômen ngược chiều do mômen quán tính
J là mômen quán tính
α là gia tốc góc
θ là dịch chuyển góc
Mùa xuân xoắn
Trong hệ thống cơ học tịnh tiến, lò xo tích trữ thế năng. Tương tự, trong hệ thống cơ học quay, lò xo xoắnpotential energy.
Nếu một mômen được đặt vào lò xo xoắn K, khi đó nó bị biến đổi một mômen ngược chiều do lực đàn hồi của lò xo xoắn. Mômen đối kháng này tỷ lệ với độ dịch chuyển góc của lò xo xoắn. Cho rằng mômen quán tính và ma sát là không đáng kể.
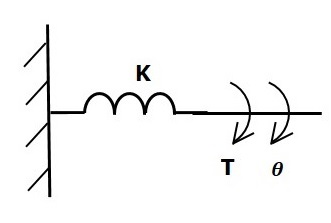
$$ T_k \ propto \: \ theta $$
$$ \ Rightarrow T_k = K \ theta $$
$$ T = T_k = K \ theta $$
Ở đâu,
T là mô-men xoắn được áp dụng
Tk là mômen ngược do đàn hồi của lò xo xoắn
K lò xo xoắn là hằng số
θ là dịch chuyển góc
Dashpot
Nếu một mô-men xoắn được áp dụng trên bảng điều khiển B, sau đó nó bị chống lại bởi một mô-men xoắn ngược lại do rotational frictioncủa bảng điều khiển. Mômen đối kháng này tỷ lệ với vận tốc góc của vật. Cho rằng momen quán tính và momen đàn hồi không đáng kể.
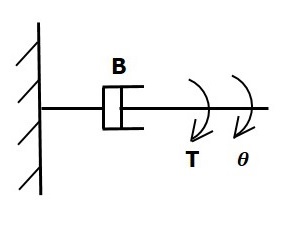
$$ T_b \ propto \: \ omega $$
$$ \ Rightarrow T_b = B \ omega = B \ frac {\ text {d} \ theta} {\ text {d} t} $$
$$ T = T_b = B \ frac {\ text {d} \ theta} {\ text {d} t} $$
Ở đâu,
Tb là mô-men xoắn ngược lại do ma sát quay của dấu gạch ngang
B là hệ số ma sát quay
ω là vận tốc góc
θ là dịch chuyển góc