Hệ thống điều khiển - Phân tích phản hồi thời gian

Chúng ta có thể phân tích đáp ứng của hệ thống điều khiển trong cả miền thời gian và miền tần số. Chúng ta sẽ thảo luận về phân tích đáp ứng tần số của hệ thống điều khiển trong các chương sau. Bây giờ chúng ta hãy thảo luận về phân tích đáp ứng thời gian của hệ thống điều khiển.

Phản hồi thời gian là gì?

Nếu đầu ra của hệ thống điều khiển cho một đầu vào thay đổi theo thời gian, thì nó được gọi là time responsecủa hệ thống điều khiển. Phản hồi thời gian bao gồm hai phần.

• Phản hồi thoáng qua
• Phản hồi trạng thái ổn định

Đáp ứng của hệ thống điều khiển trong miền thời gian được thể hiện trong hình sau.

Ở đây, cả trạng thái nhất thời và trạng thái ổn định đều được chỉ ra trong hình. Các phản hồi tương ứng với các trạng thái này được gọi là các phản ứng trạng thái tạm thời và ổn định.

Về mặt toán học, chúng ta có thể viết phản hồi thời gian c (t) là

$$ c (t) = c_ {tr} (t) + c_ {ss} (t) $$

Ở đâu,

• c _tr (t) là phản ứng nhất thời
• c _ss (t) là phản ứng ở trạng thái ổn định

Phản hồi thoáng qua

Sau khi áp dụng đầu vào vào hệ thống điều khiển, đầu ra cần một thời gian nhất định để đạt trạng thái ổn định. Vì vậy, đầu ra sẽ ở trạng thái tạm thời cho đến khi nó chuyển sang trạng thái ổn định. Do đó, phản ứng của hệ thống điều khiển trong trạng thái nhất thời được gọi làtransient response.

Phản hồi nhất thời sẽ bằng 0 đối với các giá trị lớn của 't'. Về mặt lý tưởng, giá trị này của 't' là vô cùng và trên thực tế, nó không đổi năm lần.

Về mặt toán học, chúng ta có thể viết nó là

$$ \ lim_ {t \ rightarrow \ infty} c_ {tr} (t) = 0 $$

Phản hồi ở trạng thái ổn định

Phần phản hồi thời gian vẫn còn ngay cả sau khi phản hồi nhất thời có giá trị bằng không đối với các giá trị lớn của 't' được gọi là steady state response. Điều này có nghĩa là, phản ứng nhất thời sẽ bằng 0 ngay cả trong trạng thái ổn định.

Example

Hãy để chúng tôi tìm các số hạng trạng thái nhất thời và ổn định của phản ứng thời gian của hệ thống điều khiển $ c (t) = 10 + 5e ^ {- t} $

Ở đây, số hạng thứ hai $ 5e ^ {- t} $ sẽ bằng 0 là tbiểu thị vô cùng. Vì vậy, đây làtransient term. Và số hạng đầu tiên 10 vẫn bằngttiệm cận vô cùng. Vì vậy, đây làsteady state term.

Tín hiệu kiểm tra tiêu chuẩn

Các tín hiệu kiểm tra tiêu chuẩn là xung, bước, đoạn đường nối và parabol. Các tín hiệu này được sử dụng để biết hiệu suất của hệ thống điều khiển bằng cách sử dụng đáp ứng thời gian của đầu ra.

Tín hiệu xung đơn vị

Một tín hiệu xung đơn vị, δ (t) được định nghĩa là

$ \ delta (t) = 0 $ cho $ t \ neq 0 $

và $ \ int_ {0 ^ -} ^ {0 ^ +} \ delta (t) dt = 1 $

Hình sau cho thấy tín hiệu xung đơn vị.

Vì vậy, tín hiệu xung đơn vị chỉ tồn tại tại 't' bằng không. Diện tích của tín hiệu này trong khoảng thời gian nhỏ xung quanh 't' bằng 0 là một. Giá trị của tín hiệu xung đơn vị bằng 0 đối với tất cả các giá trị khác của 't'.

Tín hiệu bước đơn vị

Một tín hiệu bước đơn vị, u (t) được định nghĩa là

$$ u (t) = 1; t \ geq 0 $$

$ = 0; t <0 $

Hình sau cho thấy tín hiệu bước đơn vị.

Vì vậy, tín hiệu bước đơn vị tồn tại cho tất cả các giá trị dương của 't' bao gồm cả 0. Và giá trị của nó là một trong khoảng thời gian này. Giá trị của tín hiệu bước đơn vị bằng 0 đối với tất cả các giá trị âm của 't'.

Tín hiệu đường dốc đơn vị

Một tín hiệu dốc đơn vị, r (t) được định nghĩa là

$$ r (t) = t; t \ geq 0 $$

$ = 0; t <0 $

Chúng ta có thể viết tín hiệu đường dốc đơn vị, $ r (t) $ theo tín hiệu bước đơn vị, $ u (t) $ dưới dạng

$$ r (t) = tu (t) $$

Hình sau cho thấy tín hiệu đường dốc đơn vị.

Vì vậy, tín hiệu dốc đơn vị tồn tại cho tất cả các giá trị dương của 't' bao gồm cả 0. Và giá trị của nó tăng tuyến tính đối với 't' trong khoảng thời gian này. Giá trị của tín hiệu đường dốc đơn vị bằng 0 đối với tất cả các giá trị âm của 't'.

Tín hiệu Parabol đơn vị

Một tín hiệu parabol đơn vị, p (t) được định nghĩa là,

$$ p (t) = \ frac {t ^ 2} {2}; t \ geq 0 $$

$ = 0; t <0 $

Chúng ta có thể viết tín hiệu parabol đơn vị, $ p (t) $ dưới dạng tín hiệu bước đơn vị, $ u (t) $ as,

$$ p (t) = \ frac {t ^ 2} {2} u (t) $$

Hình sau đây cho thấy tín hiệu parabol đơn vị.

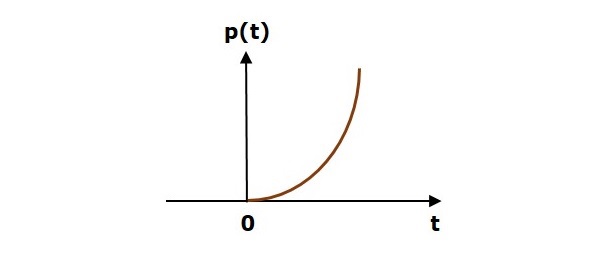
Vì vậy, tín hiệu parabol đơn vị tồn tại cho tất cả các giá trị dương của ‘t’kể cả số không. Và giá trị của nó tăng không tuyến tính đối với 't' trong khoảng thời gian này. Giá trị của tín hiệu parabol đơn vị bằng 0 đối với tất cả các giá trị âm của 't'.