Steuerungssysteme - Blockschaltbildreduzierung

Die im vorherigen Kapitel beschriebenen Konzepte sind hilfreich, um die Blockdiagramme zu reduzieren (zu vereinfachen).

Regeln zur Reduzierung von Blockdiagrammen

Befolgen Sie diese Regeln, um das Blockdiagramm mit vielen Blöcken, Summierungspunkten und Startpunkten zu vereinfachen (zu reduzieren).

Rule 1 - Auf in Reihe geschaltete Blöcke prüfen und vereinfachen.
Rule 2 - Auf parallel geschaltete Bausteine prüfen und vereinfachen.
Rule 3 - Auf die in der Rückkopplungsschleife angeschlossenen Blöcke prüfen und vereinfachen.
Rule 4 - Wenn es beim Vereinfachen Schwierigkeiten mit dem Startpunkt gibt, verschieben Sie ihn nach rechts.
Rule 5 - Wenn beim Summieren Schwierigkeiten beim Summieren auftreten, verschieben Sie ihn nach links.
Rule 6 - Wiederholen Sie die obigen Schritte, bis Sie das vereinfachte Formular erhalten, dh einen einzelnen Block.

Note - Die in diesem einzelnen Block vorhandene Übertragungsfunktion ist die Übertragungsfunktion des gesamten Blockdiagramms.

Beispiel

Betrachten Sie das in der folgenden Abbildung gezeigte Blockdiagramm. Vereinfachen (reduzieren) wir dieses Blockdiagramm mithilfe der Regeln zur Reduzierung von Blockdiagrammen.

Step 1- Verwenden Sie Regel 1 für die Blöcke $ G_1 $ und $ G_2 $. Verwenden Sie Regel 2 für die Blöcke $ G_3 $ und $ G_4 $. Das modifizierte Blockdiagramm ist in der folgenden Abbildung dargestellt.

Step 2- Verwenden Sie Regel 3 für die Blöcke $ G_1G_2 $ und $ H_1 $. Verwenden Sie Regel 4, um den Startpunkt nach dem Block $ G_5 $ zu verschieben. Das modifizierte Blockdiagramm ist in der folgenden Abbildung dargestellt.

Step 3- Verwenden Sie Regel 1 für die Blöcke $ (G_3 + G_4) $ und $ G_5 $. Das modifizierte Blockdiagramm ist in der folgenden Abbildung dargestellt.

Step 4- Verwenden Sie Regel 3 für die Blöcke $ (G_3 + G_4) G_5 $ und $ H_3 $. Das modifizierte Blockdiagramm ist in der folgenden Abbildung dargestellt.

Step 5- Verwenden Sie Regel 1 für in Reihe geschaltete Blöcke. Das modifizierte Blockdiagramm ist in der folgenden Abbildung dargestellt.

Step 6- Verwenden Sie Regel 3 für Blöcke, die in einer Rückkopplungsschleife verbunden sind. Das modifizierte Blockdiagramm ist in der folgenden Abbildung dargestellt. Dies ist das vereinfachte Blockdiagramm.

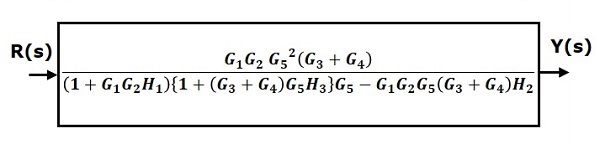
Daher ist die Übertragungsfunktion des Systems

$$ \ frac {Y (s)} {R (s)} = \ frac {G_1G_2G_5 ^ 2 (G_3 + G_4)} {(1 + G_1G_2H_1) \ lbrace 1+ (G_3 + G_4) G_5H_3 \ rbrace G_5-G_1G_2G_5 (G_3 + G_4) H_2} $$

Note - Befolgen Sie diese Schritte, um die Übertragungsfunktion des Blockdiagramms mit mehreren Eingängen zu berechnen.

Step 1 - Ermitteln Sie die Übertragungsfunktion des Blockdiagramms, indem Sie jeweils einen Eingang berücksichtigen und die verbleibenden Eingänge als Null festlegen.
Step 2 - Wiederholen Sie Schritt 1 für die verbleibenden Eingänge.
Step 3 - Holen Sie sich die gesamte Übertragungsfunktion, indem Sie alle diese Übertragungsfunktionen hinzufügen.

Der Blockdiagramm-Reduktionsprozess benötigt bei komplizierten Systemen mehr Zeit. Weil wir nach jedem Schritt das (teilweise vereinfachte) Blockdiagramm zeichnen müssen. Um diesen Nachteil zu überwinden, verwenden Sie Signalflussdiagramme (Darstellung).

In den nächsten beiden Kapiteln werden wir die Konzepte im Zusammenhang mit Signalflussgraphen diskutieren, dh wie der Signalflussgraph aus einem gegebenen Blockdiagramm dargestellt und die Übertragungsfunktion berechnet wird, indem einfach eine Verstärkungsformel verwendet wird, ohne dass ein Reduktionsprozess durchgeführt wird.