Elektrische Analogien mechanischer Systeme
Zwei Systeme sollen sein analogous miteinander, wenn die folgenden zwei Bedingungen erfüllt sind.
- Die beiden Systeme sind physikalisch unterschiedlich
- Die Differentialgleichungsmodellierung dieser beiden Systeme ist gleich
Elektrische und mechanische Systeme sind zwei physikalisch unterschiedliche Systeme. Es gibt zwei Arten elektrischer Analogien translatorischer mechanischer Systeme. Das sind Kraftspannungsanalogie und Kraftstromanalogie.
Kraftspannungsanalogie
In der Kraftspannungsanalogie sind die mathematischen Gleichungen von translational mechanical system werden mit Maschengleichungen des elektrischen Systems verglichen.
Betrachten Sie das folgende translatorische mechanische System, wie in der folgenden Abbildung gezeigt.
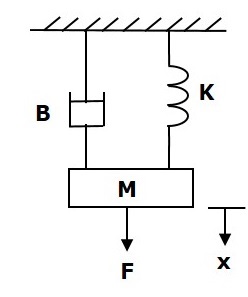
Das force balanced equation für dieses System ist
$$ F = F_m + F_b + F_k $$
$ \ Rightarrow F = M \ frac {\ text {d} ^ 2x} {\ text {d} t ^ 2} + B \ frac {\ text {d} x} {\ text {d} t} + Kx $ (Equation 1)
Betrachten Sie das folgende elektrische System wie in der folgenden Abbildung gezeigt. Diese Schaltung besteht aus einem Widerstand, einer Induktivität und einem Kondensator. Alle diese elektrischen Elemente sind in Reihe geschaltet. Die an diese Schaltung angelegte Eingangsspannung beträgt $ V $ Volt und der durch die Schaltung fließende Strom beträgt $ i $ Ampere.

Die Netzgleichung für diese Schaltung lautet
$ V = Ri + L \ frac {\ text {d} i} {\ text {d} t} + \ frac {1} {c} \ int idt $ (Equation 2)
Ersetzen Sie $ i = \ frac {\ text {d} q} {\ text {d} t} $ in Gleichung 2.
$$ V = R \ frac {\ text {d} q} {\ text {d} t} + L \ frac {\ text {d} ^ 2q} {\ text {d} t ^ 2} + \ frac { q} {C} $$
$ \ Rightarrow V = L \ frac {\ text {d} ^ 2q} {\ text {d} t ^ 2} + R \ frac {\ text {d} q} {\ text {d} t} + \ left (\ frac {1} {c} \ right) q $ (Equation 3)
Durch Vergleichen von Gleichung 1 und Gleichung 3 erhalten wir die analogen Größen des translatorischen mechanischen Systems und des elektrischen Systems. Die folgende Tabelle zeigt diese analogen Größen.
| Translationales mechanisches System | Elektrisches System |
|---|---|
| Kraft (F) | Spannung (V) |
| Masse (M) | Induktivität (L) |
| Reibungskoeffizient (B) | Widerstand (R) |
| Federkonstante (K) | Kehrwert der Kapazität $ (\ frac {1} {c}) $ |
| Verschiebung (x) | Ladung (q) |
| Geschwindigkeit (v) | Strom (i) |
In ähnlicher Weise gibt es eine Drehmomentspannungsanalogie für rotationsmechanische Systeme. Lassen Sie uns nun über diese Analogie diskutieren.
Drehmomentspannungsanalogie
In dieser Analogie sind die mathematischen Gleichungen von rotational mechanical system werden mit Maschengleichungen des elektrischen Systems verglichen.
Das rotationsmechanische System ist in der folgenden Abbildung dargestellt.

Die drehmomentausgeglichene Gleichung lautet
$$ T = T_j + T_b + T_k $$
$ \ Rightarrow T = J \ frac {\ text {d} ^ 2 \ theta} {\ text {d} t ^ 2} + B \ frac {\ text {d} \ theta} {\ text {d} t} + k \ theta $ (Equation 4)
Durch Vergleichen von Gleichung 4 und Gleichung 3 erhalten wir die analogen Größen des rotationsmechanischen Systems und des elektrischen Systems. Die folgende Tabelle zeigt diese analogen Größen.
| Rotationsmechanisches System | Elektrisches System |
|---|---|
| Drehmoment (T) | Spannung (V) |
| Trägheitsmoment (J) | Induktivität (L) |
| Rotationsreibungskoeffizient (B) | Widerstand (R) |
| Torsionsfederkonstante (K) | Kehrwert der Kapazität $ (\ frac {1} {c}) $ |
| Winkelverschiebung (θ) | Ladung (q) |
| Winkelgeschwindigkeit (ω) | Strom (i) |
Aktuelle Analogie erzwingen
In Kraftstromanalogie sind die mathematischen Gleichungen der translational mechanical system werden mit den Knotengleichungen des elektrischen Systems verglichen.
Betrachten Sie das folgende elektrische System wie in der folgenden Abbildung gezeigt. Diese Schaltung besteht aus Stromquelle, Widerstand, Induktivität und Kondensator. Alle diese elektrischen Elemente sind parallel geschaltet.

Die Knotengleichung lautet
$ i = \ frac {V} {R} + \ frac {1} {L} \ int Vdt + C \ frac {\ text {d} V} {\ text {d} t} $ (Equation 5)
Ersetzen Sie $ V = \ frac {\ text {d} \ Psi} {\ text {d} t} $ in Gleichung 5.
$$ i = \ frac {1} {R} \ frac {\ text {d} \ Psi} {\ text {d} t} + \ left (\ frac {1} {L} \ right) \ Psi + C. \ frac {\ text {d} ^ 2 \ Psi} {\ text {d} t ^ 2} $$
$ \ Rightarrow i = C \ frac {\ text {d} ^ 2 \ Psi} {\ text {d} t ^ 2} + \ left (\ frac {1} {R} \ right) \ frac {\ text { d} \ Psi} {\ text {d} t} + \ left (\ frac {1} {L} \ right) \ Psi $ (Equation 6)
Durch Vergleichen von Gleichung 1 und Gleichung 6 erhalten wir die analogen Größen des translatorischen mechanischen Systems und des elektrischen Systems. Die folgende Tabelle zeigt diese analogen Größen.
| Translationales mechanisches System | Elektrisches System |
|---|---|
| Kraft (F) | Strom (i) |
| Masse (M) | Kapazität (C) |
| Reibungskoeffizient (B) | Kehrwert des Widerstands $ (\ frac {1} {R}) $ |
| Federkonstante (K) | Kehrwert der Induktivität $ (\ frac {1} {L}) $ |
| Verschiebung (x) | Magnetfluss (ψ) |
| Geschwindigkeit (v) | Spannung (V) |
In ähnlicher Weise gibt es eine Drehmomentstromanalogie für rotationsmechanische Systeme. Lassen Sie uns nun diese Analogie diskutieren.
Drehmomentstrom-Analogie
In dieser Analogie sind die mathematischen Gleichungen der rotational mechanical system werden mit den Knotennetzgleichungen des elektrischen Systems verglichen.
Durch Vergleichen von Gleichung 4 und Gleichung 6 erhalten wir die analogen Größen des rotationsmechanischen Systems und des elektrischen Systems. Die folgende Tabelle zeigt diese analogen Größen.
| Rotationsmechanisches System | Elektrisches System |
|---|---|
| Drehmoment (T) | Strom (i) |
| Trägheitsmoment (J) | Kapazität (C) |
| Rotationsreibungskoeffizient (B) | Kehrwert des Widerstands $ (\ frac {1} {R}) $ |
| Torsionsfederkonstante (K) | Kehrwert der Induktivität $ (\ frac {1} {L}) $ |
| Winkelverschiebung (θ) | Magnetfluss (ψ) |
| Winkelgeschwindigkeit (ω) | Spannung (V) |
In diesem Kapitel haben wir die elektrischen Analogien der mechanischen Systeme diskutiert. Diese Analogien sind hilfreich, um das nichtelektrische System wie das mechanische System vom analogen elektrischen System zu untersuchen und zu analysieren.