Steuerungssysteme - Zeitverhaltensanalyse
Wir können das Verhalten der Steuerungssysteme sowohl im Zeitbereich als auch im Frequenzbereich analysieren. Wir werden die Frequenzganganalyse von Steuerungssystemen in späteren Kapiteln diskutieren. Lassen Sie uns nun über die Zeitverhaltensanalyse von Steuerungssystemen diskutieren.
Was ist Zeitantwort?
Wenn die Ausgabe des Steuersystems für eine Eingabe in Bezug auf die Zeit variiert, wird sie als bezeichnet time responsedes Steuerungssystems. Das Zeitverhalten besteht aus zwei Teilen.
- Einschwingverhalten
- Steady-State-Antwort
Die Reaktion des Steuerungssystems im Zeitbereich ist in der folgenden Abbildung dargestellt.

Hier sind in der Figur sowohl der transiente als auch der stationäre Zustand angegeben. Die diesen Zuständen entsprechenden Antworten sind als vorübergehende und stationäre Antworten bekannt.
Mathematisch können wir die Zeitantwort c (t) als schreiben
$$ c (t) = c_ {tr} (t) + c_ {ss} (t) $$
Wo,
- c tr (t) ist das Einschwingverhalten
- c ss (t) ist die stationäre Antwort
Einschwingverhalten
Nach dem Anlegen von Eingaben an das Steuerungssystem benötigt die Ausgabe eine gewisse Zeit, um den stationären Zustand zu erreichen. Der Ausgang befindet sich also im Übergangszustand, bis er in einen stabilen Zustand übergeht. Daher ist die Reaktion des Steuersystems während des Übergangszustands bekannt alstransient response.
Das Einschwingverhalten ist für große Werte von 't' Null. Idealerweise ist dieser Wert von 't' unendlich und praktisch fünfmal konstant.
Mathematisch können wir es schreiben als
$$ \ lim_ {t \ rightarrow \ infty} c_ {tr} (t) = 0 $$
Steady-State-Antwort
Der Teil der Zeitantwort, der auch nach dem Einschwingverhalten verbleibt, hat für große Werte von 't' den Wert Null steady state response. Dies bedeutet, dass das Einschwingverhalten auch im eingeschwungenen Zustand Null ist.
Example
Finden wir die transienten und stationären Terme des Zeitverhaltens des Steuerungssystems $ c (t) = 10 + 5e ^ {- t} $
Hier ist der zweite Term $ 5e ^ {- t} $ Null als tbezeichnet Unendlichkeit. Das ist also dietransient term. Und der erste Term 10 bleibt gleichtnähert sich der Unendlichkeit. Das ist also diesteady state term.
Standard-Testsignale
Die Standard-Testsignale sind Impuls, Schritt, Rampe und Parabol. Diese Signale werden verwendet, um die Leistung der Steuerungssysteme anhand des Zeitverhaltens des Ausgangs zu ermitteln.
Einheitsimpulssignal
Ein Einheitsimpulssignal δ (t) ist definiert als
$ \ delta (t) = 0 $ für $ t \ neq 0 $
und $ \ int_ {0 ^ -} ^ {0 ^ +} \ delta (t) dt = 1 $
Die folgende Abbildung zeigt das Einheitsimpulssignal.

Das Einheitsimpulssignal existiert also nur, wenn 't' gleich Null ist. Die Fläche dieses Signals unter einem kleinen Zeitintervall um 't' ist gleich Null ist Eins. Der Wert des Einheitsimpulssignals ist für alle anderen Werte von 't' Null.
Einheitsschritt-Signal
Ein Einheitsschritt-Signal u (t) ist definiert als
$$ u (t) = 1; t \ geq 0 $$
$ = 0; t <0 $
Die folgende Abbildung zeigt das Einheitsschrittsignal.

Das Einheitsschritt-Signal existiert also für alle positiven Werte von 't' einschließlich Null. Und sein Wert ist in diesem Intervall eins. Der Wert des Einheitsschrittsignals ist für alle negativen Werte von 't' Null.
Rampensignal der Einheit
Ein Einheitsrampensignal r (t) ist definiert als
$$ r (t) = t; t \ geq 0 $$
$ = 0; t <0 $
Wir können das Einheitsrampensignal $ r (t) $ als Einheitsschritt-Signal $ u (t) $ as schreiben
$$ r (t) = tu (t) $$
Die folgende Abbildung zeigt das Rampensignal der Einheit.

Das Einheitsrampensignal existiert also für alle positiven Werte von 't' einschließlich Null. Und sein Wert steigt während dieses Intervalls linear in Bezug auf 't' an. Der Wert des Einheitsrampensignals ist für alle negativen Werte von 't' Null.
Parabolisches Signal der Einheit
Ein parabolisches Einheitssignal p (t) ist definiert als:
$$ p (t) = \ frac {t ^ 2} {2}; t \ geq 0 $$
$ = 0; t <0 $
Wir können das parabolische Einheitssignal $ p (t) $ als Einheitsschritt-Signal $ u (t) $ as schreiben,
$$ p (t) = \ frac {t ^ 2} {2} u (t) $$
Die folgende Abbildung zeigt das Parabolsignal der Einheit.
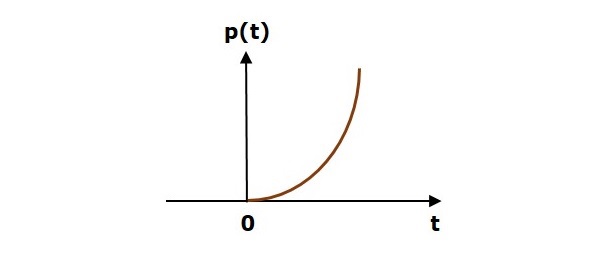
Das parabolische Einheitssignal existiert also für alle positiven Werte von ‘t’einschließlich Null. Und sein Wert steigt während dieses Intervalls nicht linear in Bezug auf 't' an. Der Wert des parabolischen Einheitssignals ist für alle negativen Werte von 't' Null.