Steuerungssysteme - Bode-Plots
Das Bode-Diagramm oder das Bode-Diagramm besteht aus zwei Diagrammen -
- Größenplot
- Phasendiagramm
In beiden Darstellungen repräsentiert die x-Achse die Winkelfrequenz (logarithmische Skala). Während die Y-Achse die Größe (lineare Skala) der Übertragungsfunktion mit offener Schleife im Betragsdiagramm und den Phasenwinkel (lineare Skala) der Übertragungsfunktion mit offener Schleife im Phasendiagramm darstellt.
Das magnitude der Übertragungsfunktion im offenen Regelkreis in dB ist -
$$ M = 20 \: \ log | G (j \ omega) H (j \ omega) | $$
Das phase angle der Übertragungsfunktion im offenen Regelkreis in Grad ist -
$$ \ phi = \ Winkel G (j \ omega) H (j \ omega) $$
Note - Die Basis des Logarithmus ist 10.
Grundlegendes zu Bode-Plots
Die folgende Tabelle zeigt die Steigungs-, Größen- und Phasenwinkelwerte der Terme, die in der Übertragungsfunktion mit offener Schleife vorhanden sind. Diese Daten sind nützlich beim Zeichnen der Bode-Diagramme.
| Art des Begriffs | G (jω) H (jω) | Steigung (dB / Dez) | Größe (dB) | Phasenwinkel (Grad) |
|---|---|---|---|---|
Konstante |
$ K $ |
$ 0 $ |
$ 20 \ log K $ |
$ 0 $ |
Null am Ursprung |
$ j \ omega $ |
$ 20 $ |
$ 20 \ log \ omega $ |
$ 90 $ |
'n' Nullen am Ursprung |
$ (j \ omega) ^ n $ |
$ 20 \: n $ |
$ 20 \: n \ log \ omega $ |
$ 90 \: n $ |
Pol am Ursprung |
$ \ frac {1} {j \ omega} $ |
$ -20 $ |
$ -20 \ log \ omega $ |
$ -90 \: oder \: 270 $ |
'n' Pole am Ursprung |
$ \ frac {1} {(j \ omega) ^ n} $ |
$ -20 \: n $ |
$ -20 \: n \ log \ omega $ |
$ -90 \: n \: oder \: 270 \: n $ |
Einfache Null |
$ 1 + j \ omega r $ |
$ 20 $ |
$ 0 \: für \: \ omega <\ frac {1} {r} $ $ 20 \: \ log \ omega r \: für \: \ omega> \ frac {1} {r} $ |
$ 0 \: für \: \ omega <\ frac {1} {r} $ $ 90 \: für \: \ omega> \ frac {1} {r} $ |
Einfache Stange |
$ \ frac {1} {1 + j \ omega r} $ |
$ -20 $ |
$ 0 \: für \: \ omega <\ frac {1} {r} $ $ -20 \: \ log \ omega r \: für \: \ omega> \ frac {1} {r} $ |
$ 0 \: für \: \ omega <\ frac {1} {r} $ $ -90 \: oder \: 270 \: für \: \ omega> \ frac {1} {r} $ |
Abgeleiteter Term zweiter Ordnung |
$ \ omega_n ^ 2 \ left (1- \ frac {\ omega ^ 2} {\ omega_n ^ 2} + \ frac {2j \ delta \ omega} {\ omega_n} \ right) $ |
$ 40 $ |
$ 40 \: \ log \: \ omega_n \: für \: \ omega <\ omega_n $ $ 20 \: \ log \ :( 2 \ delta \ omega_n ^ 2) \: für \: \ omega = \ omega_n $ $ 40 \: \ log \: \ omega \: für \: \ omega> \ omega_n $ |
$ 0 \: für \: \ omega <\ omega_n $ $ 90 \: für \: \ omega = \ omega_n $ $ 180 \: für \: \ omega> \ omega_n $ |
Integraler Term zweiter Ordnung |
$ \ frac {1} {\ omega_n ^ 2 \ left (1- \ frac {\ omega ^ 2} {\ omega_n ^ 2} + \ frac {2j \ delta \ omega} {\ omega_n} \ right)} $ |
$ -40 $ |
$ -40 \: \ log \: \ omega_n \: für \: \ omega <\ omega_n $ $ -20 \: \ log \ :( 2 \ delta \ omega_n ^ 2) \: für \: \ omega = \ omega_n $ $ -40 \: \ log \: \ omega \: für \: \ omega> \ omega_n $ |
$ -0 \: für \: \ omega <\ omega_n $ $ -90 \: für \: \ omega = \ omega_n $ $ -180 \: für \: \ omega> \ omega_n $ |
Betrachten Sie die Open-Loop-Übertragungsfunktion $ G (s) H (s) = K $.
Größe $ M = 20 \: \ log K $ dB
Phasenwinkel $ \ phi = 0 $ Grad
Wenn $ K = 1 $ ist, beträgt die Größe 0 dB.
Wenn $ K> 1 $ ist, ist die Größe positiv.
Wenn $ K <1 $ ist, ist die Größe negativ.
Die folgende Abbildung zeigt das entsprechende Bode-Diagramm.


Das Betragsdiagramm ist eine horizontale Linie, die unabhängig von der Frequenz ist. Die 0-dB-Linie selbst ist das Betragsdiagramm, wenn der Wert von K eins ist. Für die positiven Werte von K verschiebt die horizontale Linie $ 20 \: \ log K $ dB über die 0 dB-Linie. Für die negativen Werte von K verschiebt die horizontale Linie $ 20 \: \ log K $ dB unter die 0 dB-Linie. Die Null-Grad-Linie selbst ist das Phasendiagramm für alle positiven Werte von K.
Betrachten Sie die Open-Loop-Übertragungsfunktion $ G (s) H (s) = s $.
Größe $ M = 20 \ log \ omega $ dB
Phasenwinkel $ \ phi = 90 ^ 0 $
Bei $ \ omega = 0,1 $ rad / s beträgt die Größe -20 dB.
Bei $ \ omega = 1 $ rad / s beträgt die Größe 0 dB.
Bei $ \ omega = 10 $ rad / s beträgt die Größe 20 dB.
Die folgende Abbildung zeigt das entsprechende Bode-Diagramm.


Das Betragsdiagramm ist eine Linie mit einer Steigung von 20 dB / Dez. Diese Linie begann bei $ \ omega = 0,1 $ rad / s mit einer Größe von -20 dB und setzt sich auf derselben Steigung fort. Es berührt die 0-dB-Linie bei $ \ omega = 1 $ rad / sec. In diesem Fall ist das Phasendiagramm eine Linie von 90 0 .
Betrachten Sie die Open-Loop-Übertragungsfunktion $ G (s) H (s) = 1 + s \ tau $.
Größe $ M = 20 \: log \ sqrt {1 + \ omega ^ 2 \ tau ^ 2} $ dB
Phasenwinkel $ \ phi = \ tan ^ {- 1} \ omega \ tau $ Grad
Für $ ω <\ frac {1} {\ tau} $ beträgt die Größe 0 dB und der Phasenwinkel 0 Grad.
Für $ \ omega> \ frac {1} {\ tau} $ beträgt die Größe $ 20 \: \ log \ omega \ tau $ dB und der Phasenwinkel 90 0 .
Die folgende Abbildung zeigt das entsprechende Bode-Diagramm.

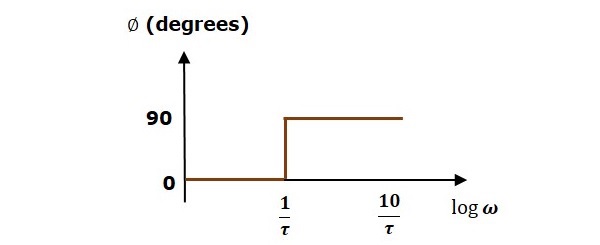
Das Betragsdiagramm hat eine Größe von 0 dB bis zu $ \ omega = \ frac {1} {\ tau} $ rad / sec. Ab $ \ omega = \ frac {1} {\ tau} $ rad / sec hat es eine Steigung von 20 dB / dec. In diesem Fall hat das Phasendiagramm einen Phasenwinkel von 0 Grad bis zu $ \ omega = \ frac {1} {\ tau} $ rad / s und von hier aus einen Phasenwinkel von 90 0 . Diese Bode-Handlung heißtasymptotic Bode plot.
Da die Größen- und Phasendiagramme mit geraden Linien dargestellt werden, ähneln die Exact Bode-Diagramme den asymptotischen Bode-Diagrammen. Der einzige Unterschied besteht darin, dass die Exact Bode-Diagramme einfache Kurven anstelle von geraden Linien aufweisen.
In ähnlicher Weise können Sie die Bode-Diagramme für andere Begriffe der Übertragungsfunktion mit offenem Regelkreis zeichnen, die in der Tabelle angegeben sind.