Konvexe Optimierung - Kurzanleitung

Dieser Kurs ist nützlich für Studenten, die nichtlineare Optimierungsprobleme lösen möchten, die in verschiedenen technischen und wissenschaftlichen Anwendungen auftreten. Dieser Kurs beginnt mit der grundlegenden Theorie der linearen Programmierung und führt in die Konzepte konvexer Mengen und Funktionen sowie in verwandte Terminologien ein, um verschiedene Theoreme zu erklären, die zur Lösung der nichtlinearen Programmierprobleme erforderlich sind. In diesem Kurs werden verschiedene Algorithmen vorgestellt, mit denen solche Probleme gelöst werden. Diese Art von Problemen tritt in verschiedenen Anwendungen auf, einschließlich maschinellem Lernen, Optimierungsproblemen in der Elektrotechnik usw. Die Schüler müssen über Vorkenntnisse in Mathematikkonzepten und -berechnungen der High School verfügen.

In diesem Kurs lernen die Schüler, die Optimierungsprobleme wie $ min f \ left (x \ right) $ unter bestimmten Einschränkungen zu lösen.

Diese Probleme sind leicht lösbar, wenn die Funktion $ f \ left (x \ right) $ eine lineare Funktion ist und wenn die Einschränkungen linear sind. Dann spricht man von einem linearen Programmierproblem (LPP). Wenn die Einschränkungen jedoch nicht linear sind, ist es schwierig, das obige Problem zu lösen. Wenn wir die Funktionen nicht in einem Diagramm darstellen können, kann der Versuch, die Optimierung zu analysieren, eine Möglichkeit sein, aber wir können eine Funktion nicht darstellen, wenn sie über drei Dimensionen hinausgeht. Daher gibt es die Techniken der nichtlinearen Programmierung oder der konvexen Programmierung, um solche Probleme zu lösen. In diesem Tutorial konzentrieren wir uns auf das Erlernen solcher Techniken und am Ende auf einige Algorithmen zur Lösung solcher Probleme. Zuerst werden wir den Begriff der konvexen Mengen bringen, der die Grundlage der konvexen Programmierprobleme bildet. Mit der Einführung konvexer Funktionen werden wir dann einige wichtige Theoreme zur Lösung dieser Probleme und einige auf diesen Theoremen basierende Algorithmen.

Terminologien

• Der Raum $ \ mathbb {R} ^ n $ - Es ist ein n-dimensionaler Vektor mit reellen Zahlen, definiert wie folgt - $ \ mathbb {R} ^ n = \ left \ {\ left (x_1, x_2, ... , x_n \ right) ^ {\ tau}: x_1, x_2, ...., x_n \ in \ mathbb {R} \ right \} $

• Der Raum $ \ mathbb {R} ^ {mXn} $ - Dies ist eine Menge aller reellen Wertematrizen der Ordnung $ mXn $.

Methodik

Die lineare Programmierung, auch lineare Optimierung genannt, ist eine Technik, mit der mathematische Probleme gelöst werden, bei denen die Beziehungen linearer Natur sind. Die grundlegende Natur der linearen Programmierung besteht darin, eine zu maximieren oder zu minimierenobjective function mit vorbehaltlich einiger constraints. Die Zielfunktion ist eine lineare Funktion, die aus dem mathematischen Modell des Problems erhalten wird. Die Einschränkungen sind die Bedingungen, die dem Modell auferlegt werden und auch linear sind.

• Finden Sie aus der gegebenen Frage die Zielfunktion.
• Finde die Einschränkungen.
• Zeichnen Sie die Einschränkungen in ein Diagramm.
• Finden Sie den realisierbaren Bereich, der durch den Schnittpunkt aller Einschränkungen gebildet wird.
• Finden Sie die Eckpunkte der möglichen Region.
• Finden Sie den Wert der Zielfunktion an diesen Eckpunkten.
• Der Eckpunkt, der die Zielfunktion (entsprechend der Frage) entweder maximiert oder minimiert, ist die Antwort.

Beispiele

Step 1 - Maximieren Sie $ 5x + 3y $ vorbehaltlich

$ x + y \ leq 2 $,

$ 3x + y \ leq 3 $,

$ x \ geq 0 \: und \: y \ geq 0 $

Solution - -

Der erste Schritt besteht darin, den möglichen Bereich in einem Diagramm zu finden.

Aus dem Diagramm geht klar hervor, dass die Eckpunkte des realisierbaren Bereichs sind

$ \ left (0, 0 \ right) \ left (0, 2 \ right) \ left (1, 0 \ right) \ left (\ frac {1} {2}, \ frac {3} {2} \ right ) $

Sei $ f \ left (x, y \ right) = 5x + 3y $

Wenn wir diese Werte in die Zielfunktion einfügen, erhalten wir -

$ f \ left (0, 0 \ right) $ = 0

$ f \ left (0, 2 \ right) $ = 6

$ f \ left (1, 0 \ right) $ = 5

$ f \ left (\ frac {1} {2}, \ frac {3} {2} \ right) $ = 7

Daher maximiert die Funktion bei $ \ left (\ frac {1} {2}, \ frac {3} {2} \ right) $

Step 2- Eine Uhrenfirma stellt eine digitale und eine mechanische Uhr her. Langzeitprojektionen deuten auf einen erwarteten Bedarf von mindestens 100 digitalen und 80 mechanischen Uhren pro Tag hin. Aufgrund der begrenzten Produktionskapazität können täglich nicht mehr als 200 digitale und 170 mechanische Uhren hergestellt werden. Um einen Versandvertrag zu erfüllen, werden täglich mindestens 200 Uhren verschickt.

Wenn jede verkaufte Digitaluhr zu einem Verlust von 2 $ führt, aber jede mechanische Uhr einen Gewinn von 5 $ erzielt, wie viele von jedem Typ sollten täglich hergestellt werden, um den Nettogewinn zu maximieren?

Solution - -

$ X $ sei die Anzahl der produzierten Digitaluhren

$ y $ ist die Anzahl der produzierten mechanischen Uhren

Entsprechend der Frage sollen täglich mindestens 100 Digitaluhren hergestellt werden und es können maximal 200 Digitaluhren hergestellt werden.

$ \ Rightarrow 100 \ leq \: x \ leq 200 $

Ebenso sollen täglich mindestens 80 mechanische Uhren hergestellt werden und maximal 170 mechanische Uhren können hergestellt werden.

$ \ Rightarrow 80 \ leq \: y \ leq 170 $

Da sollen täglich mindestens 200 Uhren produziert werden.

$ \ Rightarrow x + y \ leq 200 $

Da jede verkaufte Digitaluhr zu einem Verlust von 2 $ führt, aber jede mechanische Uhr einen Gewinn von 5 $ erzielt,

Der Gesamtgewinn kann berechnet werden als

$ Profit = -2x + 5y $

Und wir müssen den Gewinn maximieren. Daher kann die Frage wie folgt formuliert werden:

Maximieren Sie $ -2x + 5y $ vorbehaltlich

$ 100 \: \ leq x \: \ leq 200 $

$ 80 \: \ leq y \: \ leq 170 $

$ x + y \: \ leq 200 $

Wenn wir die obigen Gleichungen in einem Diagramm darstellen, erhalten wir:

Die Eckpunkte der realisierbaren Region sind

$ \ left (100, 170 \ right) \ left (200, 170 \ right) \ left (200, 180 \ right) \ left (120, 80 \ right) und \ left (100, 100 \ right) $

Der Maximalwert der Zielfunktion wird bei $ \ left (100, 170 \ right) $ erhalten. Um den Nettogewinn zu maximieren, sollten 100 Einheiten Digitaluhren und 170 Einheiten mechanische Uhren hergestellt werden.

Eine Norm ist eine Funktion, die einem Vektor oder einer Variablen einen streng positiven Wert gibt.

Norm ist eine Funktion $ f: \ mathbb {R} ^ n \ rightarrow \ mathbb {R} $

Die grundlegenden Merkmale einer Norm sind -

Sei $ X $ ein Vektor, so dass $ X \ in \ mathbb {R} ^ n $

• $ \ left \ | x \ right \ | \ geq 0 $

• $ \ left \ | x \ right \ | = 0 \ Leftrightarrow x = 0 \ forall x \ in X $

• $ \ left \ | \ alpha x \ right \ | = \ left | \ alpha \ right | \ left \ | x \ right \ | \ forall \: x \ in X und \: \ alpha \: ist \: a \: scalar $

• $ \ left \ | x + y \ right \ | \ leq \ left \ | x \ rechts \ | + \ links \ | y \ right \ | \ forall x, y \ in X $

• $ \ left \ | xy \ right \ | \ geq \ left \ | \ left \ | x \ rechts \ | - \ links \ | y \ right \ | \ right \ | $

Per Definition wird die Norm wie folgt berechnet:

• $ \ left \ | x \ rechts \ | _1 = \ Anzeigestil \ Summe \ Grenzen_ {i = 1} ^ n \ links | x_i \ right | $

• $ \ left \ | x \ rechts \ | _2 = \ links (\ Anzeigestil \ Summe \ Grenzen_ {i = 1} ^ n \ links | x_i \ rechts | ^ 2 \ rechts) ^ {\ frac {1} {2}} $

• $ \ left \ | x \ rechts \ | _p = \ links (\ Anzeigestil \ Summe \ Grenzen_ {i = 1} ^ n \ links | x_i \ rechts | ^ p \ rechts) ^ {\ frac {1} {p}}, 1 \ leq p \ leq \ infty $

Norm ist eine stetige Funktion.

Beweis

Per Definition ist $ f \ left (x \ right) $ eine konstante Funktion, wenn $ x_n \ rightarrow x $ in $ X \ Rightarrow f \ left (x_n \ right) \ rightarrow f \ left (x \ right) $ ist.

Sei $ f \ left (x \ right) = \ left \ | x \ right \ | $

Daher ist $ \ left | f \ left (x_n \ right) -f \ left (x \ right) \ right | = \ left | \ left \ | x_n \ right \ | - \ left \ | x \ right \ | \ right | \ leq \ left | \ left | x_n-x \ right | \: \ right | $

Da $ x_n \ rightarrow x $ also $ \ left \ | ist x_n-x \ right \ | \ rightarrow 0 $

Deshalb $ \ left | f \ left (x_n \ right) -f \ left (x \ right) \ right | \ leq 0 \ Rightarrow \ left | f \ left (x_n \ right) -f \ left (x \ right) \ right | = 0 \ Rightarrow f \ left (x_n \ right) \ rightarrow f \ left (x \ right) $

Norm ist also eine stetige Funktion.

Das innere Produkt ist eine Funktion, die einem Vektorpaar einen Skalar gibt.

Inneres Produkt - $ f: \ mathbb {R} ^ n \ times \ mathbb {R} ^ n \ rightarrow \ kappa $ wobei $ \ kappa $ ein Skalar ist.

Die grundlegenden Eigenschaften des inneren Produkts sind wie folgt:

Lassen Sie $ X \ in \ mathbb {R} ^ n $

• $ \ left \ langle x, x \ right \ rangle \ geq 0, \ forall x \ in X $

• $ \ left \ langle x, x \ right \ rangle = 0 \ Leftrightarrow x = 0, \ forall x \ in X $

• $ \ left \ langle \ alpha x, y \ right \ rangle = \ alpha \ left \ langle x, y \ right \ rangle, \ forall \ alpha \ in \ kappa \: und \: \ forall x, y \ in X. $

• $ \ left \ langle x + y, z \ right \ rangle = \ left \ langle x, z \ right \ rangle + \ left \ langle y, z \ right \ rangle, \ forall x, y, z \ in X $

• $ \ left \ langle \ overline {y, x} \ right \ rangle = \ left (x, y \ right), \ forall x, y \ in X $

Note - -

• Beziehung zwischen Norm und innerem Produkt: $ \ left \ | x \ right \ | = \ sqrt {\ left (x, x \ right)} $

• $ \ forall x, y \ in \ mathbb {R} ^ n, \ left \ langle x, y \ right \ rangle = x_1y_1 + x_2y_2 + ... + x_ny_n $

Beispiele

1. Finden Sie das innere Produkt von $ x = \ left (1,2,1 \ right) \: und \: y = \ left (3, -1,3 \ right) $

Lösung

$ \ left \ langle x, y \ right \ rangle = x_1y_1 + x_2y_2 + x_3y_3 $

$ \ left \ langle x, y \ right \ rangle = \ left (1 \ times3 \ right) + \ left (2 \ times-1 \ right) + \ left (1 \ times3 \ right) $

$ \ left \ langle x, y \ right \ rangle = 3 + \ left (-2 \ right) + 3 $

$ \ left \ langle x, y \ right \ rangle = 4 $

2. Wenn $ x = \ left (4,9,1 \ right), y = \ left (-3,5,1 \ right) $ und $ z = \ left (2,4,1 \ right) $, finde $ \ left (x + y, z \ right) $

Lösung

Wie wir wissen, ist $ \ left \ langle x + y, z \ right \ rangle = \ left \ langle x, z \ right \ rangle + \ left \ langle y, z \ right \ rangle $

$ \ left \ langle x + y, z \ right \ rangle = \ left (x_1z_1 + x_2z_2 + x_3z_3 \ right) + \ left (y_1z_1 + y_2z_2 + y_3z_3 \ right) $

$ \ left \ langle x + y, z \ right \ rangle = \ left \ {\ left (4 \ times 2 \ right) + \ left (9 \ times 4 \ right) + \ left (1 \ times1 \ right) \ right \} + $

$ \ left \ {\ left (-3 \ times2 \ right) + \ left (5 \ times4 \ right) + \ left (1 \ times 1 \ right) \ right \} $

$ \ left \ langle x + y, z \ right \ rangle = \ left (8 + 36 + 1 \ right) + \ left (-6 + 20 + 1 \ right) $

$ \ left \ langle x + y, z \ right \ rangle = 45 + 15 $

$ \ left \ langle x + y, z \ right \ rangle = 60 $

Lokale Minima oder Minimieren

$ \ bar {x} \ in \: S $ wird als lokales Minimum einer Funktion $ f $ bezeichnet, wenn $ f \ left (\ bar {x} \ right) \ leq f \ left (x \ right), \ forall x \ in N_ \ varepsilon \ left (\ bar {x} \ right) $ wobei $ N_ \ varepsilon \ left (\ bar {x} \ right) $ die Nachbarschaft von $ \ bar {x} $ bedeutet, dh $ N_ \ varepsilon \ left (\ bar {x} \ right) $ bedeutet $ \ left \ | x- \ bar {x} \ right \ | <\ varepsilon $

Lokale Maxima oder Maximizer

$ \ bar {x} \ in \: S $ wird als lokales Maximum einer Funktion $ f $ bezeichnet, wenn $ f \ left (\ bar {x} \ right) \ geq f \ left (x \ right), \ forall x \ in N_ \ varepsilon \ left (\ bar {x} \ right) $ wobei $ N_ \ varepsilon \ left (\ bar {x} \ right) $ die Nachbarschaft von $ \ bar {x} $ bedeutet, dh $ N_ \ varepsilon \ left (\ bar {x} \ right) $ bedeutet $ \ left \ | x- \ bar {x} \ right \ | <\ varepsilon $

Globale Minima

$ \ bar {x} \ in \: S $ wird als globales Minimum einer Funktion $ f $ bezeichnet, wenn $ f \ left (\ bar {x} \ right) \ leq f \ left (x \ right), \ für alle x \ in S $

Globale Maxima

$ \ bar {x} \ in \: S $ wird als globales Maximum einer Funktion $ f $ bezeichnet, wenn $ f \ left (\ bar {x} \ right) \ geq f \ left (x \ right), \ für alle x \ in S $

Beispiele

Step 1- Finden Sie die lokalen Minima und Maxima von $ f \ left (\ bar {x} \ right) = \ left | x ^ 2-4 \ right | $

Solution - -

Aus dem Diagramm der obigen Funktion ist ersichtlich, dass die lokalen Minima bei $ x = \ pm 2 $ und die lokalen Maxima bei $ x = 0 $ auftreten

Step 2- Finden Sie die globalen Minima der Funktion $ f \ left (x \ right) = \ left | 4x ^ 3-3x ^ 2 + 7 \ right | $

Solution - -

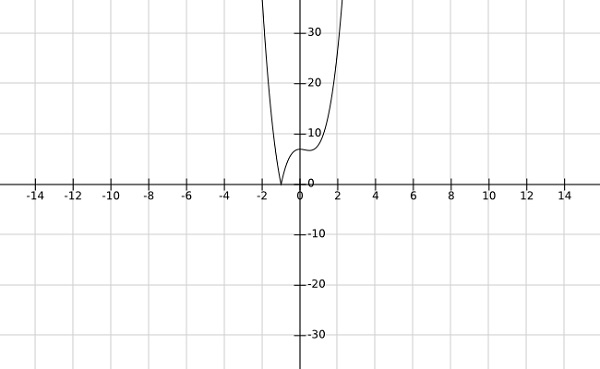
Aus dem Diagramm der obigen Funktion geht hervor, dass die globalen Minima bei $ x = -1 $ auftreten.

Sei $ S \ subseteq \ mathbb {R} ^ n $ Eine Menge S wird als konvex bezeichnet, wenn das Liniensegment, das zwei beliebige Punkte der Menge S verbindet, auch zu S gehört, dh wenn $ x_1, x_2 \ in S $ , dann $ \ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ in S $ wobei $ \ lambda \ in \ left (0,1 \ right) $.

Note - -

• Die Vereinigung zweier konvexer Mengen kann konvex sein oder nicht.
• Der Schnittpunkt zweier konvexer Mengen ist immer konvex.

Proof

Sei $ S_1 $ und $ S_2 $ zwei konvexe Mengen.

Sei $ S_3 = S_1 \ cap S_2 $

Sei $ x_1, x_2 \ in S_3 $

Da $ S_3 = S_1 \ cap S_2 $ also $ x_1, x_2 \ in S_1 $ und $ x_1, x_2 \ in S_2 $

Da $ S_i $ konvex gesetzt ist, ist $ \ forall $ $ i \ in 1,2, $

Also $ \ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ in S_i $ wobei $ \ lambda \ in \ left (0,1 \ right) $

Daher $ \ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ in S_1 \ cap S_2 $

$ \ Rightarrow \ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ in S_3 $

Daher ist $ S_3 $ eine konvexe Menge.

• Gewichteter Durchschnitt der Form $ \ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_ix_i $, wobei $ \ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_i = 1 $ und $ \ lambda_i \ geq 0 , \ forall i \ in \ left [1, k \ right] $ heißt konische Kombination von $ x_1, x_2, .... x_k. $

• Der gewichtete Durchschnitt der Form $ \ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_ix_i $, wobei $ \ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_i = 1 $ als affine Kombination von $ x_1 bezeichnet wird , x_2, .... x_k. $

• Der gewichtete Durchschnitt der Form $ \ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_ix_i $ heißt lineare Kombination von $ x_1, x_2, .... x_k. $

Beispiele

Step 1 - Beweisen Sie, dass die Menge $ S = \ left \ {x \ in \ mathbb {R} ^ n: Cx \ leq \ alpha \ right \} $ eine konvexe Menge ist.

Lösung

Sei $ x_1 $ und $ x_2 \ in S $

$ \ Rightarrow Cx_1 \ leq \ alpha $ und $ \: und \: Cx_2 \ leq \ alpha $

Zum Anzeigen: $ \: \: y = \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ in S \: \ forall \: \ lambda \ in \ left (0,1 \ rechts) $

$ Cy = C \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) = \ lambda Cx_1 + \ left (1- \ lambda \ right) Cx_2 $

$ \ Rightarrow Cy \ leq \ lambda \ alpha + \ left (1- \ lambda \ right) \ alpha $

$ \ Rightarrow Cy \ leq \ alpha $

$ \ Rightarrow y \ in S $

Daher ist $ S $ eine konvexe Menge.

Step 2 - Beweisen Sie, dass die Menge $ S = \ left \ {\ left (x_1, x_2 \ right) \ in \ mathbb {R} ^ 2: x_ {1} ^ {2} \ leq 8x_2 \ right \} $ konvex ist einstellen.

Lösung

Sei $ x, y \ in S $

Sei $ x = \ left (x_1, x_2 \ right) $ und $ y = \ left (y_1, y_2 \ right) $

$ \ Rightarrow x_ {1} ^ {2} \ leq 8x_2 $ und $ y_ {1} ^ {2} \ leq 8y_2 $

Um zu zeigen - $ \ lambda x + \ left (1- \ lambda \ right) y \ in S \ Rightarrow \ lambda \ left (x_1, x_2 \ right) + \ left (1- \ lambda \ right) \ left (y_1, y_2 \ rechts) \ in S \ Rechtspfeil \ links [\ lambda x_1 + \ links (1- \ lambda) y_2] \ in S \ rechts) \ rechts] $

$ Nun, \ left [\ lambda x_1 + \ left (1- \ lambda \ right) y_1 \ right] ^ {2} = \ lambda ^ 2x_ {1} ^ {2} + \ left (1- \ lambda \ right) ^ 2y_ {1} ^ {2} +2 \ lambda \ left (1- \ lambda \ right) x_1y_1 $

Aber $ 2x_1y_1 \ leq x_ {1} ^ {2} + y_ {1} ^ {2} $

Deshalb,

$ \ left [\ lambda x_1 + \ left (1- \ lambda \ right) y_1 \ right] ^ {2} \ leq \ lambda ^ 2x_ {1} ^ {2} + \ left (1- \ lambda \ right) ^ 2y_ {1} ^ {2} +2 \ lambda \ left (1- \ lambda \ right) \ left (x_ {1} ^ {2} + y_ {1} ^ {2} \ right) $

$ \ Rightarrow \ left [\ lambda x_1 + \ left (1- \ lambda \ right) y_1 \ right] ^ {2} \ leq \ lambda x_ {1} ^ {2} + \ left (1- \ lambda \ right) y_ {1} ^ {2} $

$ \ Rightarrow \ left [\ lambda x_1 + \ left (1- \ lambda \ right) y_1 \ right] ^ {2} \ leq 8 \ lambda x_2 + 8 \ left (1- \ lambda \ right) y_2 $

$ \ Rightarrow \ left [\ lambda x_1 + \ left (1- \ lambda \ right) y_1 \ right] ^ {2} \ leq 8 \ left [\ lambda x_2 + \ left (1- \ lambda \ right) y_2 \ right] $

$ \ Rightarrow \ lambda x + \ left (1- \ lambda \ right) y \ in S $

Step 3 - Zeigen Sie, dass eine Menge $ S \ in \ mathbb {R} ^ n $ genau dann konvex ist, wenn für jede ganze Zahl k jede konvexe Kombination von k Punkten von $ S $ in $ S $ ist.

Lösung

Sei $ S $ eine konvexe Menge. dann zu zeigen;

$ c_1x_1 + c_2x_2 + ..... + c_kx_k \ in S, \ Anzeigestil \ Summe \ Grenzen_ {1} ^ k c_i = 1, c_i \ geq 0, \ forall i \ in 1,2, ...., k $

Beweis durch Induktion

Für $ k = 1 ist x_1 \ in S, c_1 = 1 \ Rightarrow c_1x_1 \ in S $

Für $ k = 2 ist x_1, x_2 \ in S c_1 + c_2 = 1 $ und Da S eine konvexe Menge ist

$ \ Rightarrow c_1x_1 + c_2x_2 \ in S. $

Die konvexe Kombination von m Punkten von S sei in S, dh

$ c_1x_1 + c_2x_2 + ... + c_mx_m \ in S, \ Anzeigestil \ Summe \ Grenzen_ {1} ^ m c_i = 1, c_i \ geq 0, \ forall i \ in 1,2, ..., m $

Nun sei $ x_1, x_2 ...., x_m, x_ {m + 1} \ in S $

Sei $ x = \ mu_1x_1 + \ mu_2x_2 + ... + \ mu_mx_m + \ mu_ {m + 1} x_ {m + 1} $

Sei $ x = \ left (\ mu_1 + \ mu_2 + ... + \ mu_m \ right) \ frac {\ mu_1x_1 + \ mu_2x_2 + \ mu_mx_m} {\ mu_1 + \ mu_2 + ......... + \ mu_m} + \ mu_ {m + 1} x_ {m + 1} $

Sei $ y = \ frac {\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_mx_m} {\ mu_1 + \ mu_2 + ......... + \ mu_m} $

$ \ Rightarrow x = \ left (\ mu_1 + \ mu_2 + ... + \ mu_m \ right) y + \ mu_ {m + 1} x_ {m + 1} $

Jetzt $ y \ in S $, weil die Summe der Koeffizienten 1 ist.

$ \ Rightarrow x \ in S $, da S eine konvexe Menge ist und $ y, x_ {m + 1} \ in S $

Daher durch Induktion bewiesen.

Eine Menge $ A $ wird als affine Menge bezeichnet, wenn für zwei verschiedene Punkte die Linie, die durch diese Punkte verläuft, in der Menge $ A $ liegt.

Note - -

• $ S $ ist genau dann eine affine Menge, wenn sie jede affine Kombination ihrer Punkte enthält.

• Leere und Singleton-Mengen sind sowohl affine als auch konvexe Mengen.

  Zum Beispiel ist die Lösung einer linearen Gleichung eine affine Menge.

Beweis

Sei S die Lösung einer linearen Gleichung.

Per Definition ist $ S = \ left \ {x \ in \ mathbb {R} ^ n: Ax = b \ right \} $

Sei $ x_1, x_2 \ in S \ Rightarrow Ax_1 = b $ und $ Ax_2 = b $

Um zu beweisen: $ A \ left [\ theta x_1 + \ left (1- \ theta \ right) x_2 \ right] = b, \ forall \ theta \ in \ left (0,1 \ right) $

$ A \ left [\ theta x_1 + \ left (1- \ theta \ right) x_2 \ right] = \ theta Ax_1 + \ left (1- \ theta \ right) Ax_2 = \ theta b + \ left (1- \ theta \ right) ) b = b $

Somit ist S eine affine Menge.

Satz

Wenn $ C $ eine affine Menge ist und $ x_0 \ in C $, dann ist die Menge $ V = C-x_0 = \ left \ {x-x_0: x \ in C \ right \} $ ein Unterraum von C.

Beweis

Sei $ x_1, x_2 \ in V $

Zum Anzeigen: $ \ alpha x_1 + \ beta x_2 \ in V $ für einige $ \ alpha, \ beta $

Nun $ x_1 + x_0 \ in C $ und $ x_2 + x_0 \ in C $ per Definition von V.

Nun ist $ \ alpha x_1 + \ beta x_2 + x_0 = \ alpha \ left (x_1 + x_0 \ right) + \ beta \ left (x_2 + x_0 \ right) + \ left (1- \ alpha - \ beta \ right) x_0 $

Aber $ \ alpha \ left (x_1 + x_0 \ right) + \ beta \ left (x_2 + x_0 \ right) + \ left (1- \ alpha - \ beta \ right) x_0 \ in C $, weil C eine affine Menge ist .

Daher $ \ alpha x_1 + \ beta x_2 \ in V $

Daher bewiesen.

Die konvexe Hülle einer Menge von Punkten in S ist die Grenze des kleinsten konvexen Bereichs, der alle Punkte von S in sich oder an seiner Grenze enthält.

ODER

Sei $ S \ subseteq \ mathbb {R} ^ n $ Die konvexe Hülle von S, die mit $ Co \ left (S \ right) $ bezeichnet wird, ist die Sammlung aller konvexen Kombinationen von S, dh $ x \ in Co \ left (S \ rechts) $ genau dann, wenn $ x \ in \ Anzeigestil \ Summe \ Grenzen_ {i = 1} ^ n \ lambda_ix_i $, wobei $ \ Anzeigestil \ Summe \ Grenzen_ {1} ^ n \ lambda_i = 1 $ und $ \ lambda_i \ geq 0 \ forall x_i \ in S $

Remark - Der Konve-Rumpf einer Menge von Punkten in S in der Ebene definiert ein konvexes Polygon und die Punkte von S an der Grenze des Polygons definieren die Eckpunkte des Polygons.

Theorem $ Co \ left (S \ right) = \ left \ {x: x = \ displaystyle \ sum \ limit_ {i = 1} ^ n \ lambda_ix_i, x_i \ in S, \ displaystyle \ sum \ limit_ {i = 1} ^ n \ lambda_i = 1, \ lambda_i \ geq 0 \ right \} $ Zeigen Sie, dass eine konvexe Hülle eine konvexe Menge ist.

Beweis

Sei $ x_1, x_2 \ in Co \ left (S \ right) $, dann $ x_1 = \ displaystyle \ sum \ limit_ {i = 1} ^ n \ lambda_ix_i $ und $ x_2 = \ displaystyle \ sum \ limit_ {i = 1} ^ n \ lambda_ \ gamma x_i $ wobei $ \ displaystyle \ sum \ limit_ {i = 1} ^ n \ lambda_i = 1, \ lambda_i \ geq 0 $ und $ \ displaystyle \ sum \ limit_ {i = 1} ^ n \ gamma_i = 1, \ gamma_i \ geq0 $

Für $ \ theta \ in \ left (0,1 \ right), \ theta x_1 + \ left (1- \ theta \ right) x_2 = \ theta \ displaystyle \ sum \ limit_ {i = 1} ^ n \ lambda_ix_i + \ left (1- \ theta \ right) \ displaystyle \ sum \ limit_ {i = 1} ^ n \ gamma_ix_i $

$ \ theta x_1 + \ left (1- \ theta \ right) x_2 = \ Anzeigestil \ Summe \ Grenzen_ {i = 1} ^ n \ Lambda_i \ Theta x_i + \ Anzeigestil \ Summe \ Grenzen_ {i = 1} ^ n \ gamma_i \ links (1- \ Theta \ rechts) x_i $

$ \ theta x_1 + \ left (1- \ theta \ right) x_2 = \ displaystyle \ sum \ border_ {i = 1} ^ n \ left [\ lambda_i \ theta + \ gamma_i \ left (1- \ theta \ right) \ rechts] x_i $

Unter Berücksichtigung der Koeffizienten,

$ \ displaystyle \ sum \ limit_ {i = 1} ^ n \ left [\ lambda_i \ theta + \ gamma_i \ left (1- \ theta \ right) \ right] = \ theta \ displaystyle \ sum \ border_ {i = 1 } ^ n \ lambda_i + \ left (1- \ theta \ right) \ displaystyle \ sum \ border_ {i = 1} ^ n \ gamma_i = \ theta + \ left (1- \ theta \ right) = 1 $

Daher ist $ \ theta x_1 + \ left (1- \ theta \ right) x_2 \ in Co \ left (S \ right) $

Somit ist eine konvexe Hülle eine konvexe Menge.

Sei S eine beliebige Menge in $ \ mathbb {R} ^ n $. Wenn $ x \ in Co \ left (S \ right) $, dann $ x \ in Co \ left (x_1, x_2, ...., x_n, x_ {n + 1} \ right) $.

Beweis

Da $ x \ in Co \ left (S \ right) $ ist, wird $ x $ durch eine konvexe Kombination einer endlichen Anzahl von Punkten in S dargestellt, dh

$ x = \ Anzeigestil \ Summe \ Grenzen_ {j = 1} ^ k \ lambda_jx_j, \ Anzeigestil \ Summe \ Grenzen_ {j = 1} ^ k \ lambda_j = 1, \ lambda_j \ geq 0 $ und $ x_j \ in S, \ forall j \ in \ left (1, k \ right) $

Wenn $ k \ leq n + 1 $ ist, ist das erhaltene Ergebnis offensichtlich wahr.

Wenn $ k \ geq n + 1 $, dann sind $ \ left (x_2-x_1 \ right) \ left (x_3-x_1 \ right), ....., \ left (x_k-x_1 \ right) $ linear abhängig .

$ \ Rightarrow \ existiert \ mu _j \ in \ mathbb {R}, 2 \ leq j \ leq k $ (nicht alle Null), so dass $ \ displaystyle \ sum \ limit_ {j = 2} ^ k \ mu _j \ left (x_j-x_1 \ right) = 0 $

Definieren Sie $ \ mu_1 = - \ Anzeigestil \ Summe \ Grenzen_ {j = 2} ^ k \ mu _j $, dann $ \ Anzeigestil \ Summe \ Grenzen_ {j = 1} ^ k \ mu_j x_j = 0, \ Anzeigestil \ Summe \ Grenzen_ {j = 1} ^ k \ mu_j = 0 $

wobei nicht alle $ \ mu_js $ gleich Null sind. Da $ \ displaystyle \ sum \ limit_ {j = 1} ^ k \ mu_j = 0 $ ist, muss mindestens eines der $ \ mu_j> 0,1 \ leq j \ leq k $

Dann ist $ x = \ displaystyle \ sum \ limit_ {1} ^ k \ lambda_j x_j + 0 $

$ x = \ displaystyle \ sum \ limit_ {1} ^ k \ lambda_j x_j- \ alpha \ displaystyle \ sum \ limit_ {1} ^ k \ mu_j x_j $

$ x = \ displaystyle \ sum \ limit_ {1} ^ k \ left (\ lambda_j- \ alpha \ mu_j \ right) x_j $

Wählen Sie $ \ alpha $ so, dass $ \ alpha = min \ left \ {\ frac {\ lambda_j} {\ mu_j}, \ mu_j \ geq 0 \ right \} = \ frac {\ lambda_j} {\ mu _j}, $ für einige $ i = 1,2, ..., k $

Wenn $ \ mu_j \ leq 0, \ lambda_j- \ alpha \ mu_j \ geq 0 $

Wenn $ \ mu_j> 0, dann \: \ frac {\ lambda _j} {\ mu_j} \ geq \ frac {\ lambda_i} {\ mu _i} = \ alpha \ Rightarrow \ lambda_j- \ alpha \ mu_j \ geq 0, j = 1,2, ... k $

Insbesondere ist $ \ lambda_i- \ alpha \ mu_i = 0 $, per Definition von $ \ alpha $

$ x = \ displaystyle \ sum \ limit_ {j = 1} ^ k \ left (\ lambda_j- \ alpha \ mu_j \ right) x_j $, wobei

$ \ lambda_j- \ alpha \ mu_j \ geq0 $ und $ \ displaystyle \ sum \ limit_ {j = 1} ^ k \ left (\ lambda_j- \ alpha \ mu_j \ right) = 1 $ und $ \ lambda_i- \ alpha \ mu_i = 0 $

Somit kann x als eine konvexe Kombination von höchstens (k-1) Punkten dargestellt werden.

Dieser Reduktionsprozess kann wiederholt werden, bis x als konvexe Kombination von (n + 1) Elementen dargestellt wird.

Sei S eine nicht leere, geschlossene und begrenzte Menge (auch als kompakte Menge bezeichnet) in $ \ mathbb {R} ^ n $ und sei $ f: S \ rightarrow \ mathbb {R} $ eine stetige Funktion auf S, dann die Problem min $ \ left \ {f \ left (x \ right): x \ in S \ right \} $ erreicht sein Minimum.

Beweis

Da S nicht leer und begrenzt ist, existiert eine Untergrenze.

$ \ alpha = Inf \ left \ {f \ left (x \ right): x \ in S \ right \} $

Nun sei $ S_j = \ left \ {x \ in S: \ alpha \ leq f \ left (x \ right) \ leq \ alpha + \ delta ^ j \ right \} \ forall j = 1,2, ... $ und $ \ delta \ in \ left (0,1 \ right) $

Nach der Definition von Infimium ist $ S_j $ für jedes $ j $ nicht leer.

Wählen Sie $ x_j \ in S_j $, um eine Sequenz $ \ left \ {x_j \ right \} $ für $ j = 1,2, ... $ zu erhalten

Da S begrenzt ist, ist auch die Sequenz begrenzt und es gibt eine konvergente Teilsequenz $ \ left \ {y_j \ right \} $, die zu $ ​​\ hat {x} $ konvergiert. Daher ist $ \ hat {x} $ ein Grenzpunkt und S ist geschlossen, daher ist $ \ hat {x} \ in S $. Da f stetig ist, ist $ f \ left (y_i \ right) \ rightarrow f \ left (\ hat {x} \ right) $.

Da $ \ alpha \ leq f \ left (y_i \ right) \ leq \ alpha + \ delta ^ k, \ alpha = \ displaystyle \ lim_ {k \ rightarrow \ infty} f \ left (y_i \ right) = f \ left ( \ hat {x} \ right) $

Somit ist $ \ hat {x} $ die Minimierungslösung.

Bemerkungen

Es gibt zwei wichtige notwendige Bedingungen, die der Weierstrass-Satz erfüllen muss. Diese sind wie folgt -

• Step 1 - Die Menge S sollte eine begrenzte Menge sein.

  Betrachten Sie die Funktion f \ left (x \ right) = x $.

  Es ist eine unbegrenzte Menge und hat an jedem Punkt in seiner Domäne ein Minimum.

  Damit Minima erhalten werden können, sollte S begrenzt sein.

• Step 2 - Das Set S sollte geschlossen sein.

  Betrachten Sie die Funktion $ f \ left (x \ right) = \ frac {1} {x} $ in der Domain \ left (0,1 \ right).

  Diese Funktion ist in der angegebenen Domäne nicht geschlossen und ihre Minima existieren ebenfalls nicht.

  Daher sollte S geschlossen sein, damit Minima erhalten werden.

Sei S eine nicht leere geschlossene konvexe Menge in $ \ mathbb {R} ^ n $ und sei $ y \ notin S $, dann existiert $ \ $ ein Punkt $ \ bar {x} \ in S $ mit minimalem Abstand von y, dh $ \ left \ | y- \ bar {x} \ right \ | \ leq \ left \ | yx \ right \ | \ forall x \ in S. $

Darüber hinaus ist $ \ bar {x} $ genau dann ein Minimierungspunkt, wenn $ \ left (y- \ hat {x} \ right) ^ {T} \ left (x- \ hat {x} \ right) \ leq 0 $ oder $ \ left (y- \ hat {x}, x- \ hat {x} \ right) \ leq 0 $

Beweis

Existenz des nächsten Punktes

Da $ S \ ne \ phi, \ existiert $ ein Punkt $ \ hat {x} \ in S $, so dass der Mindestabstand von S von y kleiner oder gleich $ \ left \ | ist y- \ hat {x} \ right \ | $.

Definieren Sie $ \ hat {S} = S \ cap \ left \ {x: \ left \ | yx \ right \ | \ leq \ left \ | y- \ hat {x} \ right \ | \ right \} $

Da $ \ hat {S} $ geschlossen und begrenzt ist und Norm eine stetige Funktion ist, existiert nach dem Weierstrass-Theorem ein Mindestpunkt $ \ hat {x} \ in S $, so dass $ \ left \ | y- \ hat {x} \ right \ | = Inf \ left \ {\ left \ | yx \ right \ |, x \ in S \ right \} $

Einzigartigkeit

Angenommen, $ \ bar {x} \ in S $, so dass $ \ left \ | y- \ hat {x} \ right \ | = \ left \ | y- \ hat {x} \ right \ | = \ alpha $

Da S konvex ist, ist $ \ frac {\ hat {x} + \ bar {x}} {2} \ in S $

Aber $ \ left \ | y- \ frac {\ hat {x} - \ bar {x}} {2} \ right \ | \ leq \ frac {1} {2} \ left \ | y- \ hat {x} \ right \ | + \ frac {1} {2} \ left \ | y- \ bar {x} \ right \ | = \ alpha $

Es kann keine strikte Ungleichung sein, da $ \ hat {x} $ y am nächsten ist.

Daher $ \ left \ | y- \ hat {x} \ right \ | = \ mu \ left \ | y- \ hat {x} \ right \ | $, für einige $ \ mu $

Jetzt $ \ left \ | \ mu \ right \ | = 1. $ Wenn $ \ mu = -1 $, dann ist $ \ left (y- \ hat {x} \ right) = - \ left (y- \ hat {x} \ right) \ Rechter Pfeil y = \ frac {\ hat {x} + \ bar {x}} {2} \ in S $

Aber $ y \ in S $. Daher Widerspruch. Also $ \ mu = 1 \ Rightarrow \ hat {x} = \ bar {x} $

Somit ist der Minimierungspunkt einzigartig.

Nehmen Sie für den zweiten Teil des Beweises $ \ left (y- \ hat {x} \ right) ^ {\ tau} \ left (x- \ bar {x} \ right) \ leq 0 $ für alle $ x \ an in S $

Jetzt,

$ \ left \ | yx \ right \ | ^ {2} = \ left \ | y- \ hat {x} + \ hat {x} -x \ right \ | ^ {2} = \ left \ | y- \ hat {x} \ right \ | ^ {2} + \ left \ | \ hat {x} -x \ right \ | ^ {2} +2 \ left (\ hat {x} -x \ right) ^ {\ tau} \ left (y- \ hat {x} \ right) $

$ \ Rightarrow \ left \ | yx \ right \ | ^ {2} \ geq \ left \ | y- \ hat {x} \ right \ | ^ {2} $ weil $ \ left \ | \ hat {x} -x \ right \ | ^ {2} \ geq 0 $ und $ \ left (\ hat {x} - x \ right) ^ {T} \ left (y- \ hat {x} \ right ) \ geq 0 $

Somit minimiert $ \ hat {x} $ den Punkt.

Nehmen Sie umgekehrt an, dass $ \ hat {x} $ ein Minimierungspunkt ist.

$ \ Rightarrow \ left \ | yx \ right \ | ^ {2} \ geq \ left \ | y- \ hat {x} \ right \ | ^ 2 \ forall x \ in S $

Da S konvex gesetzt ist.

$ \ Rightarrow \ lambda x + \ left (1- \ lambda \ right) \ hat {x} = \ hat {x} + \ lambda \ left (x- \ hat {x} \ right) \ in S $ für $ x \ in S $ und $ \ lambda \ in \ left (0,1 \ right) $

Nun $ \ left \ | y- \ hat {x} - \ lambda \ left (x- \ hat {x} \ right) \ right \ | ^ {2} \ geq \ left \ | y- \ hat {x} \ right \ | ^ 2 $

Und

$ \ left \ | y- \ hat {x} - \ lambda \ left (x- \ hat {x} \ right) \ right \ | ^ {2} = \ left \ | y- \ hat {x} \ right \ | ^ {2} + \ lambda ^ 2 \ left \ | x- \ hat {x} \ right \ | ^ {2} -2 \ lambda \ left (y- \ hat {x} \ right) ^ {T} \ left (x- \ hat {x} \ right) $

$ \ Rightarrow \ left \ | y- \ hat {x} \ right \ | ^ {2} + \ lambda ^ {2} \ left \ | x- \ hat {x} \ right \ | -2 \ lambda \ left (y- \ hat {x} \ right) ^ {T} \ left (x- \ hat {x} \ right) \ geq \ left \ | y- \ hat {x} \ right \ | ^ {2} $

$ \ Rightarrow 2 \ lambda \ left (y- \ hat {x} \ right) ^ {T} \ left (x- \ hat {x} \ right) \ leq \ lambda ^ 2 \ left \ | x- \ hat {x} \ right \ | ^ 2 $

$ \ Rightarrow \ left (y- \ hat {x} \ right) ^ {T} \ left (x- \ hat {x} \ right) \ leq 0 $

Daher bewiesen.

Sei S eine nicht leere geschlossene, konvexe Menge in $ \ mathbb {R} ^ n $ und $ y \ notin S $. Dann existiert ein Nicht-Null-Vektor $ p $ und ein Skalar $ \ beta $, so dass $ p ^ T y> \ beta $ und $ p ^ T x <\ beta $ für jedes $ x \ in S $

Beweis

Da S nicht leer ist, geschlossene konvexe Menge und $ y \ notin S $, so existiert nach dem nächsten Punktsatz ein eindeutiger Minimierungspunkt $ \ hat {x} \ in S $, so dass

$ \ left (x- \ hat {x} \ right) ^ T \ left (y- \ hat {x} \ right) \ leq 0 \ forall x \ in S $

Sei $ p = \ left (y- \ hat {x} \ right) \ neq 0 $ und $ \ beta = \ hat {x} ^ T \ left (y- \ hat {x} \ right) = p ^ T. \ hat {x} $.

Dann $ \ left (x- \ hat {x} \ right) ^ T \ left (y- \ hat {x} \ right) \ leq 0 $

$ \ Rightarrow \ left (y- \ hat {x} \ right) ^ T \ left (x- \ hat {x} \ right) \ leq 0 $

$ \ Rightarrow \ left (y- \ hat {x} \ right) ^ Tx \ leq \ left (y- \ hat {x} \ right) ^ T \ hat {x} = \ hat {x} ^ T \ left (y- \ hat {x} \ right) $ i, d. h. $ p ^ Tx \ leq \ beta $

Außerdem ist $ p ^ Ty- \ beta = \ left (y- \ hat {x} \ right) ^ Ty- \ hat {x} ^ T \ left (y- \ hat {x} \ right) $

$ = \ left (y- \ hat {x} \ right) ^ T \ left (yx \ right) = \ left \ | y- \ hat {x} \ right \ | ^ {2}> 0 $

$ \ Rightarrow p ^ Ty> \ beta $

Dieser Satz führt zur Trennung von Hyperebenen. Die auf dem obigen Satz basierenden Hyperebenen können wie folgt definiert werden:

Sei $ S_1 $ und $ S_2 $ nicht leere Teilmengen von $ \ mathbb {R} $ und $ H = \ left \ {X: A ^ TX = b \ right \} $ eine Hyperebene.

• Die Hyperebene H soll $ S_1 $ und $ S_2 $ trennen, wenn $ A ^ TX \ leq b \ für alle X \ in S_1 $ und $ A_TX \ geq b \ für alle X \ in S_2 $

• Die Hyperebene H soll $ S_1 $ und $ S_2 $ streng trennen, wenn $ A ^ TX <b \ für alle X \ in S_1 $ und $ A_TX> b \ für alle X \ in S_2 $

• Die Hyperebene H soll $ S_1 $ und $ S_2 $ stark trennen, wenn $ A ^ TX \ leq b \ für alle X \ in S_1 $ und $ A_TX \ geq b + \ varepsilon \ für alle X \ in S_2 $, wobei $ \ varepsilon $ ist ein positiver Skalar.

Eine nicht leere Menge C in $ \ mathbb {R} ^ n $ heißt Kegel mit Scheitelpunkt 0, wenn $ x \ in C \ Rightarrow \ lambda x \ in C \ forall \ lambda \ geq 0 $.

Eine Menge C ist ein konvexer Kegel, wenn sie sowohl konvex als auch konisch ist.

Zum Beispiel $ y = \ left | x \ right | $ ist kein konvexer Kegel, weil er nicht konvex ist.

Aber $ y \ geq \ left | x \ right | $ ist ein konvexer Kegel, weil er sowohl konvex als auch konisch ist.

Note - Ein Kegel C ist genau dann konvex, wenn für $ x, y \ in C, x + y \ in C $.

Beweis

Da C ein Kegel ist, ist für $ x y \ in C \ Rightarrow \ lambda x \ in C $ und $ \ mu y \ in C \: \ forall \: \ lambda \ mu \ geq 0 $

C ist konvex, wenn $ \ lambda x + \ left (1- \ lambda \ right) y \ in C \: \ forall \: \ lambda \ in \ left (0, 1 \ right) $

Da C Kegel ist, $ \ lambda x \ in C $ und $ \ left (1- \ lambda \ right) y \ in C \ Leftrightarrow x, y \ in C $

Somit ist C konvex, wenn $ x + y \ in C $ ist

Im Allgemeinen, wenn $ x_1, x_2 \ in C $, dann $ \ lambda_1x_1 + \ lambda_2x_2 \ in C, \ forall \ lambda_1, \ lambda_2 \ geq 0 $

Beispiele

• Die konische Kombination einer unendlichen Menge von Vektoren in $ \ mathbb {R} ^ n $ ist ein konvexer Kegel.

• Jeder leere Satz ist ein konvexer Kegel.

• Jede lineare Funktion ist ein konvexer Kegel.

• Da eine Hyperebene linear ist, ist sie auch ein konvexer Kegel.

• Geschlossene Halbräume sind ebenfalls konvexe Kegel.

Note - Der Schnittpunkt zweier konvexer Kegel ist ein konvexer Kegel, aber ihre Vereinigung kann ein konvexer Kegel sein oder nicht.

Sei S eine nicht leere Menge in $ \ mathbb {R} ^ n $. Dann ist der mit $ S ^ * $ bezeichnete Polarkegel von S gegeben durch $ S ^ * = \ left \ {p \ in \ mathbb {R. } ^ n, p ^ Tx \ leq 0 \: \ forall x \ in S \ right \} $.

Anmerkung

• Der Polkegel ist immer konvex, auch wenn S nicht konvex ist.

• Wenn S leer ist, ist $ S ^ * = \ mathbb {R} ^ n $.

• Die Polarität kann als Verallgemeinerung der Orthogonalität angesehen werden.

Sei $ C \ subseteq \ mathbb {R} ^ n $ dann der orthogonale Raum von C, bezeichnet mit $ C ^ \ perp = \ left \ {y \ in \ mathbb {R} ^ n: \ left \ langle x, y \ right \ rangle = 0 \ forall x \ in C \ right \} $.

Lemma

Sei $ S, S_1 $ und $ S_2 $ nicht leere Mengen in $ \ mathbb {R} ^ n $, dann sind die folgenden Aussagen wahr -

• $ S ^ * $ ist ein geschlossener konvexer Kegel.

• $ S \ subseteq S ^ {**} $ wobei $ S ^ {**} $ ein Polarkegel von $ S ^ * $ ist.

• $ S_1 \ subseteq S_2 \ Rightarrow S_ {2} ^ {*} \ subseteq S_ {1} ^ {*} $.

Beweis

Step 1 - $ S ^ * = \ left \ {p \ in \ mathbb {R} ^ n, p ^ Tx \ leq 0 \: \ forall \: x \ in S \ right \} $

• Sei $ x_1, x_2 \ in S ^ * \ Rightarrow x_ {1} ^ {T} x \ leq 0 $ und $ x_ {2} ^ {T} x \ leq 0, \ forall x \ in S $

  Für $ \ lambda \ in \ left (0, 1 \ right), \ left [\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right] ^ Tx = \ left [\ left (\ lambda x_1 \ right) ) ^ T + \ left \ {\ left (1- \ lambda \ right) x_ {2} \ right \} ^ {T} \ right] x, \ forall x \ in S $

  $ = \ left [\ lambda x_ {1} ^ {T} + \ left (1- \ lambda \ right) x_ {2} ^ {T} \ right] x = \ lambda x_ {1} ^ {T} x + \ left (1- \ lambda \ right) x_ {2} ^ {T} \ leq 0 $

  Also $ \ lambda x_1 + \ left (1- \ lambda \ right) x_ {2} \ in S ^ * $

  Daher ist $ S ^ * $ eine konvexe Menge.

• Für $ \ lambda \ geq 0 ist p ^ {T} x \ leq 0, \ forall \: x \ in S $

  Daher ist $ \ lambda p ^ T x \ leq 0, $

  $ \ Rightarrow \ left (\ lambda p \ right) ^ T x \ leq 0 $

  $ \ Rightarrow \ lambda p \ in S ^ * $

  Somit ist $ S ^ * $ ein Kegel.

• Das Anzeigen von $ S ^ * $ ist geschlossen, dh das Anzeigen von $ p_n \ rightarrow p $ als $ n \ rightarrow \ infty $, dann $ p \ in S ^ * $

  $ \ forall x \ in S, p_ {n} ^ {T} xp ^ T x = \ left (p_n-p \ right) ^ T x $

  Als $ p_n \ rightarrow p $ als $ n \ rightarrow \ infty \ Rightarrow \ left (p_n \ rightarrow p \ right) \ rightarrow 0 $

  Daher $ p_ {n} ^ {T} x \ rightarrow p ^ {T} x $. Aber $ p_ {n} ^ {T} x \ leq 0, \: \ forall x \ in S $

  Somit ist $ p ^ Tx \ leq 0, \ forall x \ in S $

  $ \ Rightarrow p \ in S ^ * $

  Daher ist $ S ^ * $ geschlossen.

Step 2 - $ S ^ {**} = \ left \ {q \ in \ mathbb {R} ^ n: q ^ T p \ leq 0, \ forall p \ in S ^ * \ right \} $

Sei $ x \ in S $, dann $ \ forall p \ in S ^ *, p ^ T x \ leq 0 \ Rightarrow x ^ Tp \ leq 0 \ Rightarrow x \ in S ^ {**} $

Somit ist $ S \ subseteq S ^ {**} $

Step 3 - $ S_2 ^ * = \ left \ {p \ in \ mathbb {R} ^ n: p ^ Tx \ leq 0, \ forall x \ in S_2 \ right \} $

Da $ S_1 \ subseteq S_2 \ Rightarrow \ forall x \ in S_2 \ Rightarrow \ forall x \ in S_1 $

Wenn also $ \ hat {p} \ in S_2 ^ *, dann $ \ hat {p} ^ Tx \ leq 0, \ forall x \ in S_2 $

$ \ Rightarrow \ hat {p} ^ Tx \ leq 0, \ forall x \ in S_1 $

$ \ Rightarrow \ hat {p} ^ T \ in S_1 ^ * $

$ \ Rightarrow S_2 ^ * \ subseteq S_1 ^ * $

Satz

Sei C ein nicht leerer geschlossener konvexer Kegel, dann ist $ C = C ^ ** $

Beweis

$ C = C ^ {**} $ nach vorherigem Lemma.

Zum Beweis: $ x \ in C ^ {**} \ subseteq C $

Lassen Sie $ x \ in C ^ {**} $ und lassen Sie $ x \ notin C $

Dann existiert nach dem fundamentalen Trennungssatz ein Vektor $ p \ neq 0 $ und ein Skalar $ \ alpha $, so dass $ p ^ Ty \ leq \ alpha, \ forall y \ in C $

Daher ist $ p ^ Tx> \ alpha $

Aber da $ \ left (y = 0 \ right) \ in C $ und $ p ^ Ty \ leq \ alpha, \ forall y \ in C \ Rightarrow \ alpha \ geq 0 $ und $ p ^ Tx> 0 $

Wenn $ p \ notin C ^ * $ ist, existiert in C $ ein $ \ bar {y} \, so dass $ p ^ T \ bar {y}> 0 $ und $ p ^ T \ left (\ lambda \ bar) {y} \ right) $ kann beliebig groß gemacht werden, indem $ \ lambda $ ausreichend groß genommen wird.

Dies widerspricht der Tatsache, dass $ p ^ Ty \ leq \ alpha, \ forall y \ in C $

Daher $ p \ in C ^ * $

Da $ x \ in C ^ * = \ left \ {q: q ^ Tp \ leq 0, \ forall p \ in C ^ * \ right \} $

Daher ist $ x ^ Tp \ leq 0 \ Rightarrow p ^ Tx \ leq 0 $

Aber $ p ^ Tx> \ alpha $

So ist Widerspruch.

Also $ x \ in C $

Daher ist $ C = C ^ {**} $.

Ein Punkt der Form $ \ alpha_1x_1 + \ alpha_2x_2 + .... + \ alpha_nx_n $ mit $ \ alpha_1, \ alpha_2, ..., \ alpha_n \ geq 0 $ heißt konische Kombination von $ x_1, x_2, ..., x_n. $

• Wenn sich $ x_i $ im konvexen Kegel C befindet, befindet sich jede konische Kombination von $ x_i $ auch in C.

• Eine Menge C ist ein konvexer Kegel, wenn sie die gesamte konische Kombination ihrer Elemente enthält.

Kegelrumpf

Eine Kegelhülle ist definiert als eine Menge aller Kegelkombinationen einer gegebenen Menge S und wird mit Kegel (S) bezeichnet.

Somit ist $ coni \ left (S \ right) = \ left \ {\ displaystyle \ sum \ border_ {i = 1} ^ k \ lambda_ix_i: x_i \ in S, \ lambda_i \ in \ mathbb {R}, \ lambda_i \ geq 0, i = 1,2, ... \ right \} $

• Der konische Rumpf ist ein konvexer Satz.
• Der Ursprung liegt immer in der konischen Hülle.

Eine Menge in $ \ mathbb {R} ^ n $ wird als polyedrisch bezeichnet, wenn es sich um den Schnittpunkt einer endlichen Anzahl geschlossener halber Räume handelt, d. H.

$ S = \ left \ {x \ in \ mathbb {R} ^ n: p_ {i} ^ {T} x \ leq \ alpha_i, i = 1,2, ...., n \ right \} $

Zum Beispiel,

• $ \ left \ {x \ in \ mathbb {R} ^ n: AX = b \ right \} $

• $ \ left \ {x \ in \ mathbb {R} ^ n: AX \ leq b \ right \} $

• $ \ left \ {x \ in \ mathbb {R} ^ n: AX \ geq b \ right \} $

Polyedrischer Kegel

Eine Menge in $ \ mathbb {R} ^ n $ wird als polyedrischer Kegel bezeichnet, wenn es sich um den Schnittpunkt einer endlichen Anzahl von Halbräumen handelt, die den Ursprung enthalten, dh $ S = \ left \ {x \ in \ mathbb { R} ^ n: p_ {i} ^ {T} x \ leq 0, i = 1, 2, ... \ right \} $

Polytop

Ein Polytop ist eine polyedrische Menge, die begrenzt ist.

Bemerkungen

• Ein Polytop ist eine konvexe Hülle einer endlichen Menge von Punkten.
• Ein polyedrischer Kegel wird durch eine endliche Menge von Vektoren erzeugt.
• Eine polyedrische Menge ist eine geschlossene Menge.
• Eine polyedrische Menge ist eine konvexe Menge.

Sei S eine konvexe Menge in $ \ mathbb {R} ^ n $. Ein Vektor $ x \ in S $ wird als Extrempunkt von S bezeichnet, wenn $ x = \ lambda x_1 + \ left (1- \ lambda \ right) x_2 $ mit $ x_1, x_2 \ in S $ und $ \ lambda \ in \ left (0, 1 \ right) \ Rightarrow x = x_1 = x_2 $.

Beispiel

Step 1 - $ S = \ left \ {\ left (x_1, x_2 \ right) \ in \ mathbb {R} ^ 2: x_ {1} ^ {2} + x_ {2} ^ {2} \ leq 1 \ right \ } $

Extrempunkt, $ E = \ left \ {\ left (x_1, x_2 \ right) \ in \ mathbb {R} ^ 2: x_ {1} ^ {2} + x_ {2} ^ {2} = 1 \ right \} $

Step 2 - $ S = \ left \ {\ left (x_1, x_2 \ right) \ in \ mathbb {R} ^ 2: x_1 + x_2 <2, -x_1 + 2x_2 \ leq 2, x_1, x_2 \ geq 0 \ right \ } $

Extrempunkt, $ E = \ left \ {\ left (0, 0 \ right), \ left (2, 0 \ right), \ left (0, 1 \ right), \ left (\ frac {2} {3 }, \ frac {4} {3} \ right) \ right \} $

Step 3 - S ist das Polytop, das aus den Punkten $ \ left \ {\ left (0,0 \ right), \ left (1,1 \ right), \ left (1,3 \ right), \ left (-2, 4 \ rechts), \ links (0,2 \ rechts) \ rechts \} $

Extrempunkt, $ E = \ left \ {\ left (0,0 \ right), \ left (1,1 \ right), \ left (1,3 \ right), \ left (-2,4 \ right) \ right \} $

Bemerkungen

• Jeder Punkt der konvexen Menge S kann als konvexe Kombination seiner Extrempunkte dargestellt werden.

• Dies gilt nur für geschlossene und begrenzte Mengen in $ \ mathbb {R} ^ n $.

• Dies gilt möglicherweise nicht für unbegrenzte Mengen.

k Extrempunkte

Ein Punkt in einer konvexen Menge wird genau dann als k extrem bezeichnet, wenn er der innere Punkt einer k-dimensionalen konvexen Menge innerhalb von S ist und kein innerer Punkt einer (k + 1) - dimensionalen konvexen Menge innerhalb von S. Grundsätzlich ergeben k Extrempunkte für eine konvexe Menge S k-dimensionale offene Flächen.

Sei S eine geschlossene konvexe Menge in $ \ mathbb {R} ^ n $. Ein Nicht-Null-Vektor $ d \ in \ mathbb {R} ^ n $ wird als Richtung von S bezeichnet, wenn für jedes $ x \ in S x + \ lambda d \ in S \ forall \ lambda \ geq 0. $

• Zwei Richtungen $ d_1 $ und $ d_2 $ von S werden als verschieden bezeichnet, wenn $ d \ neq \ alpha d_2 $ für $ \ alpha> 0 $ ist.

• Eine Richtung $ d $ von $ S $ wird als extreme Richtung bezeichnet, wenn sie nicht als positive lineare Kombination zweier unterschiedlicher Richtungen geschrieben werden kann, dh wenn $ d = \ lambda _1d_1 + \ lambda _2d_2 $ für $ \ lambda _1, \ Lambda _2> 0 $, dann $ d_1 = \ alpha d_2 $ für einige $ \ alpha $.

• Jede andere Richtung kann als positive Kombination extremer Richtungen ausgedrückt werden.

• Für eine konvexe Menge $ S $ wird die Richtung d so aufgerufen, dass $ x + \ lambda d \ in S $ für einige $ x \ in S $ und alle $ \ lambda \ geq0 $ aufgerufen wird recessive für $ S $.

• Sei E die Menge der Punkte, an denen eine bestimmte Funktion $ f: S \ rightarrow $ über einer nicht leeren konvexen Menge S in $ \ mathbb {R} ^ n $ ihr Maximum erreicht, dann heißt $ E $ exponierte Fläche von $ S $. Die Richtungen der belichteten Flächen werden als belichtete Richtungen bezeichnet.

• Ein Strahl, dessen Richtung eine extreme Richtung ist, wird als extremer Strahl bezeichnet.

Beispiel

Betrachten Sie die Funktion $ f \ left (x \ right) = y = \ left | x \ right | $, wobei $ x \ in \ mathbb {R} ^ n $. Sei d ein Einheitsvektor in $ \ mathbb {R} ^ n $

Dann ist d die Richtung für die Funktion f, weil für jedes $ \ lambda \ geq 0 x + \ lambda d \ in f \ left (x \ right) $.

Sei $ f: S \ rightarrow \ mathbb {R} $, wobei S nicht leer ist, konvex in $ \ mathbb {R} ^ n $ gesetzt, dann wird $ f \ left (x \ right) $ auf S als konvex bezeichnet wenn $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left ( x_2 \ rechts), \ forall \ lambda \ in \ links (0,1 \ rechts) $.

Auf der anderen Seite sei $ f: S \ rightarrow \ mathbb {R} $, wobei S nicht leer ist, konvex in $ \ mathbb {R} ^ n $ gesetzt, dann wird $ f \ left (x \ right) $ gesagt auf S konkav sein, wenn $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ geq \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) ) f \ left (x_2 \ right), \ forall \ lambda \ in \ left (0, 1 \ right) $.

Sei $ f: S \ rightarrow \ mathbb {R} $, wobei S nicht leer ist, konvex in $ \ mathbb {R} ^ n $ gesetzt, dann wird $ f \ left (x \ right) $ auf S als streng konvex bezeichnet wenn $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) <\ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2) \ rechts), \ forall \ lambda \ in \ links (0, 1 \ rechts) $.

Sei $ f: S \ rightarrow \ mathbb {R} $, wobei S nicht leer ist, konvex in $ \ mathbb {R} ^ n $ gesetzt, dann soll $ f \ left (x \ right) $ auf S streng konkav sein wenn $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right)> \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2) \ rechts), \ forall \ lambda \ in \ links (0, 1 \ rechts) $.

Beispiele

• Eine lineare Funktion ist sowohl konvex als auch konkav.

• $ f \ left (x \ right) = \ left | x \ right | $ ist eine konvexe Funktion.

• $ f \ left (x \ right) = \ frac {1} {x} $ ist eine konvexe Funktion.

Satz

Sei $ f_1, f_2, ..., f_k: \ mathbb {R} ^ n \ rightarrow \ mathbb {R} $ konvexe Funktionen. Betrachten Sie die Funktion $ f \ left (x \ right) = \ displaystyle \ sum \ limit_ {j = 1} ^ k \ alpha_jf_j \ left (x \ right) $, wobei $ \ alpha_j> 0, j = 1, 2 ,. ..k, $ then $ f \ left (x \ right) $ ist eine konvexe Funktion.

Beweis

Da $ f_1, f_2, ... f_k $ konvexe Funktionen sind

Daher ist $ f_i \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda f_i \ left (x_1 \ right) + \ left (1- \ lambda \ right) f_i \ left (x_2 \ rechts), \ forall \ lambda \ in \ links (0, 1 \ rechts) $ und $ i = 1, 2, ...., k $

Betrachten Sie die Funktion $ f \ left (x \ right) $.

Deshalb,

$ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) $

$ = \ Anzeigestil \ Summe \ Grenzen_ {j = 1} ^ k \ alpha_jf_j \ links (\ lambda x_1 + 1- \ lambda \ rechts) x_2 \ leq \ Anzeigestil \ Summe \ Grenzen_ {j = 1} ^ k \ alpha_j \ Lambda f_j \ links (x_1 \ rechts) + \ links (1- \ Lambda \ rechts) f_j \ links (x_2 \ rechts) $

$ \ Rightarrow f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda \ left (\ displaystyle \ sum \ limit_ {j = 1} ^ k \ alpha _jf_j \ left ( x_1 \ rechts) \ rechts) + \ links (\ Anzeigestil \ Summe \ Grenzen_ {j = 1} ^ k \ alpha _jf_j \ links (x_2 \ rechts) \ rechts) $

$ \ Rightarrow f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda f \ left (x_2 \ right) \ leq \ left (1- \ lambda \ right) f \ left (x_2 \ right) $

Daher ist $ f \ left (x \ right) $ eine konvexe Funktion.

Satz

Sei $ f \ left (x \ right) $ eine konvexe Funktion auf einer konvexen Menge $ S \ subset \ mathbb {R} ^ n $, dann ist ein lokales Minimum von $ f \ left (x \ right) $ auf S a globale Minima.

Beweis

Sei $ \ hat {x} $ ein lokales Minimum für $ f \ left (x \ right) $ und $ \ hat {x} $ ist kein globales Minimum.

Daher existiert $ \ \ hat {x} \ in S $, so dass $ f \ left (\ bar {x} \ right) <f \ left (\ hat {x} \ right) $

Da $ \ hat {x} $ ein lokales Minimum ist, existiert die Nachbarschaft $ N_ \ varepsilon \ left (\ hat {x} \ right) $, so dass $ f \ left (\ hat {x} \ right) \ leq f \ left (x \ right), \ forall x \ in N_ \ varepsilon \ left (\ hat {x} \ right) \ cap S $

But $f\left ( x \right )$ is a convex function on S, therefore for $\lambda \in \left ( 0, 1 \right )$

we have $\lambda \hat{x}+\left ( 1-\lambda \right )\bar{x}\leq \lambda f\left ( \hat{x} \right )+\left ( 1-\lambda \right )f\left ( \bar{x} \right )$

$\Rightarrow \lambda \hat{x}+\left ( 1-\lambda \right )\bar{x}< \lambda f\left ( \hat{x} \right )+\left ( 1-\lambda \right )f\left (\hat{x} \right )$

$\Rightarrow \lambda \hat{x}+\left ( 1-\lambda \right )\bar{x}< f\left (\hat{x} \right ), \forall \lambda \in \left ( 0,1 \right )$

But for some $\lambda<1$ but close to 1, we have

$\lambda \hat{x}+\left ( 1-\lambda \right )\bar{x} \in N_\varepsilon \left ( \hat{x} \right )\cap S$ and $f\left ( \lambda \hat{x}+\left ( 1-\lambda \right )\bar{x} \right )< f\left ( \bar{x} \right )$

which is a contradiction.

Hence, $\bar{x}$ is a global minima.

Epigraph

let S be a non-empty subset in $\mathbb{R}^n$ and let $f:S \rightarrow \mathbb{R}$ then the epigraph of f denoted by epi(f) or $E_f$ is a subset of $\mathbb{R}^n+1$ defined by $E_f=\left \{ \left ( x,\alpha \right ):x \in \mathbb{R}^n, \alpha \in \mathbb{R}, f\left ( x \right )\leq \alpha \right \}$

Hypograph

let S be a non-empty subset in $\mathbb{R}^n$ and let $f:S \rightarrow \mathbb{R}$, then the hypograph of f denoted by hyp(f) or $H_f=\left \{ \left ( x, \alpha \right ):x \in \mathbb{R}^n, \alpha \in \mathbb{R}^n, \alpha \in \mathbb{R}, f\left ( x \right )\geq \alpha \right \}$

Theorem

Let S be a non-empty convex set in $\mathbb{R}^n$ and let $f:S \rightarrow \mathbb{R}^n$, then f is convex if and only if its epigraph $E_f$ is a convex set.

Proof

Let f is a convex function.

To show $E_f$ is a convex set.

Let $\left ( x_1, \alpha_1 \right ),\left ( x_2, \alpha_2 \right ) \in E_f,\lambda \in\left ( 0, 1 \right )$

To show $\lambda \left ( x_1,\alpha_1 \right )+\left ( 1-\lambda \right )\left ( x_2, \alpha_2 \right ) \in E_f$

$\Rightarrow \left [ \lambda x_1+\left ( 1-\lambda \right )x_2, \lambda \alpha_1+\left ( 1-\lambda \right )\alpha_2 \right ]\in E_f$

$f\left ( x_1 \right )\leq \alpha _1, f\left ( x_2\right )\leq \alpha _2$

Therefore, $f\left (\lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f \left ( x_2 \right )$

$\Rightarrow f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq \lambda \alpha_1+\left ( 1-\lambda \right )\alpha_2$

Converse

Let $E_f$ is a convex set.

To show f is convex.

i.e., to show if $x_1, x_2 \in S,\lambda \left ( 0, 1\right )$

$f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f\left ( x_2 \right )$

Let $x_1,x_2 \in S, \lambda \in \left ( 0, 1 \right ),f\left ( x_1 \right ), f\left ( x_2 \right ) \in \mathbb{R}$

Since $E_f$ is a convex set, $\left ( \lambda x_1+\left ( 1-\lambda \right )x_2, \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )\right )f\left ( x_2 \right )\in E_f$

Therefore, $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f\left ( x_2 \right )$

Let S be a non-empty convex set in $\mathbb{R}^n$ and $f:S \rightarrow \mathbb{R}^n$. Then f is convex if and only if for each integer $k>0$

$x_1,x_2,...x_k \in S, \displaystyle\sum\limits_{i=1}^k \lambda_i=1, \lambda_i\geq 0, \forall i=1,2,s,k$, we have $f\left ( \displaystyle\sum\limits_{i=1}^k \lambda_ix_i \right )\leq \displaystyle\sum\limits_{i=1}^k \lambda _if\left ( x \right )$

Proof

By induction on k.

$k=1:x_1 \in S$ Therefore $f\left ( \lambda_1 x_1\right ) \leq \lambda_i f\left (x_1\right )$ because $\lambda_i=1$.

$k=2:\lambda_1+\lambda_2=1$ and $x_1, x_2 \in S$

Therefore, $\lambda_1x_1+\lambda_2x_2 \in S$

Hence by definition, $f\left ( \lambda_1 x_1 +\lambda_2 x_2 \right )\leq \lambda _1f\left ( x_1 \right )+\lambda _2f\left ( x_2 \right )$

Let the statement is true for $n < k$

Therefore,

$f\left ( \lambda_1 x_1+ \lambda_2 x_2+....+\lambda_k x_k\right )\leq \lambda_1 f\left (x_1 \right )+\lambda_2 f\left (x_2 \right )+...+\lambda_k f\left (x_k \right )$

$k=n+1:$ Let $x_1, x_2,....x_n,x_{n+1} \in S$ and $\displaystyle\sum\limits_{i=1}^{n+1}=1$

Therefore $\mu_1x_1+\mu_2x_2+.......+\mu_nx_n+\mu_{n+1} x_{n+1} \in S$

thus,$f\left (\mu_1x_1+\mu_2x_2+...+\mu_nx_n+\mu_{n+1} x_{n+1} \right )$

$=f\left ( \left ( \mu_1+\mu_2+...+\mu_n \right)\frac{\mu_1x_1+\mu_2x_2+...+\mu_nx_n}{\mu_1+\mu_2+\mu_3}+\mu_{n+1}x_{n+1} \right)$

$=f\left ( \mu_y+\mu_{n+1}x_{n+1} \right )$ where $\mu=\mu_1+\mu_2+...+\mu_n$ and

$y=\frac{\mu_1x_1+\mu_2x_2+...+\mu_nx_n}{\mu_1+\mu_2+...+\mu_n}$ and also $\mu_1+\mu_{n+1}=1,y \in S$

$\Rightarrow f\left ( \mu_1x_1+\mu_2x_2+...+\mu_nx_n+\mu_{n+1}x_{n+1}\right ) \leq \mu f\left ( y \right )+\mu_{n+1} f\left ( x_{n+1} \right )$

$\Rightarrow f\left ( \mu_1x_1+\mu_2x_2+...+\mu_nx_n+\mu_{n+1}x_{n+1}\right ) \leq$

$\left ( \mu_1+\mu_2+...+\mu_n \right )f\left ( \frac{\mu_1x_1+\mu_2x_2+...+\mu_nx_n}{\mu_1+\mu_2+...+\mu_n} \right )+\mu_{n+1}f\left ( x_{n+1} \right )$

$\Rightarrow f\left ( \mu_1x_1+\mu_2x_2+...+\mu_nx_n +\mu_{n+1}x_{n+1}\right )\leq \left ( \mu_1+ \mu_2+ ...+\mu_n \right )$

$\left [ \frac{\mu_1}{\mu_1+ \mu_2+ ...+\mu_n}f\left ( x_1 \right )+...+\frac{\mu_n}{\mu_1+ \mu_2+ ...+\mu_n}f\left ( x_n \right ) \right ]+\mu_{n+1}f\left ( x_{n+1} \right )$

$\Rightarrow f\left ( \mu_1x_1+\mu_2x_2+...+\mu_nx_n+\mu_{n+1}x_{n+1}\right )\leq \mu_1f\left ( x_1 \right )+\mu_2f\left ( x_2 \right )+....$

Hence Proved.

Let S be a non-empty open set in $\mathbb{R}^n$,then $f:S\rightarrow \mathbb{R}$ is said to be differentiable at $\hat{x} \in S$ if there exist a vector $\bigtriangledown f\left ( \hat{x} \right )$ called gradient vector and a function $\alpha :\mathbb{R}^n\rightarrow \mathbb{R}$ such that

$f\left ( x \right )=f\left ( \hat{x} \right )+\bigtriangledown f\left ( \hat{x} \right )^T\left ( x-\hat{x} \right )+\left \| x=\hat{x} \right \|\alpha \left ( \hat{x}, x-\hat{x} \right ), \forall x \in S$ where

$\alpha \left (\hat{x}, x-\hat{x} \right )\rightarrow 0 \bigtriangledown f\left ( \hat{x} \right )=\left [ \frac{\partial f}{\partial x_1}\frac{\partial f}{\partial x_2}...\frac{\partial f}{\partial x_n} \right ]_{x=\hat{x}}^{T}$

Theorem

let S be a non-empty, open convexset in $\mathbb{R}^n$ and let $f:S\rightarrow \mathbb{R}$ be differentiable on S. Then, f is convex if and only if for $x_1,x_2 \in S, \bigtriangledown f\left ( x_2 \right )^T \left ( x_1-x_2 \right ) \leq f\left ( x_1 \right )-f\left ( x_2 \right )$

Proof

Let f be a convex function. i.e., for $x_1,x_2 \in S, \lambda \in \left ( 0, 1 \right )$

$f\left [ \lambda x_1+\left ( 1-\lambda \right )x_2 \right ]\leq \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f\left ( x_2 \right )$

$ \Rightarrow f\left [ \lambda x_1+\left ( 1-\lambda \right )x_2 \right ]\leq \lambda \left ( f\left ( x_1 \right )-f\left ( x_2 \right ) \right )+f\left ( x_2 \right )$

$ \Rightarrow\lambda \left ( f\left ( x_1 \right )-f\left ( x_2 \right ) \right )\geq f\left ( x_2+\lambda \left ( x_1-x_2 \right ) \right )-f\left ( x_2 \right )$

$\Rightarrow \lambda \left ( f\left ( x_1 \right )-f\left ( x_2 \right ) \right )\geq f\left ( x_2 \right )+\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )\lambda +$

$\left \| \lambda \left ( x_1-x_2 \right ) \right \|\alpha \left ( x_2,\lambda\left (x_1 - x_2 \right )-f\left ( x_2 \right ) \right )$

where $\alpha\left ( x_2, \lambda\left (x_1 - x_2 \right ) \right )\rightarrow 0$ as$\lambda \rightarrow 0$

Dividing by $\lambda$ on both sides, we get −

$f\left ( x_1 \right )-f\left ( x_2 \right ) \geq \bigtriangledown f\left ( x_2 \right )^T \left ( x_1-x_2 \right )$

Converse

Let for $x_1,x_2 \in S, \bigtriangledown f\left ( x_2 \right )^T \left ( x_1-x_2 \right ) \leq f\left ( x_1 \right )-f \left ( x_2 \right )$

To show that f is convex.

Since S is convex, $x_3=\lambda x_1+\left (1-\lambda \right )x_2 \in S, \lambda \in \left ( 0, 1 \right )$

Since $x_1, x_3 \in S$, therefore

$f\left ( x_1 \right )-f \left ( x_3 \right ) \geq \bigtriangledown f\left ( x_3 \right )^T \left ( x_1 -x_3\right )$

$ \Rightarrow f\left ( x_1 \right )-f \left ( x_3 \right )\geq \bigtriangledown f\left ( x_3 \right )^T \left ( x_1 - \lambda x_1-\left (1-\lambda \right )x_2\right )$

$ \Rightarrow f\left ( x_1 \right )-f \left ( x_3 \right )\geq \left ( 1- \lambda\right )\bigtriangledown f\left ( x_3 \right )^T \left ( x_1 - x_2\right )$

Since, $x_2, x_3 \in S$ therefore

$f\left ( x_2 \right )-f\left ( x_3 \right )\geq \bigtriangledown f\left ( x_3 \right )^T\left ( x_2-x_3 \right )$

$\Rightarrow f\left ( x_2 \right )-f\left ( x_3 \right )\geq \bigtriangledown f\left ( x_3 \right )^T\left ( x_2-\lambda x_1-\left ( 1-\lambda \right )x_2 \right )$

$\Rightarrow f\left ( x_2 \right )-f\left ( x_3 \right )\geq \left ( -\lambda \right )\bigtriangledown f\left ( x_3 \right )^T\left ( x_1-x_2 \right )$

Thus, combining the above equations, we get −

$\lambda \left ( f\left ( x_1 \right )-f\left ( x_3 \right ) \right )+\left ( 1- \lambda \right )\left ( f\left ( x_2 \right )-f\left ( x_3 \right ) \right )\geq 0$

$\Rightarrow f\left ( x_3\right )\leq \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f\left ( x_2 \right )$

Theorem

let S be a non-empty open convex set in $\mathbb{R}^n$ and let $f:S \rightarrow \mathbb{R}$ be differentiable on S, then f is convex on S if and only if for any $x_1,x_2 \in S,\left ( \bigtriangledown f \left ( x_2 \right )-\bigtriangledown f \left ( x_1 \right ) \right )^T \left ( x_2-x_1 \right ) \geq 0$

Proof

let f be a convex function, then using the previous theorem −

$\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )\leq f\left ( x_1 \right )-f\left ( x_2 \right )$ and

$\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\leq f\left ( x_2 \right )-f\left ( x_1 \right )$

Adding the above two equations, we get −

$\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )+\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\leq 0$

$\Rightarrow \left ( \bigtriangledown f\left ( x_2 \right )-\bigtriangledown f\left ( x_1 \right ) \right )^T\left ( x_1-x_2 \right )\leq 0$

$\Rightarrow \left ( \bigtriangledown f\left ( x_2 \right )-\bigtriangledown f\left ( x_1 \right ) \right )^T\left ( x_2-x_1 \right )\geq 0$

Converse

Let for any $x_1,x_2 \in S,\left (\bigtriangledown f \left ( x_2\right )- \bigtriangledown f \left ( x_1\right )\right )^T \left ( x_2-x_1\right )\geq 0$

To show that f is convex.

Let $x_1,x_2 \in S$, thus by mean value theorem, $\frac{f\left ( x_1\right )-f\left ( x_2\right )}{x_1-x_2}=\bigtriangledown f\left ( x\right ),x \in \left ( x_1-x_2\right ) \Rightarrow x= \lambda x_1+\left ( 1-\lambda\right )x_2$ because S is a convex set.

$\Rightarrow f\left ( x_1 \right )- f\left ( x_2 \right )=\left ( \bigtriangledown f\left ( x \right )^T \right )\left ( x_1-x_2 \right )$

for $x,x_1$, we know −

$\left ( \bigtriangledown f\left ( x \right )-\bigtriangledown f\left ( x_1 \right ) \right )^T\left ( x-x_1 \right )\geq 0$

$\Rightarrow \left ( \bigtriangledown f\left ( x \right )-\bigtriangledown f\left ( x_1 \right ) \right )^T\left ( \lambda x_1+\left ( 1-\lambda \right )x_2-x_1 \right )\geq 0$

$\Rightarrow \left ( \bigtriangledown f\left ( x \right )- \bigtriangledown f\left ( x_1 \right )\right )^T\left ( 1- \lambda \right )\left ( x_2-x_1 \right )\geq 0$

$\Rightarrow \bigtriangledown f\left ( x \right )^T\left ( x_2-x_1 \right )\geq \bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )$

Combining the above equations, we get −

$\Rightarrow \bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\leq f\left ( x_2 \right )-f\left ( x_1 \right )$

Hence using the last theorem, f is a convex function.

Twice Differentiable function

Let S be a non-empty subset of $\mathbb{R}^n$ and let $f:S\rightarrow \mathbb{R}$ then f is said to be twice differentiable at $\bar{x} \in S$ if there exists a vector $\bigtriangledown f\left (\bar{x}\right ), a \:nXn$ matrix $H\left (x\right )$(called Hessian matrix) and a function $\alpha:\mathbb{R}^n \rightarrow \mathbb{R}$ such that $f\left ( x \right )=f\left ( \bar{x}+x-\bar{x} \right )=f\left ( \bar{x} \right )+\bigtriangledown f\left ( \bar{x} \right )^T\left ( x-\bar{x} \right )+\frac{1}{2}\left ( x-\bar{x} \right )H\left ( \bar{x} \right )\left ( x-\bar{x} \right )$

where $ \alpha \left ( \bar{x}, x-\bar{x} \right )\rightarrow Oasx\rightarrow \bar{x}$

Theorem

Let f be twice differentiable function. If $\bar{x}$ is a local minima, then $\bigtriangledown f\left ( \bar{x} \right )=0$ and the Hessian matrix $H\left ( \bar{x} \right )$ is a positive semidefinite.

Proof

Let $d \in \mathbb{R}^n$. Since f is twice differentiable at $\bar{x}$.

Therefore,

$f\left ( \bar{x} +\lambda d\right )=f\left ( \bar{x} \right )+\lambda \bigtriangledown f\left ( \bar{x} \right )^T d+\lambda^2d^TH\left ( \bar{x} \right )d+\lambda^2d^TH\left ( \bar{x} \right )d+$

$\lambda^2\left \| d \right \|^2\beta \left ( \bar{x}, \lambda d \right )$

But $\bigtriangledown f\left ( \bar{x} \right )=0$ and $\beta\left ( \bar{x}, \lambda d \right )\rightarrow 0$ as $\lambda \rightarrow 0$

$\Rightarrow f\left ( \bar{x} +\lambda d \right )-f\left ( \bar{x} \right )=\lambda ^2d^TH\left ( \bar{x} \right )d$

Since $\bar{x }$ is a local minima, there exists a $\delta > 0$ such that $f\left ( x \right )\leq f\left ( \bar{x}+\lambda d \right ), \forall \lambda \in \left ( 0,\delta \right )$

Theorem

Let $f:S \rightarrow \mathbb{R}^n$ where $S \subset \mathbb{R}^n$ be twice differentiable over S. If $\bigtriangledown f\left ( x\right )=0$ and $H\left ( \bar{x} \right )$ is positive semi-definite, for all $x \in S$, then $\bar{x}$ is a global optimal solution.

Proof

Since $H\left ( \bar{x} \right )$ is positive semi-definite, f is convex function over S. Since f is differentiable and convex at $\bar{x}$

$\bigtriangledown f\left ( \bar{x} \right )^T \left ( x-\bar{x} \right ) \leq f\left (x\right )-f\left (\bar{x}\right ),\forall x \in S$

Since $\bigtriangledown f\left ( \bar{x} \right )=0, f\left ( x \right )\geq f\left ( \bar{x} \right )$

Hence, $\bar{x}$ is a global optima.

Theorem

Suppose $\bar{x} \in S$ is a local optimal solution to the problem $f:S \rightarrow \mathbb{R}$ where S is a non-empty subset of $\mathbb{R}^n$ and S is convex. $min \:f\left ( x \right )$ where $x \in S$.

Then:

• $\bar{x}$ is a global optimal solution.

• If either $\bar{x}$ is strictly local minima or f is strictly convex function, then $\bar{x}$ is the unique global optimal solution and is also strong local minima.

Proof

Let $\bar{x}$ be another global optimal solution to the problem such that $x \neq \bar{x}$ and $f\left ( \bar{x} \right )=f\left ( \hat{x} \right )$

Since $\hat{x},\bar{x} \in S$ and S is convex, then $\frac{\hat{x}+\bar{x}}{2} \in S$ and f is strictly convex.

$\Rightarrow f\left ( \frac{\hat{x}+\bar{x}}{2} \right )< \frac{1}{2} f\left (\bar{x}\right )+\frac{1}{2} f\left (\hat{x}\right )=f\left (\hat{x}\right )$

This is contradiction.

Hence, $\hat{x}$ is a unique global optimal solution.

Corollary

Let $f:S \subset \mathbb{R}^n \rightarrow \mathbb{R}$ be a differentiable convex function where $\phi \neq S\subset \mathbb{R}^n$ is a convex set. Consider the problem $min f\left (x\right ),x \in S$,then $\bar{x}$ is an optimal solution if $\bigtriangledown f\left (\bar{x}\right )^T\left (x-\bar{x}\right ) \geq 0,\forall x \in S.$

Proof

Let $\bar{x}$ is an optimal solution, i.e, $f\left (\bar{x}\right )\leq f\left (x\right ),\forall x \in S$

$\Rightarrow f\left (x\right )=f\left (\bar{x}\right )\geq 0$

$f\left (x\right )=f\left (\bar{x}\right )+\bigtriangledown f\left (\bar{x}\right )^T\left (x-\bar{x}\right )+\left \| x-\bar{x} \right \|\alpha \left ( \bar{x},x-\bar{x} \right )$

where $\alpha \left ( \bar{x},x-\bar{x} \right )\rightarrow 0$ as $x \rightarrow \bar{x}$

$\Rightarrow f\left (x\right )-f\left (\bar{x}\right )=\bigtriangledown f\left (\bar{x}\right )^T\left (x-\bar{x}\right )\geq 0$

Corollary

Let f be a differentiable convex function at $\bar{x}$,then $\bar{x}$ is global minimum iff $\bigtriangledown f\left (\bar{x}\right )=0$

Examples

• $f\left (x\right )=\left (x^2-1\right )^{3}, x \in \mathbb{R}$.

  $\bigtriangledown f\left (x\right )=0 \Rightarrow x= -1,0,1$.

  $\bigtriangledown^2f\left (\pm 1 \right )=0, \bigtriangledown^2 f\left (0 \right )=6>0$.

  $f\left (\pm 1 \right )=0,f\left (0 \right )=-1$

  Hence, $f\left (x \right ) \geq -1=f\left (0 \right )\Rightarrow f\left (0 \right ) \leq f \left (x \right)\forall x \in \mathbb{R}$

• $f\left (x \right )=x\log x$ defined on $S=\left \{ x \in \mathbb{R}, x> 0 \right \}$.

  ${f}'x=1+\log x$

  ${f}''x=\frac{1}{x}>0$

  Thus, this function is strictly convex.

• $f \left (x \right )=e^{x},x \in \mathbb{R}$ is strictly convex.

Let $f:S \rightarrow \mathbb{R}$ where $S \subset \mathbb{R}^n$ is a non-empty convex set. The function f is said to be quasiconvex if for each $x_1,x_2 \in S$, we have $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq max\left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \},\lambda \in \left ( 0, 1 \right )$

For example, $f\left ( x \right )=x^{3}$

Let $f:S\rightarrow R $ where $S\subset \mathbb{R}^n$ is a non-empty convex set. The function f is said to be quasiconvex if for each $x_1, x_2 \in S$, we have $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\geq min\left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \}, \lambda \in \left ( 0, 1 \right )$

Remarks

• Every convex function is quasiconvex but the converse is not true.
• A function which is both quasiconvex and quasiconcave is called quasimonotone.

Theorem

Let $f:S\rightarrow \mathbb{R}$ and S is a non empty convex set in $\mathbb{R}^n$. The function f is quasiconvex if and only if $S_{\alpha} =\left ( x \in S:f\left ( x \right )\leq \alpha \right \}$ is convex for each real number \alpha$

Proof

Let f is quasiconvex on S.

Let $x_1,x_2 \in S_{\alpha}$ therefore $x_1,x_2 \in S$ and $max \left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \}\leq \alpha$

Let $\lambda \in \left (0, 1 \right )$ and let $x=\lambda x_1+\left ( 1-\lambda \right )x_2\leq max \left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \}\Rightarrow x \in S$

Thus, $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq max\left \{ f\left ( x_1 \right ), f\left ( x_2 \right ) \right \}\leq \alpha$

Therefore, $S_{\alpha}$ is convex.

Converse

Let $S_{\alpha}$ is convex for each $\alpha$

$x_1,x_2 \in S, \lambda \in \left ( 0,1\right )$

$x=\lambda x_1+\left ( 1-\lambda \right )x_2$

Let $x=\lambda x_1+\left ( 1-\lambda \right )x_2$

For $x_1, x_2 \in S_{\alpha}, \alpha= max \left \{ f\left ( x_1 \right ), f\left ( x_2 \right ) \right \}$

$\Rightarrow \lambda x_1+\left (1-\lambda \right )x_2 \in S_{\alpha}$

$\Rightarrow f \left (\lambda x_1+\left (1-\lambda \right )x_2 \right )\leq \alpha$

Hence proved.

Theorem

Let $f:S\rightarrow \mathbb{R}$ and S is a non empty convex set in $\mathbb{R}^n$. The function f is quasiconcave if and only if $S_{\alpha} =\left \{ x \in S:f\left ( x \right )\geq \alpha \right \}$ is convex for each real number $\alpha$.

Theorem

Let $f:S\rightarrow \mathbb{R}$ and S is a non empty convex set in $\mathbb{R}^n$. The function f is quasimonotone if and only if $S_{\alpha} =\left \{ x \in S:f\left ( x \right )= \alpha \right \}$ is convex for each real number $\alpha$.

Theorem

Let S be a non empty convex set in $\mathbb{R}^n$ and $f:S \rightarrow \mathbb{R}$ be differentiable on S, then f is quasiconvex if and only if for any $x_1,x_2 \in S$ and $f\left ( x_1 \right )\leq f\left ( x_2 \right )$, we have $\bigtriangledown f\left ( x_2 \right )^T\left ( x_2-x_1 \right )\leq 0$

Proof

Let f be a quasiconvex function.

Let $x_1,x_2 \in S$ such that $f\left ( x_1 \right ) \leq f\left ( x_2 \right )$

By differentiability of f at $x_2, \lambda \in \left ( 0, 1 \right )$

$f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )=f\left ( x_2+\lambda \left (x_1-x_2 \right ) \right )=f\left ( x_2 \right )+\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )$

$+\lambda \left \| x_1-x_2 \right \|\alpha \left ( x_2,\lambda \left ( x_1-x_2 \right ) \right )$

$\Rightarrow f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )-f\left ( x_2 \right )-f\left ( x_2 \right )=\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )$

$+\lambda \left \| x_1-x_2 \right \|\alpha \left ( x2, \lambda\left ( x_1-x_2 \right )\right )$

But since f is quasiconvex, $f \left ( \lambda x_1+ \left ( 1- \lambda \right )x_2 \right )\leq f \left (x_2 \right )$

$\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )+\lambda \left \| x_1-x_2 \right \|\alpha \left ( x_2,\lambda \left ( x_1,x_2 \right ) \right )\leq 0$

But $\alpha \left ( x_2,\lambda \left ( x_1,x_2 \right )\right )\rightarrow 0$ as $\lambda \rightarrow 0$

Therefore, $\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right ) \leq 0$

Converse

let for $x_1,x_2 \in S$ and $f\left ( x_1 \right )\leq f\left ( x_2 \right )$, $\bigtriangledown f\left ( x_2 \right )^T \left ( x_1,x_2 \right ) \leq 0$

To show that f is quasiconvex,ie, $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq f\left ( x_2 \right )$

Proof by contradiction

Suppose there exists an $x_3= \lambda x_1+\left ( 1-\lambda \right )x_2$ such that $f\left ( x_2 \right )< f \left ( x_3 \right )$ for some $ \lambda \in \left ( 0, 1 \right )$

For $x_2$ and $x_3,\bigtriangledown f\left ( x_3 \right )^T \left ( x_2-x_3 \right ) \leq 0$

$\Rightarrow -\lambda \bigtriangledown f\left ( x_3 \right )^T\left ( x_2-x_3 \right )\leq 0$

$\Rightarrow \bigtriangledown f\left ( x_3 \right )^T \left ( x_1-x_2 \right )\geq 0$

For $x_1$ and $x_3,\bigtriangledown f\left ( x_3 \right )^T \left ( x_1-x_3 \right ) \leq 0$

$\Rightarrow \left ( 1- \lambda \right )\bigtriangledown f\left ( x_3 \right )^T\left ( x_1-x_2 \right )\leq 0$

$\Rightarrow \bigtriangledown f\left ( x_3 \right )^T \left ( x_1-x_2 \right )\leq 0$

thus, from the above equations, $\bigtriangledown f\left ( x_3 \right )^T \left ( x_1-x_2 \right )=0$

Define $U=\left \{ x:f\left ( x \right )\leq f\left ( x_2 \right ),x=\mu x_2+\left ( 1-\mu \right )x_3, \mu \in \left ( 0,1 \right ) \right \}$

Thus we can find $x_0 \in U$ such that $x_0 = \mu_0 x_2= \mu x_2+\left ( 1- \mu \right )x_3$ for some $\mu _0 \in \left ( 0,1 \right )$ which is nearest to $x_3$ and $\hat{x} \in \left ( x_0,x_1 \right )$ such that by mean value theorem,

$$\frac{f\left ( x_3\right )-f\left ( x_0\right )}{x_3-x_0}= \bigtriangledown f\left ( \hat{x}\right )$$

$$\Rightarrow f\left ( x_3 \right )=f\left ( x_0 \right )+\bigtriangledown f\left ( \hat{x} \right )^T\left ( x_3-x_0 \right )$$

$$\Rightarrow f\left ( x_3 \right )=f\left ( x_0 \right )+\mu_0 \lambda f\left ( \hat{x}\right )^T \left ( x_1-x_2 \right )$$

Since $x_0$ is a combination of $x_1$ and $x_2$ and $f\left (x_2 \right )< f\left ( \hat{x}\right )$

By repeating the starting procedure, $\bigtriangledown f \left ( \hat{x}\right )^T \left ( x_1-x_2\right )=0$

Thus, combining the above equations, we get:

$$f\left ( x_3\right )=f\left ( x_0 \right ) \leq f\left ( x_2\right )$$

$$\Rightarrow f\left ( x_3\right )\leq f\left ( x_2\right )$$

Hence, it is contradiction.

Examples

Step 1 − $f\left ( x\right )=X^3$

$Let f \left ( x_1\right )\leq f\left ( x_2\right )$

$\Rightarrow x_{1}^{3}\leq x_{2}^{3}\Rightarrow x_1\leq x_2$

$\bigtriangledown f\left ( x_2 \right )\left ( x_1-x_2 \right )=3x_{2}^{2}\left ( x_1-x_2 \right )\leq 0$

Thus, $f\left ( x\right )$ is quasiconvex.

Step 2 − $f\left ( x\right )=x_{1}^{3}+x_{2}^{3}$

Let $\hat{x_1}=\left ( 2, -2\right )$ and $\hat{x_2}=\left ( 1, 0\right )$

thus, $f\left ( \hat{x_1}\right )=0,f\left ( \hat{x_2}\right )=1 \Rightarrow f\left ( \hat{x_1}\right )\setminus < f \left ( \hat{x_2}\right )$

Thus, $\bigtriangledown f \left ( \hat{x_2}\right )^T \left ( \hat{x_1}- \hat{x_2}\right )= \left ( 3, 0\right )^T \left ( 1, -2\right )=3 >0$

Hence $f\left ( x\right )$ is not quasiconvex.

Let $f:S\rightarrow \mathbb{R}^n$ and S be a non-empty convex set in $\mathbb{R}^n$ then f is said to be strictly quasicovex function if for each $x_1,x_2 \in S$ with $f\left ( x_1 \right ) \neq f\left ( x_2 \right )$, we have $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )< max \:\left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \}$

Remarks

• Every strictly quasiconvex function is strictly convex.
• Strictly quasiconvex function does not imply quasiconvexity.
• Strictly quasiconvex function may not be strongly quasiconvex.
• Pseudoconvex function is a strictly quasiconvex function.

Theorem

Let $f:S\rightarrow \mathbb{R}^n$ be strictly quasiconvex function and S be a non-empty convex set in $\mathbb{R}^n$.Consider the problem: $min \:f\left ( x \right ), x \in S$. If $\hat{x}$ is local optimal solution, then $\bar{x}$ is global optimal solution.

Proof

Let there exists $ \bar{x} \in S$ such that $f\left ( \bar{x}\right )\leq f \left ( \hat{x}\right )$

Since $\bar{x},\hat{x} \in S$ and S is convex set, therefore,

$$\lambda \bar{x}+\left ( 1-\lambda \right )\hat{x}\in S, \forall \lambda \in \left ( 0,1 \right )$$

Since $\hat{x}$ is local minima, $f\left ( \hat{x} \right ) \leq f\left ( \lambda \bar{x}+\left ( 1-\lambda \right )\hat{x} \right ), \forall \lambda \in \left ( 0,\delta \right )$

Since f is strictly quasiconvex.

$$f\left ( \lambda \bar{x}+\left ( 1-\lambda \right )\hat{x} \right )< max \left \{ f\left ( \hat{x} \right ),f\left ( \bar{x} \right ) \right \}=f\left ( \hat{x} \right )$$

Hence, it is contradiction.

Strictly quasiconcave function

Let $f:S\rightarrow \mathbb{R}^n$ and S be a non-empty convex set in $\mathbb{R}^n$, then f is saud to be strictly quasicovex function if for each $x_1,x_2 \in S$ with $f\left (x_1\right )\neq f\left (x_2\right )$, we have

$$f\left (\lambda x_1+\left (1-\lambda\right )x_2\right )> min \left \{ f \left (x_1\right ),f\left (x_2\right )\right \}$$.

Examples

• $f\left (x\right )=x^2-2$

  It is a strictly quasiconvex function because if we take any two points $x_1,x_2$ in the domain that satisfy the constraints in the definition $f\left (\lambda x_1+\left (1- \lambda\right )x_2\right )< max \left \{ f \left (x_1\right ),f\left (x_2\right )\right \}$ As the function is decreasing in the negative x-axis and it is increasing in the positive x-axis (since it is a parabola).

• $f\left (x\right )=-x^2$

  It is not a strictly quasiconvex function because if we take take $x_1=1$ and $x_2=-1$ and $\lambda=0.5$, then $f\left (x_1\right )=-1=f\left (x_2\right )$ but $f\left (\lambda x_1+\left (1- \lambda\right )x_2\right )=0$ Therefore it does not satisfy the conditions stated in the definition. But it is a quasiconcave function because if we take any two points in the domain that satisfy the constraints in the definition $f\left ( \lambda x_1+\left (1-\lambda\right )x_2\right )> min \left \{ f \left (x_1\right ),f\left (x_2\right )\right \}$. As the function is increasing in the negative x-axis and it is decreasing in the positive x-axis.

Let $f:S\rightarrow \mathbb{R}^n$ and S be a non-empty convex set in $\mathbb{R}^n$ then f is strongly quasiconvex function if for any $x_1,x_2 \in S$ with $\left ( x_1 \right ) \neq \left ( x_2 \right )$, we have $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )< max \:\left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \},\forall \lambda \in \left ( 0,1\right )$

Theorem

A quasiconvex function $f:S\rightarrow \mathbb{R}^n$ on a non-empty convex set S in $\mathbb{R}^n$ is strongly quasiconvex function if it is not constant on a line segment joining any points of S.

Proof

Let f is quasiconvex function and it is not constant on a line segment joining any points of S.

Suppose f is not strongly quasiconvex function.

There exist $x_1,x_2 \in S$ with $x_1 \neq x_2$ such that

$$f\left ( z \right )\geq max\left \{ f\left ( x_1 \right ), f\left ( x_2 \right ) \right \}, \forall z= \lambda x_1+\left ( 1-\lambda \right )x_2, \lambda \in \left ( 0,1 \right )$$

$\Rightarrow f\left ( x_1 \right )\leq f\left ( z \right )$ and $f\left ( x_2 \right )\leq f\left ( z \right )$

Since f is not constant in $\left [ x_1,z \right ]$ and $\left [z,x_2 \right ] $

So there exists $u \in \left [ x_1,z \right ]$ and $v=\left [ z,x_2 \right ]$

$$\Rightarrow u= \mu_1x_1+\left ( 1-\mu_1\right )z,v=\mu_2z+\left ( 1- \mu_2\right )x_2$$

Since f is quasiconvex,

$$\Rightarrow f\left ( u \right )\leq max\left \{ f\left ( x_1 \right ),f \left ( z \right ) \right \}=f\left ( z \right )\:\: and \:\:f \left ( v \right ) \leq max \left \{ f\left ( z \right ),f\left ( x_2 \right ) \right \}$$

$$\Rightarrow f\left ( u \right )\leq f\left ( z \right ) \:\: and \:\: f\left ( v \right )\leq f\left ( z \right )$$

$$\Rightarrow max \left \{ f\left ( u \right ),f\left ( v \right ) \right \} \leq f\left ( z \right )$$

But z is any point between u and v, if any of them are equal, then f is constant.

Therefore, $max \left \{ f\left ( u \right ),f\left ( v \right ) \right \} \leq f\left ( z \right )$

which contradicts the quasiconvexity of f as $z \in \left [ u,v \right ]$.

Hence f is strongly quasiconvex function.

Theorem

Let $f:S\rightarrow \mathbb{R}^n$ and S be a non-empty convex set in $\mathbb{R}^n$. If $\hat{x}$ is local optimal solution, then $\hat{x}$ is unique global optimal solution.

Proof

Since a strong quasiconvex function is also strictly quasiconvex function, thus a local optimal solution is global optimal solution.

Uniqueness − Let f attains global optimal solution at two points $u,v \in S$

$$\Rightarrow f\left ( u \right ) \leq f\left ( x \right ).\forall x \in S\:\: and \:\:f\left ( v \right ) \leq f\left ( x \right ).\forall x \in S$$

If u is global optimal solution, $f\left ( u \right )\leq f\left ( v \right )$ and $f\left ( v \right )\leq f\left ( u\right )\Rightarrow f\left ( u \right )=f\left ( v\right )$

$$f\left ( \lambda u+\left ( 1-\lambda\right )v\right )< max \left \{f\left ( u \right ),f\left ( v \right ) \right \}=f\left ( u \right )$$

which is a contradiction.

Hence there exists only one global optimal solution.

Remarks

• A strongly quasiconvex function is also strictly quasiconvex fucntion.
• A strictly convex function may or may not be strongly quasiconvex.
• A differentiable strictly convex is strongly quasiconvex.

Let $f:S\rightarrow \mathbb{R}$ be a differentiable function and S be a non-empty convex set in $\mathbb{R}^n$, then f is said to be pseudoconvex if for each $x_1,x_2 \in S$ with $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\geq 0$, we have $f\left ( x_2 \right )\geq f\left ( x_1 \right )$, or equivalently if $f\left ( x_1 \right )>f\left ( x_2 \right )$ then $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )<0$

Pseudoconcave function

Let $f:S\rightarrow \mathbb{R}$ be a differentiable function and S be a non-empty convex set in $\mathbb{R}^n$, then f is said to be pseudoconvex if for each $x_1, x_2 \in S$ with $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\geq 0$, we have $f\left ( x_2 \right )\leq f\left ( x_1 \right )$, or equivalently if $f\left ( x_1 \right )>f\left ( x_2 \right )$ then $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )>0$

Remarks

• If a function is both pseudoconvex and pseudoconcave, then is is called pseudolinear.

• A differentiable convex function is also pseudoconvex.

• A pseudoconvex function may not be convex. For example,

  $f\left ( x \right )=x+x^3$ is not convex. If $x_1 \leq x_2,x_{1}^{3} \leq x_{2}^{3}$

  Thus,$\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )=\left ( 1+3x_{1}^{2} \right )\left ( x_2-x_1 \right ) \geq 0$

  And, $f\left ( x_2 \right )-f\left ( x_1 \right )=\left ( x_2-x_1 \right )+\left ( x_{2}^{3} -x_{1}^{3}\right )\geq 0$

  $\Rightarrow f\left ( x_2 \right )\geq f\left ( x_1 \right )$

  Thus, it is pseudoconvex.

  A pseudoconvex function is strictly quasiconvex. Thus, every local minima of pseudoconvex is also global minima.

Strictly pseudoconvex function

Let $f:S\rightarrow \mathbb{R}$ be a differentiable function and S be a non-empty convex set in $\mathbb{R}^n$, then f is said to be pseudoconvex if for each $x_1,x_2 \in S$ with $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\geq 0$, we have $f\left ( x_2 \right )> f\left ( x_1 \right )$,or equivalently if $f\left ( x_1 \right )\geq f\left ( x_2 \right )$ then $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )<0$

Theorem

Let f be a pseudoconvex function and suppose $\bigtriangledown f\left ( \hat{x}\right )=0$ for some $\hat{x} \in S$, then $\hat{x}$ is global optimal solution of f over S.

Proof

Let $\hat{x}$ be a critical point of f, ie, $\bigtriangledown f\left ( \hat{x}\right )=0$

Since f is pseudoconvex function, for $x \in S,$ we have

$$\bigtriangledown f\left ( \hat{x}\right )\left ( x-\hat{x}\right )=0 \Rightarrow f\left ( \hat{x}\right )\leq f\left ( x\right ), \forall x \in S$$

Hence, $\hat{x}$ is global optimal solution.

Remark

If f is strictly pseudoconvex function, $\hat{x}$ is unique global optimal solution.

Theorem

If f is differentiable pseudoconvex function over S, then f is both strictly quasiconvex as well as quasiconvex function.

Remarks

• The sum of two pseudoconvex fucntions defined on an open set S of $\mathbb{R}^n$ may not be pseudoconvex.

• Let $f:S\rightarrow \mathbb{R}$ be a quasiconvex function and S be a non-empty convex subset of $\mathbb{R}^n$ then f is pseudoconvex if and only if every critical point is a global minima of f over S.

• Let S be a non-empty convex subset of $\mathbb{R}^n$ and $f:S\rightarrow \mathbb{R}$ be a function such that $\bigtriangledown f\left ( x\right )\neq 0$ for every $x \in S$ then f is pseudoconvex if and only if it is a quasiconvex function.

There are four types of convex programming problems −

Step 1 − $min \:f\left ( x \right )$, where $x \in S$ and S be a non-empty convex set in $\mathbb{R}^n$ and $f\left ( x \right )$ is convex function.

Step 2 − $min \: f\left ( x \right ), x \in \mathbb{R}^n$ subject to

$g_i\left ( x \right ) \geq 0, 1 \leq m_1$ and $g_i\left ( x \right )$ is a convex function.

$g_i\left ( x \right ) \leq 0,m_1+1 \leq m_2$ and $g_i\left ( x \right )$ is a concave function.

$g_i\left ( x \right ) = 0, m_2+1 \leq m$ and $g_i\left ( x \right )$ is a linear function.

where $f\left ( x \right )$ is a convex fucntion.

Step 3 − $max \:f\left ( x \right )$ where $x \in S$ and S be a non-empty convex set in $\mathbb{R}^n$ and $f\left ( x \right )$ is concave function.

Step 4 − $min \:f\left ( x \right )$, where $x \in \mathbb{R}^n$ subject to

$g_i\left ( x \right ) \geq 0, 1 \leq m_1$ and $g_i\left ( x \right )$ is a convex function.

$g_i\left ( x \right ) \leq 0, m_1+1 \leq m_2$ and $g_i\left ( x \right )$ is a concave function.

$g_i\left ( x \right ) = 0,m_2+1 \leq m$ and $g_i\left ( x \right )$ is a linear function.

where $f\left ( x \right )$ is a concave function.

Cone of feasible direction

Let S be a non-empty set in $\mathbb{R}^n$ and let $\hat{x} \in \:Closure\left ( S \right )$, then the cone of feasible direction of S at $\hat{x}$, denoted by D, is defined as $D=\left \{ d:d\neq 0,\hat{x}+\lambda d \in S, \lambda \in \left ( 0, \delta \right ), \delta > 0 \right \}$

Each non-zero vector $d \in D$ is called feasible direction.

For a given function $f:\mathbb{R}^n \Rightarrow \mathbb{R}$ the cone of improving direction at $\hat{x}$ is denoted by F and is given by

$$F=\left \{ d:f\left ( \hat{x}+\lambda d \right )\leq f\left ( \hat{x} \right ),\forall \lambda \in \left ( 0,\delta \right ), \delta >0 \right \}$$

Each direction $d \in F$ is called an improving direction or descent direction of f at $\hat{x}$

Theorem

Necessary Condition

Consider the problem $min f\left ( x \right )$ such that $x \in S$ where S be a non-empty set in $\mathbb{R}^n$. Suppose f is differentiable at a point $\hat{x} \in S$. If $\hat{x}$ is a local optimal solution, then $F_0 \cap D= \phi$ where $F_0=\left \{ d:\bigtriangledown f\left ( \hat{x} \right )^T d < 0 \right \}$ and D is a cone of feasible direction.

Sufficient Condition

If $F_0 \cap D= \phi$ f is a pseudoconvex function at $\hat{x}$ and there exists a neighbourhood of $\hat{x},N_\varepsilon \left ( \hat{x} \right ), \varepsilon > 0$ such that $d=x-\hat{x}\in D$ for any $x \in S \cap N_\varepsilon \left ( \hat{x} \right )$, then $\hat{x}$ is local optimal solution.

Proof

Necessary Condition

Let $F_0 \cap D\neq \phi$, ie, there exists a $d \in F_0 \cap D$ such that $d \in F_0$ and $d\in D$

Since $d \in D$, therefore there exists $\delta_1 >0$ such that $\hat{x}+\lambda d \in S, \lambda \in \left ( 0,\delta_1 \right ).$

Since $d \in F_0$, therefore $\bigtriangledown f \left ( \hat{x}\right )^T d <0$

Thus, there exists $\delta_2>0$ such that $f\left ( \hat{x}+\lambda d\right )< f\left ( \hat{x}\right ),\forall \lambda \in f \left ( 0,\delta_2 \right )$

Let $\delta=min \left \{\delta_1,\delta_2 \right \}$

Then $\hat{x}+\lambda d \in S, f\left (\hat{x}+\lambda d \right ) < f\left ( \hat{x} \right ),\forall \lambda \in f \left ( 0,\delta \right )$

But $\hat{x}$ is local optimal solution.

Hence it is contradiction.

Thus $F_0\cap D=\phi$

Sufficient Condition

Let $F_0 \cap D\neq \phi$ nd let f be a pseudoconvex function.

Let there exists a neighbourhood of $\hat{x}, N_{\varepsilon}\left ( \hat{x} \right )$ such that $d=x-\hat{x}, \forall x \in S \cap N_\varepsilon\left ( \hat{x} \right )$

Let $\hat{x}$ is not a local optimal solution.

Thus, there exists $\bar{x} \in S \cap N_\varepsilon \left ( \hat{x} \right )$ such that $f \left ( \bar{x} \right )< f \left ( \hat{x} \right )$

By assumption on $S \cap N_\varepsilon \left ( \hat{x} \right ),d=\left ( \bar{x}-\hat{x} \right )\in D$

By pseudoconvex of f,

$$f\left ( \hat{x} \right )>f\left ( \bar{x} \right )\Rightarrow \bigtriangledown f\left ( \hat{x} \right )^T\left ( \bar{x}-\hat{x} \right )<0$$

$\Rightarrow \bigtriangledown f\left ( \hat{x} \right) ^T d <0$

$\Rightarrow d \in F_0$

hence $F_0\cap D \neq \phi$

which is a contradiction.

Hence, $\hat{x}$ is local optimal solution.

Consider the following problem:$min \:f\left ( x\right )$ where $x \in X$ such that $g_x\left ( x\right ) \leq 0, i=1,2,...,m$

$f:X \rightarrow \mathbb{R},g_i:X \rightarrow \mathbb{R}^n$ and X is an open set in $\mathbb{R}^n$

Let $S=\left \{x:g_i\left ( x\right )\leq 0,\forall i \right \}$

Let $\hat{x} \in X$, then $M=\left \{1,2,...,m \right \}$

Let $I=\left \{i:g_i\left ( \hat{x}\right )=0, i \in M\right \}$ where I is called index set for all active constraints at $\hat{x}$

Let $J=\left \{i:g_i\left ( \hat{x}\right )<0,i \in M\right \}$ where J is called index set for all active constraints at $\hat{x}$.

Let $F_0=\left \{ d \in \mathbb{R}^m:\bigtriangledown f\left ( \hat{x} \right )^T d <0 \right \}$

Let $G_0=\left \{ d \in \mathbb{R}^m:\bigtriangledown gI\left ( \hat{x} \right )^T d <0 \right \}$

or $G_0=\left \{ d \in \mathbb{R}^m:\bigtriangledown gi\left ( \hat{x} \right )^T d <0 ,\forall i \in I \right \}$

Lemma

If $S=\left \{ x \in X:g_i\left ( x\right ) \leq 0, \forall i \in I\right \}$ and X is non-empty open set in $\mathbb{R}^n$. Let $\hat{x}\in S$ and $g_i$ are different at $\hat{x}, i \in I$ and let $g_i$ where $i \in J$ are continuous at $\hat{x}$, then $G_0 \subseteq D$.

Proof

Let $d \in G_0$

Since $\hat{x} \in X$ and X is an open set, thus there exists $\delta_1 >0$ such that $\hat{x}+\lambda d \in X$ for $\lambda \in \left ( 0, \delta_1\right )$

Also since $g_\hat{x}<0$ and $g_i$ are continuous at $\hat{x}, \forall i \in J$, there exists $\delta_2>0$, $g_i\left ( \hat{x}+\lambda d\right )<0, \lambda \in \left ( 0, \delta_2\right )$

Since $d \in G_0$, therefore, $\bigtriangledown g_i\left ( \hat{x}\right )^T d <0, \forall i \in I$ thus there exists $\delta_3 >0, g_i\left ( \hat{x}+\lambda d\right )< g_i\left ( \hat{x}\right )=0$, for $\lambda \in \left ( 0, \delta_3\right ) i \in J$

Let $\delta=min\left \{ \delta_1, \delta_2, \delta_3 \right \}$

therefore, $\hat{x}+\lambda d \in X, g_i\left ( \hat{x}+\lambda d\right )< 0, i \in M$

$\Rightarrow \hat{x}+\lambda d \in S$

$\Rightarrow d \in D$

$\Rightarrow G_0 \subseteq D$

Hence Proved.

Theorem

Necessary Condition

Let $f$ and $g_i, i \in I$, are different at $\hat{x} \in S,$ and $g_j$ are continous at $\hat{x} \in S$. If $\hat{x}$ is local minima of $S$, then $F_0 \cap G_0=\phi$.

Sufficient Condition

If $F_0 \cap G_0= \phi$ and f is a pseudoconvex function at $\left (\hat{x}, g_i 9x \right ), i \in I$ are strictly pseudoconvex functions over some $\varepsilon$ - neighbourhood of $\hat{x}, \hat{x}$ is a local optimal solution.

Bemerkungen

• Sei $ \ hat {x} $ ein machbarer Punkt, so dass $ \ bigtriangledown f \ left (\ hat {x} \ right) = 0 $, dann $ F_0 = \ phi $. Somit ist $ F_0 \ cap G_0 = \ phi $, aber $ \ hat {x} $ ist keine optimale Lösung

• Aber wenn $ \ bigtriangledown g \ left (\ hat {x} \ right) = 0 $ ist, dann ist $ G_0 = \ phi $, also $ F_0 \ cap G_0 = \ phi $

• Betrachten Sie das Problem: min $ f \ left (x \ right) $, so dass $ g \ left (x \ right) = 0 $.

  Da $ g \ left (x \ right) = 0 $ ist, ist $ g_1 \ left (x \ right) = g \ left (x \ right) <0 $ und $ g_2 \ left (x \ right) = - g \ left (x \ right) \ leq 0 $.

  Sei $ \ hat {x} \ in S $, dann $ g_1 \ left (\ hat {x} \ right) = 0 $ und $ g_2 \ left (\ hat {x} \ right) = 0 $.

  Aber $ \ bigtriangledown g_1 \ left (\ hat {x} \ right) = - \ bigtriangledown g_2 \ left (\ hat {x} \ right) $

  Somit ist $ G_0 = \ phi $ und $ F_0 \ cap G_0 = \ phi $.

Notwendige Bedingungen

Satz

Betrachten Sie das Problem - $ min f \ left (x \ right) $, so dass $ x \ in X $ wobei X eine offene Menge in $ \ mathbb {R} ^ n $ ist, und lassen Sie $ g_i \ left (x \ right) \ leq 0, \ forall i = 1,2, .... m $.

Sei $ f: X \ rightarrow \ mathbb {R} $ und $ g_i: X \ rightarrow \ mathbb {R} $

Sei $ \ hat {x} $ eine praktikable Lösung und sei f und $ g_i, i \ in I $ sind differenzierbar bei $ \ hat {x} $ und $ g_i, i \ in J $ sind stetig bei $ \ hat { x} $.

Wenn $ \ hat {x} $ das obige Problem lokal löst, gibt es $ u_0, u_i \ in \ mathbb {R}, i \ in I $, so dass $ u_0 \ bigtriangledown f \ left (\ hat {x} \ rechts) + \ displaystyle \ sum \ limit_ {i \ in I} u_i \ bigtriangledown g_i \ left (\ hat {x} \ right) $ = 0

Dabei ist $ u_0, u_i \ geq 0, i \ in I $ und $ \ left (u_0, u_I \ right) \ neq \ left (0,0 \ right) $

Wenn $ g_i, i \ in J $ auch bei $ \ hat {x} $ differenzierbar sind, können die obigen Bedingungen wie folgt geschrieben werden:

$ u_0 \ bigtriangledown f \ left (\ hat {x} \ right) + \ displaystyle \ sum \ limit_ {i = 1} ^ m u_i \ bigtriangledown g_i \ left (\ hat {x} \ right) = 0 $

$ u_ig_i \ left (\ hat {x} \ right) $ = 0

$ u_0, u_i \ geq 0, \ forall i = 1,2, ...., m $

$ \ left (u_0, u \ right) \ neq \ left (0,0 \ right), u = \ left (u_1, u_2, s, u_m \ right) \ in \ mathbb {R} ^ m $

Bemerkungen

• $ u_i $ heißen Lagrange-Multiplikatoren.

• Die Bedingung, dass $ \ hat {x} $ für das gegebene Problem realisierbar ist, wird als primär realisierbare Bedingung bezeichnet.

• Die Anforderung $ u_0 \ bigtriangledown f \ left (\ hat {x} \ right) + \ displaystyle \ sum \ limit_ {i = 1} ^ m ui \ bigtriangledown g_i \ left (x \ right) = 0 $ wird als doppelte Machbarkeit bezeichnet Bedingung.

• Die Bedingung $ u_ig_i \ left (\ hat {x} \ right) = 0, i = 1, 2, ... m $ wird als komplementäre Schlaffheitsbedingung bezeichnet. Diese Bedingung erfordert $ u_i = 0, i \ in J $

• Zusammen werden die ursprüngliche Durchführbarkeitsbedingung, die doppelte Durchführbarkeitsbedingung und die komplementäre Schlaffheit als Fritz-John-Bedingungen bezeichnet.

Ausreichende Bedingungen

Satz

Wenn es eine $ \ varepsilon $ -Nachbarschaft von $ \ hat {x} N_ \ varepsilon \ left (\ hat {x} \ right) gibt, \ varepsilon> 0 $, so dass f pseudokonvex über $ N_ \ varepsilon \ left ist ( \ hat {x} \ right) \ cap S $ und $ g_i, i \ in I $ sind streng pseudokonvex über $ N_ \ varepsilon \ left (\ hat {x} \ right) \ cap S $, dann $ \ hat { x} $ ist eine lokal optimale Lösung für das oben beschriebene Problem. Wenn f bei $ \ hat {x} $ pseudokonvex ist und wenn $ g_i, i \ in I $ bei $ \ hat {x} sowohl streng pseudokonvex als auch quasikonvex sind, ist \ hat {x} $ eine globale optimale Lösung für das Problem oben beschrieben.

Beispiel

• $ min \: f \ left (x_1, x_2 \ right) = \ left (x_1-3 \ right) ^ 2 + \ left (x_2-2 \ right) ^ 2 $

  so dass $ x_ {1} ^ {2} + x_ {2} ^ {2} \ leq 5, x_1 + 2x_2 \ leq 4, x_1, x_2 \ geq 0 $ und $ \ hat {x} = \ left (2 , 1 \ rechts) $

  Sei $ g_1 \ left (x_1, x_2 \ right) = x_ {1} ^ {2} + x_ {2} ^ {2} -5, $

  $ g_2 \ left (x_1, x_2 \ right) = x_1 + 2x_2-4, $

  $ g_3 \ left (x_1, x_2 \ right) = - x_1 $ und $ g_4 \ left (x_1, x_2 \ right) = -x_2 $.

  Somit können die obigen Einschränkungen wie folgt geschrieben werden:

  $ g_1 \ left (x_1, x_2 \ right) \ leq 0, $

  $ g_2 \ left (x_1, x_2 \ right) \ leq 0, $

  $ g_3 \ left (x_1, x_2 \ right) \ leq 0 $ und

  $ g_4 \ left (x_1, x_2 \ right) \ leq 0 $ Somit ist $ I = \ left \ {1,2 \ right \} $, also $ u_3 = 0, u_4 = 0 $

  $ \ bigtriangledown f \ left (\ hat {x} \ right) = \ left (2, -2 \ right), \ bigtriangledown g_1 \ left (\ hat {x} \ right) = \ left (4,2 \ right) ) $ und $ \ bigtriangledown g_2 \ left (\ hat {x} \ right) = \ left (1,2 \ right) $

  Wenn wir diese Werte in die erste Bedingung der Fritz-John-Bedingungen setzen, erhalten wir -

  $ u_0 = \ frac {3} {2} u_2, \: \: u_1 = \ frac {1} {2} u_2, $ und lassen Sie $ u_2 = 1 $, daher $ u_0 = \ frac {3} {2} , \: \: u_1 = \ frac {1} {2} $

  Damit sind die Bedingungen von Fritz John erfüllt.

• $ min f \ left (x_1, x_2 \ right) = - x_1 $.

  so dass $ x_2- \ left (1-x_1 \ right) ^ 3 \ leq 0 $,

  $ -x_2 \ leq 0 $ und $ \ hat {x} = \ left (1,0 \ right) $

  Sei $ g_1 \ left (x_1, x_2 \ right) = x_2- \ left (1-x_1 \ right) ^ 3 $,

  $ g_2 \ left (x_1, x_2 \ right) = - x_2 $

  Somit können die obigen Einschränkungen wie folgt geschrieben werden:

  $ g_1 \ left (x_1, x_2 \ right) \ leq 0, $

  $ g_2 \ left (x_1, x_2 \ right) \ leq 0, $

  Somit ist $ I = \ left \ {1,2 \ right \} $

  $ \ bigtriangledown f \ left (\ hat {x} \ right) = \ left (-1,0 \ right) $

  $ \ bigtriangledown g_1 \ left (\ hat {x} \ right) = \ left (0,1 \ right) $ und $ g_2 \ left (\ hat {x} \ right) = \ left (0, -1 \ right) ) $

  Wenn wir diese Werte in die erste Bedingung der Fritz-John-Bedingungen setzen, erhalten wir -

  $ u_0 = 0, \: \: u_1 = u_2 = a> 0 $

  Damit sind die Bedingungen von Fritz John erfüllt.

Betrachten Sie das Problem -

$ min \: f \ left (x \ right) $, so dass $ x \ in X $, wobei X eine offene Menge in $ \ mathbb {R} ^ n $ und $ g_i \ left (x \ right) \ leq ist 0, i = 1, 2, ..., m $

Sei $ S = \ left \ {x \ in X: g_i \ left (x \ right) \ leq 0, \ forall i \ right \} $

Sei $ \ hat {x} \ in S $ und sei $ f $ und $ g_i, i \ in I $ differenzierbar bei $ \ hat {x} $ und $ g_i, i \ in J $ sind stetig bei $ \ hat {x} $. Außerdem sind $ \ bigtriangledown g_i \ left (\ hat {x} \ right), i \ in I $ linear unabhängig. Wenn $ \ hat {x} $ das obige Problem lokal löst, existiert $ u_i, i \ in I $, so dass

$ \ bigtriangledown f \ left (x \ right) + \ displaystyle \ sum \ limit_ {i \ in I} u_i \ bigtriangledown g_i \ left (\ hat {x} \ right) = 0 $, $ \: \: u_i \ geq 0, i \ in I $

Wenn $ g_i, sind i \ in J $ auch bei $ \ hat {x} $ differenzierbar. dann $ \ hat {x} $, dann

$ \ bigtriangledown f \ left (\ hat {x} \ right) + \ displaystyle \ sum \ limit_ {i = 1} ^ m u_i \ bigtriangledown g_i \ left (\ hat {x} \ right) = 0 $

$ u_ig_i \ left (\ hat {x} \ right) = 0, \ forall i = 1,2, ..., m $

$ u_i \ geq 0 \ forall i = 1,2, ..., m $

Beispiel

Betrachten Sie das folgende Problem -

$ min \: f \ left (x_1, x_2 \ right) = \ left (x_1-3 \ right) ^ 2 + \ left (x_2-2 \ right) ^ 2 $

so dass $ x_ {1} ^ {2} + x_ {2} ^ {2} \ leq 5 $,

$ x_1,2x_2 \ geq 0 $ und $ \ hat {x} = \ left (2,1 \ right) $

Sei $ g_1 \ left (x_1, x_2 \ right) = x_ {1} ^ {2} + x_ {2} ^ {2} -5 $,

$ g_2 \ left (x_1, x_2 \ right) = x_ {1} + 2x_2-4 $

$ g_3 \ left (x_1, x_2 \ right) = - x_ {1} $ und $ g_4 \ left (x_1, x_2 \ right) = - x_2 $

Somit können die obigen Einschränkungen wie folgt geschrieben werden:

$ g_1 \ left (x_1, x_2 \ right) \ leq 0, g_2 \ left (x_1, x_2 \ right) \ leq 0 $

$ g_3 \ left (x_1, x_2 \ right) \ leq 0, $ und $ g_4 \ left (x_1, x_2 \ right) \ leq 0 $ Somit ist $ I = \ left \ {1,2 \ right \} $ , $ u_3 = 0, \: \: u_4 = 0 $

$ \ bigtriangledown f \ left (\ hat {x} \ right) = \ left (2, -2 \ right), \ bigtriangledown g_1 \ left (\ hat {x} \ right) = \ left (4,2 \ right) ) $ und

$ \ bigtriangledown g_2 \ left (\ hat {x} \ right) = \ left (1,2 \ right) $

Wenn wir diese Werte in die erste Bedingung der Karush-Kuhn-Tucker-Bedingungen setzen, erhalten wir -

$ u_1 = \ frac {1} {3} $ und $ u_2 = \ frac {2} {3} $

Damit sind die Karush-Kuhn-Tucker-Bedingungen erfüllt.

Methode des steilsten Abstiegs

Diese Methode wird auch als Gradientenmethode oder Cauchy's-Methode bezeichnet. Diese Methode umfasst die folgenden Terminologien:

$$ x_ {k + 1} = x_k + \ alpha_kd_k $$

$ d_k = - \ bigtriangledown f \ left (x_k \ right) $ oder $ d_k = - \ frac {\ bigtriangledown f \ left (x_k \ right)} {\ left \ | \ bigtriangledown f \ left (x_k \ right) \ right \ |} $

Sei $ \ phi \ left (\ alpha \ right) = f \ left (x_k + \ alpha d_k \ right) $

Durch Differenzieren von $ \ phi $ und Gleichsetzen mit Null können wir $ \ alpha $ erhalten.

Der Algorithmus lautet also wie folgt:

• Initialisieren Sie $ x_0 $, $ \ varepsilon_1 $, $ \ varepsilon_2 $ und setzen Sie $ k = 0 $.

• Setze $ d_k = - \ bigtriangledown f \ left (x_k \ right) $ oder $ d_k = - \ frac {\ bigtriangledown f \ left (x_k \ right)} {\ left \ | \ bigtriangledown f \ left (x_k \ right) \ right \ |} $.

• finde $ \ alpha_k $ so, dass $ \ phi \ left (\ alpha \ right) = f \ left (x_k + \ alpha d_k \ right) $ minimiert wird.

• Setze $ x_ {k + 1} = x_k + \ alpha_kd_k $.

• Wenn $ \ left \ | x_ {k + 1-x_k} \ right \ | <\ varepsilon_1 $ oder $ \ left \ | \ bigtriangledown f \ left (x_ {k + 1} \ right) \ right \ | \ leq \ varepsilon_2 $, gehe zu Schritt 6, andernfalls setze $ k = k + 1 $ und gehe zu Schritt 2.

• Die optimale Lösung ist $ \ hat {x} = x_ {k + 1} $.

Newton-Methode

Die Newton-Methode arbeitet nach folgendem Prinzip:

$ f \ left (x \ right) = y \ left (x \ right) = f \ left (x_k \ right) + \ left (x-x_k \ right) ^ T \ bigtriangledown f \ left (x_k \ right) + \ frac {1} {2} \ left (x-x_k \ right) ^ TH \ left (x_k \ right) \ left (x-x_k \ right) $

$ \ bigtriangledown y \ left (x \ right) = \ bigtriangledown f \ left (x_k \ right) + H \ left (x_k \ right) \ left (x-x_k \ right) $

Bei $ x_ {k + 1} ist \ bigtriangledown y \ left (x_ {k + 1} \ right) = \ bigtriangledown f \ left (x_k \ right) + H \ left (x_k \ right) \ left (x_ {k +1} -x_k \ right) $

Damit $ x_ {k + 1} $ die optimale Lösung ist $ \ bigtriangledown y \ left (x_k + 1 \ right) = 0 $

Somit ist $ x_ {k + 1} = x_k-H \ left (x_k \ right) ^ {- 1} \ bigtriangledown f \ left (x_k \ right) $

Hier sollte $ H \ left (x_k \ right) $ nicht singulär sein.

Daher lautet der Algorithmus wie folgt:

Step 1 - Initialisieren Sie $ x_0, \ varepsilon $ und setzen Sie $ k = 0 $.

Step 2 - finde $ H \ left (x_k \ right) \ bigtriangledown f \ left (x_k \ right) $.

Step 3 - Löse nach dem linearen System $ H \ left (x_k \ right) h \ left (x_k \ right) = \ bigtriangledown f \ left (x_k \ right) $ für $ h \ left (x_k \ right) $.

Step 4 - finde $ x_ {k + 1} = x_k-h \ left (x_k \ right) $.

Step 5- Wenn $ \ left \ | x_ {k + 1} -x_k \ right \ | <\ varepsilon $ oder $ \ left \ | \ bigtriangledown f \ left (x_k \ right) \ right \ | \ leq \ varepsilon $ dann gehe zu Schritt 6, sonst setze $ k = k + 1 $ und gehe zu Schritt 2.

Step 6 - Die optimale Lösung ist $ \ hat {x} = x_ {k + 1} $.

Gradientenmethode konjugieren

Diese Methode wird zur Lösung der folgenden Probleme verwendet:

$ min f \ left (x \ right) = \ frac {1} {2} x ^ T Qx-bx $

wobei Q eine positiv definierte nXn-Matrix ist und b konstant ist.

Wenn $ x_0, \ varepsilon gegeben ist, berechnet $ $ g_0 = Qx_0-b $

Setze $ d_0 = -g_0 $ für $ k = 0,1,2, ..., $

Setze $ \ alpha_k = \ frac {g_ {k} ^ {T} g_k} {d_ {k} ^ {T} Q d_k} $

Berechnen Sie $ x_ {k + 1} = x_k + \ alpha_kd_k $

Setze $ g_ {k + 1} = g_k + \ alpha_kd_k $

Berechnen Sie $ \ beta_k = \ frac {g_ {k} ^ {T} g_k} {d_ {k} ^ {T} Qd_k} $

Berechnen Sie $ x_ {k + 1} = x_k + \ alpha_kd_k $

Setze $ g_ {k + 1} = x_k + \ alpha_kQd_k $

Berechnen Sie $ \ beta_k = \ frac {g_ {k + 1} ^ {T} g_ {k + 1}} {g_ {k} ^ {T} gk} $

Setze $ d_ {k + 1} = - g_ {k + 1} + \ beta_kd_k $.