Kosmologie - Kurzanleitung

Cosmologyist das Studium des Universums. In der Zeit zurück gab es mehrere Denkschulen bezüglich des Ursprungs des Universums. Viele Gelehrte glaubten an dieSteady State Theory. Nach dieser Theorie war das Universum immer das gleiche, es hatte keinen Anfang.

Während es eine Gruppe von Menschen gab, die Vertrauen in die hatten Big Bang Theory. Diese Theorie sagt den Beginn des Universums voraus. Es gab Hinweise auf heiße, ausgelassene Strahlung vom Urknall, was das Modell erneut unterstützt. Die Urknalltheorie sagt die Fülle der Lichtelemente im Universum voraus. Nach dem berühmten Modell des Urknalls können wir also feststellen, dass das Universum einen Anfang hatte. Wir leben in einem expandierenden Universum.

Die Hubble-Rotverschiebung

In den frühen 1900er Jahren wurde das hochmoderne Teleskop, Mt Wilson, ein 100-Zoll-Teleskop, war damals das größte Teleskop. Hubble war einer der prominenten Wissenschaftler, die mit diesem Teleskop arbeiteten. Er entdeckte, dass es außerhalb der Milchstraße Galaxien gab.Extragalactic Astronomyist nur 100 Jahre alt. Mt. Wilson war das größte Teleskop, bis das Palmer Observatory mit einem 200-Zoll-Teleskop gebaut wurde.

HubbleHumason war nicht die einzige Person, die Galaxien außerhalb der Milchstraße beobachtete. Er half ihm. Sie machten sich daran, die Spektren nahegelegener Galaxien zu messen. Sie beobachteten dann, dass ein galaktisches Spektrum im sichtbaren Wellenlängenbereich mit kontinuierlicher Emission lag. Auf dem Kontinuum befanden sich Emissions- und Absorptionslinien. Aus diesen Linien können wir abschätzen, ob sich die Galaxie von uns weg oder auf uns zubewegt.

Wenn wir ein Spektrum erhalten, nehmen wir an, dass die stärkste Linie von kommt H-α. Aus der Literatur sollte die stärkste Linie bei auftreten6563 Å, aber wenn die Linie irgendwo in der Nähe auftritt 7000Åkönnen wir leicht sagen, dass es rotverschoben ist.

Von dem Special Theory of Relativity,

$$ 1 + z = \ sqrt {\ frac {1+ \ frac {v} {c}} {1- \ frac {v} {c}}} $$

Dabei ist Z die Rotverschiebung, eine dimensionslose Zahl und v die Rezessionsgeschwindigkeit.

$$ \ frac {\ lambda_ {obs}} {\ lambda_ {rest}} = 1 + z $$

Hubble und Humason sind unten aufgeführt 22 Galaxiesin ihrer Zeitung. Fast alle diese Galaxien zeigten eine Rotverschiebung. Sie zeichneten die Geschwindigkeit (km / s) gegen die Entfernung (Mpc) auf. Sie beobachteten einen linearen Trend und Hubble stellte sein berühmtes Gesetz wie folgt vor.

$$ v_r = H_o d $$

Dies ist das Hubble Redshift Distance Relationship. Der Indexrzeigt an, dass die Ausdehnung in radialer Richtung erfolgt. Während $ v_r $ die zurückgehende Geschwindigkeit ist, ist $ H_o $ der Hubble-Parameter.dist die Entfernung der Galaxie von uns. Sie kamen zu dem Schluss, dass weit entfernte Galaxien schneller von uns zurücktreten, wenn die Expansionsrate für das Universum einheitlich ist.

Die Erweiterung

Alles bewegt sich von uns weg. Die Galaxien sind nicht stationär, es gibt immer eine gewisse harmonische Ausdehnung. Die Einheiten des Hubble-Parameters sind km sec ⁻¹ Mpc ⁻¹ . Wenn man eine Entfernung von - 1 Mpc verlässt, bewegen sich Galaxien mit einer Geschwindigkeit von 200 km / s. Der Hubble-Parameter gibt die Expansionsrate an. Gemäß Hubble und Humason beträgt der Wert von $ H_o $ 200 km / s / Mpc.

Die Daten zeigten, dass sich alle Galaxien von uns entfernen. Somit ist es offensichtlich, dass wir uns im Zentrum des Universums befinden. Aber Hubble hat diesen Fehler nicht gemacht, wie auch immer, in jeder Galaxie, in der wir leben, würden wir alle anderen Galaxien finden, die sich von uns entfernen. Die Schlussfolgerung ist also, dass sich der Raum zwischen den Galaxien ausdehnt und es kein Zentrum des Universums gibt.

Die Erweiterung findet überall statt. Es gibt jedoch einige Kräfte, die sich der Expansion widersetzen. Chemische Bindungen, Gravitationskraft und andere Anziehungskräfte halten Objekte zusammen. Früher waren alle Objekte nahe beieinander. Betrachtet man den Urknall als eine impulsive Kraft, so bewegen sich diese Objekte voneinander weg.

Zeitstrahl

Auf lokaler Ebene wird die Kinematik von der Schwerkraft bestimmt. Im ursprünglichen Hubble-Gesetz gab es einige Galaxien, die eine Blauverschiebung zeigten. Dies ist auf das kombinierte Gravitationspotential der Galaxien zurückzuführen. Die Schwerkraft hat die Dinge vom Hubble-Gesetz entkoppelt. Die Andromeda-Galaxie kommt auf uns zu. Die Schwerkraft versucht, die Dinge zu verlangsamen. Anfangs verlangsamte sich die Expansion, jetzt beschleunigt sie sich.

Da war ein Cosmic Jerkdeswegen. Für den Hubble-Parameter wurden mehrere Schätzungen vorgenommen. Es hat sich in den 90 Jahren von 500 km / s / Mpc auf 69 km / s / Mpc entwickelt. Die Ungleichheit im Wert war auf die Unterschätzung der Entfernung zurückzuführen. DasCepheid Stars wurden als Distanzkalibratoren verwendet, es gibt jedoch verschiedene Arten von Cepheid-Sternen, und diese Tatsache wurde bei der Schätzung des Hubble-Parameters nicht berücksichtigt.

Hubble-Zeit

Die Hubble-Konstante gibt uns eine realistische Schätzung des Alters des Universums. Das $ H_o $ würde das Alter des Universums angeben, vorausgesetzt, die Galaxien haben sich mit der gleichen Geschwindigkeit bewegt. Die Umkehrung von $ H_o $ gibt uns Hubble-Zeit.

$$ t_H = \ frac {1} {H_o} $$

Ersetzt man den Barwert von $ H_o, t_H $ = 14Milliarden Jahre. Die Expansionsrate war zu Beginn des Universums konstant. Auch wenn dies nicht der Fall ist, gibt $ H_o $ eine nützliche Grenze für das Alter des Universums. Unter der Annahme einer konstanten Expansionsrate ist die Steigung des Graphen durch die Geschwindigkeit gegeben, wenn wir einen Graphen zwischen Entfernung und Zeit zeichnen.

In diesem Fall entspricht die Hubble-Zeit der tatsächlichen Zeit. Wenn sich das Universum in der Vergangenheit schneller und in der Gegenwart langsamer ausgedehnt hätte, gibt die Hubble-Zeit eine Altersobergrenze des Universums an. Wenn sich das Universum zuvor langsam ausdehnte und jetzt schneller wurde, gibt die Hubble-Zeit eine Untergrenze für das Alter des Universums.

• $ t_H = t_ {age} $ - wenn die Expansionsrate konstant ist.

• $ t_H> t_ {age} $ - wenn sich das Universum in der Vergangenheit schneller und in der Gegenwart langsamer ausgedehnt hat.

• $ t_H <t_ {age} $ - wenn sich das Universum in der Vergangenheit langsamer und in der Gegenwart schneller ausgedehnt hat.

Stellen Sie sich eine Gruppe von 10 Galaxien vor, die 200 Mpc von einer anderen Gruppe von Galaxien entfernt sind. Die Galaxien innerhalb eines Clusters schließen niemals, dass sich das Universum ausdehnt, da die Kinematik innerhalb einer lokalen Gruppe von der Gravitation bestimmt wird.

Punkte, die man sich merken sollte

• Kosmologie ist das Studium der Vergangenheit, Gegenwart und Zukunft unseres Universums.

• Unser Universum ist 14 Milliarden Jahre alt.

• Das Universum wächst kontinuierlich.

• Der Hubble-Parameter ist ein Maß für das Alter des Universums.

• Aktueller Wert von H_o beträgt 69 km / s / mpc.

Lange Zeit betrachtete niemand Galaxien als außerhalb unserer Milchstraße präsent. Im Jahr 1924 entdeckte Edwin HubbleCepheid’sim Andromeda-Nebel und schätzte ihre Entfernung. Er kam zu dem Schluss, dass diese "Spiralnebel" tatsächlich andere Galaxien waren und nicht Teil unserer Milchstraße. Daher stellte er fest, dass M31 (Andromeda Galaxy) ein Inseluniversum ist. Dies war die Geburt vonExtragalactic Astronomy.

Cepheids Show a periodic dip in their brightness. Beobachtungen zeigen, dass die Periode zwischen aufeinanderfolgenden Einbrüchen, die als Pulsationsperiode bezeichnet wird, mit der Leuchtkraft zusammenhängt. Sie können also als Entfernungsindikatoren verwendet werden. Die Hauptreihensterne wie die Sonne befinden sich im hydrostatischen Gleichgewicht und verbrennen Wasserstoff in ihrem Kern. Nachdem Wasserstoff vollständig verbrannt ist, bewegen sich die Sterne in Richtung der Phase des Roten Riesen und versuchen, ihr Gleichgewicht wieder herzustellen.

Cepheid-Sterne sind Post-Main-Sequence-Sterne, die von den Main-Sequence-Sternen zu den Red Giants wechseln.

Klassifikation der Cepheiden

Es gibt 3 breite Klassen dieser pulsierenden variablen Sterne -

• Type-I Cepheids (oder klassische Cepheiden) - Zeitraum von 30-100 Tagen.

• Type-II Cepheids (oder W Virginis Stars) - Zeitraum von 1-50 Tagen.

• RR Lyrae Stars - Zeitraum von 0,1-1 Tag.

Zu diesem Zeitpunkt war Hubble diese Klassifizierung variabler Sterne nicht bekannt. Deshalb gab es eine Überschätzung der Hubble-Konstante, weshalb er ein niedrigeres Alter unseres Universums schätzte. Daher wurde auch die Rezessionsgeschwindigkeit überschätzt. Bei Cepheiden breiten sich die Störungen vom Zentrum des Sterns radial nach außen aus, bis das neue Gleichgewicht erreicht ist.

Beziehung zwischen Helligkeit und Pulsationsperiode

Versuchen wir nun, die physikalische Grundlage der Tatsache zu verstehen, dass eine höhere Pulsationsperiode mehr Helligkeit impliziert. Betrachten Sie einen Stern der Leuchtkraft L und der Masse M.

Wir wissen das -

$$ L \ propto M ^ \ alpha $$

wobei α = 3 bis 4 für Sterne mit geringer Masse ist.

Von dem Stefan Boltzmann Law, wir wissen das -

$$ L \ propto R ^ 2 T ^ 4 $$

Wenn R ist der Radius und $ c_s $ ist die Schallgeschwindigkeit, dann die Pulsationsperiode P kann geschrieben werden als -

$$ P = R / c_s $$

Die Schallgeschwindigkeit durch jedes Medium kann jedoch als Temperatur ausgedrückt werden als -

$$ c_s = \ sqrt {\ frac {\ gamma P} {\ rho}} $$

Hier, γ ist 1 für isotherme Fälle.

Für ein ideales Gas ist P = nkT, wobei k das ist Boltzmann Constant. Also können wir schreiben -

$$ P = \ frac {\ rho kT} {m} $$

wobei $ \ rho $ die Dichte ist und m ist die Masse eines Protons.

Daher ist der Zeitraum gegeben durch -

$$ P \ cong \ frac {Rm ^ {\ frac {1} {2}}} {(kT) ^ {{\ frac {1} {2}}} $$

Virial Theorem gibt an, dass für eine stabile, selbstgravitierende, sphärische Verteilung von Objekten gleicher Masse (wie Sterne, Galaxien) die gesamte kinetische Energie gilt k des Objekts entspricht minus der Hälfte der gesamten potentiellen Energie der Gravitation udh

$$ u = -2k $$

Nehmen wir an, dass der Virialsatz für diese variablen Sterne gilt. Wenn wir ein Proton direkt auf der Oberfläche des Sterns betrachten, können wir aus dem Virialsatz sagen:

$$ \ frac {GMm} {R} = mv ^ 2 $$

Aus der Maxwell-Distribution,

$$ v = \ sqrt {\ frac {3kT} {2}} $$

Daher Zeitraum -

$$ P \ sim \ frac {RR ^ {\ frac {1} {2}}} {(GM) ^ {\ frac {1} {2}}} $$

was impliziert

$$ P \ propto \ frac {R ^ {\ frac {3} {2}}} {M ^ {\ frac {1} {2}}} $$

Wir wissen, dass - $ M \ propto L ^ {1 / \ alpha} $

Auch $ R \ propto L ^ {1/2} $

So für β > 0, wir bekommen endlich - $ P \ propto L ^ \ beta $

Punkte, die man sich merken sollte

• Cepheid-Sterne sind Post-Main-Sequence-Sterne, die von den Main-Sequence-Sternen zu Red Giants wechseln.

• Es gibt drei Arten von Cepheiden: Typ I, Typ II, RR-Lyrae in absteigender Reihenfolge der Pulsationsperiode.

• Die Pulsationsperiode von Cepheid ist direkt proportional zu seiner Helligkeit (Leuchtkraft).

Hubbles Beobachtungen nutzten die Tatsache, dass die Radialgeschwindigkeit mit der Verschiebung der Spectral Lines. Hier werden wir vier Fälle beobachten und eine Beziehung zwischen der Rezessionsgeschwindigkeit ($ v_r $) und der Rotverschiebung (z) finden.

Fall 1: Nicht-relativistischer Fall der Quellenbewegung

In diesem Fall ist v viel kleiner als c. Die Quelle sendet ein Signal (Ton, Licht usw.) aus, das sich als ausbreitetWavefronts. Das Zeitintervall zwischen dem Senden von zwei aufeinanderfolgenden Signalen im Quellrahmen beträgtΔts. Das Zeitintervall zwischen dem Empfang von zwei aufeinanderfolgenden Signalen im Beobachterrahmen beträgtΔto.

Wenn sowohl der Beobachter als auch die Quelle stationär sind, ist Δts = Δto, aber dies ist hier nicht der Fall. Stattdessen ist die Beziehung wie folgt.

$$ \ Delta t_o = \ Delta t_s + \ frac {\ Delta l} {c} $$

Nun ist $ \ Delta l = v \ Delta t_s $

Da (Wellengeschwindigkeit x Zeit) = Wellenlänge, erhalten wir auch

$$ \ frac {\ Delta t_o} {\ Delta t_s} = \ frac {\ lambda_o} {\ lambda_s} $$

Aus den obigen Gleichungen erhalten wir die folgende Beziehung:

$$ \ frac {\ lambda_o} {\ lambda_s} = 1 + \ frac {v} {c} $$

Dabei ist $ \ lambda _s $ die Wellenlänge des Signals an der Quelle und $ \ lambda _o $ die Wellenlänge des Signals, wie sie vom Beobachter interpretiert wird.

Hier, da sich die Quelle vom Beobachter entfernt, v ist positiv.

Rotverschiebung -

$$ z = \ frac {\ lambda_o - \ lambda_s} {\ lambda_s} = \ frac {\ lambda_o} {\ lambda_s} - 1 $$

Aus den obigen Gleichungen erhalten wir die Rotverschiebung wie folgt.

$$ z = \ frac {v} {c} $$

Fall 2: Nicht-relativistischer Fall einer Beobachterbewegung

In diesem Fall ist v viel kleiner als c. Hier ist $ \ Delta l $ anders.

$$ \ Delta l = v \ Delta t_o $$

Bei Vereinfachung erhalten wir -

$$ \ frac {\ Delta t_o} {\ Delta t_s} = \ left (1 - \ frac {v} {c} \ right) ^ {- 1} $$

Wir bekommen Rotverschiebung wie folgt -

$$ z = \ frac {v / c} {1-v / c} $$

Schon seit v << cist der Rotverschiebungsausdruck für Fall I und Fall II ungefähr gleich.

Lassen Sie uns sehen, wie sich die Rotverschiebungen in den beiden oben genannten Fällen unterscheiden.

$$ z_ {II} - z_I = \ frac {v} {c} \ left [\ frac {1} {1 - v / c} -1 \ right] $$

Daher ist $ z_ {II} - z_ {I} $ aufgrund des Faktors $ (v / c) ^ 2 $ eine sehr kleine Zahl.

Dies impliziert, dass wir bei v << c nicht sagen können, ob sich die Quelle oder der Beobachter bewegt.

Lassen Sie uns jetzt das verstehen Basics of STR (Spezielle Relativitätstheorie) -

• Lichtgeschwindigkeit ist eine Konstante.

• Wenn sich die Quelle (oder der Beobachter) mit einer Geschwindigkeit bewegt, die mit der Lichtgeschwindigkeit vergleichbar ist, werden relativistische Effekte beobachtet.

• Zeitdilatation: $ \ Delta t_o = \ gamma \ Delta t_s $

• Längenkontraktion: $ \ Delta l_o = \ Delta t_s / \ gamma $

• Hier ist $ \ gamma $ das Lorrentz factorgrößer als 1.

$$ \ gamma = \ frac {1} {\ sqrt {1- (v ^ 2 / c ^ 2)}} $$

Fall 3: Relativistischer Fall der Quellenverschiebung

In diesem Fall ist v vergleichbar mit c. Beziehen Sie sich auf dieselbe Figur wie in Fall I. Aufgrund des relativistischen Effekts wird eine Zeitdilatation beobachtet und daher wird die folgende Beziehung erhalten. (Quelle bewegt sich mit relativistischer Geschwindigkeit)

$$ \ Delta t_o = \ gamma \ Delta t_s + \ frac {\ Delta l} {c} $$

$$ \ Delta l = \ frac {v \ gamma \ Delta t_s} {c} $$

$$ \ frac {\ Delta t_o} {\ Delta t_s} = \ frac {1 + v / c} {\ sqrt {1- (v ^ 2 / c ^ 2)}} $$

Bei weiterer Vereinfachung erhalten wir:

$$ 1 + z = \ sqrt {\ frac {1 + v / c} {1-v / c}} $$

Der obige Ausdruck ist bekannt als Kinematic Doppler Shift Expression.

Fall 4: Relativistischer Fall der Beobachterbewegung

Beziehen Sie sich auf die gleiche Abbildung wie in Fall II. Aufgrund des relativistischen Effekts wird eine Zeitverkürzung beobachtet und daher wird die folgende Beziehung erhalten. (Beobachter bewegt sich mit relativistischer Geschwindigkeit)

$$ \ Delta t_o = \ frac {\ Delta t_s} {\ gamma} + \ frac {\ Delta l} {c} $$

$$ \ Delta l = \ frac {v \ Delta t_o} {c} $$

$$ \ frac {\ Delta t_o} {\ Delta t_s} = \ frac {\ sqrt {1- (v ^ 2 / c ^ 2)}} {1-v / c} $$

Bei weiterer Vereinfachung erhalten wir -

$$ 1 + z = \ sqrt {\ frac {1+ v / c} {1- v / c}} $$

Der obige Ausdruck ist der gleiche wie der, den wir für Fall III erhalten haben.

Punkte, die man sich merken sollte

• Rezessionsgeschwindigkeit und Rotverschiebung eines Sterns sind verwandte Größen.

• In einem nicht relativistischen Fall können wir nicht feststellen, ob sich die Quelle bewegt oder stationär ist.

• In einem relativistischen Fall gibt es keinen Unterschied in der Rotverschiebungs-Rezessions-Geschwindigkeitsbeziehung für die Bewegung der Quelle oder des Beobachters.

• Bewegliche Uhren bewegen sich langsamer, ist ein direktes Ergebnis der Relativitätstheorie.

Eine Galaxie, die sich in Rotverschiebung befindet z = 10, entspricht v≈80% von c. Die Masse der Milchstraße ist da1011M⊙Wenn wir die dunkle Materie betrachten, ist es das 1012M⊙. Unsere Milchstraße ist also massiv. Wenn es sich bei 80% bewegtcEs passt nicht in das allgemeine Konzept, wie sich Objekte bewegen.

Wir wissen,

$$ \ frac {v_r} {c} = \ frac {\ lambda_ {obs} - \ lambda {rest}} {\ lambda_ {rest}} $$

Für kleine Werte von z,

$$ z = \ frac {v_r} {c} = \ frac {\ lambda_ {obs} - \ lambda_ {rest}} {\ lambda_ {rest}} $$

In der folgenden Grafik, der Klasse zwischen Fluss und Wellenlänge, befinden sich Emissionslinien über dem Kontinuum. Von demH-α Linieninformationen können wir daraus grob schließen z = 7. Dies impliziert, dass sich die Galaxie zu 70% bewegtc. Wir beobachten eine Verschiebung und interpretieren sie als Geschwindigkeit. Wir sollten diesen Gedanken loswerden und uns das ansehenzauf andere Weise. Stellen Sie sich den Raum als 2D-Gitter vor, das das Universum wie unten gezeigt darstellt.

Betrachten Sie den schwarzen Stern als unsere eigene Milchstraße und den blauen Stern als eine andere Galaxie. Wenn wir Licht von dieser Galaxie aufnehmen, sehen wir das Spektrum und finden seine Rotverschiebung heraus, dh die Galaxie bewegt sich weg. Wenn das Photon emittiert wurde, hatte es eine relative Geschwindigkeit.

• Was wäre, wenn sich der Raum erweitern würde?

• Es ist eine sofortige Rotverschiebung des Photons. Kumulative Rotverschiebungen entlang des Raums zwischen zwei Galaxien führen zu einer großen Rotverschiebung. Die Wellenlänge wird sich schließlich ändern. Es ist eher die Erweiterung des Raumes als die kinematische Bewegung der Galaxien.

Das folgende Bild zeigt, wenn die gegenseitige Schwerkraft die Expansion überläuft, ist dies nicht Teil des Hubble-Gesetzes.

Bei der kinematischen Doppler-Verschiebung wird die Rotverschiebung zum Zeitpunkt der Emission in einem Photon induziert. Bei einer kosmologischen Rotverschiebung wird sie in jedem Schritt kumulativ rot verschoben. In einem Gravitationspotential wird ein Photon blau verschoben. Wenn es aus dem Gravitationspotential herauskriecht, verschiebt es sich rot.

Gemäß einer speziellen Relativitätstheorie können zwei Objekte, die aneinander vorbeigehen, keine Relativgeschwindigkeit haben, die größer als die Lichtgeschwindigkeit ist. Die Geschwindigkeit, über die wir sprechen, ist von der Expansion des Universums. Für große Werte von z ist die Rotverschiebung kosmologisch und kein gültiges Maß für die tatsächliche Rezessionsgeschwindigkeit des Objekts in Bezug auf uns.

Das kosmologische Prinzip

Es stammt aus dem Copernicus Notiondes Universums. Nach dieser Vorstellung ist das Universum homogen und isotrop. Es gibt keine bevorzugte Richtung und Position im Universum.

• Homogenität bedeutet, egal in welchem ​​Teil des Universums Sie sich befinden, Sie werden sehen, dass das Universum in allen Teilen gleich ist. Isotrope Natur bedeutet, dass Sie unabhängig von der Blickrichtung dieselbe Struktur sehen werden.

• Ein passendes Beispiel für Homogenität ist ein Reisfeld. Es sieht von allen Seiten homogen aus, aber wenn Wind fließt, gibt es Abweichungen in seiner Ausrichtung, so dass es nicht isotrop ist. Stellen Sie sich einen Berg auf einem flachen Land vor und ein Beobachter steht auf dem Berggipfel. Er wird die isotrope Natur des flachen Landes sehen, aber es ist nicht homogen. Wenn es in einem homogenen Universum an einem Punkt isotrop ist, ist es überall isotrop.

• Es wurden groß angelegte Umfragen durchgeführt, um das Universum abzubilden. Sloan Digital Sky Surveyist eine solche Umfrage, die sich nicht viel auf die Deklination konzentrierte, sondern auf den richtigen Aufstieg. Die Lookback-Zeit beträgt rund 2 Milliarden Jahre. Jedes Pixel entspricht dem Ort einer Galaxie und die Farbe entspricht der morphologischen Struktur. Die grüne Farbe stellte die blaue Spiralgalaxie dar, während die rote falsche Farbe massive Galaxien anzeigte.

• Galaxien befinden sich in einer Filamentstruktur in einem kosmologischen Netz und es gibt Hohlräume zwischen den Galaxien.

• $ \ delta M / M \ cong 1 $ dh die Schwankung der Massenverteilung beträgt 1 M ist die Masse der Materie, die in einem gegebenen Würfel vorhanden ist. Nehmen Sie in diesem Fall den Volume 50 Mpc-Würfel.

• Für eine Würfelseite von 1000 Mpc ist $ \ delta M / M \ cong 10 ^ {- 4} $.

• Eine Möglichkeit zur Quantifizierung der Homogenität besteht darin, Massenschwankungen zu erfassen. Massenschwankungen sind bei niedrigeren Maßstäben höher.

• Berücksichtigen Sie zur Quantifizierung der isotropen Natur die kosmische Mikrowellen-Hintergrundstrahlung. Das Universum ist bei großen Winkelskalen nahezu isotrop.

Punkte, die man sich merken sollte

• Zwei Objekte, die aneinander vorbeigehen, können keine Relativgeschwindigkeit haben, die größer als die Lichtgeschwindigkeit ist.

• Das kosmologische Prinzip besagt, dass das Universum homogen und isotrop ist.

• Diese Homogenität besteht in einem sehr großen Winkelmaßstab und nicht in kleineren Maßstäben.

• SDSS (Sloan Digital Sky Survey) ist ein Versuch, den Nachthimmel abzubilden und das kosmologische Prinzip zu verifizieren.

Gemäß dem Gesetz der Energieerhaltung und dem Gesetz der Massenerhaltung bleibt die Gesamtenergiemenge einschließlich der Masse (E = mc ² ) während jedes Schritts in einem Prozess im Universum unverändert. Die Expansion des Universums selbst verbraucht Energie, die möglicherweise aus der Dehnung der Wellenlänge von Photonen (kosmologische Rotverschiebung), Wechselwirkungen mit dunkler Energie usw. resultiert.

Um die Vermessung von mehr als 26.000 Galaxien zu beschleunigen, Stephen A. Shectmanentwarf ein Instrument, mit dem 112 Galaxien gleichzeitig gemessen werden können. In eine Metallplatte wurden Löcher gebohrt, die den Positionen der Galaxien am Himmel entsprachen. Glasfaserkabel führten das Licht von jeder Galaxie zu einem separaten Kanal auf einem Spektrographen am 2,5-Meter-Teleskop du Pont amCarnegie Observatories auf dem Cerro Las Campanas in Chile.

Für maximale Effizienz wird eine spezielle Technik verwendet, die als Drift-Scan Photometrywurde verwendet, bei dem das Teleskop auf den Beginn eines Vermessungsfeldes gerichtet und dann der automatische Antrieb ausgeschaltet wurde. Das Teleskop blieb stehen, als der Himmel vorbeizog. Computer lesen Informationen aus demCCD Detectormit der gleichen Geschwindigkeit wie die Erdrotation, wodurch ein langes, kontinuierliches Bild bei einem konstanten himmlischen Breitengrad erzeugt wird. Die Durchführung der Photometrie dauerte insgesamt 450 Stunden.

Es gibt verschiedene Arten von Rauschen, und ihre mathematische Modellierung hängt von ihren Eigenschaften ab. Verschiedene physikalische Prozesse entwickeln das Leistungsspektrum des Universums in großem Maßstab. Das anfängliche Leistungsspektrum, das aufgrund der Quantenschwankungen verliehen wird, folgt einer negativen dritten Potenz der Frequenz, die eine Form von istPink Noise Spectrum in drei Dimensionen.

Die Metrik

In der Kosmologie muss man zuerst eine Definition des Raumes haben. Eine Metrik ist ein mathematischer Ausdruck, der Punkte im Raum beschreibt. Die Beobachtung des Himmels erfolgt in einer sphärischen Geometrie; daher ist ein sphärisches Koordinatensystem zu verwenden. Der Abstand zwischen zwei eng beieinander liegenden Punkten ist gegeben durch -

$$ ds ^ 2 = dr ^ 2 + r ^ 2 \ theta ^ 2 + r ^ 2 sin ^ 2 \ theta d \ phi ^ 2 $$

Das folgende Bild zeigt die Geometrie im dreidimensionalen nicht expandierenden euklidischen Raum.

Diese Geometrie befindet sich immer noch im dreidimensionalen nicht expandierenden euklidischen Raum. Daher würde sich das Referenzraster, das den Rahmen selbst definiert, erweitern. Das folgende Bild zeigt die erhöhte Metrik.

In die Gleichung des nicht expandierenden Raums wird ein Skalierungsfaktor eingefügt, der als "Skalierungsfaktor" bezeichnet wird und die Ausdehnung des Universums in Bezug auf die Zeit beinhaltet.

$$ ds ^ 2 = a ^ 2 (t) \ left [dr ^ 2 + r ^ 2 \ theta ^ 2 + r ^ 2 sin ^ 2 \ theta d \ phi ^ 2 \ right] $$

wo a(t) ist der Skalierungsfaktor, manchmal geschrieben als R(t). Wohingegen,a(t) > 1 bedeutet Vergrößerung der Metrik, während a(t) < 1 bedeutet Schrumpfen der Metrik und a(t) = 1bedeutet konstante Metrik. Als Konvention,a(t₀) = 1.

Comoving Koordinatensystem

In einem Comoving Coordinate System, Die Messskala erweitert sich zusammen mit dem Rahmen (expandierendes Universum).

Hier ist der $ \ left [dr ^ 2 + r ^ 2 \ theta ^ 2 + r ^ 2 sin ^ 2 \ theta d \ phi ^ 2 \ right] $ der Comoving Distance und der $ ds ^ 2 $ der Richtiger Abstand.

Die richtige Entfernung entspricht der tatsächlichen Entfernung, die zum Zeitpunkt der Beobachtung von einer entfernten Galaxie von der Erde gemessen wurde, auch bekannt als augenblickliche Entfernung von Objekten.

Dies liegt daran, dass die Entfernung, die ein Photon zurücklegt, wenn es den Beobachter von einer entfernten Quelle erreicht, diejenige ist, die bei $ t = t_0 $ des Beobachters empfangen wird, was bedeuten würde, dass die augenblicklich beobachtete Entfernung die richtige Entfernung ist und man kann Vorhersage zukünftiger Entfernungen anhand des Ratenfaktors und der anfänglich gemessenen Länge als Referenz.

Das Konzept des Comoving und der richtigen Entfernung ist wichtig, um den tatsächlichen Wert der Zahlendichte von Galaxien in dem gegebenen Volumen des beobachteten Raums zu messen. Man muss den Comoving-Abstand verwenden, um die Dichte zum Zeitpunkt ihrer Bildung zu berechnen, als das beobachtete Photon emittiert wurde. Dies kann erreicht werden, sobald die Expansionsrate des Universums geschätzt werden kann.

Um die Expansionsrate abzuschätzen, kann man die Änderung der Entfernung einer beobachteten entfernten Galaxie über einen langen Zeitraum beobachten.

Punkte, die man sich merken sollte

• Eine Metrik ist ein mathematischer Ausdruck, der die Punkte im Raum beschreibt.

• Der Skalierungsfaktor bestimmt, ob sich das Universum zusammenzieht oder ausdehnt.

• In einem kommenden Koordinatensystem dehnt sich die Messskala zusammen mit dem Rahmen aus (expandierendes Universum).

• Die richtige Entfernung ist die momentane Entfernung von Objekten.

• Die Entfernung ist die tatsächliche Entfernung von Objekten.

In diesem Kapitel werden wir die Robertson-Walker-Metrik im Detail verstehen.

Modell für den Skalierungsfaktor, der sich mit der Zeit ändert

Angenommen, ein Photon wird von einer entfernten Galaxie emittiert. Der Raum ist für Photonen in alle Richtungen vorwärts. Die Expansion des Universums erfolgt in alle Richtungen. Lassen Sie uns in den folgenden Schritten sehen, wie sich der Skalierungsfaktor mit der Zeit ändert.

Step 1 - Für ein statisches Universum beträgt der Skalierungsfaktor 1, dh der Wert der mitkommenden Entfernung ist die Entfernung zwischen den Objekten.

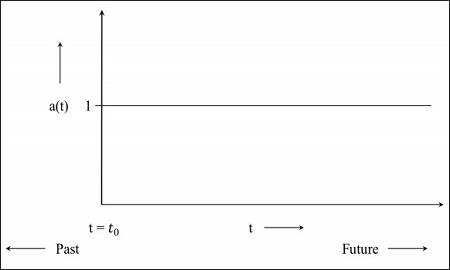
Step 2- Das folgende Bild ist das Diagramm des Universums, das sich immer noch ausdehnt, jedoch mit abnehmender Geschwindigkeit, was bedeutet, dass das Diagramm in der Vergangenheit beginnt. Dast = 0 zeigt an, dass das Universum von diesem Punkt aus gestartet ist.

Step 3 - Das folgende Bild ist die Grafik für das Universum, das sich schneller ausdehnt.

Step 4 - Das folgende Bild ist die Grafik für das Universum, das sich ab sofort zusammenzieht.

Wenn der Wert des Skalierungsfaktors wird 0 Während der Kontraktion des Universums impliziert dies, dass der Abstand zwischen den Objekten wird 0dh der richtige Abstand wird 0. Die kommende Entfernung, die die Entfernung zwischen den Objekten in einem gegenwärtigen Universum ist, ist eine konstante Größe. In der Zukunft, wenn der Skalierungsfaktor wird0wird alles näher kommen. Das Modell hängt von der Komponente des Universums ab.

Die Metrik für das flache (euklidische: es gibt keinen Parameter für die Krümmung) expandierende Universum ist gegeben als -

$$ ds ^ 2 = a ^ 2 (t) \ left (dr ^ 2 + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2 \ right) $$

Für Raum-Zeit wird das Linienelement, das wir in der obigen Gleichung erhalten haben, modifiziert als -

$$ ds ^ 2 = c ^ 2dt ^ 2 - \ left \ {a ^ 2 (t) \ left (dr ^ 2 + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2 \ rechts) \ rechts \} $$

Für die Raumzeit ist die Zeit, zu der das Photon emittiert wird und wann es detektiert wird, unterschiedlich. Die richtige Entfernung ist die momentane Entfernung zu Objekten, die sich im Laufe der Zeit aufgrund der Expansion des Universums ändern kann. Es ist die Entfernung, die das Photon von verschiedenen Objekten zurückgelegt hat, um zu uns zu gelangen. Es bezieht sich auf die kommende Entfernung als -

$$ d_p = a (t) \ times d_c $$

Dabei ist $ d_p $ der richtige Abstand und $ d_c $ der festgelegte Abstand, der fest ist.

Die gemessene Entfernung zu den Objekten im gegenwärtigen Universum wird als kommende Entfernung genommen, was bedeutet, dass die kommende Entfernung fest ist und durch die Expansion unverändert bleibt. In der Vergangenheit war der Skalierungsfaktor kleiner als 1, was darauf hinweist, dass der richtige Abstand kleiner war.

Wir können die Rotverschiebung zu einer Galaxie messen. Daher entspricht der richtige Abstand $ d_p $ $ c \ mal t (z) $, wobei $ t (z) $ die Rückblickzeit auf eine Rotverschiebung und c die Lichtgeschwindigkeit im Vakuum ist. Die Lookback-Zeit ist eine Funktion der Rotverschiebung(z).

Lassen Sie uns anhand des obigen Begriffs analysieren, wie die kosmologische Rotverschiebung in diesem Szenario von $ d_p = a (t) \ times d_c $ interpretiert wird.

Angenommen, ein Photon (das erdgebunden ist) wird von der Galaxie G emittiert. Das $ t_ {em} $ entspricht der Zeit, zu der das Photon emittiert wurde; $ a (t_ {em}) $ war der Skalierungsfaktor zu dem Zeitpunkt, als das Photon emittiert wurde. Zum Zeitpunkt der Detektion des Photons hatte sich das gesamte Universum ausgedehnt, dh das Photon ist zum Zeitpunkt der Detektion rotverschoben. Das $ t_ {obs} $ entspricht der Zeit, zu der das Photon detektiert wird und der entsprechende Skalierungsfaktor ist $ a (t_ {obs}) $.

Der Faktor, um den das Universum gewachsen ist, ist gegeben durch -

$$ \ frac {a (t_ {obs})} {a (t_ {em})} $$

Der Faktor, um den sich die Wellenlänge erweitert hat, ist -

$$ \ frac {\ lambda_ {obs}} {\ lambda_ {em}} $$

Das ist gleich dem Faktor, um den das Universum gewachsen ist. Die Symbole haben ihre übliche Bedeutung. Deshalb,

$$ \ frac {a (t_ {obs})} {a (t_ {em})} = \ frac {\ lambda_ {obs}} {\ lambda_ {em}} $$

Wir kennen diese Rotverschiebung (z) ist -

$$ z = \ frac {\ lambda_ {obs} - \ lambda_ {em}} {\ lambda_ {em}} = \ frac {\ lambda_ {obs}} {\ lambda_ {em}} - 1 $$

$$ 1 + z = \ frac {a (t_ {obs})} {a (t_ {em})} $$

Der gegenwärtige Wert des Skalierungsfaktors ist 1, daher ist $ a (t_ {obs}) = 1 $ und bezeichnet den Skalierungsfaktor, als in der Vergangenheit Photonen emittiert wurden, mit $ a (t) $.

Deshalb,

$$ 1 + z = \ frac {1} {a (t)} $$

Interpretation der Rotverschiebung in der Kosmologie

Um dies zu verstehen, nehmen wir das folgende Beispiel: Wenn $ z = 2 $, dann ist $ a (t) = 1/3 $.

Dies impliziert, dass sich das Universum um den Faktor drei erweitert hat, seit das Licht dieses Objekt verlassen hat. Die Wellenlänge der empfangenen Strahlung hat sich um den Faktor drei vergrößert, da sich der Raum während seines Transits vom emittierenden Objekt um den gleichen Faktor vergrößert hat. Es ist zu beachten, dass bei so großen Werten vonzDie Rotverschiebung ist hauptsächlich die kosmologische Rotverschiebung und kein gültiges Maß für die tatsächliche Rezessionsgeschwindigkeit des Objekts in Bezug auf uns.

Für kosmischen Mikrowellenhintergrund (CMB), z = 1089, was bedeutet, dass sich das gegenwärtige Universum um einen Faktor von erweitert hat ∼1090. Die Metrik für das flache, euklidische, expandierende Universum lautet:

$$ ds ^ 2 = a ^ 2 (t) (dr ^ 2 + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2) $$

Wir möchten die Metrik in jeder Krümmung schreiben.

Robertson and Walker Für jedes Krümmungsuniversum (das homogen und isotrop ist) ist die Metrik gegeben als -

$$ ds ^ 2 = a ^ 2 (t) \ left [\ frac {dr ^ 2} {1-kr ^ 2} + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2 \ right] $$

Dies ist allgemein bekannt als die Robertson–Walker Metricund gilt für jede Topologie des Raumes. Bitte beachten Sie den zusätzlichen Faktor in $ dr ^ 2 $. Hier ist die Krümmungskonstante.

Geometrie des Universums

Die Geometrie des Universums wird mit Hilfe der folgenden Krümmungen erklärt, darunter:

• Positive Krümmung
• Negative Krümmung
• Null Krümmung

Lassen Sie uns jedes davon im Detail verstehen.

Positive Krümmung

Wenn sich eine Tangentialebene, die an einem beliebigen Punkt auf der Oberfläche der Krümmung gezeichnet ist, an keinem Punkt der Oberfläche schneidet, spricht man von einer Oberfläche mit einer positiven Krümmung, dh die Oberfläche bleibt an diesem Punkt auf einer Seite der Tangentialebene. Die Oberfläche der Kugel hat eine positive Krümmung.

Negative Krümmung

Wenn sich eine Tangentialebene, die an einem Punkt auf der Oberfläche der Krümmung gezeichnet ist, an einem beliebigen Punkt auf der Oberfläche schneidet, spricht man von einer Oberfläche mit negativer Krümmung, dh die Oberfläche krümmt sich von der Tangentialebene weg in zwei verschiedene Richtungen. Eine sattelförmige Oberfläche hat eine negative Krümmung.

Betrachten Sie nun die Oberfläche einer Kugel. Wenn ein Dreieck auf der Oberfläche der Kugel konstruiert wird, indem drei Punkte mit der Geodät (Bogen großer Kreise) verbunden werden, ist die Summe der Innenwinkel des sphärischen Dreiecks größer als 180 ^° , dh -

$$ \ alpha + \ beta + \ gamma> \ pi $$

Solche Räume werden positiv gekrümmte Räume genannt. Auch die Krümmung ist homogen und isotrop. Im Allgemeinen folgt der Winkel an den Eckpunkten des sphärischen Dreiecks der Beziehung -

$$ \ alpha + \ beta + \ gamma = \ pi + A / R ^ 2 $$

wo A ist die Fläche des Dreiecks und Rist der Radius der Kugel. Das folgende Bild zeigt einen positiv gekrümmten Raum.

Für eine positive Krümmung sollten sich die parallelen Linien treffen. Betrachten Sie die Erdoberfläche, die ein positiv gekrümmter Raum ist. Nehmen Sie zwei Startpunkte am Äquator. Die Linien, die den Äquator im rechten Winkel kreuzen, werden als Längengrade bezeichnet. Da diese Linien den Äquator rechtwinklig kreuzen, können sie als parallele Linien bezeichnet werden. Ausgehend vom Äquator kreuzen sie sich schließlich an den Polen. Diese Methode wurde von verwendetCarl Gauss und andere, um die Topologie der Erde zu verstehen.

Betrachten Sie einen negativ gekrümmten Raum (ein Sattel im folgenden Bild), die Summe der Innenwinkel des Dreiecks beträgt weniger als 180 ^° , dh -

$$ \ alpha + \ beta + \ gamma <\ pi $$

Der Winkel an den Eckpunkten folgt der Beziehung -

$$ \ alpha + \ beta + \ gamma = \ pi - A / R ^ 2 $$

Null Krümmung

Eine ebene Fläche hat keine Krümmung. Wenn für einen flachen Raum eine Ebene genommen und ein Dreieck konstruiert wird, indem drei Punkte mit geodätischen (geraden Linien) verbunden werden, beträgt die innere Winkelsumme -

$$ \ alpha + \ beta + \ gamma = \ pi $$

Das folgende Bild ist ein flacher zweidimensionaler Raum.

Wenn ein Raum homogen und isotrop sein soll, bleiben nur drei Möglichkeiten: Der Raum kann gleichmäßig flach sein oder eine gleichmäßige positive Krümmung oder eine gleichmäßige negative Krümmung aufweisen.

Die Krümmungskonstante kann einen der folgenden drei Werte annehmen.

$$ k = \ begin {Fälle} +1, & für \: a \: positiv \: gekrümmt \: Raum; \\\ Quad 0, & für \: a \: flach \: Raum; \\ - 1, & für \: a \: negativ \: gekrümmt \: Leerzeichen; \ end {Fälle} $$

Globale Topologie des Universums

Das Universum hat eine bestimmte Topologie, aber lokal kann es Falten haben. Abhängig davon, wie die Materie im Raum verteilt ist, gibt es kleinere Variationen in der Krümmung. Nehmen wir an, es gibt eine Klasse von Objekten, die unabhängig vom Ort im Universum dieselbe wahre Größe haben, was bedeutet, dass sie wie Standardkerzen sind. Sie haben nicht die gleiche Helligkeit, aber die gleiche Größe.

Befindet sich das Objekt in einem positiv gekrümmten Raum und kommen Photonen von Punkt A (ein Ende des Objekts) und B (anderes Ende des Objekts), breiten sich die Photonen im positiv gekrümmten Raum parallel über den geodätischen Pfad aus und treffen sich schließlich . Für einen Beobachter bei C scheint es, dass es von zwei verschiedenen Punkten in verschiedene Richtungen kam.

Wenn sich das Objekt im lokalen Universum befindet und wir die Winkelgröße messen, wird es nicht von der Krümmung beeinflusst. Wenn dieselbe Objektklasse bei einer größeren Rotverschiebung gesehen wird, korreliert die Winkelgröße nicht mit.

$$ \ theta = \ frac {d} {r} $$

Wo d ist die Größe des Objekts und rist der Abstand zum Objekt, dh wenn die Größe größer als die lokale Größe ist, bedeutet dies, dass die Krümmung positiv ist. Das folgende Bild ist eine Darstellung des in einem positiv gekrümmten Raum detektierten Photons.

Es ist anzumerken, dass es kein echtes astrophysikalisches Objekt gibt, das eine Standardgröße und -morphologie aufweist. Es wurde zwar angenommen, dass eine massive elliptische cD - Galaxie zu den Standardkerzen passt, aber es wurde auch festgestellt, dass sie sich mit der Zeit weiterentwickelt.

Entfernungen zu Galaxien finden

In diesem Abschnitt werden wir diskutieren, wie man die Entfernung zu einer Galaxie unter Berücksichtigung des folgenden Bildes ermittelt.

Betrachten Sie die Milchstraße bei (r, θ,) in einem kosmologischen Ruhezustand. Man kann = 0 nehmen; (0, θ, ϕ), dh das Zentrum des Universums unter Berufung auf die Annahme der Homogenität.

Betrachten Sie eine Galaxie 'G' bei (r1, θ,). Die Entfernung (richtig) ist die kürzeste radiale Entfernung, die ein Photon zurücklegt. Ausgehend von der Symmetrie von Raum und Zeit hat die Null-Geodät von r = 0 bis r = r1 eine konstante Richtung im Raum. In ihrer radialen Ausbreitung ändern sich die Winkelkoordinaten nicht. Wenn sich die Winkelkoordinaten ändern, ist dies nicht der kürzeste Weg. Dies ist der Grund, warum der Krümmungsterm in dr ^{2 vorhanden ist} .

Punkte, die man sich merken sollte

• Die Expansion des Universums erfolgt in alle Richtungen.

• Das Universum kann statisch sein, sich ausdehnen oder zusammenziehen, abhängig von der Entwicklung des Skalierungsfaktors.

• Die cD-Galaxien entwickeln sich mit der Zeit und können daher nicht als Standardkerzen verwendet werden.

• Das Universum hat eine bestimmte Topologie, aber lokal kann es Falten haben.

In diesem Kapitel werden wir sowohl den Hubble-Parameter als auch den Skalierungsfaktor diskutieren.

• Prerequisite - Kosmologische Rotverschiebung, kosmologische Prinzipien.

• Assumption - Das Universum ist homogen und isotrop.

Hubble-Konstante mit Bruchteil der Änderungsrate des Skalierungsfaktors

In diesem Abschnitt werden wir die Hubble-Konstante mit der gebrochenen Änderungsrate des Skalierungsfaktors in Beziehung setzen.

Wir können die Geschwindigkeit auf folgende Weise schreiben und vereinfachen.

$$ v = \ frac {\ mathrm {d} r_p} {\ mathrm {d} t} $$

$$ = \ frac {d [a (t) r_c} {dt} $$

$$ v = \ frac {\ mathrm {d} a} {\ mathrm {d} t} \ ast \ frac {1} {a} \ ast (ar_c) $$

$$ v = \ frac {\ mathrm {d} a} {\ mathrm {d} t} \ ast \ frac {1} {a} \ ast r_p $$

Hier, v ist die Rezessionsgeschwindigkeit, a ist der Skalierungsfaktor und r_p ist der richtige Abstand zwischen den Galaxien.

Hubble’s Empirical Formula war von der Natur -

$$ v = H \ ast r_p $$

Wenn wir also die beiden obigen Gleichungen vergleichen, erhalten wir -

Hubble’s Parameter = Fractional rate of change of the scale factor

$$ H = da / dt \ ast 1 / a $$

Note- Dies ist keine Konstante, da der Skalierungsfaktor eine Funktion der Zeit ist. Daher wird es als Hubble-Parameter und nicht als Hubble-Konstante bezeichnet.

Empirisch schreiben wir -

$$ H = V / D $$

Aus dieser Gleichung können wir also schließen, dass da D nimmt zu und V ist also eine Konstante H reduziert sich mit der Zeit und Expansion des Universums.

Friedmann-Gleichung in Verbindung mit dem Robertson-Walker-Modell

In diesem Abschnitt werden wir verstehen, wie die Friedmann-Gleichung in Verbindung mit dem Robertson-Walker-Modell verwendet wird. Um dies zu verstehen, nehmen wir das folgende Bild, das eine Testmasse in einiger Entfernung aufweistr_p vom Körper der Masse M als Beispiel.

Unter Berücksichtigung des obigen Bildes können wir Kraft ausdrücken als -

$$ F = G \ ast M \ ast \ frac {m} {r ^ 2_p} $$

Hier, G ist die universelle Gravitationskonstante und ρ ist die Materiedichte innerhalb des beobachtbaren Universums.

Unter der Annahme einer einheitlichen Massendichte innerhalb der Kugel können wir schreiben:

$$ M = \ frac {4} {3} \ ast \ pi \ ast r_p ^ 3 \ ast \ rho $$

Wenn wir diese in unserer Kraftgleichung verwenden, erhalten wir -

$$ F = \ frac {4} {3} \ ast \ pi \ ast G \ ast r_p \ ast \ rho \ ast m $$

Somit können wir die potentielle Energie und kinetische Energie der Masse schreiben m als -

$$ V = - \ frac {4} {3} \ ast \ pi \ ast G \ ast r ^ 2_p \ ast m \ ast \ rho $$

$$ KE = \ frac {1} {2} \ ast m \ ast \ frac {\ mathrm {d} r_p ^ 2} {\ mathrm {d} t} $$

Verwendung der Virial Theorem - -

$$ U = KE + V $$

$$ U = \ frac {1} {2} \ ast m \ ast \ left (\ frac {\ mathrm {d} r_p} {\ mathrm {d} t} \ right) ^ 2 - \ frac {4} { 3} \ ast \ pi \ ast G \ ast r_p ^ 2 \ ast m \ ast \ rho $$

Aber hier ist $ r_p = ar_c $. Also bekommen wir -

$$ U = \ frac {1} {2} \ ast m \ ast \ left (\ frac {\ mathrm {d} a} {\ mathrm {d} t} \ right) ^ 2 r_c ^ 2 - \ frac { 4} {3} \ ast \ pi \ ast G \ ast r_p ^ 2 \ ast m \ ast \ rho $$

Bei weiterer Vereinfachung erhalten wir die Friedmann-Gleichung,

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi} {3} \ ast G \ ast \ rho + \ frac {2U} {m} \ ast r_c ^ 2 \ ast a ^ 2 $$

Hier Uist eine Konstante. Wir stellen auch fest, dass das Universum, in dem wir gegenwärtig leben, von Materie dominiert wird, während die Strahlungsenergiedichte sehr niedrig ist.

Punkte, die man sich merken sollte

• Der Hubble-Parameter verringert sich mit der Zeit und der Erweiterung des Universums.

• Das Universum, in dem wir gegenwärtig leben, wird von Materie dominiert und die Strahlungsenergiedichte ist sehr gering.

In diesem Kapitel werden wir verstehen, was die Friedmann-Gleichung ist, und die Weltmodelle für verschiedene Krümmungskonstanten im Detail untersuchen.

Friedmann-Gleichung

Diese Gleichung sagt etwas über die Expansion des Raums in homogenen und isotropen Modellen des Universums aus.

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho + \ frac {2U} {mr_c ^ 2a ^ 2} $ $

Dies wurde im Zusammenhang mit geändert General Relativity (GR) und Robertson-Walker Metric wie folgt.

GR-Gleichungen verwenden -

$$ \ frac {2U} {mr_c ^ 2} = -kc ^ 2 $$

Wo kist die Krümmungskonstante. Deshalb,

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho - \ frac {kc ^ 2} {a ^ 2} $ $

Außerdem wird $ \ rho $ durch eine Energiedichte ersetzt, die Materie, Strahlung und jede andere Energieform umfasst. Zu Darstellungszwecken wird es jedoch als $ \ rho $ geschrieben.

Weltmodelle für verschiedene Krümmungskonstanten

Betrachten wir nun die verschiedenen Möglichkeiten in Abhängigkeit von den Krümmungskonstantenwerten.

Fall 1: k = 1 oder geschlossenes Universum

Für ein expandierendes Universum ist $ da / dt> 0 $. Wenn die Expansion fortgesetzt wird, lautet der erste Term auf der rechten Seite der obigen Gleichung $ a ^ {- 3} $, während der zweite Term $ a ^ {- 2} $ lautet. Wenn die beiden Terme gleich werden, stoppt das Universum die Expansion. Dann -

$$ \ frac {8 \ pi G} {3} \ rho = \ frac {kc ^ 2} {a ^ 2} $$

Hier ist also k = 1

$$ a = \ left [\ frac {3c ^ 2} {8 \ pi G \ rho} \ right] ^ {\ frac {1} {2}} $$

Ein solches Universum ist endlich und hat ein endliches Volumen. Dies nennt man ein geschlossenes Universum.

Fall 2: k = -1 oder Offenes Universum

Wenn k < 0würde die Expansion niemals aufhören. Nach einiger Zeit kann der erste Term auf der RHS im Vergleich zum zweiten Term vernachlässigt werden.

Hier ist k = -1. Daher ist $ da / dt ∼ c $.

In diesem Fall rollt das Universum aus. Ein solches Universum hat unendlich viel Raum und Zeit. Dies nennt man ein offenes Universum.

Fall 3: k = 0 oder flaches Universum

In diesem Fall dehnt sich das Universum mit abnehmender Geschwindigkeit aus. Hier ist k = 0. Daher ist

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho $$

Ein solches Universum hat unendlich viel Raum und Zeit. Dies nennt man ein flaches Universum.

Punkte, die man sich merken sollte

• Die Friedmann-Gleichung sagt etwas über die Expansion des Raums in homogenen und isotropen Modellen des Universums aus.

• Abhängig von unterschiedlichen Krümmungskonstantenwerten können wir ein geschlossenes, offenes oder flaches Universum haben.

In diesem Kapitel werden wir die Fluidgleichung diskutieren und wie sie uns bezüglich der Dichte des Universums sagt, die sich mit der Zeit ändert.

Schätzung von ρ _c und ρ im gegenwärtigen Universum

Für das gegenwärtige Universum -

$$ \ rho_c \ simeq 10 ^ {11} M_ \ odot M_ {pc} ^ {- 3} \ simeq 10 \: Wasserstoff \: Atome \: m ^ {- 3} $$

In unserem Weltraum gibt es eine ganze Reihe kritischer Dichten. Wie für das intergalaktische Medium ist $ \ rho_c $ 1 Wasserstoffatom $ m ^ {- 3} $, während es für Molekülwolken $ 10 ^ 6 $ Wasserstoffatome $ m ^ {- 3} $ ist.

Wir müssen $ \ rho_c $ unter Berücksichtigung der richtigen Raumproben messen. In unserer Galaxie ist der Wert von $ \ rho_c $ sehr hoch, aber unsere Galaxie ist kein Vertreter des gesamten Universums. Wir sollten also in den Weltraum gehen, in dem das kosmologische Prinzip gilt, dh Entfernungen ≈ 300 Mpc. 300 Mpc zu betrachten bedeutet, 1 Milliarde Jahre zurückzublicken, aber es ist immer noch das gegenwärtige Universum.

Umfragen wie SDSS werden durchgeführt, um die tatsächliche Materiedichte zu bestimmen. Sie nehmen ein Volumen von 5 × 500 × 5 Mpc ^{3 auf} , zählen die Anzahl der Galaxien und fügen das gesamte von diesen Galaxien kommende Licht hinzu. Unter der Annahme, dass 1 L ≡ 1 M, dh 1 Sonnenleuchtkraft ≡ 1 Sonnenmasse.

Wir führen eine Umwandlung von Licht in Masse durch und versuchen dann, die Anzahl der Baryonen basierend auf den in diesem Volumen vorhandenen Partikeln der sichtbaren Materie abzuschätzen.

Zum Beispiel,

$$ 1000L_ \ odot ≡ 1000M_ \ odot / m_p $$

Wobei m _p = Masse des Protons.

Dann erhalten wir ungefähr die Baryonenzahldichte $ \ Omega b ∼ = 0,025 $. Dies impliziert $ \ rho b = 0,25% $ von $ \ rho_c $. Verschiedene Umfragen haben einen etwas anderen Wert ergeben. Im lokalen Universum ist die Zahlendichte der sichtbaren Materie viel geringer als die kritische Dichte, was bedeutet, dass wir in einem offenen Universum leben.

Masse mit einem Faktor von 10 ist in diesen Erhebungen nicht enthalten, da diese Erhebungen elektromagnetische Strahlung, aber keine dunkle Materie berücksichtigen. Geben, $ \ Omega_m = 0,3 - 0,4 $. Kommt immer noch zu dem Schluss, dass wir in einem offenen Universum leben.

Dunkle Materie interagiert mit der Schwerkraft. Viel dunkle Materie kann die Expansion stoppen. Wir haben noch nicht formalisiert, wie sich $ \ rho $ mit der Zeit ändert, wofür wir einen weiteren Satz von Gleichungen benötigen.

Thermodynamik besagt, dass -

$$ dQ = dU + dW $$

Für ein System, das an Größe zunimmt, ist $ dW = P dV $. Die Expansion des Universums wird als adiabatisch modelliert, dh $ dQ = 0 $. Eine Volumenänderung sollte also aufgrund einer Änderung der internen Energie dU erfolgen.

Nehmen wir ein bestimmtes Volumen des Universums mit dem Radius der Einheit, dh $ r_c = 1 $. Wenn $ \ rho $ die Materialdichte innerhalb dieses Raumvolumens ist, dann

$$ M = \ frac {4} {3} \ pi a ^ 3r_c ^ 3 \ rho $$

$$ U = \ frac {4} {3} \ pi a ^ 3 \ rho c ^ 2 $$

Wo, Uist die Energiedichte. Lassen Sie uns die Veränderung der inneren Energie mit der Zeit herausfinden, während sich das Universum ausdehnt.

$$ \ frac {\ mathrm {d} U} {\ mathrm {d} t} = 4 \ pi a ^ 2 \ rho c ^ 2 \ frac {\ mathrm {d} a} {\ mathrm {d} t} + \ frac {4} {3} \ pi a ^ 3 c ^ 2 \ frac {\ mathrm {d} \ rho} {\ mathrm {d} t} $$

In ähnlicher Weise ist die Änderung des Volumens mit der Zeit gegeben durch:

$$ \ frac {\ mathrm {d} V} {\ mathrm {d} t} = 4 \ pi ^ 2 \ frac {\ mathrm {d} a} {\ mathrm {d} t} $$

Ersetzen von $ dU = −P dV $. Wir bekommen,

$$ 4 \ pi a ^ 2 (c ^ 2 \ rho + P) \ dot {a} + \ frac {4} {3} \ pi a ^ 3c ^ 2 \ dot {\ rho} = 0 $$

$$ \ dot {\ rho} +3 \ frac {\ dot {a}} {a} \ left (\ rho + \ frac {P} {c ^ 2} \ right) = 0 $$

Dies nennt man das Fluid Equation. Es zeigt uns, wie sich die Dichte des Universums mit der Zeit ändert.

Der Druck sinkt, wenn sich das Universum ausdehnt. Zu jedem Zeitpunkt ändert sich der Druck, es gibt jedoch keinen Druckunterschied zwischen zwei Punkten des betrachteten Volumens, sodass der Druckgradient Null ist. Nur relativistische Materialien üben Druck aus, Materie ist drucklos.

Die Friedmann-Gleichung modelliert zusammen mit der Fluid-Gleichung das Universum.

Punkte, die man sich merken sollte

• Dunkle Materie interagiert mit der Schwerkraft. Viel dunkle Materie kann die Expansion stoppen.

• Die Flüssigkeitsgleichung zeigt uns, wie sich die Dichte des Universums mit der Zeit ändert.

• Die Friedmann-Gleichung modelliert zusammen mit der Fluid-Gleichung das Universum.

• Nur relativistische Materialien üben Druck aus, Materie ist drucklos.

In diesem Kapitel werden wir die Lösungen für Friedmann-Gleichungen im Zusammenhang mit dem von Materie dominierten Universum diskutieren. In der Kosmologie können wir, weil wir alles in großem Maßstab sehen, die Sonnensysteme, Galaxien, alles wie Staubpartikel (so sehen wir es mit unseren Augen), es staubiges Universum oder nur Materieuniversum nennen.

In dem Fluid Equation,

$$ \ dot {\ rho} = -3 \ left (\ frac {\ dot {a}} {a} \ right) \ rho -3 \ left (\ frac {\ dot {a}} {a} \ right ) \ left (\ frac {P} {c ^ 2} \ right) $$

Wir können sehen, dass es einen Druckbegriff gibt. Für ein staubiges UniversumP = 0, weil die Energiedichte der Materie größer als der Strahlungsdruck ist und sich die Materie nicht mit relativistischer Geschwindigkeit bewegt.

So wird die Fluidgleichung,

$$ \ dot {\ rho} = -3 \ left (\ frac {\ dot {a}} {a} \ right) \ rho $$

$$ \ Rightarrow \ dot {\ rho} a + 3 \ dot {a} \ rho = 0 $$

$$ \ Rightarrow \ frac {1} {a ^ 3} \ frac {\ mathrm {d}} {\ mathrm {d} t} (a ^ 3 \ rho) = 0 $$

$$ \ Rightarrow \ rho a ^ 3 = \: Konstante $$

$$ \ Rightarrow \ rho \ propto \ frac {1} {a ^ 3} $$

In dieser Gleichung gibt es keine Gegenintuition, da die Dichte als $ a ^ {- 3} $ skaliert werden sollte, da das Volumen als $ a ^ 3 $ zunimmt.

Aus der letzten Beziehung können wir sagen, dass

$$ \ frac {\ rho (t)} {\ rho_0} = \ left [\ frac {a_0} {a (t)} \ right] ^ 3 $$

Für das gegenwärtige Universum a, was gleich ist a₀ sollte 1 sein. Also

$$ \ rho (t) = \ frac {\ rho_0} {a ^ 3} $$

In einem von Materie dominierten flachen Universum ist k = 0. Die Friedmann-Gleichung wird also zu:

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G \ rho} {3} $$

$$ \ dot {a} ^ 2 = \ frac {8 \ pi G \ rho a ^ 2} {3} $$

Wenn wir diese Gleichung lösen, erhalten wir:

$$ a \ propto t ^ {2/3} $$

$$ \ frac {a (t)} {a_0} = \ left (\ frac {t} {t_0} \ right) ^ {2/3} $$

$$ a (t) = \ left (\ frac {t} {t_0} \ right) ^ {2/3} $$

Dies bedeutet, dass das Universum mit abnehmender Geschwindigkeit weiter zunimmt. Das folgende Bild zeigt die Expansion eines staubigen Universums.

Wie ρ ändert sich mit der Zeit?

Schauen Sie sich die folgende Gleichung an:

$$ \ frac {\ rho (t)} {\ rho_0} = \ left (\ frac {t_0} {t} \ right) ^ 2 $$

Wir wissen, dass sich der Skalierungsfaktor mit der Zeit als $ t ^ {2/3} $ ändert. Damit,

$$ a (t) = \ left (\ frac {t} {t_0} \ right) ^ {2/3} $$

Wenn wir es differenzieren, werden wir bekommen,

$$ \ frac {(da)} {dt} = \ dot {a} = \ frac {2} {3} \ left (\ frac {t ^ {- 1/3}} {t_0} \ right) $$

Wir wissen, dass die Hubble Constant ist,

$$ H (t) = \ frac {\ dot {a}} {a} = \ frac {2} {3t} $$

Dies ist die Gleichung für Einstein-de sitter Universe. Wenn wir das gegenwärtige Alter des Universums berechnen wollen, dann

$$ t_0 = t_ {age} = \ frac {2} {3H_0} $$

Nachdem wir den Wert von $ H_0 $ für das gegenwärtige Universum eingegeben haben, erhalten wir den Wert des Alters des Universums als 9 Gyrs. Es gibt vieleGlobular Cluster in unserer eigenen Milchstraße, die mehr Alter hat.

Das war alles über das staubige Universum. Wenn Sie nun annehmen, dass das Universum von Strahlung und nicht von Materie dominiert wird, lautet die Strahlungsenergiedichte $ a ^ {- 4} $ und nicht $ a ^ {- 3} $. Wir werden mehr davon im nächsten Kapitel sehen.

Punkte, die man sich merken sollte

• In der Kosmologie ist alles wie Staubpartikel, daher nennen wir es staubiges Universum oder nur Materieuniversum.

• Wenn wir annehmen, dass das Universum von Strahlung und nicht von Materie dominiert wird, lautet die Strahlungsenergiedichte $ a ^ {- 4} $ und nicht $ a ^ {- 3} $.

In diesem Kapitel werden wir die Lösungen für Friedmann-Gleichungen im Zusammenhang mit dem strahlungsdominierten Universum diskutieren. Am Anfang vergleichen wir die Energiedichte der Materie mit der der Strahlung. Auf diese Weise können wir sehen, ob unser Universum von Materie oder Strahlung dominiert wird.

Energiedichte der Strahlung

Die im gegenwärtigen Universum vorherrschende Strahlung kann den Sternquellen nur sehr wenig zugeschrieben werden, ist jedoch hauptsächlich auf den verbleibenden CMB (Cosmic Microwave Background) zurückzuführen.

Die Energiedichte der Strahlung $ \ epsilon _ {\ gamma, 0} $ kann wie folgt ausgedrückt werden:

$$ \ epsilon _ {\ gamma, 0} = aT_0 ^ 4 $$

Hier, a ist die Strahlungskonstante, deren Ausdruck $ (8 \ pi ^ 5k_B ^ 4) / (15h ^ 3c ^ 2) $ gleich ist a = 7.5657 × 10⁻¹⁵erg\: cm⁻³ K⁻⁴. Die Temperatur T0, die wir hier betrachten, entspricht der des schwarzen Körpers, der dem CMB entspricht.

Wir haben die Ergebnisse ersetzt,

$$ \ epsilon _ {\ gamma, 0} = aT_0 ^ 4 = 4 \ mal 10 ^ {- 13} erg \: cm ^ {- 3} $$

Energiedichte der Materie

In den folgenden Berechnungen gehen wir davon aus, mit einem flachen Universum und K = 0 zu arbeiten. Wir betrachten die Energiedichte der Materie als $ \ epsilon = \ rho c ^ 2 $. Wir betrachten Folgendes:

$$ \ rho_ {m, 0} c ^ 2 = 0,3 \ rho_ {c, 0} c ^ 2 = 0,3 \ times \ frac {3H_0 ^ 2} {8 \ pi G} \ times c ^ 2 $$

$$ \ rho_ {m, 0} c ^ 2 \ simeq 2 \ times 10 ^ {- 8} erg \: cm ^ {- 3} $$

$$ \ rho_ {b, 0} c ^ 2 = 0,03 \ rho_ {c, 0} c ^ 2 = 0,03 \ times \ frac {3H_0 ^ 2} {8 \ pi G} \ times c ^ 2 $$

$$ \ rho_ {b, 0} c ^ 2 \ simeq 2 \ times 10 ^ {- 9} erg \: cm ^ {- 3} $$

Aus der obigen Berechnung geht hervor, dass wir in einem von Materie dominierten Universum leben. Dies kann durch die Tatsache unterstützt werden, dass der CMB sehr kalt ist. Wenn wir in die Vergangenheit zurückblicken, wird die CMB-Temperatur immer heißer und wir können daraus schließen, dass es eine Epoche gegeben haben könnte, in der das Universum von Strahlung dominiert wurde.

Variation von Dichte und Skalierungsfaktor

Die Flüssigkeitsgleichung zeigt uns, dass -

$$ \ dot {\ rho} + 3 \ frac {\ dot {a}} {a} \ left (\ rho + \ frac {P} {c ^ 2} \ right) = 0 $$

Wenn wir ein staubiges Universum betrachten, hätten wir P = 0. Abgesehen von den vorherigen Ergebnissen betrachten wir das Universum als von Strahlung dominiert.

$$ \ dot {\ rho} _ {rad} + 3 \ frac {\ dot {a}} {a} \ left (\ rho_ {rad} + \ frac {P} {c ^ 2} \ right) = 0 $$

Unter Verwendung der Druckrelation von $ P_ {rad} = \ rho c ^ {2/3} $ haben wir -

$$ \ dot {\ rho} _ {rad} + 3 \ frac {\ dot {a}} {a} \ left (\ rho_ {rad} + \ frac {\ rho_ {rad}} {3} \ right) = 0 $$

$$ \ dot {\ rho} _ {rad} + 4 \ frac {\ dot {a}} {a} (\ rho_ {rad}) = 0 $$

Bei weiterer Vereinfachung haben wir:

$$ \ frac {1} {a ^ 4} \ frac {\ mathrm {d}} {\ mathrm {d} t} (\ rho_ {rad} a ^ 4) = 0 $$

$$ \ rho_ {rad} a ^ 4 = \: Konstante $$

$$ \ rho_ {rad} \ propto \ frac {1} {a ^ 4} $$

Das obige Ergebnis zeigt eine inverse 4. ^{Potenzvariation} von a mit $ \ rho $.

Dies kann physikalisch als $ a ^ {- 3} $ interpretiert werden, das sich aus der Variation des Volumens ergibt, wenn es zunimmt. Die verbleibenden $ a ^ {- 1} $ können als die Energie behandelt werden, die das Photon aufgrund der Ausdehnung des Raums im Universum verliert (kosmologische Rotverschiebung 1 + z = a ^-1 ).

Das folgende Bild zeigt die zeitliche Veränderung von Materie und Strahlungsdichte.

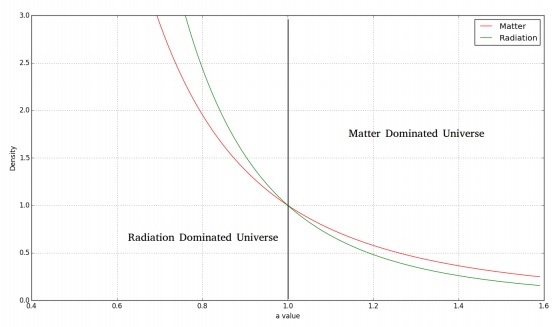
Für ein flaches, strahlungsdominiertes Universum hätten wir die Friedmann-Gleichung wie folgt:

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G \ rho} {3} $$

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ frac {\ rho_0} {a ^ 4} $$

Zur Vereinfachung und Anwendung der Lösung auf die Differentialgleichung haben wir -

$$ (\ dot {a}) ^ 2 = \ frac {8 \ pi G \ rho_0} {3a ^ 2} $$

$$ \ Rightarrow a (t) \ propto t ^ {\ frac {1} {2}} $$

So haben wir -

$$ a (t) = a_0 \ left (\ frac {t} {t_0} \ right) ^ {\ frac {1} {2}} $$

Aus der obigen Gleichung sehen wir, dass die Anstiegsrate des Skalierungsfaktors kleiner ist als die des staubigen Universums.

Punkte, die man sich merken sollte

• Die im gegenwärtigen Universum vorherrschende Strahlung kann den Sternquellen nur sehr wenig zugeschrieben werden.

• Für ein staubiges Universum ist der Druck Null.

• CMB ist sehr kalt.

Das Gebiet der Dunklen Energie ist in der Astronomie ein sehr graues Gebiet, da es in allen Gleichungen ein freier Parameter ist, aber es gibt keine klare Vorstellung davon, was genau dies ist.

Wir werden mit den Friedmannschen Gleichungen beginnen,

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho - \ frac {k \ ast c ^ 2} {a ^ 2} $$

Die meisten elementaren Bücher über Kosmologie beginnen mit der Beschreibung der dunklen Energie aus dieser Episode, dass das Universum vor Hubbles Beobachtung geschlossen und statisch ist.

Damit das Universum auf der rechten Seite statisch ist, sollten beide Terme übereinstimmen und Null sein. Wenn der erste Term jedoch größer als der zweite Term ist, ist das Universum nicht statisch, sodass Einstein den freien Parameter fallen ließ ∧ in die Feldgleichung, um das Universum statisch zu machen, so argumentierte er, dass unabhängig davon, was der erste Term mit dem zweiten Term verglichen wird, man immer ein statisches Universum erhalten kann, wenn es eine weitere Komponente in der Gleichung gibt, die die Störung kompensieren kann Übereinstimmung zwischen diesen beiden Begriffen.

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho - \ frac {k \ ast c ^ 2} {a ^ 2} + \ frac {\ wedge} {3} $$

$$ \ left (\ frac {\ ddot {a}} {a} \ right) = - \ frac {4 \ pi G} {3} \ left (\ rho + \ frac {3P} {c ^ 2} \ rechts) + \ frac {\ wedge} {3} $$

Wobei $ P = \ rho \ ast c ^ 2/3 $ und $ \ wedge = \ rho \ ast c ^ 2 $ der kosmologische Parameter ist. (Negatives Vorzeichen ist nur wegen der Anziehung)

In der obigen Gleichung (Beschleunigungsgleichung) -

• $ 3P / c ^ 2 $ ist der Unterdruck aufgrund von Strahlung,

• $ -4 \ pi G / 3 $ ist die Anziehungskraft aufgrund der Schwerkraft und

• $ \ wedge / 3 $ leistet einen positiven Beitrag.

Der dritte Term wirkt als Abstoßungskraft, weil ein anderer Teil der Gleichung attraktiv ist.

Die physikalische Bedeutung der Gleichung ist die folgende ˙a = 0weil es keine Beweise gab, die zeigen, dass sich das Universum ausdehnt. Was ist, wenn diese beiden Begriffe nicht miteinander übereinstimmen? Es ist daher besser, eine Komponente hinzuzufügen, und je nach Versatz können wir den Wert des freien Parameters jederzeit ändern.

Zu dieser Zeit gab es keine physikalische Erklärung für diese kosmologischen Parameter, weshalb, als die Erklärung des expandierenden Universums in den 1920er Jahren entdeckt wurde, wo Einstein musste sofort diese Konstante rauswerfen.

Die Erklärung dafür cosmological constant wird immer noch verwendet, weil es eine andere Version des Universums erklärt, aber die Definition dieser kosmologischen Konstante, die Art der Interpretation, änderte sich mit der Zeit.

Nun wurde das Konzept dieser kosmologischen Konstante aus vielen Gründen auf die Kosmologie zurückgeführt. Einer der Gründe ist, dass wir Beobachtungen zur Energiedichte verschiedener Komponenten des Universums (Baryon, Dunkle Materie, Strahlung) haben, sodass wir wissen, was dieser Parameter ist. Unabhängige Beobachtungen mitcosmic microwave background zeigt, dass k = 0 ist.

$$ CMB, k = 0 \: \ rho = \ rho_c = \ frac {3H_0 ^ 2} {8 \ pi G} \ ca. 10 \: Wasserstoff \: Atome.m ^ {- 3} $$

Damit k 0 ist, sollte $ \ rho $ gleich $ \ rho_c $ sein, aber alles, was wir wissen, wenn wir es addieren, ergibt nicht 0, was bedeutet, dass es eine andere Komponente gibt, die zeigt, dass es viel kleiner als ist $ \ rho_c $.

$$ \ rho = \ rho_b + \ rho_ {DM} + \ rho_ {rad} << \ rho_c $$

Ein weiterer Beweis für dunkle Energie kommt von der Type 1 Supernova ObservationDies tritt auf, wenn der Weiße Zwerg die Materie anreichert und die Chandrashekhar-Grenze überschreitet, die eine sehr genaue Grenze ist (≈ 1,4 M). Jedes Mal, wenn eine Supernova-Explosion vom Typ 1 auftritt, haben wir dieselbe Masse, was bedeutet, dass die gesamte Bindungsenergie des Systems gleich ist und die Menge an Lichtenergie, die wir sehen können, gleich ist.

Natürlich nimmt das Supernova-Licht zu und fällt dann in Ohnmacht, aber wenn Sie die Spitzenhelligkeit messen, wird es immer gleich sein, was es zu einem Standardkandidaten macht. Mit einer Supernova vom Typ 1 haben wir die kosmologische Komponente des Universums gemessen, und Astronomen stellten fest, dass die Supernova mit hoher Rotverschiebung 30% - 40% schwächer ist als die Supernova mit niedriger Rotverschiebung, und es kann erklärt werden, ob es keine gibt -Null∧ Begriff.

In kosmologischen Modellen DE (Dark Energy)wird als Flüssigkeit behandelt, was bedeutet, dass wir die Zustandsgleichung dafür schreiben können. Die Zustandsgleichung ist die Gleichung, die die Variablen wie Druck, Dichte, Temperatur und Volumen zweier verschiedener Zustände der Materie verbindet.

Dimensional sehen wir,

$$ \ frac {8 \ pi G} {3} \ rho = \ frac {\ wedge} {3} $$

$$ \ rho_ \ wedge = \ frac {\ wedge} {8 \ pi G} $$

Energiedichte von DE,

$$ \ epsilon_ \ wedge = \ rho_ \ wedge \ ast c ^ 2 = \ frac {\ wedge c ^ 2} {8 \ pi G} $$

Dunkler Energiedichteparameter,

$$ \ Omega_ \ wedge = \ frac {\ rho_ \ wedge} {\ rho_c} $$

$ \ Omega_ \ wedge $ ist die Dichte der dunklen Energie in Bezug auf die kritische Dichte.

$$ \ rho = \ rho_b + \ rho_ {DM} + \ rho_ \ wedge $$

Es gibt eine Reihe von Theorien über dunkle Energie, die das Universum abstoßen und dazu führen, dass sich das Universum ausdehnt. Eine Hypothese ist, dass diese dunkle Energie eine Vakuumenergiedichte sein könnte. Angenommen, der Raum selbst verarbeitet etwas Energie, und wenn Sie die Menge an baryonischer Materie, dunkler Materie und der Strahlung innerhalb des Raumvolumens zählen, zählen Sie auch die Energiemenge, die mit dem Raum verbunden ist, aber es ist nicht klar dass die dunkle Energie wirklich eine Vakuumenergiedichte ist.

Wir wissen, dass die Beziehung zwischen Dichte und Skalierungsfaktor für dunkle Materie und Strahlung ist,

$$ \ rho_m \ propto \ frac {1} {a ^ 3} $$

$$ \ rho_m \ propto \ frac {1} {a ^ 4} $$

Wir haben das Diagramm des Dichte-V / S-Skalierungsfaktors. In derselben Darstellung können wir sehen, dass $ \ rho_ \ wedge $ eine Konstante mit der Expansion des Universums ist, die nicht vom Skalierungsfaktor abhängt.

Das folgende Bild zeigt die Beziehung zwischen Dichte und Skalierungsfaktor.

‘ρ’ v/s ‘a’(Skalierungsfaktor, der sich auf die Zeit bezieht) In demselben Diagramm wird die Dunkle Energie als Konstante modelliert. Was auch immer dunkle Energie wir im gegenwärtigen Universum messen, es ist eine Konstante.

Punkte, die man sich merken sollte

• Unabhängige Beobachtungen unter Verwendung des kosmischen Mikrowellenhintergrunds zeigen, dass k = 0 ist.

• $ \ rho_ \ wedge $ ist eine Konstante mit der Expansion des Universums, die nicht vom Skalierungsfaktor abhängt.

• Die Schwerkraft ändert sich auch mit der Zeit, die genannt wird modified Newtonian dynamics.

In diesem Kapitel werden wir uns mit Rotationskurven von Spiralgalaxien und Beweisen für Dunkle Materie befassen.

Dunkle Materie und Beobachtungsfaktor über Dunkle Materie

• Der frühe Beweis der Dunklen Materie war der study of the Kinematics of Spiral Galaxy.

• Die Sonne ist 30.000 Lichtjahre vom Zentrum unserer Galaxie entfernt. Die galaktische Zentriergeschwindigkeit beträgt 220 km / s.

• Warum ist die Geschwindigkeit 220 km / s nicht 100 km / s oder 500 km / s? Was regelt die Kreisbewegung des Objekts?

• Die im Radius eingeschlossene Masse hilft, die Geschwindigkeit im Universum zu erfassen.

Rotation der Milchstraße oder der Spiralgalaxie - Differenzielle Rotation

• Angular Velocity variiert mit dem Abstand vom Zentrum.

• Die Umlaufzeit hängt von der Entfernung vom Zentrum ab.

• Material, das näher am galaktischen Zentrum liegt, hat einen kürzeren Zeitraum und Material, das weit vom galaktischen Zentrum entfernt ist, hat einen größeren Zeitraum.

Rotationskurve

• Sagen Sie die Geschwindigkeitsänderung mit dem voraus Galactic centric radius. Die Kurve, die die Geschwindigkeit angibt, ändert sich mit dem Umlaufradius.

• Wenn wir sehen, wie sich Dinge bewegen, denken wir, dass es die Schwerkraft ist, die die Rotation beeinflusst.

• Die Massenverteilung variiert mit dem Radius. Die Materiedichte sagt die Rotationskurve voraus. Die Rotationskurve basiert auf der Materiedichte, die mit dem Radius variiert.

Oberflächenhelligkeit

• Wir wählen den Patch und sehen, wie viel Licht herauskommt.

• Die Menge des vom Patch kommenden Lichts wird als Oberflächenhelligkeit bezeichnet.

• Seine Einheit ist mag/arcsec².

• Wenn wir feststellen, dass die Oberflächenhelligkeit mit dem Radius variiert, können wir feststellen, dass die Leuchtmasse mit dem Radius variiert.

  $$ \ mu (r) \ propto exp \ left (\ frac {-r} {h_R} \ right) $$

  $ h_R $ ist die Skalenlänge. $ \ mu (r) = \ mu_o \ ast exp \ left (\ frac {-r} {h_R} \ right) $

• $ h_R $ ist fast 3 kpc für die Milchstraße.

Spiralgalaxien

Damit die Astronomen die Rotationskurve verstehen können, teilen sie die Galaxien in zwei Komponenten auf:

• Disk
• Bulge

Das folgende Bild zeigt eine zentrale Kugelwölbung + Kreisscheibe. Die Stern- und Gasverteilung ist in der Ausbuchtung und der Scheibe unterschiedlich.

Kinematik von Spiralgalaxien

• Die Kreisgeschwindigkeit eines beliebigen Objekts - Für die Ausbuchtung ist (r <Rb).

  $$ V ^ 2 (r) = G \ ast \ frac {M (r)} {r} $$

  $$ M (r) = \ frac {4 \ pi r ^ 3} {3} \ ast \ rho_b $$

• Für die Platte - (Rb <r <Rd)

  $$ V ^ 2 (r) = G \ ast \ frac {M (r)} {r} $$

• Die Ausbuchtung hat eine ungefähr konstante Dichte an Sternen.

• Die Dichte innerhalb der Ausbuchtung ist konstant (ändert sich nicht mit dem Abstand innerhalb der Ausbuchtung).

• In einer Scheibe nimmt die Sternendichte mit dem Radius ab. Der Radius nimmt zu, dann nimmt die Leuchtmasse ab.

• In loser Schüttung - $ V (r) \ propto r $

• In Disc - $ V (r) \ propto 1 / \ sqrt {r} $

Rotationskurve von Spiralgalaxien

• Durch die Spectroscopy (nahe Galaxien - räumlich aufgelöste Galaxie), erzeugen wir die Rotationskurve.

• Wie oben erwähnt, sehen wir, dass die Rotationskurve in den äußeren Bereichen flach ist, dh die Dinge bewegen sich in den äußeren Bereichen schnell, was im Allgemeinen nicht in dieser Form erwartet wird.

• Die Umlaufgeschwindigkeit nimmt mit zunehmendem Radius des inneren Bereichs zu, flacht jedoch im äußeren Bereich ab.

Dunkle Materie

Die Dunkle Materie soll die nicht leuchtende Komponente des Universums sein. Lassen Sie uns die Dunkle Materie anhand der folgenden Hinweise verstehen.

• Die flachen Rotationskurven stehen im Widerspruch zu dem, was wir für die Verteilung von Sternen und Gas in den Spiralgalaxien sehen.

• Die Oberflächenhelligkeit der Scheibe nimmt mit dem Radius exponentiell ab, was bedeutet, dass sich die Masse der Leuchtmasse, hauptsächlich Sterne, um das galaktische Zentrum konzentriert.

• Die Abflachung der Rotationskurve legt nahe, dass sich die Gesamtmasse der Galaxie innerhalb eines Radius befindet r nimmt immer mit der Zunahme zu r.

• Dies kann nur erklärt werden, wenn sich in diesen Galaxien eine große Menge unsichtbarer Gravitationsmasse befindet, die keine elektromagnetische Strahlung abgibt.

• Die Rotationskurvenmessungen von Spiralgalaxien sind einer der überzeugendsten Beweise für dunkle Materie.

Beweise der Dunklen Materie

• Fehlende Masse - 10-fache Leuchtmasse.

• Der größte Teil dieser dunklen Materie muss sich im Lichthof der Galaxie befinden: Große Mengen dunkler Materie in der Scheibe können die Langzeitstabilität der Scheibe gegen Gezeitenkräfte stören.

• Ein kleiner Teil der dunklen Materie in der Scheibe kann baryonisch-dunkle Sterne (braune Zwerge, schwarze Zwerge) und kompakte Sternreste (Neutronensterne, schwarze Löcher) sein. Eine solche baryonische dunkle Materie kann jedoch nicht das volle Ausmaß der fehlenden Masse in Galaxien erklären.

• Dichteprofil der Dunklen Materie - $ M (r) \ propto r $ und $ \ rho (r) \ propto r ^ {- 2} $.

• Die Rotationskurvendaten für Spiralgalaxien stimmen mit der in ihrem Lichthof verteilten dunklen Materie überein.

• Dieser dunkle Heiligenschein macht einen Großteil der Gesamtmasse der Galaxie aus.

• Alle baryonischen Materien (Sterne, Sternhaufen, ISM usw.) werden durch das Gravitationspotential dieses Halos der dunklen Materie zusammengehalten.

Fazit

• Dunkle Materie wurde nur durch ihre Gravitationswechselwirkung mit einer gewöhnlichen Materie nachgewiesen. Es wurde noch keine Wechselwirkung mit Licht (keine elektromagnetische Kraft) beobachtet.

• Neutrinos- Laden Sie weniger auf, interagieren Sie schwach, aber die Masse ist zu gering (<0,23 eV). DM-Partikel sollten etwa E> 10 eV haben, um die Strukturbildung zu erklären.

• Schwach wechselwirkende massive Teilchen (WIMPS) können die Quelle der Dunklen Materie sein.

Punkte, die man sich merken sollte

• Material, das näher am galaktischen Zentrum liegt, hat einen kürzeren Zeitraum.

• Die Ausbuchtung hat eine ungefähr konstante Dichte an Sternen.

• Die Oberflächenhelligkeit der Scheibe nimmt mit dem Radius exponentiell ab.

• Große Mengen dunkler Materie in der Scheibe können die Langzeitstabilität der Scheibe gegen Gezeitenkräfte stören.

Erste direkte Beweise für dunkle Materie kamen von Frids Ricky. Er machte einige Beobachtungen, die zum ersten Mal dunkle Materie enthüllten. Seine Beobachtungen berücksichtigten die Gesamtbewegung innerhalb des Galaxienhaufens.

Erweiterte Objekte sind Galaxienhaufen und werden als gebundene Strukturen betrachtet. Diese Galaxien bewegen sich in Bezug auf das Clusterzentrum, fliegen aber nicht ab. Wir betrachten die Gesamtbewegung der Galaxie.

Annahme: Geschwindigkeiten repräsentieren das zugrunde liegende Potenzial

Jede Galaxie hat ihre eigene Eigenbewegung innerhalb des Clusters und Hubble Flow Component. Die kleineren Galaxien sind kleiner, der größte Teil des Lichts kommt von M31 und MW, es gibt mehrere Zwerggalaxien. Für unsere Rohanalyse können wir nur M31 und MW verwenden und die dynamische Masse der lokalen Gruppe bewerten.

Es gibt eine Relativgeschwindigkeit zwischen uns und M31. Es ist grob, aber es ist wahr. Die Geschichte beginnt vor langer Zeit, als M31 und MW nahe beieinander waren, weil sie Mitglieder eines Clusters waren, das sie voneinander entfernten. Nach einiger Zeit erreichen sie die maximale Trennung und kommen sich dann näher.

Nehmen wir an, dass die maximale Trennung, die jemals erreicht werden kann, $ r_ {max} $ ist. Jetzt haben sie eine Trennung namensr. LassenMsei die kombinierte Masse von MW und M31. Wir wissen nicht, wann $ r_ {max} $ erreicht ist.

$$ \ frac {GM} {r_ {max}} = \: Potential \: at \: r_ {max} $$

Wenn diese Galaxien zu einem bestimmten Zeitpunkt nahe beieinander kamen, wird die Energie des Systems -

$$ \ frac {1} {2} \ sigma ^ 2 = \ frac {GM} {r} = \ frac {GM} {r_ {max}} $$

σ ist die Relativgeschwindigkeit beider Galaxien. M ist nur eine reduzierte Masse, aber die Testmasse ist 1. σ ist die Geschwindigkeit eines Objekts in der Entfernung rvon der Mitte des Clusters. Wir glauben, dass dieser Cluster in einer dynamischen Gleichung vorliegt, da der Virialsatz gilt. Galaxien können also nicht mit unterschiedlicher Geschwindigkeit kommen.

Wie viel Zeit würden diese Galaxien brauchen, um die maximale Entfernung zu erreichen?

Um dies zu verstehen, betrachten wir die folgende Gleichung.

$$ \ frac {1} {2} \ left (\ frac {dr} {dt} \ right) ^ 2 = \ frac {GM} {r} - \ frac {GM} {r_ {max}} $$

$$ t_ {max} = \ int_ {0} ^ {r_ {max}} dt = \ int_ {0} ^ {r_ {max}} \ frac {dr} {\ sqrt {2GM}} \ left (\ frac {1} {r} - \ frac {1} {r_ {max}} \ right) ^ 2 $$

$$ t_ {max} = \ frac {\ pi r_ {max} ^ {\ frac {3} {2}}} {2 \ sqrt {2GM}} $$

Wobei M = dynamische Masse der lokalen Gruppe. Die Gesamtzeit vom Beginn bis zum Ende der Kollision beträgt $ 2t_ {max} $. Deshalb,

$$ 2t_ {max} = t_0 + \ frac {D} {\ sigma} $$

Und $ t_0 $ ist das gegenwärtige Zeitalter des Universums.

Wenn tatsächlich $ t_ {max} <RHS $ ist, haben wir eine Untergrenze für die Zeit. $ D / \ sigma $ ist die Zeit, in der sie erneut kollidieren. Hier haben wir angenommen, dass σ konstant ist.

$$ t_ {max} = \ frac {t_0} {2} + \ frac {D} {2 \ sigma} $$

$$ r_ {max} = t_ {max} \ times \ sigma = 770K_ {pc} $$

Hier ist σ = Relativgeschwindigkeit zwischen MW und M31.

$$ M_ {dynamic} = 3 \ times 10 ^ {12} M_0 $$

$$ M_ {MW} ^ {lum} = 3 \ mal 10 ^ {10} M_0 $$

$$ M_ {M31} ^ {lum} = 3 \ times 10 ^ {10} M_0 $$

In der Praxis wird die dynamische Masse jedoch unter Berücksichtigung jeder Galaxie innerhalb des Clusters ermittelt. Die fehlende Masse ist die dunkle Materie undFrids Rickybemerkte, dass sich die Galaxien im Koma-Cluster zu schnell bewegen. Er sagte die Existenz von Neutronensternen im Jahr nach der Entdeckung von Neutronensternen voraus und benutzte das Palomar-Teleskop, um die Supernova zu finden.

Punkte, die man sich merken sollte

• Erste direkte Beweise für dunkle Materie kamen von Frids Ricky.

• Erweiterte Objekte sind Galaxienhaufen und werden berücksichtigt bound structures.

• Dynamic mass wird unter Berücksichtigung jeder Galaxie innerhalb des Clusters herausgefunden.

In diesem Kapitel werden wir die Parameter Density und Hubble diskutieren.

Hubble-Parameter

Der Hubble-Parameter ist wie folgt definiert:

$$ H (t) \ equiv \ frac {da / dt} {a} $$

Hiermit wird gemessen, wie schnell sich der Skalierungsfaktor ändert. Allgemeiner wird die Entwicklung des Skalierungsfaktors durch die Friedmann-Gleichung bestimmt.

$$ H ^ 2 (t) \ equiv \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho - \ frac {kc ^ 2} {a ^ 2} + \ frac {\ wedge} {3} $$

wo, ∧ ist eine kosmologische Konstante.

Für ein flaches Universum ist k = 0, daher wird die Friedmann-Gleichung -

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho + \ frac {\ wedge} {3} $$

Für ein von Materie dominiertes Universum variiert die Dichte als -

$$ \ frac {\ rho_m} {\ rho_ {m, 0}} = \ left (\ frac {a_0} {a} \ right) ^ 3 \ Rightarrow \ rho_m = \ rho_ {m, 0} a ^ {- 3} $$

und für ein strahlungsdominiertes Universum variiert die Dichte als -

$$ \ frac {\ rho_ {rad}} {\ rho_ {rad, 0}} = \ left (\ frac {a_0} {a} \ right) ^ 4 \ Rightarrow \ rho_ {rad} = \ rho_ {rad, 0} a ^ {- 4} $$

Gegenwärtig leben wir in einem von Materie dominierten Universum. Wenn wir also $ \ rho ≡ \ rho_m $ betrachten, erhalten wir -

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho_ {m, 0} a ^ {- 3} + \ frac {\ wedge} {3} $$

Die kosmologische Konstante und die Dunkle Energiedichte hängen wie folgt zusammen:

$$ \ rho_ \ wedge = \ frac {\ wedge} {8 \ pi G} \ Rightarrow \ wedge = 8 \ pi G \ rho_ \ wedge $$

Daraus erhalten wir -

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho_ {m, 0} a ^ {- 3} + \ frac {8 \ pi G} {3} \ rho_ \ wedge $$

Auch die kritische Dichte und die Hubble-Konstante hängen wie folgt zusammen:

$$ \ rho_ {c, 0} = \ frac {3H_0 ^ 2} {8 \ pi G} \ Rightarrow \ frac {8 \ pi G} {3} = \ frac {H_0 ^ 2} {\ rho_ {c, 0}} $$

Daraus erhalten wir -

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {H_0 ^ 2} {\ rho_ {c, 0}} \ rho_ {m, 0} a ^ {- 3} + \ frac {H_0 ^ 2} {\ rho_ {c, 0}} \ rho_ \ wedge $$

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = H_0 ^ 2 \ Omega_ {m, 0} a ^ {- 3} + H_0 ^ 2 \ Omega _ {\ wedge, 0 } $$

$$ (\ dot {a}) ^ 2 = H_0 ^ 2 \ Omega_ {m, 0} a ^ {- 1} + H_0 ^ 2 \ Omega _ {\ wedge, 0} a ^ 2 $$

$$ \ left (\ frac {\ dot {a}} {H_0} \ right) ^ 2 = \ Omega_ {m, 0} \ frac {1} {a} + \ Omega _ {\ wedge, 0} a ^ 2 $$

$$ \ left (\ frac {\ dot {a}} {H_0} \ right) ^ 2 = \ Omega_ {m, 0} (1 + z) + \ Omega _ {\ wedge, 0} \ frac {1} { (1 + z) ^ 2} $$

$$ \ left (\ frac {\ dot {a}} {H_0} \ right) ^ 2 (1 + z) ^ 2 = \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega _ {\ wedge , 0} $$

$$ \ left (\ frac {\ dot {a}} {H_0} \ right) ^ 2 \ frac {1} {a ^ 2} = \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega_ {\ wedge, 0} $$

$$ \ left (\ frac {H (z)} {H_0} \ right) ^ 2 = \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega _ {\ wedge, 0} $$

Hier ist $ H (z) $ der rotverschiebungsabhängige Hubble-Parameter. Dies kann geändert werden, um den Strahlungsdichteparameter $ \ Omega_ {rad} $ und den Krümmungsdichteparameter $ \ Omega_k $ einzuschließen. Die modifizierte Gleichung lautet -

$$ \ left (\ frac {H (z)} {H_0} \ right) ^ 2 = \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega_ {rad, 0} (1 + z) ^ 4+ \ Omega_ {k, 0} (1 + z) ^ 2 + \ Omega _ {\ wedge, 0} $$

$$ Oder \: \ left (\ frac {H (z)} {H_0} \ right) ^ 2 = E (z) $$

$$ Oder \: H (z) = H_0E (z) ^ {\ frac {1} {2}} $$

wo,

$$ E (z) \ äquiv \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega_ {rad, 0} (1 + z) ^ 4 + \ Omega_ {k, 0} (1 + z) ^ 2 + \ Omega _ {\ wedge, 0} $$

Dies zeigt, dass der Hubble-Parameter mit der Zeit variiert.

Für die Einstein-de Sitter Universum, $ \ Omega_m = 1, \ Omega_ \ wedge = 0, k = 0 $.

Wenn wir diese Werte eingeben, erhalten wir -

$$ H (z) = H_0 (1 + z) ^ {\ frac {3} {2}} $$

Dies zeigt die zeitliche Entwicklung des Hubble-Parameters für das Einstein-de-Sitter-Universum.

Dichteparameter

Der Dichteparameter $ \ Omega $ ist definiert als das Verhältnis der tatsächlichen (oder beobachteten) Dichte ρ zur kritischen Dichte $ \ rho_c $. Für jede Größe $ x $ des entsprechenden Dichteparameters kann $ \ Omega_x $ mathematisch ausgedrückt werden als -

$$ \ Omega_x = \ frac {\ rho_x} {\ rho_c} $$

Für verschiedene betrachtete Größen können wir die folgenden Dichteparameter definieren.

S.No.	Menge	Dichteparameter
1	Baryonen	$ \ Omega_b = \ frac {\ rho_b} {\ rho_c} $
2	Materie (Baryonisch + Dunkel)	$ \ Omega_m = \ frac {\ rho_m} {\ rho_c} $
3	Dunkle Energie	$ \ Omega_ \ wedge = \ frac {\ rho_ \ wedge} {\ rho_c} $
4	Strahlung	$ \ Omega_ {rad} = \ frac {\ rho_ {rad}} {\ rho_c} $

Wo die Symbole ihre übliche Bedeutung haben.

Punkte, die man sich merken sollte

• Die Entwicklung des Skalierungsfaktors wird durch die Friedmann Equation.

• H(z) ist der rotverschiebungsabhängige Hubble-Parameter.

• Das Hubble Parameter variiert mit der Zeit.

• Das Density Parameter ist definiert als das Verhältnis der tatsächlichen (oder beobachteten) Dichte zur kritischen Dichte.

Wie in den früheren Kapiteln erläutert, ist die zeitliche Entwicklung des Hubble-Parameters gegeben durch -

$$ H (z) = H_0E (z) ^ {\ frac {1} {2}} $$

Wo z ist die Rotverschiebung und E(Z) ist -

$$ E (z) \ äquiv \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega (1 + z) ^ 4 + \ Omega_ {k, 0} (1 + z) ^ 2 + \ Omega ^ {\ wedge, 0} $$

Wenn die Expansion des Universums konstant ist, wird das wahre Alter des Universums wie folgt angegeben:

$$ t_H = \ frac {1} {H_0} $$

Wenn es sich um das von Materie dominierte Universum handelt, dh um das Einstein-Desitter-Universum, dann ist das wahre Zeitalter des Universums gegeben durch -

$$ t_H = \ frac {2} {3H_0} $$

Skalierung und Rotverschiebung wird definiert durch -

$$ a = \ frac {a_0} {1 + z} $$

Das Alter des Universums in Bezug auf den kosmologischen Parameter wird wie folgt abgeleitet.

Der Hubble-Parameter ist gegeben durch -

$$ H = \ frac {\ frac {da} {dt}} {a} $$

Differenzieren bekommen wir -

$$ da = \ frac {-dz} {(1 + z) ^ 2} $$

Wo a₀ = 1 (Barwert des Skalierungsfaktors)

$$ \ frac {\ mathrm {d} a} {\ mathrm {d} t} = \ frac {-1} {(1 + z) ^ 2} $$

$$ \ frac {\ mathrm {d} a} {\ mathrm {d} t} = \ frac {\ mathrm {d} a} {\ mathrm {d} t} \ frac {\ mathrm {d} z} { \ mathrm {d} t} $$

$$ H = \ frac {\ dot {a}} {a} = \ frac {\ mathrm {d} a} {\ mathrm {d} t} \ frac {\ mathrm {d} z} {\ mathrm {d } t} \ frac {1 + z} {1} $$

$$ \ frac {\ dot {a}} {a} = \ frac {-1} {1 + z} \ frac {\ mathrm {d} z} {\ mathrm {d} t} \ frac {1} { 1} $$

$$ H (z) = H_0E (z) ^ {\ frac {1} {2}} $$

$$ dt = \ frac {-dz} {H_0E (z) ^ {\ frac {1} {2}} (1 + z)} $$

Wenn wir das Alter des Universums bei einer bestimmten Rotverschiebung finden wollen ‘z’ dann -

$$ t (z) = \ frac {1} {H_0} \ int _ {\ infty} ^ {z_1} \ frac {-1} {E (z) ^ {\ frac {1} {2}} (1+) z)} dz $$

Wo k ist der Krümmungsdichteparameter und -

$$ E (z) \ äquiv \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega_ {rad, 0} (1 + z) ^ 4 + \ Omega_ {k, 0} (1 + z) ^ 2 + \ Omega _ {\ wedge, 0} $$

Um das gegenwärtige Alter des Universums zu berechnen, nehmen Sie z₁ = 0.

$$ t (z = 0) = t_ {Alter} = t_0 = \ frac {1} {H_0} \ int _ {\ infty} ^ {z_1} \ frac {-1} {E (z) ^ {\ frac { 1} {2}} (1 + z)} dz $$

Für das Einstein-Desitter-Modell, dh $ \ Omega_m = 1 $, $ \ Omega_ {rad} = 0 $, $ \ Omega_k = 0 $, $ \ Omega_ \ wedge = 0 $, wird die Gleichung für das Alter des Universums - -

$$ t_ {age} = \ frac {1} {H_0} \ int_ {0} ^ {\ infty} \ frac {1} {(1 + z) ^ {\ frac {5} {2}}} dz $ $

Nach dem Lösen des Integrals erhalten wir -

$$ t_H = \ frac {2} {3H_0} $$

Der Nachthimmel ist wie ein Cosmic Time Machine.Wann immer wir einen fernen Planeten, Stern oder eine Galaxie beobachten, sehen wir ihn so, wie er vor Stunden, Jahrhunderten oder sogar Jahrtausenden war. Dies liegt daran, dass sich Licht mit einer endlichen Geschwindigkeit (der Lichtgeschwindigkeit) fortbewegt und angesichts der großen Entfernungen im Universum Objekte nicht so sehen, wie sie jetzt sind, sondern so, wie sie waren, als das Licht emittiert wurde. Die Zeit, die zwischen dem Zeitpunkt, an dem wir das Licht hier auf der Erde erfassen, und dem Zeitpunkt, an dem es ursprünglich von der Quelle emittiert wurde, verstrichen ist, wird als bezeichnetLookback Time (t_L(z₁)).

Die Lookback-Zeit ist also gegeben durch -

$$ t_1 (z_1) = t_0-t (z_1) $$

Die Lookback-Zeit für das Einstein Desitter Universe ist -

$$ t_L (z) = \ frac {2} {3H_0} \ left [1- \ frac {1} {(1 + z) ^ {\ frac {3} {2}}} \ right] $$

Punkte, die man sich merken sollte

• Wann immer wir einen fernen Planeten, Stern oder eine Galaxie beobachten, sehen wir ihn so, wie er vor Stunden, Jahrhunderten oder sogar Jahrtausenden war.

• Die Zeit zwischen dem Zeitpunkt, an dem wir das Licht hier auf der Erde erfassen und dem Zeitpunkt, an dem es ursprünglich von der Quelle emittiert wurde, wird als Lookback-Zeit bezeichnet.

In diesem Kapitel werden wir verstehen, was der Winkeldurchmesserabstand ist und wie er in der Kosmologie hilft.

Für das gegenwärtige Universum -

• $ \ Omega_ {m, 0} \: = \: 0,3 $

• $ \ Omega _ {\ wedge, 0} \: = \: 0.69 $

• $ \ Omega_ {rad, 0} \: = \: 0.01 $

• $ \ Omega_ {k, 0} \: = \: 0 $

Wir haben bisher zwei Arten von Entfernungen untersucht -

• Proper distance (lp) - Die Entfernung, die Photonen von der Quelle zu uns zurücklegen, dh die Instantaneous distance.

• Comoving distance (lc) - Abstand zwischen Objekten in einem Raum, der sich nicht ausdehnt, dh distance in a comoving frame of reference.

Entfernung als Funktion der Rotverschiebung

Stellen Sie sich eine Galaxie vor, die gleichzeitig ein Photon ausstrahlt t₁ welches vom Beobachter bei erkannt wird t₀. Wir können den richtigen Abstand zur Galaxie schreiben als -

$$ l_p = \ int_ {t_1} ^ {t_0} cdt $$

Lass die Rotverschiebung der Galaxie sein z,

$$ \ Rightarrow \ frac {\ mathrm {d} z} {\ mathrm {d} t} = - \ frac {1} {a ^ 2} \ frac {\ mathrm {d} a} {\ mathrm {d} t} $$

$$ \ Rightarrow \ frac {\ mathrm {d} z} {\ mathrm {d} t} = - \ frac {\ frac {\ mathrm {d} a} {\ mathrm {d} t}} {a} \ frac {1} {a} $$

$$ \ also \ frac {\ mathrm {d} z} {\ mathrm {d} t} = - \ frac {H (z)} {a} $$

Jetzt jederzeit die Entfernung der Galaxie t wird sein -

$$ l_c = \ frac {l_p} {a (t)} $$

$$ l_c = \ int_ {t_1} ^ {t_0} \ frac {cdt} {a (t)} $$

In Bezug auf z,

$$ l_c = \ int_ {t_0} ^ {t_1} \ frac {cdz} {H (z)} $$

Es gibt zwei Möglichkeiten, Entfernungen zu finden:

Fluss-Leuchtkraft-Beziehung

$$ F = \ frac {L} {4 \ pi d ^ 2} $$

wo d ist die Entfernung an der Quelle.

Der Winkeldurchmesserabstand einer Quelle

Wenn wir die Größe einer Quelle kennen, sagt uns ihre Winkelbreite den Abstand zum Beobachter.

$$ \ theta = \ frac {D} {l} $$

wo l ist der Winkeldurchmesserabstand der Quelle.

• θ ist die Winkelgröße der Quelle.

• D ist die Größe der Quelle.

Betrachten Sie eine Galaxie der Größe D und der Winkelgröße dθ.

Wir wissen das,

$$ d \ theta = \ frac {D} {d_A} $$

$$ \ also D ^ 2 = a (t) ^ 2 (r ^ 2 d \ theta ^ 2) \ quad \ weil dr ^ 2 = 0; \: d \ phi ^ 2 \ ca. 0 $$

$$ \ Rightarrow D = a (t) rd \ theta $$

Ändern r zu r_c, die kommende Entfernung der Galaxie, haben wir -

$$ d \ theta = \ frac {D} {r_ca (t)} $$

Hier, wenn wir wollen t = t₀Am Ende messen wir die gegenwärtige Entfernung zur Galaxie. AberDwird zum Zeitpunkt der Emission des Photons gemessen. Daher mitt = t₀erhalten wir eine größere Entfernung zur Galaxie und damit eine Unterschätzung ihrer Größe. Deshalb sollten wir die Zeit nutzent₁.

$$ \ also d \ theta = \ frac {D} {r_ca (t_1)} $$

Wenn wir dies mit dem vorherigen Ergebnis vergleichen, erhalten wir -

$$ d_ \ wedge = a (t_1) r_c $$

$$ r_c = l_c = \ frac {d_ \ wedge} {a (t_1)} = d_ \ wedge (1 + z_1) \ quad \ weil 1 + z_1 = \ frac {1} {a (t_1)} $$

Deshalb,

$$ d_ \ wedge = \ frac {c} {1 + z_1} \ int_ {0} ^ {z_1} \ frac {dz} {H (z)} $$

d_A ist der Winkeldurchmesserabstand für das Objekt.

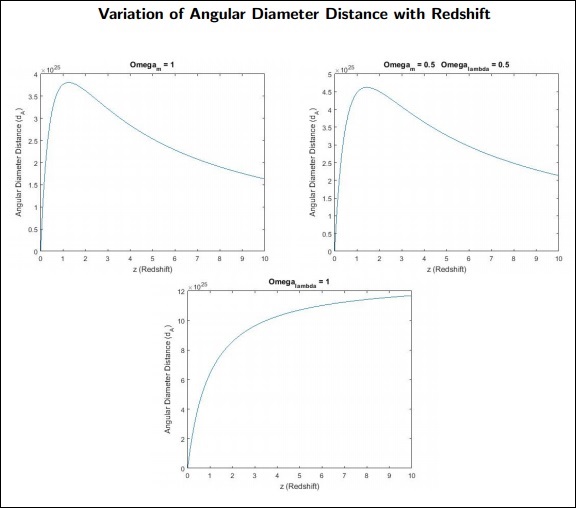
Punkte, die man sich merken sollte

• Wenn wir die Größe einer Quelle kennen, sagt uns ihre Winkelbreite den Abstand zum Beobachter.

• Die richtige Entfernung ist die Entfernung, die Photonen von der Quelle zu uns zurücklegen.

• Die Entfernung ist die Entfernung zwischen Objekten in einem Raum, der sich nicht ausdehnt.

Wie im vorherigen Kapitel erläutert, verschiebt sich der Winkeldurchmesser zu einer Quelle bei Rotverschiebung z ist gegeben durch -

$$ d_ \ wedge (z_ {gal}) = \ frac {c} {1 + z_ {gal}} \ int_ {0} ^ {z_ {gal}} \ frac {1} {H (z)} dz $ $

$$ d_ \ wedge (z_ {gal}) = \ frac {r_c} {1 + z_ {gal}} $$

Dabei ist $ r_c $ die Entfernung.

Die Leuchtkraftentfernung hängt von der Kosmologie ab und ist definiert als die Entfernung, in der der beobachtete Fluss auftritt f ist von einem Objekt.

Wenn die intrinsische Leuchtkraft $ d_L $ eines entfernten Objekts bekannt ist, können wir seine Leuchtkraft berechnen, indem wir den Fluss $ f $ messen, der bestimmt wird durch -

$$ d_L (z) = \ sqrt {\ frac {L} {4 \ pi f}} $$

Die Photonenenergie wird rot verschoben.

$$ \ frac {\ lambda_ {obs}} {\ lambda_ {emi}} = \ frac {a_0} {a_e} $$

wobei $ \ lambda_ {obs}, \ lambda_ {emi} $ beobachtet und emittierte Wellenlängen und $ a_0, a_e $ entsprechende Skalierungsfaktoren sind.

$$ \ frac {\ Delta t_ {obs}} {\ Delta t_ {emi}} = \ frac {a_0} {a_e} $$

Dabei wird $ \ Delta_t {obs} $ als Photonenzeitintervall beobachtet, während $ \ Delta_t {emi} $ das Zeitintervall ist, in dem sie emittiert werden.

$$ L_ {emi} = \ frac {nhv_ {emi}} {\ Delta t_ {emi}} $$

$$ L_ {obs} = \ frac {nhv_ {obs}} {\ Delta t_ {obs}} $$

$ \ Delta t_ {obs} $ benötigt mehr Zeit als $ \ Delta t_ {emi} $, da der Detektor alle Photonen empfangen sollte.

$$ L_ {obs} = L_ {emi} \ left (\ frac {a_0} {a_e} \ right) ^ 2 $$

$$ L_ {obs} <L_ {emi} $$

$$ f_ {obs} = \ frac {L_ {obs}} {4 \ pi d_L ^ 2} $$

Für ein nicht expandierendes Universum entspricht die Leuchtdistanz der kommenden Entfernung.

$$ d_L = r_c $$

$$ \ Rightarrow f_ {obs} = \ frac {L_ {obs}} {4 \ pi r_c ^ 2} $$

$$ f_ {obs} = \ frac {L_ {emi}} {4 \ pi r_c ^ 2} \ left (\ frac {a_e} {a_0} \ right) ^ 2 $$

$$ \ Rightarrow d_L = r_c \ left (\ frac {a_0} {a_e} \ right) $$

Wir finden den Helligkeitsabstand $ d_L $ zur Berechnung der Helligkeit des emittierenden Objekts $ L_ {emi} $ -

• Interpretation - Wenn wir die Rotverschiebung kennen zVon jeder Galaxie können wir $ d_A $ herausfinden und daraus $ r_c $ berechnen. Dies wird verwendet, um $ d_L $ herauszufinden.

• Wenn $ d_L! = r_c (a_0 / a_e) $, dann können wir Lemi nicht aus $ f_ {obs} $ finden.

Die Beziehung zwischen dem Helligkeitsabstand $ d_L $ und dem Winkeldurchmesserabstand $ d_A. $

Wir wissen das -

$$ d_A (z_ {gal}) = \ frac {d_L} {1 + z_ {gal}} \ left (\ frac {a_0} {a_e} \ right) $$

$$ d_L = (1 + z_ {gal}) d_A (z_ {gal}) \ left (\ frac {a_0} {a_e} \ right) $$

Der Skalierungsfaktor bei der Emission von Photonen ist gegeben durch -

$$ a_e = \ frac {1} {(1 + z_ {gal})} $$

Der Skalierungsfaktor für das gegenwärtige Universum ist -

$$ a_0 = 1 $$

$$ d_L = (1 + z_ {gal}) ^ 2d_ \ wedge (z_ {gal}) $$

Welches soll man entweder $ d_L $ oder $ d_A $ wählen?

• Für eine Galaxie bekannter Größe und Rotverschiebung zur Berechnung ihrer Größe wird $ d_A $ verwendet.

• Wenn es eine Galaxie einer bestimmten scheinbaren Größe gibt, wird $ d_L $ verwendet, um herauszufinden, wie groß sie ist.

Example - Wenn gegeben ist, dass zwei Galaxien gleicher Rotverschiebung (z = 1) und in der Ebene des Himmels durch getrennt sind 2.3 arc sec Was ist dann die maximale physische Trennung zwischen diesen beiden?

Verwenden Sie dazu $ d_A $ wie folgt:

$$ d_A (z_ {gal}) = \ frac {c} {1 + z_ {gal}} \ int_ {0} ^ {z_ {gal}} \ frac {1} {H (z)} dz $$

wobei z = 1 H (z) basierend auf den kosmologischen Parametern der Galaxien ersetzt.

Punkte, die man sich merken sollte

• Der Helligkeitsabstand hängt ab von cosmology.

• Wenn die intrinsische Leuchtkraft $ d_L $ eines entfernten Objekts bekannt ist, können wir seine Leuchtkraft durch Messen des Flusses berechnen f.

• Für ein nicht expandierendes Universum entspricht der Helligkeitsabstand dem comoving distance.

• Der Helligkeitsabstand ist immer größer als der Angular Diameter Distance.

Für jede gegebene Rotverschiebung (z) haben wir zwei Werte für die Entfernung -

• Winkeldurchmesserabstand (d _A )
• Leuchtkraftabstand (d _L )

Es gibt keine eindeutige Definition der „kosmologischen“ Distanz im Universum. Die Wahl des Abstands hängt vom Zweck und der Zweckmäßigkeit der Anwendung ab.

Um den vorhergesagten Trend zu testen, wie sich die Winkelgröße eines Objekts mit der Rotverschiebung ändert, wird ein Maßstab in Standardgröße am Himmel benötigt. Dies sollte ein Objekt sein, das -

• ist sehr leuchtend, so dass es bei z> 1 erkannt werden kann.

• ist sehr groß, so dass wir seine Winkelgröße auflösen können.

• hat sich über die kosmologisch signifikante Zeit nicht morphologisch entwickelt (z ∼ 1 entspricht einer Rückblickzeit von etwa 7 Gyr).

Einige Objekte (wie cD-Galaxien) erfüllen die ersten beiden Kriterien. Es wurde jedoch festgestellt, dass sich fast jedes Objekt mit der Zeit morphologisch entwickelt. Im Allgemeinen sind astrophysikalische Objekte (erweiterte Quellen) in der Vergangenheit von Natur aus kleiner, da sie sich noch bilden.

Leuchtkraftabstand

Die Leuchtdistanz hängt von der Kosmologie ab. Die Abhängigkeit des Leuchtkraftabstands von der Kosmologie macht es zu einem nützlichen Maß für die kosmologischen Parameter.

Die kosmologischen Parameter können geschätzt werden, wenn wir eine Standardkerze finden, die sich nicht intrinsisch entwickelt und vom lokalen zum Universum mit hoher Rotverschiebung existiert.

Eine Standardkerze unterscheidet sich in ihrer Leuchtkraft nicht von Quelle zu Quelle. Die Voraussetzung ist, dass jeder Unterschied in der geschätzten Leuchtkraft von Standardkerzen kosmologisch bedingt sein muss. Eine solche Kerze ist Typ Ia Supernovae.

Typ 1a Supernovae (SNe)

Dies ist das Ergebnis der Explosion eines weißen Zwergs nach ausreichender Massenakkretion durch seinen Begleiter, einen roten Riesen oder einen ähnlichen Hauptreihenstern, in einem binären System. Nachdem der rote Riese näher als der Roche-Lappenabstand des Weißen Zwergs gekommen ist, beginnt der Stofftransfer und schließlich explodiert der Weiße Zwerg und gibt eine große Menge Energie ab, wobei kein Kern zurückbleibt. Diese werden als Typ 1a Supernovae bezeichnet. Die typische Explosionsrate von Supernovae vom Typ 1a in einer Galaxie beträgt 1 pro Jahrhundert.

Die Suche nach SNe vom Typ 1a wurde mit verschiedenen Teams durchgeführt -

• High z Supernova-Suchteam (Brian Schmidt, Adam Reiss et al.)
• Supernova Cosmology Project (Saul Perlmutter et al.)

Es gab ein anderes Forschungsteam namens Carnegie Supernovae Project wer hat ähnliche Ergebnisse gegeben.

Die Ähnlichkeit der Ergebnisse verschiedener Teams zeigt die kosmologische Natur von Typ 1a SNe. Daher sind sie effiziente Standardkerzen.

Punkte, die man sich merken sollte

• Es gibt keine eindeutige Definition der „kosmologischen“ Distanz im Universum.

• Winkeldurchmesserabstand und Leuchtkraftabstand werden am häufigsten verwendet.

• Eine Standardkerze ist eine Kerze, die sich in ihrer Leuchtkraft von Quelle zu Quelle nicht unterscheidet.

• Typ 1a SNe erfüllt die Kriterien einer Standardkerze.

Das CMB (Cosmic Microwave Background) besteht im Wesentlichen aus den Photonen der Zeit, als sich Materie und Strahlung im Gleichgewicht befanden. In den 1920er Jahren wurde die Idee eines expandierenden Universums akzeptiert und konnte mehrere Fragen beantworten. Fragen zur Fülle schwererer Elemente und zur Fülle blieben jedoch unbeantwortet. Darüber hinaus implizierte das expandierende Universum, dass die Dichte der Materie auf 0 sinken sollte.

1948 erklärten George Gammow und Ralph Alpher mit „Big Bang“ den Ursprung schwererer Elemente und die Fülle. Zusammen mit Robert Herman sagten sie die Existenz von "Reliktstrahlung" oder Strahlung aus dem "Urknall" voraus. Die vorhergesagte Temperatur für diese Reststrahlung lag zwischen 50 und 6 K. 1965 entdeckten Robert Dicke, Jim Peebles und David Wilkinson zusammen mit der Forschungsgruppe von Amo Perizias experimentell den CMB.

Das frühe Universum war sehr heiß und die Energie war zu hoch, als dass die Materie neutral bleiben könnte. Daher lag die Materie in ionisierter Form vor -Plasma. Die Strahlung (Photonen) und Materie (Plasma) wechselwirkten hauptsächlich durch die folgenden drei Prozesse.

• Compton Scattering - (Hauptwechselwirkungsprozess) Inelastische Streuung zwischen hochenergetischen Photonen und energiearmen geladenen Teilchen.

• Thomson Scattering - Elastische Streuung von Photonen durch ein frei geladenes Teilchen.

• Inverse Compton Scattering- Hochenergetische geladene Teilchen und energiearme Photonen. Diese Wechselwirkungen führten schließlich dazu, dass sich Materie und Strahlung im thermischen Gleichgewicht befanden.

Thermisches Gleichgewicht

Im thermischen Gleichgewicht gehorcht die Strahlung dem Planck Distribution of Energy,

$$ B_v (T) = \ frac {2hv ^ 3} {c (e ^ {hv / k_BT} -1)} $$

Während dieser Zeit war der mittlere freie Weg der Photonen aufgrund der sehr häufigen Wechselwirkungen sehr klein. Das Universum war strahlungsundurchlässig. Das frühe Universum war strahlungsdominiert. Das Universum entwickelte sich so, dass Materie und Strahlung das thermische Gleichgewicht erreichten und ihre Energiedichte gleich wurde. Dies ist aus dem Diagramm ersichtlich, das die Entwicklung der Dichte mit dem Skalierungsfaktor zeigt. Lassen Sie uns den Skalierungsfaktor (Zeit) (a (t)) herausfinden, bei dem die Materie und die Strahlung das Gleichgewicht erreicht haben.

$$ \ rho_m \ propto \ frac {1} {a ^ 3}, \: \ rho_r \ propto \ frac {1} {a ^ 4} $$

$$ \ frac {\ rho_ {m, t}} {\ rho_ {r, t}} = \ frac {\ Omega_ {m, t}} {\ Omega_ {r, t}} = \ frac {\ Omega_ { m, 0}} {\ Omega_ {r, 0}} a (t) $$

Im Gleichgewicht

$$ \ frac {\ rho_ {m, t}} {\ rho_ {r, t}} = \ frac {\ Omega_ {m, t}} {\ Omega_ {r, t}} = 1 $$

$$ \ Rightarrow \ frac {\ Omega_ {m, 0}} {\ Omega_ {r, 0}} a (t) = 1 \: \ Rightarrow a (t) = 2,96 \ mal 10 ^ {- 4} $$

Verwenden von $ \ Omega_ {m, 0} = 0,27 $ und $ \ Omega_ {r, 0} = 8 \ mal 10 ^ {- 5} $. Die diesem Skalierungsfaktor entsprechende Rotverschiebung ist gegeben durch -

$$ z = 1 / a (t) -1 \ ca. 3375 $$

Die Energiedichte der Strahlung nahm aufgrund der Expansion des Universums ab. So begann sich das Universum abzukühlen. Als die Energie der Photonen abnahm, begannen sich neutrale Atome zu bilden. Um eine Rotverschiebung von 1300 begann sich neutraler Wasserstoff zu bilden. Diese Ära hatte eine Temperatur nahe 3000K.

Die Wechselwirkung zwischen Materie und Strahlung wurde sehr selten und so wurde das Universum für Strahlung transparent. Dieser Zeitraum wird aufgerufen“Surface of last scattering”da der mittlere freie Weg der Photonen sehr groß wurde, wodurch nach dieser Zeit kaum eine Streuung stattfand. Es wird auch als bezeichnet“Cosmic Photosphere”.

Punkte, die man sich merken sollte

• CMB besteht aus den Photonen der Zeit, als Materie und Strahlung im Gleichgewicht waren.

• Das frühe Universum war sehr heiß und die Energie war zu hoch, als dass die Materie neutral bleiben könnte. Sie existierte also als Plasma mit ionisierter Materie.

• Compton Scattering, Thomson Scattering und Inverse Compton Scattering waren damals die drei Wechselwirkungsprozesse zwischen Materie und Strahlung.

• Das Universum entwickelte sich so, dass Materie und Strahlung das thermische Gleichgewicht erreichten.

Wir sollten zuerst verstehen, was das auszeichnet decoupling. Wir wissen, dass die Energien so viel höher waren, dass Materie nur in Form von existierteIonized Particles. Bei Entkopplungs- und Rekombinationsepochen musste die Energie daher abfallen, um die Ionisierung von Wasserstoff zu ermöglichen. Zur Schätzung der Temperatur zum Zeitpunkt der Entkopplung kann eine ungefähre Berechnung vorgenommen werden.

Dies wurde wie folgt durchgeführt:

Betrachten Sie zunächst nur die Ionisierung von Wasserstoff im Grundzustand.

$$ hv \ approx k_BT $$

$$ \ also T \ approx \ frac {hv} {k_B} $$

Zur Ionisierung des Grundzustands Wasserstoff, hν ist 13,6 eV und kB ist der Boltzmann Constant8,61 × 10 ^–5 eV / K, was zeigt, dass die Temperatur 1,5 × 105 Kelvin beträgt.

Dies sagt uns im Wesentlichen, dass sich die neutralen Atome bilden können , wenn die Temperatur unter 1,5 × 10 ⁵ K liegt.

Wir wissen, dass das Verhältnis von Photonen zu Baryonen etwa 5 × 10 ¹⁰ beträgt . Selbst am Ende des Graphen, wo sich die Anzahl der Photonen verringert, gibt es immer noch genügend Photonen, um die Wasserstoffatome zu ionisieren. Darüber hinaus garantiert die Rekombination von Elektron und Proton kein Wasserstoffatom im Grundzustand. Anregungszustände erfordern weniger Energie für die Ionisation. Daher sollte von Fall zu Fall eine disziplinierte statistische Analyse durchgeführt werden, um einen genauen Wert zu erhalten. Berechnungen haben die Temperatur auf etwa 3000 K festgelegt.

Zur Erklärung betrachten wir den Fall der Anregung von Wasserstoff in den ersten angeregten Zustand. Der allgemeine Ausdruck für das Verhältnis der Anzahl der Photonen mit einer Energie von mehr alsΔE, Nγ (> ΔE) auf die Gesamtzahl der Photonen Nγ ist gegeben durch -

$$ \ frac {N_ \ gamma (> \ Delta E)} {N_ \ gamma} \ propto e ^ {\ frac {- \ Delta E} {kT}} $$

Für den Fall der Anregung von Wasserstoff in den ersten angeregten Zustand ΔEbeträgt 10,2 eV. Wenn wir nun eine sehr konservative Zahl von mindestens 1 Photon mit einer Energie von mehr als 10,2 für jedes Baryon betrachten (unter Berücksichtigung des Verhältnisses von 5 × 10 ¹⁰ erhalten wir die Temperatur aus der Gleichung 3 als 4800 K (eingefügtes Nγ (>) ΔE) = Np).

Dies ist die Temperatur, um im ersten angeregten Zustand eine Population neutraler Wasserstoffatome zu erzeugen. Die Temperatur, um dies zu ionisieren, ist signifikant niedriger. Somit erhalten wir eine bessere Schätzung als 1,5 × 10 ⁵ K, die näher am akzeptierten Wert von 3000 K liegt.

Rotverschiebung - Temperaturbeziehung

Um die Beziehung zwischen Rotverschiebung und Temperatur zu verstehen, wenden wir die folgenden zwei Methoden an, wie unten beschrieben.

Methode 1

Von Wien’s Law, Wir wissen das

$$ \ lambda_mT = Konstante $$

Um dies mit der Rotverschiebung in Beziehung zu setzen, verwenden wir -

$$ 1 + z = \ frac {\ lambda_0} {\ lambda_e} $$

Als $ λ_oT_o = λ_eT (z) $ erhalten wir -

$$ T (z) = T_0 \ frac {\ lambda_0} {\ lambda_e} = T_0 (1 + z) $$

Rahmen T_o Als aktueller Wert 3K können wir Temperaturwerte für eine gegebene Rotverschiebung erhalten.

Methode 2

In Bezug auf die Häufigkeit wissen wir -

$$ v_0 = \ frac {v_e} {1 + z} $$

$$ B_vdv = \ frac {2hv ^ 3} {c ^ 2} \ frac {dv} {e ^ {hv / kT} -1} $$

Dies sagt uns über die Nettoenergie der Photonen für ein Energieintervall und hνist die Energie eines einzelnen Photons. Daher können wir die Anzahl der Photonen durch erhaltenBνdν/hν.

Wenn $ n_ {νo} $ für Gegenwart und $ n_ {νe} $ für emittiert ist, erhalten wir -

$$ \ frac {n_ {v_e}} {n_ {v_0}} = (1 + z) ^ 3 $$

Bei Vereinfachung erhalten wir,

$$ n_ {v_0} = \ frac {2v_c ^ 2} {c ^ 2} \ frac {dv_c} {e ^ {hv / kT} -1} \ frac {1} {(1 + z) ^ 3} = \ frac {2v_0 ^ 2} {c ^ 2} \ frac {dv_c} {e ^ {hv / kT} -1} $$

Das gibt uns die Wien’s Law wieder und somit kann geschlossen werden, dass -

$$ T (z) = T_0 \ frac {\ lambda_0} {\ lambda_e} = T_0 (1 + z) $$

Punkte, die man sich merken sollte

• Das frühe Universum war sehr heiß, 3000K.
• Aktuelle Messungen zeigen, dass die Temperatur des Universums nahe bei 3 K liegt.
• Je weiter wir in der Zeit zurückliegen, desto proportionaler steigt die Temperatur.

In diesem Kapitel werden wir die Anisotropie von CMB-Strahlung und COBE, dh Cosmic Background Explorer, diskutieren.

Primäre Anisotropien im CMB

Um die Beobachtungen aus dem Weltraum und die primären Anisotropien in der kosmischen Mikrowellen-Hintergrundstrahlung zu verstehen, nehmen wir die folgenden Gleichungen und verstehen sie wie unten gezeigt.

CMB-Photonenzahldichte (n _γ , 0)

$$ n _ {\ gamma, 0} = \ frac {Gesamt \: Energie \: Dichte} {Charakteristik \: Energie \: von \: Photonen} $$

$$ n _ {\ gamma, 0} = \ frac {aT_0 ^ 4} {k_BT_0} $$

Wo $ k_B $ ist Boltzmann Constant und $ T_0 $ ist das present temperature of the universe.

Unter Verwendung der gegenwärtigen Temperatur $ (T_0) $ als 2,7 K erhalten wir die aktuelle CMB-Photonenzahldichte als 400 cm ^–3 .

Die Dichte der kosmischen Sternphotonenzahl ist über große Maßstäbe viel kleiner (∼ = 10 ^–3 cm ^–3 ).

Verhältnis von Baryon zu Photon (η)

Wenn die Sternbeiträge von Galaxien, die sich mit CMB vermischen, vernachlässigbar sind, beträgt das Verhältnis von Baryon zu Proton -

$$ \ eta = \ frac {n_ {b, 0}} {n _ {\ gamma, 0}} $$

Der aktuelle Wert beträgt ~ 5 × 10 ^–10 . Da sowohl die Photonen- als auch die Baryonenzahldichte proportional zu sinda⁻³, dann η entwickelt sich nicht mit der Zeit.

Energiedichte

Im Gegensatz zur Zahlendichte ist die Materieenergiedichte derzeit stärker dominiert als die Photonenenergiedichte.

Die Energiedichte der baryonischen Materie = $ \ rho_ {b, 0} c ^ 2 = 0,04 \ rho_cc ^ 2 = 2 × 10 ^ {- 9} ergcm ^ {- 3} $. Während die Energiedichte der Strahlung = $ aT_0 ^ 4 = 4 \ mal 10 ^ {- 13} ergcm {−3} $.

Isotropie der CMB-Strahlung

Penzias und Wilsonfanden heraus, dass der CMB innerhalb der Grenzen der Beobachtungen isotrop ist. Die Grenzen sind niedrige Winkelauflösung und Empfindlichkeit der Instrumente. Sie machten Beobachtungen von der Erde aus, daher können Beobachtungen nicht über das gesamte Spektrum gemacht werden, da Wasserdampf in der Atmosphäre viele Wellenlängen im Bereich von 1 mm bis 1 m absorbiert. CMB kann also nicht als Spektrum behauptet werden.

Es wird angenommen, dass der CMB rotationsinvariant (isotrop) ist. Da es eine Zeit gab, in der Materie und Strahlung im Gleichgewicht waren, ist die Bildung von Strukturen im Universum unerklärlich. Da die Verteilung der Materie nicht isotrop ist, sondern wie ein kosmisches Netz mit großen Hohlräumen dazwischen zusammengeklumpt ist, wird angenommen, dass CMB einen extragalaktischen Ursprung hat.

Zu Beginn der Beobachtungen aus dem Weltraum wurden jedoch Anisotropien im CMB gefunden, die zu der Annahme führten, dass diese Anisotropien in der Materie zur Bildung von Strukturen führen.

Beobachtung der CMB-Strahlung aus dem Weltraum

Die Hauptsatelliten, die zur Beobachtung des CMB gestartet wurden, waren -

• Cosmic Microwave Background Explorer (COBE, 1989)

• Wilkinson Microwave Anisotropy Probe (WMAP, 2001) und

• Planck (2009).

COBE (Cosmic Background Explorer)

COBE hatte hauptsächlich zwei Instrumente. Sie sindFar InfraRed Absolute Spectrometer (FIRAS) und Differential Microwave Radiometers(DMR-Antennen). FIRAS misst die Intensität des CMB als Funktion der Wellenlänge entlang einer bestimmten Richtung. Während DMR 3 Antennen hat, um den Intensitätsunterschied von CMB aus drei verschiedenen Richtungen zu messen. Die folgenden Hinweise geben uns weitere Informationen zu FIRAS und DMR.

• CMB-Beobachtungen von FIRAS zeigen, dass die CMB-Strahlung dem Schwarzkörperspektrum bei T = 2,72528 ± 0,00065 K entspricht.

• Das DMR misst drei Frequenzen (31,5 GHz, 53 GHz, 90 GHz) in alle Himmelsrichtungen.

• Das „rote Batman-Symbol“ in den DMR-Beobachtungen ist Rauschen aus der Vordergrundemission (galaktische diffuse Synchrotronemission).

• Die Intensitätsschwankungen in den Beobachtungen entsprechen Temperaturschwankungen. Das Vorhandensein von heißen und kalten Stellen beweist, dass die CMB-Strahlung anisotrop ist.

• Diese Anisotropie muss zum Zeitpunkt der Entkopplung vorliegen, da es keine Verzerrungen in CMB gibt. Materie sollte also einige Taschen mit einer höheren Dichte als die anderen haben.

COBE-Ergebnisse

Das CMB-Spektrum (Intensität als Funktion der Energie) ist nahezu ein perfekter schwarzer Körper, der T = 2,7 K entspricht. Die spezifische Intensität der CMB-Strahlung ist für alle Richtungen nahezu gleich. Bestätigung, dass das Universum im großen Maßstab isotrop ist (bestätigt unsere Annahme des kosmologischen Prinzips).

Die Analyse der Daten zeigte, dass es bei der Auflösung von COBE (DMR) Temperaturanisotropien („Schwankungen“) im CMB-Spektrum gibt.

Resolution of COBE, WMAP, Planck

• Das an Bord befindliche DMR-Instrument COBE hatte eine begrenzte (maximale) räumliche Auflösung von ∼ 7 Grad.

• Die Wilkinson-Mikrowellenanisotropiesonde (WMAP) hatte eine durchschnittliche Auflösung von ≤ 0,7 Grad.

• Der Planck-Satellit hat eine Winkelauflösung von ∼ 10 Bogenminuten.

Punkte, die man sich merken sollte

• Die Dichte der kosmischen Sternphotonenzahl ist viel kleiner als die CMB-Photonenzahldichte.

• Wir leben in einem von Materie dominierten Universum, da die Energiedichte der Materie höher ist als die Photonenenergiedichte.

• COBE, WMAP, Planck sind Bemühungen, Anisotropien in der CMB zu messen und zu quantifizieren.

• Die Strukturbildung im Universum ist ein Ergebnis von CMB-Anisotropien.

Wenn wir uns die verfeinerte, korrigierte CMB-Karte für den gesamten Himmel ansehen, gibt es eine Menge Vordergrundkontamination, was eine Art ist anisotropyin diesen Karten. Wir können sehen, dass diese Vordergrundemissionen aus der Milchstraßengalaxie stammen. Die Intensität von CMB ist entlang der Ebene der galaktischen Ebene hoch und nimmt mit zunehmender Intensität ab. In diesen können wir sekundäre Anisotropien beobachten, bei denen es sich um Synchrotronemissionen aus der Galaxie handelt. Diese Emissionen bilden die Vordergrundkontamination. Um die CMB-Emission vom Himmel zu betrachten, müssen wir diese Vordergrundemissionen subtrahieren.

Das folgende Bild zeigt den CMB mit Vordergrundemissionen.

Dipolanisotropie

Es gibt eine andere Art von Anisotropie, die in der CMB-All-Sky-Karte gefunden wurde und als Dipol-Anisotropie bezeichnet wird. Es ist nicht mit dem frühen Universum verbunden. Dies kann mit sphärischen harmonischen Funktionen dargestellt werden. Wenn sich auf der sphärischen Oberfläche ein Muster befindet und wir es mit mathematischen Funktionen abbilden möchten, können wir dies mit trigonometrischen Funktionen tun. Wenn wir also abbilden, kann es sich um einen Monopol handeln, der in jeder Richtung gleich ist, oder um einen Dipol, der die Eigenschaften umdreht, wenn er um 180 Grad gedreht wird. Ebenso haben wir Quadrupol und so weiter. Für ein komplexes Muster kann es als die Summe dieser Monopole, Dipole, Quadrupole usw. ausgedrückt werden.

Das CMB wird so modelliert, dass eine der Hauptquellen der Anisotropie in der All-Sky-Karte diese Dipolanisotropie ist, aber es ist keine ursprüngliche Modellierung des CMB. Dies ist im Bild unten zu sehen.

Die Dipolrichtung, die wir sehen, ist keine zufällige Richtung. Die Dipolanisotropie hat eine Richtung. Wir sehen die CMB-Intensität entlang einer bestimmten Richtung. Diese Richtung ist auf den Geschwindigkeitsvektor des Sonnensystems zurückzuführen. Die Geschwindigkeit der Erde kann in Bezug auf die Sonne oder den Mittelpunkt der Galaxie dargestellt werden. In der Richtung, in die sich die Erde bewegt, beobachten wir eine Blueshift und eine Rotverschiebung, und der Dipol liegt in dieser Richtung.

Das obige Bild hat ein typisches Dipol-Erscheinungsbild, da sich unsere Galaxie in eine bestimmte Richtung bewegt. Das Ergebnis ist - eine Seite des Himmels erscheint rotverschoben und die andere Seite des Himmels erscheint blauverschoben. In diesem Fall bedeutet Rotverschiebung, dass die Photonen eine längere Wellenlänge haben = kühler (also sehen sie im obigen Diagramm rückwärts von ihrem Namen blau aus).

Wir können sagen, dass sich die Erde zu einem bestimmten Zeitpunkt in einer bestimmten Richtung in Bezug auf Sonne / galaktisches Zentrum / CMB am Himmel bewegt. Wenn wir dann einen beliebigen Winkel betrachten und die Temperatur für CMB messen, wäre dies anders. Dies liegt daran, dass wir Photonen messen, die entweder blauverschoben oder rotverschoben sind und von der Sichtlinie der Photonen am Himmel abhängen.

Punkte, die man sich merken sollte

• Die Vordergrundkontamination in CMB All Sky Map wird als Anisotropie von CMB bezeichnet.

• Diese Emissionen stammen aus unserer eigenen Milchstraßengalaxie.

• Die 2 Arten von Anisotropien sind: Dipolanisotropie und Winkelleistungsspektrumanisotropie.

• Die Dipolanisotropie verläuft in einer bestimmten Richtung, während die Anisotropie des Winkelleistungsspektrums überall verteilt ist.

Die Horizontlänge ist die Entfernung, die Lichtphotonen von 'The Big Bang' bis 'The Recombination Era' zurücklegen. Die 1 ^st Peak des Winkelspektrums ist bei θ = 1◦ (L = 180), die eine sehr spezielle Längenskala ist.

Der richtige Abstand zwischen zwei Punkten ist gegeben durch -

$$ r_p = \ int_ {0} ^ {t} cdt $$

Wenn wir den Zeitrahmen von t = 0 bis t = t _{rec nehmen} , dann

$$ r_H = \ int_ {0} ^ {t_ {rec}} cdt $$

Wobei $ r_H $ die richtige Horizontentfernung ist.

Jetzt wissen wir, dass -

$$ \ dot {a} = \ frac {\ mathrm {d} a} {\ mathrm {d} t} $$

$$ dt = \ frac {da} {\ dot {a}} $$

Wenn t = 0 ist, ist a = 0.

Dann ist $ t = t_ {rec}, a = a_0 / (1 + z_ {rec}) $.

Daher können wir schreiben,

$$ r_H (z_ {rec}) = \ int_ {0} ^ {a_ {rec}} c \ frac {da} {aH} $$

$$ H (a_ {rec}) = H (z_ {rec}) = H_0 \ sqrt {\ Omega_ {m, 0}} a ^ {- 3/2} $$

Während der Recombination period universewar Materie dominiert. dhΩrad << Ωmatter. Daher wird der Begriff Strahlung gestrichen.

$$ r_H (z_ {rec}) = \ frac {c} {H_0 \ sqrt {\ Omega_ {m, 0}}} \ int_ {0} ^ {a_ {rec}} \ frac {da} {a ^ { -1/2}} $$

$$ r_H (z_ {rec}) = \ frac {2c} {3H_0 \ sqrt {\ Omega_ {m, 0}}} \ frac {1} {(1 + z_ {rec}) ^ {3/2}} $$

$$ \ theta_H (rec) = \ frac {r_H (z_ {rec})} {d_A (z_ {rec})} $$

Das entspricht 0,5 Grad, wenn wir alle bekannten Werte in die Gleichung einfügen.

Das Electromagnetic radiationist von der Oberfläche der letzten Streuung undurchsichtig. Zwei beliebige Punkte, die nicht am Horizont voneinander liegen, müssen nicht dieselben Eigenschaften haben. Es gibt also unterschiedliche Temperaturwerte.

Wir können zwei Punkte auf dieser Oberfläche erhalten, die sich nicht kreuzten, was bedeutet, dass sich das Universum an einem Punkt schneller ausdehnte als die Lichtgeschwindigkeit, die das Inflationsmodell für die Expansion darstellt.

Punkte, die man sich merken sollte

• Die Horizontlänge ist die Entfernung, die Lichtphotonen von 'The Big Bang' bis 'The Recombination Era' zurücklegen.

• Während der Rekombinationsperiode war das Universum von Materie dominiert.

• Elektromagnetische Strahlung ist von der Oberfläche der letzten Streuung undurchsichtig.

Astrobiologyist das Studium von Ursprung, Evolution, Verteilung und Zukunft des Lebens im Universum. Es geht um das Entdecken und ErkennenExtrasolar Planets.

Astrobiology spricht die folgenden Punkte an -

• Wie beginnt und entwickelt sich das Leben? (Biologie + Geologie + Chemie + Atmosphärenwissenschaften)

• Gibt es Welten jenseits der Erde, die für das Leben günstig sind? (Astronomie)

• Was wäre die Zukunft des Lebens auf der Erde?

Astronomy spricht die folgenden Punkte an -

• Wie erkennt man das Planetensystem um andere Sterne?

• Eine der Methoden ist die direkte Bildgebung, aber es ist eine sehr schwierige Aufgabe, da Planeten im Vergleich zu Sternen extrem schwache Lichtquellen sind und das geringe Licht, das von ihnen kommt, in der Blendung ihres Elternsterns verloren geht.

• Der Kontrast ist besser, wenn der Planet näher an seinem Mutterstern und heiß ist, so dass er intensive Infrarotstrahlung aussendet. Wir können Bilder im Infrarotbereich machen.

Techniken zur Erkennung von extrasolaren Planeten

Die effizientesten Techniken zur Erkennung extrasolarer Planeten sind wie folgt. Jedes dieser Elemente wird auch in den folgenden Kapiteln ausführlich erläutert.

Radialgeschwindigkeitsmethode

Es wird auch als Doppler-Methode bezeichnet. In diesem -

• Das Sternplanetensystem dreht sich um ihren Schwerpunkt, Stern wackelt.

• Wackeln kann durch erkannt werden

  • Periodische Rot / Blau-Verschiebungen. Astrometrie - Messung der Objekte am Himmel sehr genau.

Transitmethode

Die Transitmethode (Kepler-Weltraumteleskop) wird verwendet, um die Größe herauszufinden. Im Gegensatz zu einem binären System ist der Helligkeitsabfall des Sterns durch den Planeten normalerweise sehr gering.

Direkte Bildgebung

Bildgebung des Planeten mit einem Teleskop.

Schauen wir uns eine Fallstudie zur Radialgeschwindigkeitsmethode an.

Fallstudie

Diese Fallstudie befindet sich auf der Kreisbahn und der Ebene der Umlaufbahn senkrecht zur Ebene des Himmels. Die Zeit, die beide um das Schwerpunktzentrum herum benötigen, ist gleich. Dies entspricht dem Zeitunterschied zwischen zwei Redshift- oder Blueshift-Werten.

Betrachten Sie das folgende Bild.

Bei A und C wird die volle Geschwindigkeit gemessen. Bei C ist die Geschwindigkeit Null.

• Vrmax = V _* ist die wahre Geschwindigkeit des Sterns.

• P ist die Zeitspanne des Sterns sowie des Planeten.

• θ ist die Umlaufphase.

• Sternmasse - M _* , Umlaufradius a _* , Planetenmassem_p.

Aus der Schwerpunktgleichung,

$$ m_p a_p = M_ \ ast a_ \ ast $$

Aus der Geschwindigkeitsgleichung,

$$ V_ \ ast = \ frac {2 \ pi a_ \ ast} {P} $$

$$ \ Rightarrow a_ \ ast = \ frac {PV_ \ ast} {2 \ pi} $$

Von Kepler’s Law,

$$ P ^ 2 = \ frac {4 \ pi ^ 2a_p ^ 3} {GM_ \ ast} $$

$$ \ Rightarrow a_p = \ left (\ frac {P ^ 2GM_ \ ast} {4 \ pi ^ 2} \ right) ^ {1/3} $$

Aus den obigen Gleichungen erhalten wir -

$$ \ Rightarrow m_p = \ left (\ frac {P} {2 \ pi G} \ right) ^ {1/3} M_ \ ast ^ {2/3} V_ \ ast $$

Wir erhalten: $ m_p, a_p $ und $ a_ \ ast $.

Die obige Gleichung ist auf die meisten massiven Planeten in der Nähe des Sterns ausgerichtet.

Punkte, die man sich merken sollte

• Astrobiologie ist das Studium von Ursprung, Evolution, Verteilung und Zukunft des Lebens im Universum.

• Techniken zum Erkennen der extrasolaren Planeten sind: Radialgeschwindigkeitsmethode, Transitmethode, direkte Bildgebung usw.

• Wackeln kann durch periodische Rot / Blau-Verschiebungen und Astrometrie erkannt werden.

• Die Radialgeschwindigkeitsmethode ist darauf ausgerichtet, massive Planeten in der Nähe des Sterns zu entdecken.

Im vorherigen Kapitel wurde die Radialgeschwindigkeitsmethode für den Fall, dass die Orbitalebene und die Himmelsebene senkrecht stehen, für Kreisbahnen diskutiert. Hier beschäftigen wir uns mit einem weiteren Fall, in dem die Orbitalebene und die Himmelsebene für Kreisbahnen nicht senkrecht sind.

Wenn sich die Orbitalebene in einem Winkel zur Himmelsebene befindet (nicht senkrecht), haben wir die folgende Situation:

In diesem Fall hatten wir, wenn sie senkrecht standen, zwei Punkte, an denen wir die wahre Geschwindigkeit messen konnten. Aber hier ist das nicht möglich. An allen Punkten können wir nur eine Komponente der wahren Geschwindigkeit messen,v.

$$ v_r = v \: sin (i) cos (\ theta) $$

wo θist die Phase der Umlaufbahn, die eine zeitabhängige Größe ist. Der Neigungswinkeliist andererseits zeitunabhängig. Daher,

$$ (v_r) _ {max} = v \: sin (i) $$

Die beobachtete Radialgeschwindigkeitskurve hat die folgende Form:

Wenn die Orbitalebene senkrecht zum Himmel steht -

$$ m_p = \ left (\ frac {P} {2 \ pi G} \ right) ^ {\ frac {1} {3}} (M_ \ ast) ^ {\ frac {2} {3}} v $ $

wo m_p, P, G, M∗sind die Masse des Planeten, die Umlaufzeit, die universelle Gravitationskonstante und die Masse des Sterns. In diesem Fall sollten wir es jedoch wie folgt ändern:

$$ m_psin (i) = \ left (\ frac {P} {2 \ pi G} \ right) ^ {\ frac {1} {3}} (M_ \ ast) ^ {\ frac {2} {3} } (v_r) _ {max} $$

Aber den Wert von i zu finden, ist eine schwierige Aufgabe. Wir können dem Wert von bestimmte Einschränkungen auferlegenimit Transitmethode. Der Durchgang des Planeten zwischen Stern und Erde wird als Transit bezeichnet. Wir können die Lichtkurve erhalten, indem wir einen Transit beobachten, und ein signifikanter Abfall des beobachteten Flusses einer Lichtkurve impliziert, dass i nahe bei 90 Grad liegt. Wenn solche Bedingungen nicht erfüllt sind, können wir keine Vorstellung vom Wert von habeni. Dann ist der Wert vonm_p dass wir finden, kann als Untergrenze für die Masse des Planeten dienen, da es tatsächlich ist m_p sin(i) und sin(i) ≤ 1.

Zusammenfassend lässt sich sagen, dass die Radialgeschwindigkeitsmethode bequemer ist als die Transitmethode, da die Radialgeschwindigkeit jederzeit gemessen werden kann, Transitmessungen jedoch nur während des Transits durchgeführt werden können, der möglicherweise nicht lange dauert.

Punkte, die man sich merken sollte

• Das Finden der Neigung der Umlaufbahn des Planeten wird durch die Radialgeschwindigkeitsmethode nicht erreicht.

• Die Radialgeschwindigkeitsmethode ist besser als die Transitmethode, da die Radialgeschwindigkeit im Gegensatz zu Transiten immer gemessen werden kann.

• Transite sind kurzlebig und sehr leicht zu übersehen.

Die Transitmethode (Kepler Space Telescope)wird verwendet, um die Größe herauszufinden. Der Helligkeitsabfall eines Sterns durch einen Planeten ist normalerweise weniger als bei einem binären System.

• F₀ ist der Fluss des Sterns, bevor der Planet ihn verdeckt.

• F₁ ist der Fluss, nachdem sich der gesamte Planet vor dem Stern befindet.

Das folgende Bild wird für alle Berechnungen verwendet.

$$ \ frac {F_0 - F_1} {F_0} = \ frac {\ pi r_p ^ {2}} {\ pi R ^ 2_ \ ast} $$

$$ \ frac {\ Delta F} {F} \ cong \ frac {r ^ 2_p} {R ^ 2_ \ ast} $$

$$ \ left (\ frac {\ Delta F} {F} \ right) _ {earth} \ cong 0,001 \% $$

$$ \ left (\ frac {\ Delta F} {F} \ right) _ {jupiter} \ cong 1 \% $$

Dies ist mit einem Bodenteleskop nicht einfach zu erreichen. Dies wird durch das Hubble-Teleskop erreicht.

Hier ist $ t_T $ die Zeit zwischen Position A und D und $ t_F $ ist die Zeit zwischen Position B und C.

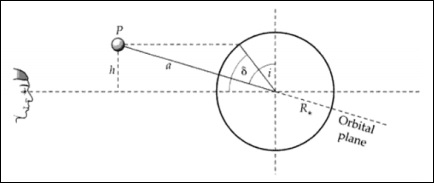
Die Geometrie eines Transits in Bezug auf die Neigung ivom System. Transitbreite und Neigung sind austauschbar.

Aus den obigen Bildern können wir schreiben -

$$ \ frac {h} {a} = cos (i) $$

$$ \ frac {h} {R_ \ ast} = sin (\ delta) $$

$$ cos (i) = \ frac {R_ \ ast sin (\ delta)} {a} $$

$$ y ^ 2 = (R_ \ ast + R_p) ^ 2 - h ^ 2 $$

$$ y = [(R_ \ ast + R_p) ^ 2 - h ^ 2] ^ {\ frac {1} {2}} $$

$$ sin (\ theta) = \ frac {y} {a} $$

$$ \ theta = sin ^ {- 1} \ left [\ frac {(R_ \ ast + R_p) ^ 2 - a ^ 2cos ^ 2 (i)} {a ^ 2} \ right] ^ {\ frac {1 } {2}} $$

$$ t_T = \ frac {P} {2 \ pi} \ times 2 \ theta $$

Hier ist $ t_T $ der Bruchteil eines Zeitraums, für den der Transit stattfindet, und (2θ / 2π) ist der Bruchteil des Winkels, für den der Transit stattfindet.

$$ sin (\ frac {t_T \ pi} {P}) = \ frac {R_ \ ast} {a} \ left [\ left (1+ \ frac {R_p} {R_ \ ast} \ right) ^ 2 - \ left (\ frac {a} {R_ \ ast} cos (i) \ right) ^ 2 \ right] ^ {\ frac {1} {2}} $$

Normalerweise ist ein >> R ∗ >> Rp. Also können wir schreiben -

$$ sin (\ frac {t_T \ pi} {P}) = \ frac {R_ \ ast} {a} \ left [1- \ left (\ frac {a} {R_ \ ast} cos (i) \ right ) ^ 2 \ right] ^ {\ frac {1} {2}} $$

Hier, Pist die Dauer zwischen zwei aufeinanderfolgenden Durchgängen. Die Transitzeit ist im Vergleich zur Umlaufzeit sehr viel kürzer. Daher,

$$ t_T = \ frac {P} {\ pi} \ left [\ left (\ frac {R_ \ ast} {a} \ right) ^ 2 - cos ^ 2 (i) \ right] ^ {\ frac {1 } {2}} $$

Hier, t_T, P, R∗ sind die Observablen, a und i sollte herausgefunden werden.

Jetzt,

$$ sin (\ frac {t_F \ pi} {P}) = \ frac {R_ \ ast} {a} \ left [\ left (1 - \ frac {R_p} {R_ \ ast} \ right) ^ 2 - \ left (\ frac {a} {R_ \ ast} cos \: i \ right) ^ 2 \ right] ^ {\ frac {1} {2}} $$

wobei $ y ^ 2 = (R_ \ ast - R_p) ^ 2 - h ^ 2 $.

Lassen,

$$ \ frac {\ Delta F} {F} = D = \ left (\ frac {R_p} {R_ \ ast} \ right) ^ 2 $$

Jetzt können wir ausdrücken,

$$ \ frac {a} {R_ \ ast} = \ frac {2P} {\ pi} D ^ {\ frac {1} {4}} (t ^ 2_T - t ^ 2_F) ^ {- \ frac {1 } {2}} $$

Für die Hauptreihensterne

$$ R_ \ ast \ propto M ^ \ alpha_ \ ast $$

$$ \ frac {R_ \ ast} {R_0} \ propto \ left (\ frac {M_ \ ast} {M_0} \ right) ^ \ alpha $$

Das gibt R∗.

Daher erhalten wir auch den Wert von 'a'.

Also bekommen wir 'R _p ', 'ap' und sogar 'i'.

Für all das,

$$ h \ leq R_ \ ast + R_p $$

$$ a \: cos \: i \ leq R_ \ ast + R_p $$

Selbst bei ~ 89 Grad ist die Transitdauer sehr gering. Der Planet muss sehr nahe sein, um eine ausreichende Transitzeit zu erhalten. Dies gibt eine enge Einschränkung für 'i'. Sobald wir 'i' erhalten, können wir 'm _p ' aus der Radialgeschwindigkeitsmessung ableiten .

Diese Erkennung durch das Transitverfahren wird als Zufallserkennung bezeichnet, dh als Wahrscheinlichkeit, einen Transit zu beobachten. Die Berechnungen der Transitwahrscheinlichkeit (Beobachtungswahrscheinlichkeit) sind nachstehend aufgeführt.

Die Transitwahrscheinlichkeit hängt mit dem Raumwinkel zusammen, der durch die beiden extremen Transitkonfigurationen verfolgt wird, nämlich -

$$ Festkörper \: Winkel \: von \: Planet \: = 2 \ pi \ left (\ frac {2R_ \ ast} {a} \ right) $$

Sowie der gesamte Raumwinkel an einer Semi-Major-Achse a oder -

$$ Festkörper \: Winkel \: von \: Kugel \: = \: 4 \ pi $$

Die Wahrscheinlichkeit ist das Verhältnis dieser beiden Bereiche -

$$ = \: \ frac {Fläche \: von \: Himmel \: bedeckt \: von \: günstige \: Ausrichtung} {Fläche \: von \: Himmel \: bedeckt \: von \: all \: möglich \: Ausrichtung \: von \: Umlaufbahn} $$

$ = \ frac {4 \ pi a_pR_ \ ast} {4 \ pi a ^ 2_p} = \ frac {R_ \ ast} {a_p} $ $ \ frac {area \: of \: hollow \: cyclinder} {area \ : von \: Kugel} $

Diese Wahrscheinlichkeit ist unabhängig vom Beobachter.

Punkte, die man sich merken sollte

• Die Transitmethode (Kepler Space Telescope) wird verwendet, um die Größe herauszufinden.
• Die Erkennung durch die Transitmethode ist eine zufällige Erkennung.
• Der Planet muss sehr nahe sein, um eine ausreichende Transitzeit zu erhalten.
• Die Transitwahrscheinlichkeit hängt mit dem Raumwinkel des Planeten zusammen.
• Diese Wahrscheinlichkeit ist unabhängig vom Bezugsrahmen des Beobachters.

Das erste direkte Bild eines extrasolaren Planeten im Jahr 2004 war von einem Massenplaneten 3-10 M_jupiter Umlauf um einen Braunen Zwerg (2M1207) mit einer Masse von 25 M_jupiter. Techniken wie Radialgeschwindigkeit, Transit, Gravitationsmikrolinse, Bildgebung, Astrometrie usw. wurden zum Nachweis von Exoplaneten verwendet. Die Anzahl der Erkennungen hat von Jahr zu Jahr zugenommen.

Bis etwa 2010 wurde die Radialgeschwindigkeitsmethode ausgiebig verwendet, jetzt werden die meisten Erkennungen mit der Transit-Methode durchgeführt. Die Anzahl der Entdeckungen stieg 2014 zu diesem Zeitpunkt stark anKepler Space Telescope (KST) begann die Ergebnisse zu geben.

Eine Massenperiodenverteilung zeigt, dass die Radialgeschwindigkeitsmethode stärker auf die Erkennung massereicher Planeten mit einer größeren Periode ausgerichtet ist, während bei Verwendung der Transitmethode Planeten mit geringerer Periode nur wie im folgenden Bild gezeigt erkannt werden (mit freundlicher Genehmigung des NASA Exoplanet Archive). .

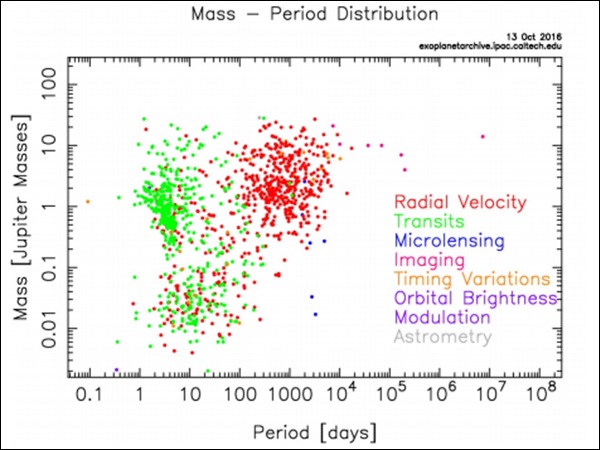
Seit dem Aufkommen von KST hat die Anzahl der Detektionen kleinerer Planeten massiv zugenommen. Dies geht aus der folgenden Abbildung hervor. Die von KST entdeckten Planeten sind in zwei Gruppen unterteilt: heiße massive Planeten, die als "heiße Jupiter" bezeichnet werden, und Planeten mit geringerer Masse, die als "heiße Supererden" bezeichnet werden (da sie massereicher als die Erde sind).

Wenn wir die Anzahl der detektierten extrasolaren Planeten gegen die Entfernung zu ihnen aufzeichnen, stellen wir fest, dass die meisten dieser Planeten innerhalb von 2 kpc liegen, was gut in unserer Galaxie liegt. Vielleicht sind die Planeten im Universum nicht so ungewöhnlich, da unsere Entdeckung nur auf bestimmte Arten von Planeten in einem sehr kleinen Teil des Universums beschränkt ist.

Planeten werden aus gebildet circumstellar disc oder proto planetary disc. Wenn Planeten während der Sternentstehung als Nebenprodukt entstehen, übersteigt die Anzahl der Planeten im Universum möglicherweise die Anzahl der Sterne im Universum !!

Bewohnbare Zonen

Eine bewohnbare Zone kann als die Zone um den Stern definiert werden, in der Wasser in flüssiger Form vorliegen kann. Betrachten Sie einen Planeten in der Entfernung $ a_p $ vom Stern, wie in der folgenden Abbildung gezeigt. Ein einfaches Verfahren zur Berechnung der Temperatur des Planeten wird wie folgt beschrieben.

$$ \ left (\ frac {L_ \ ast} {4 \ pi a ^ 2_p} \ right) \ pi R ^ 2_p (1 - A) = 4 \ pi R ^ 2_p \ sigma T ^ 4_p $$

und

$$ \ frac {L_ \ ast} {4 \ pi R ^ 2_ \ ast} = \ sigma T ^ 4_ \ ast $$

$$ \ also T_p = (1 - A) T_ \ ast \ sqrt {\ frac {R_ \ ast} {2a_p}} $$

In unserem Fall ersetzen

• L_sun = 3.83 x 10²⁶

• a_p = 1.5 ∗ 10¹¹ and

• A = 0.3

Gibt $ T_ {Earth} = 255K $. Die eigentliche Berechnung ist sehr aufwendig, einschließlich der Wolkenphysik. Die bewohnbare Zone in unserem Sonnensystem liegt zwischen 0,9 AU und 1,7 AU.

Es wurde festgestellt, dass die Leuchtkraft der Sonne aufgrund des abnehmenden Gasdrucks mit der Zeit zunimmt. Es war 30% weniger hell, als es anfing, Wasserstoff zu verbrennen. Dies würde zu einer Verschiebung der bewohnbaren Zone von der Sonne weg führen. Da sich die Erde nahe dem inneren Rand der bewohnbaren Zone befindet, wird sie sich vielleicht eines Tages aus der Zone herausbewegen!

Kontinuierlich bewohnbare Zone

Kurz gesagt wird es als bezeichnet CHZkann als der Bereich definiert werden, in dem flüssiges Wasser über die gesamte Lebensdauer der Hauptsequenz eines Sterns existieren kann. Das KST hat viele extrasolare Planeten entdeckt, die in der bewohnbaren Zone liegen.

Eine Biosignatur ist jede Substanz - wie ein Element, ein Isotop, ein Molekül oder ein Phänomen, das wissenschaftliche Beweise für das vergangene oder gegenwärtige Leben liefert. Ein Beispiel ist der Nachweis von O ₂ und CO ₂ auf einem Planeten, was normalerweise nicht allein durch geologische Prozesse möglich ist. Diese Detektion erfolgt durch Analyse der Absorptionsspektren.

Punkte, die man sich merken sollte

• Techniken wie Radialgeschwindigkeit, Transit, Gravitationsmikrolinse, Bildgebung, Astrometrie usw. wurden zum Nachweis von Exoplaneten verwendet.

• Die Radialgeschwindigkeitsmethode ist stärker auf die Erkennung massereicher Planeten mit größerer Periode ausgerichtet.

• Heiße massive Planeten werden "Hot Jupiters" genannt und Planeten mit geringerer Masse werden "Hot Super Earths" genannt.

• Die Anzahl der Planeten im Universum übersteigt die Anzahl der Sterne im Universum.

• Eine bewohnbare Zone kann als die Zone um den Stern definiert werden, in der Wasser in flüssiger Form vorliegen kann.