Konzept der Dimensionen

Wir werden uns dieses Beispiel ansehen, um das Konzept der Dimension zu verstehen.

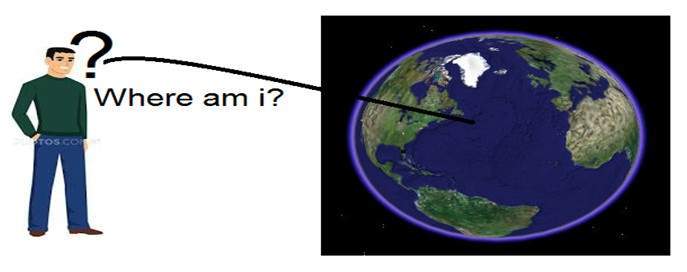
Stellen Sie sich vor, Sie haben einen Freund, der auf dem Mond lebt, und er möchte Ihnen ein Geschenk zu Ihrem Geburtstagsgeschenk schicken. Er fragt dich nach deinem Wohnsitz auf Erden. Das einzige Problem ist, dass der Kurierdienst auf dem Mond die alphabetische Adresse nicht versteht, sondern nur die numerischen Koordinaten. Wie schickst du ihm deine Position auf der Erde?

Hier kommt das Konzept der Dimensionen. Bemaßungen definieren die Mindestanzahl von Punkten, die erforderlich sind, um eine Position eines bestimmten Objekts innerhalb eines Raums zu bestimmen.

Kehren wir also noch einmal zu unserem Beispiel zurück, in dem Sie Ihre Position auf der Erde an Ihren Freund auf dem Mond senden müssen. Sie senden ihm drei Koordinatenpaare. Der erste heißt Längengrad, der zweite heißt Breitengrad und der dritte heißt Höhe.

Diese drei Koordinaten definieren Ihre Position auf der Erde. Die ersten beiden definieren Ihren Standort und die dritte definiert Ihre Höhe über dem Meeresspiegel.

Das bedeutet, dass nur drei Koordinaten erforderlich sind, um Ihre Position auf der Erde zu definieren. Das heißt, Sie leben in einer dreidimensionalen Welt. Und damit beantwortet dies nicht nur die Frage nach der Dimension, sondern auch den Grund, warum wir in einer 3D-Welt leben.

Da wir dieses Konzept in Bezug auf die digitale Bildverarbeitung untersuchen, werden wir dieses Konzept der Dimension nun mit einem Bild in Beziehung setzen.

Abmessungen des Bildes

Wenn wir also in der 3D-Welt leben, bedeutet dies eine dreidimensionale Welt. Was sind dann die Dimensionen eines Bildes, das wir erfassen? Ein Bild ist zweidimensional, deshalb definieren wir ein Bild auch als zweidimensionales Signal. Ein Bild hat nur Höhe und Breite. Ein Bild hat keine Tiefe. Schauen Sie sich dieses Bild unten an.

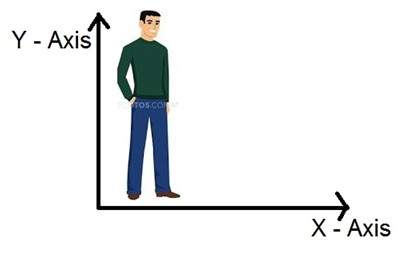
Wenn Sie sich die obige Abbildung ansehen, zeigt dies, dass sie nur zwei Achsen hat, nämlich die Höhen- und Breitenachse. Sie können die Tiefe dieses Bildes nicht wahrnehmen. Deshalb sagen wir, dass ein Bild ein zweidimensionales Signal ist. Unser Auge ist jedoch in der Lage, dreidimensionale Objekte wahrzunehmen. Dies wird jedoch im nächsten Tutorial zur Funktionsweise der Kamera und zur Wahrnehmung des Bildes näher erläutert.

Diese Diskussion führt zu einigen anderen Fragen, wie dreidimensionale Systeme aus zweidimensionalen Systemen gebildet werden.

Wie funktioniert Fernsehen?

Wenn wir das Bild oben betrachten, werden wir sehen, dass es ein zweidimensionales Bild ist. Um es in drei Dimensionen umzuwandeln, benötigen wir eine weitere Dimension. Nehmen wir Zeit als dritte Dimension. In diesem Fall verschieben wir dieses zweidimensionale Bild über die Zeit der dritten Dimension. Das gleiche Konzept wie im Fernsehen, mit dem wir die Tiefe verschiedener Objekte auf einem Bildschirm wahrnehmen können. Bedeutet das, dass das, was auf dem Fernseher kommt oder was wir auf dem Fernsehbildschirm sehen, 3D ist? Na das können wir ja.

Der Grund ist, dass wir im Falle des Fernsehens ein Video abspielen. Dann ist ein Video nichts anderes als zweidimensionale Bilder, die sich über die Zeitdimension bewegen. Da sich zweidimensionale Objekte über die dritte Dimension bewegen, die eine Zeit ist, können wir sagen, dass sie dreidimensional ist.

Unterschiedliche Dimensionen von Signalen

1-dimensionales Signal

Das übliche Beispiel für ein eindimensionales Signal ist eine Wellenform. Es kann mathematisch dargestellt werden als

F (x) = Wellenform

Wobei x eine unabhängige Variable ist. Da es sich um ein eindimensionales Signal handelt, wird nur eine Variable x verwendet.

Die bildliche Darstellung eines eindimensionalen Signals ist unten angegeben:

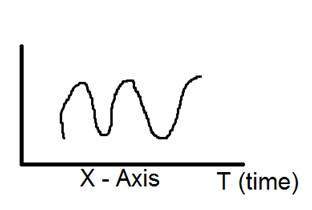
Die obige Abbildung zeigt ein eindimensionales Signal.

Dies führt nun zu einer anderen Frage: Obwohl es sich um ein eindimensionales Signal handelt, warum hat es dann zwei Achsen? Die Antwort auf diese Frage lautet: Obwohl es sich um ein eindimensionales Signal handelt, zeichnen wir es in einem zweidimensionalen Raum. Oder wir können sagen, dass der Raum, in dem wir dieses Signal darstellen, zweidimensional ist. Deshalb sieht es aus wie ein zweidimensionales Signal.

Vielleicht können Sie das Konzept einer Dimension besser verstehen, indem Sie sich die folgende Abbildung ansehen.

Beziehen Sie sich nun auf unsere anfängliche Diskussion über die Dimension. Betrachten Sie die obige Abbildung als eine reelle Linie mit positiven Zahlen von einem Punkt zum anderen. Wenn wir nun die Position eines Punktes auf dieser Linie erklären müssen, brauchen wir nur eine Zahl, was nur eine Dimension bedeutet.

2 Dimensionen Signal

Das übliche Beispiel eines zweidimensionalen Signals ist ein Bild, das bereits oben diskutiert wurde.

Wie wir bereits gesehen haben, ist ein Bild ein zweidimensionales Signal, dh es hat zwei Dimensionen. Es kann mathematisch dargestellt werden als:

F (x, y) = Bild

Wobei x und y zwei Variablen sind. Das Konzept der zweidimensionalen Dimension kann auch mathematisch wie folgt erklärt werden:

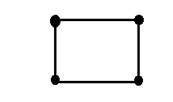
Beschriften Sie nun in der obigen Abbildung die vier Ecken des Quadrats als A, B, C bzw. D. Wenn wir ein Liniensegment in der Abbildung AB und die andere CD aufrufen, können wir sehen, dass sich diese beiden parallelen Segmente verbinden und ein Quadrat bilden. Jedes Liniensegment entspricht einer Dimension, daher entsprechen diese beiden Liniensegmente zwei Dimensionen.

3-dimensionales Signal

Das dreidimensionale Signal, wie es heißt, bezieht sich auf jene Signale, die drei Dimensionen haben. Das häufigste Beispiel wurde am Anfang diskutiert, das von unserer Welt ist. Wir leben in einer dreidimensionalen Welt. Dieses Beispiel wurde sehr ausführlich diskutiert. Ein anderes Beispiel für ein dreidimensionales Signal sind Würfel oder Volumendaten, oder das häufigste Beispiel wäre eine animierte oder 3D-Zeichentrickfigur.

Die mathematische Darstellung des dreidimensionalen Signals lautet:

F (x, y, z) = animiertes Zeichen.

Eine andere Achse oder Dimension Z ist an einer dreidimensionalen Dimension beteiligt, die die Illusion von Tiefe vermittelt. In einem kartesischen Koordinatensystem kann es wie folgt angesehen werden:

4-dimensionales Signal

In einem vierdimensionalen Signal sind vier Dimensionen beteiligt. Die ersten drei sind die gleichen wie bei dreidimensionalen Signalen: (X, Y, Z), und das vierte, das zu ihnen hinzugefügt wird, ist T (Zeit). Zeit wird oft als zeitliche Dimension bezeichnet, mit der Veränderungen gemessen werden können. Mathematisch kann ein 4-d-Signal wie folgt angegeben werden:

F (x, y, z, t) = Animationsfilm.

Das übliche Beispiel für ein 4-dimensionales Signal kann ein animierter 3D-Film sein. Da jede Figur eine 3D-Figur ist und sie dann in Bezug auf die Zeit bewegt werden, haben wir eine Illusion eines dreidimensionalen Films gesehen, der eher einer realen Welt ähnelt.

Das bedeutet, dass die Animationsfilme in Wirklichkeit 4-dimensional sind, dh: Bewegung von 3D-Zeichen über die Zeit der vierten Dimension.