Einführung in den Frequenzbereich

Wir haben mit Bildern in vielen Bereichen zu tun. Jetzt verarbeiten wir Signale (Bilder) im Frequenzbereich. Da es sich bei dieser Fourier-Reihe und dem Frequenzbereich ausschließlich um Mathematik handelt, werden wir versuchen, den Teil dieser Mathematik zu minimieren und uns mehr auf ihre Verwendung in DIP zu konzentrieren.

Frequenzbereichsanalyse

Bis jetzt analysieren wir alle Bereiche, in denen wir ein Signal analysiert haben, in Bezug auf die Zeit. Im Frequenzbereich analysieren wir das Signal jedoch nicht in Bezug auf die Zeit, sondern in Bezug auf die Frequenz.

Unterschied zwischen räumlichem Bereich und Frequenzbereich

Im räumlichen Bereich beschäftigen wir uns mit Bildern wie sie sind. Der Wert der Pixel des Bildes ändert sich in Bezug auf die Szene. Während wir uns im Frequenzbereich mit der Geschwindigkeit befassen, mit der sich die Pixelwerte im räumlichen Bereich ändern.

Sagen wir es der Einfachheit halber so.

Raumdomäne

Im einfachen räumlichen Bereich beschäftigen wir uns direkt mit der Bildmatrix. Während wir im Frequenzbereich ein Bild wie dieses behandeln.

Frequenzbereich

Wir transformieren zuerst das Bild in seine Häufigkeitsverteilung. Dann führt unser Black-Box-System die Verarbeitung aus, die es ausführen muss, und die Ausgabe der Black-Box ist in diesem Fall kein Bild, sondern eine Transformation. Nach der inversen Transformation wird es in ein Bild konvertiert, das dann im räumlichen Bereich betrachtet wird.

Es kann bildlich betrachtet werden als

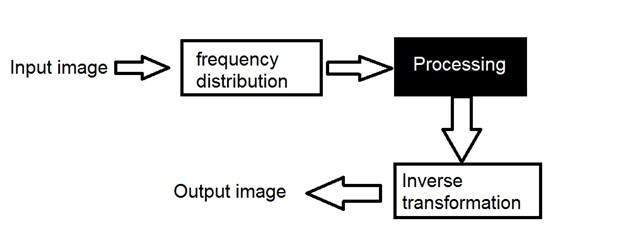
Hier haben wir das Wort Transformation verwendet. Was bedeutet das eigentlich?

Transformation

Ein Signal kann unter Verwendung mathematischer Operatoren, die als Transformationen bezeichnet werden, vom Zeitbereich in den Frequenzbereich umgewandelt werden. Es gibt viele Arten von Transformationen, die dies bewirken. Einige von ihnen sind unten angegeben.