Graustufentransformation

Wir haben einige der grundlegenden Transformationen in unserem Tutorial zur grundlegenden Transformation besprochen. In diesem Tutorial werden einige der grundlegenden Graustufentransformationen vorgestellt.

Bildverbesserung

Das Verbessern eines Bildes bietet einen besseren Kontrast und ein detaillierteres Bild im Vergleich zu nicht verbesserten Bildern. Die Bildverbesserung hat sehr viele Anwendungen. Es wird verwendet, um medizinische Bilder, Bilder, die mit Fernerkundung aufgenommen wurden, Bilder von Satelliten usw. Zu verbessern

Die Transformationsfunktion wurde unten angegeben

s = T (r)

Dabei ist r die Pixel des Eingabebildes und s die Pixel des Ausgabebildes. T ist eine Transformationsfunktion, die jeden Wert von r auf jeden Wert von s abbildet. Die Bildverbesserung kann durch Graustufentransformationen erfolgen, die unten erläutert werden.

Graustufentransformation

Es gibt drei grundlegende Graustufentransformationen.

Linear
Logarithmic
Machtgesetz

Das Gesamtdiagramm dieser Übergänge ist unten dargestellt.

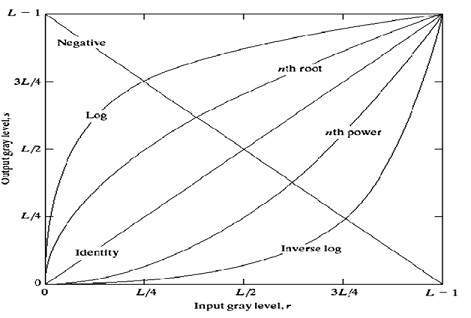
Lineare Transformation

Zuerst werden wir die lineare Transformation betrachten. Die lineare Transformation umfasst einfache Identität und negative Transformation. Die Identitätstransformation wurde in unserem Tutorial zur Bildtransformation erörtert, aber eine kurze Beschreibung dieser Transformation wurde hier gegeben.

Der Identitätsübergang wird durch eine gerade Linie dargestellt. Bei diesem Übergang wird jeder Wert des Eingabebildes direkt auf den Wert des Ausgabebilds abgebildet. Dies führt zu demselben Eingabebild und Ausgabebild. Und wird daher Identitätstransformation genannt. Es wurde unten gezeigt:

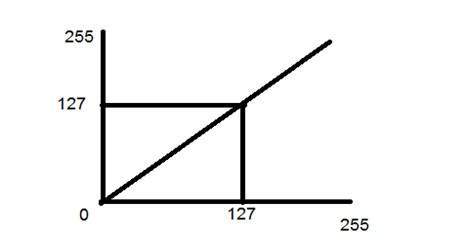
Negative Transformation

Die zweite lineare Transformation ist die negative Transformation, die die Identitätstransformation invertiert. Bei der negativen Transformation wird jeder Wert des Eingabebildes vom L-1 subtrahiert und auf das Ausgabebild abgebildet.

Das Ergebnis ist ungefähr so.

Bild eingeben

Ausgabebild

In diesem Fall wurde der folgende Übergang durchgeführt.

s = (L - 1) - r

Da das Eingabebild von Einstein ein 8-bpp-Bild ist, beträgt die Anzahl der Ebenen in diesem Bild 256. Wenn wir 256 in die Gleichung einfügen, erhalten wir dies

s = 255 - r

Jeder Wert wird also von 255 subtrahiert und das Ergebnisbild wurde oben gezeigt. Was also passiert ist, dass die helleren Pixel dunkel werden und das dunklere Bild hell wird. Und es ergibt sich ein negatives Bild.

Es wurde in der folgenden Grafik gezeigt.

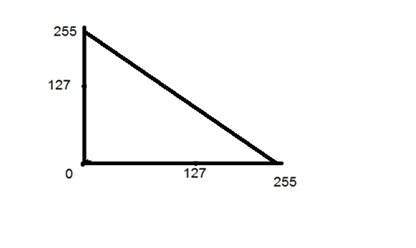
Logarithmische Transformationen

Die logarithmische Transformation enthält ferner zwei Arten der Transformation. Protokolltransformation und inverse Protokolltransformation.

Protokolltransformation

Die Protokolltransformationen können durch diese Formel definiert werden

s = c log (r + 1).

Wobei s und r die Pixelwerte der Ausgabe und des Eingabebildes sind und c eine Konstante ist. Der Wert 1 wird zu jedem Pixelwert des Eingabebildes addiert, da log (0) gleich unendlich ist, wenn das Bild eine Pixelintensität von 0 enthält. Also wird 1 addiert, um den Mindestwert auf mindestens 1 zu bringen.

Während der Protokolltransformation werden die dunklen Pixel in einem Bild im Vergleich zu den höheren Pixelwerten erweitert. Die höheren Pixelwerte werden bei der Protokolltransformation komprimiert. Dies führt zu folgender Bildverbesserung.

Der Wert von c in der Protokolltransformation passt die Art der gewünschten Verbesserung an.

Bild eingeben

Protokolltransformationsbild

Die inverse Protokolltransformation ist der Protokolltransformation entgegengesetzt.

Machtgesetztransformationen

Es gibt zwei weitere Transformationen, nämlich Potenzgesetztransformationen, die die n-te Potenz und die n-te Wurzeltransformation umfassen. Diese Transformationen können durch den Ausdruck gegeben werden:

s = cr ^ γ

Dieses Symbol γ heißt Gamma, weshalb diese Transformation auch als Gamma-Transformation bezeichnet wird.

Eine Variation des Wertes von γ variiert die Verbesserung der Bilder. Verschiedene Anzeigegeräte / Monitore haben ihre eigene Gammakorrektur, deshalb zeigen sie ihr Bild mit unterschiedlicher Intensität an.

Diese Art der Transformation wird zum Verbessern von Bildern für verschiedene Arten von Anzeigegeräten verwendet. Das Gamma verschiedener Anzeigegeräte ist unterschiedlich. Zum Beispiel liegt das Gamma der CRT zwischen 1,8 und 2,5, was bedeutet, dass das auf der CRT angezeigte Bild dunkel ist.