Bildtransformationen
Bevor wir diskutieren, was Bildtransformation ist, werden wir diskutieren, was eine Transformation ist.
Transformation
Transformation ist eine Funktion. Eine Funktion, die einen Satz nach dem Ausführen einiger Operationen einem anderen Satz zuordnet.
Digitales Bildverarbeitungssystem
Wir haben bereits in den einführenden Tutorials gesehen, dass wir in der digitalen Bildverarbeitung ein System entwickeln werden, dessen Eingabe ein Bild und dessen Ausgabe auch ein Bild wäre. Und das System würde eine gewisse Verarbeitung des Eingabebildes durchführen und seine Ausgabe als verarbeitetes Bild ausgeben. Es ist unten gezeigt.
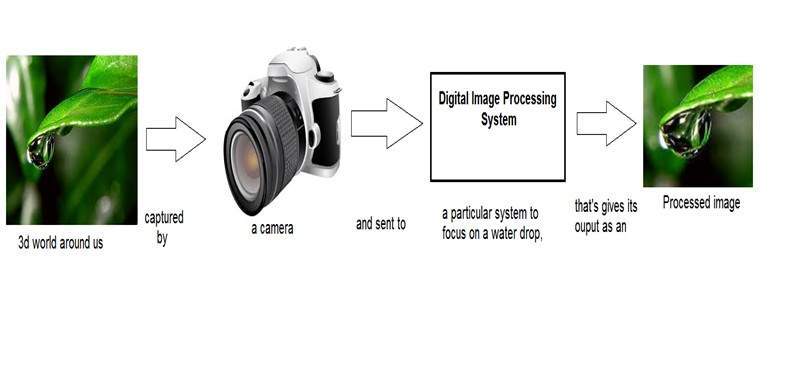
Die in diesem digitalen System angewendete Funktion, die ein Bild verarbeitet und in eine Ausgabe konvertiert, kann als Transformationsfunktion bezeichnet werden.
Wie es Transformation oder Beziehung zeigt, wie ein Bild1 in Bild2 konvertiert wird.
Bildtransformation.
Betrachten Sie diese Gleichung
G (x, y) = T {f (x, y)}
In dieser Gleichung
F (x, y) = Eingabebild, auf das die Transformationsfunktion angewendet werden muss.
G (x, y) = das Ausgabebild oder das verarbeitete Bild.
T ist die Transformationsfunktion.
Diese Beziehung zwischen dem Eingabebild und dem verarbeiteten Ausgabebild kann auch als dargestellt werden.
s = T (r)
Dabei ist r tatsächlich der Pixelwert oder die Graustufenintensität von f (x, y) an einem beliebigen Punkt. Und s ist der Pixelwert oder die Graustufenintensität von g (x, y) an jedem Punkt.
Die grundlegende Graustufentransformation wurde in unserem Tutorial zu grundlegenden Graustufentransformationen erläutert.
Jetzt werden wir einige der grundlegenden Transformationsfunktionen diskutieren.
Beispiele
Betrachten Sie diese Transformationsfunktion.
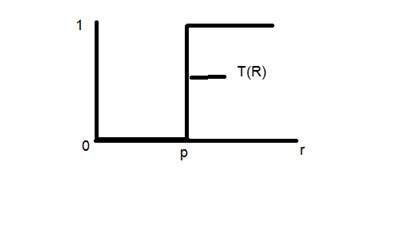
Nehmen wir an, dass der Punkt r 256 und der Punkt p 127 ist. Betrachten Sie dieses Bild als ein Bild mit einer Bpp. Das heißt, wir haben nur zwei Intensitätsstufen, die 0 und 1 sind. In diesem Fall kann die in der Grafik gezeigte Transformation als erklärt werden.
Alle Pixelintensitätswerte, die unter 127 (Punkt p) liegen, sind 0, bedeutet Schwarz. Und alle Pixelintensitätswerte, die größer als 127 sind, sind 1, das heißt Weiß. Aber genau am Punkt 127 gibt es eine plötzliche Änderung der Übertragung, so dass wir nicht sagen können, dass der Wert an diesem genauen Punkt 0 oder 1 wäre.
Mathematisch kann diese Transformationsfunktion bezeichnet werden als:
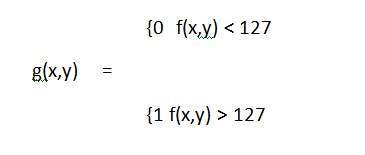
Betrachten Sie eine andere Transformation wie diese
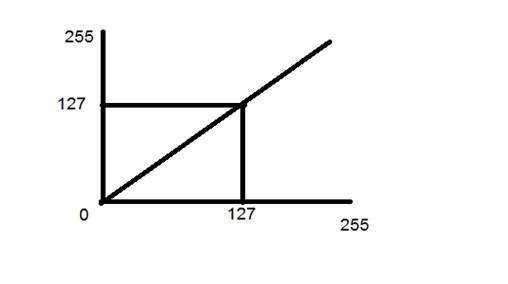
Wenn Sie sich nun dieses bestimmte Diagramm ansehen, sehen Sie eine gerade Übergangslinie zwischen Eingabebild und Ausgabebild.
Es zeigt, dass für jedes Pixel oder jeden Intensitätswert des Eingabebildes der gleiche Intensitätswert des Ausgabebildes vorliegt. Das heißt, das Ausgabebild ist eine exakte Nachbildung des Eingabebildes.
Es kann mathematisch dargestellt werden als:
g (x, y) = f (x, y)
Das Eingabe- und Ausgabebild wäre in diesem Fall unten dargestellt.
