Fourier-Reihe und Transformation

Im letzten Tutorial der Frequenzbereichsanalyse haben wir diskutiert, dass Fourier-Reihen und Fourier-Transformation verwendet werden, um ein Signal in einen Frequenzbereich umzuwandeln.

Fourier

Fourier war 1822 Mathematiker. Er gab Fourier-Reihen und Fourier-Transformationen an, um ein Signal in einen Frequenzbereich umzuwandeln.

Die Fourierreihe

Die Fourier-Reihe besagt einfach, dass periodische Signale in Summe von Sinus und Cosinus dargestellt werden können, wenn sie mit einem bestimmten Gewicht multipliziert werden. Ferner heißt es, dass periodische Signale mit den folgenden Eigenschaften in weitere Signale zerlegt werden können.

Die Signale sind Sinus und Cosinus
Die Signale sind Harmonische voneinander

Es kann bildlich betrachtet werden als

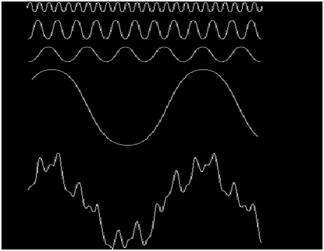
In dem obigen Signal ist das letzte Signal tatsächlich die Summe aller obigen Signale. Dies war die Idee des Fourier.

Wie es berechnet wird

Da, wie wir im Frequenzbereich gesehen haben, um ein Bild im Frequenzbereich zu verarbeiten, müssen wir es zuerst mit in den Frequenzbereich konvertieren und die Ausgabe invers nehmen, um es wieder in den räumlichen Bereich zu konvertieren. Deshalb haben sowohl die Fourier-Reihe als auch die Fourier-Transformation zwei Formeln. Eine zur Konvertierung und eine zur Konvertierung zurück in den räumlichen Bereich.

die Fourierreihe

Die Fourier-Reihe kann mit dieser Formel bezeichnet werden.

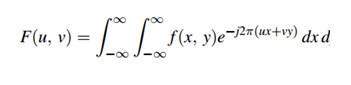
Die Umkehrung kann nach dieser Formel berechnet werden.

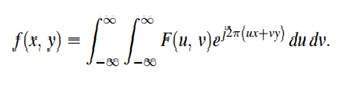
Fourier-Transformation

Die Fourier-Transformation besagt einfach, dass die nichtperiodischen Signale, deren Fläche unter der Kurve endlich ist, auch nach Integration mit einem bestimmten Gewicht in Integrale der Sinus- und Cosinuswerte dargestellt werden können.

Die Fourier-Transformation hat viele breite Anwendungen, einschließlich Bildkomprimierung (z. B. JPEG-Komprimierung), Filterung und Bildanalyse.

Unterschied zwischen Fourierreihen und Transformation

Obwohl sowohl die Fourier-Reihe als auch die Fourier-Transformation durch Fourier gegeben sind, besteht der Unterschied zwischen ihnen darin, dass die Fourier-Reihe auf periodische Signale angewendet wird und die Fourier-Transformation auf nicht periodische Signale angewendet wird

Welches wird auf Bilder angewendet

Die Frage ist nun, welche auf die Bilder, die Fourier-Reihe oder die Fourier-Transformation angewendet wird. Nun, die Antwort auf diese Frage liegt in der Tatsache, was Bilder sind. Bilder sind nicht periodisch. Und da die Bilder nicht periodisch sind, wird die Fourier-Transformation verwendet, um sie in den Frequenzbereich umzuwandeln.

Diskrete Fourier-Transformation

Da es sich um Bilder und tatsächlich um digitale Bilder handelt, werden wir für digitale Bilder an einer diskreten Fourier-Transformation arbeiten

Betrachten Sie den obigen Fourier-Term einer Sinuskurve. Es enthält drei Dinge.

Raumfrequenz
Magnitude
Phase

Die räumliche Frequenz hängt direkt mit der Helligkeit des Bildes zusammen. Die Größe der Sinuskurve hängt direkt mit dem Kontrast zusammen. Der Kontrast ist der Unterschied zwischen maximaler und minimaler Pixelintensität. Phase enthält die Farbinformationen.

Die Formel für die zweidimensionale diskrete Fourier-Transformation ist unten angegeben.

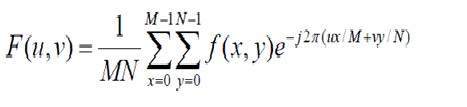
Die diskrete Fourier-Transformation ist eigentlich die abgetastete Fourier-Transformation, daher enthält sie einige Samples, die ein Bild bezeichnen. In der obigen Formel bezeichnet f (x, y) das Bild und F (u, v) bezeichnet die diskrete Fourier-Transformation. Die Formel für die zweidimensionale inverse diskrete Fourier-Transformation ist unten angegeben.

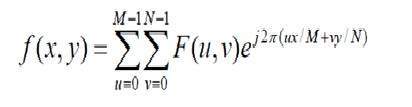
Die inverse diskrete Fourier-Transformation wandelt die Fourier-Transformation zurück in das Bild um

Betrachten Sie dieses Signal

Jetzt sehen wir ein Bild, dessen FFT-Betragsspektrum und dann verschobenes FFT-Betragsspektrum berechnet werden, und dann nehmen wir Log dieses verschobenen Spektrums.