Hochpass- und Tiefpassfilter

Im letzten Tutorial werden Filter kurz besprochen. In diesem Tutorial werden wir ausführlich darüber diskutieren. Bevor wir darüber sprechen, lassen Sie uns zuerst über Masken sprechen. Das Konzept der Maske wurde in unserem Tutorial zu Faltung und Masken erörtert.

Unscharfe Masken gegen abgeleitete Masken

Wir werden einen Vergleich zwischen Unschärfemasken und abgeleiteten Masken durchführen.

Unscharfe Masken

Eine Unschärfemaske hat die folgenden Eigenschaften.

Alle Werte in Unschärfemasken sind positiv
Die Summe aller Werte ist gleich 1
Der Kanteninhalt wird durch Verwendung einer Unschärfemaske reduziert
Mit zunehmender Größe der Maske tritt ein stärkerer Glättungseffekt auf

Derivative Masken

Eine abgeleitete Maske hat die folgenden Eigenschaften.

Eine abgeleitete Maske hat sowohl positive als auch negative Werte
Die Summe aller Werte in einer Ableitungsmaske ist gleich Null
Der Kanteninhalt wird durch eine abgeleitete Maske erhöht
Mit zunehmender Größe der Maske wird der Kanteninhalt erhöht

Beziehung zwischen Unschärfemaske und Ableitungsmaske mit Hochpassfiltern und Tiefpassfiltern.

Die Beziehung zwischen Unschärfemaske und Ableitungsmaske mit einem Hochpassfilter und einem Tiefpassfilter kann einfach definiert werden als.

Unschärfemasken werden auch als Tiefpassfilter bezeichnet
Derivative Masken werden auch als Hochpassfilter bezeichnet

Hochpassfrequenzkomponenten und Tiefpassfrequenzkomponenten

Die Hochpassfrequenzkomponenten bezeichnen Kanten, während die Tiefpassfrequenzkomponenten glatte Bereiche bezeichnen.

Ideale Tiefpass- und ideale Hochpassfilter

Dies ist das übliche Beispiel für Tiefpassfilter.

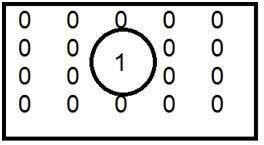
Wenn eins drinnen und die Null draußen platziert wird, erhalten wir ein unscharfes Bild. Wenn wir nun die Größe von 1 erhöhen, wird die Unschärfe erhöht und der Kanteninhalt verringert.

Dies ist ein häufiges Beispiel für ein Hochpassfilter.

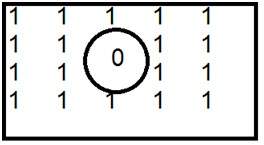
Wenn 0 im Inneren platziert wird, erhalten wir Kanten, wodurch wir ein skizziertes Bild erhalten. Ein ideales Tiefpassfilter im Frequenzbereich ist unten angegeben.

Das ideale Tiefpassfilter kann grafisch dargestellt werden als

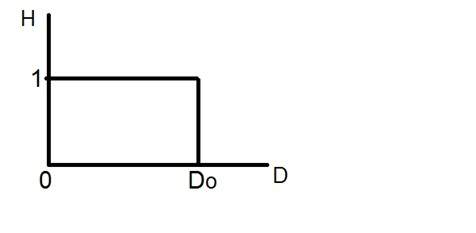
Wenden wir diesen Filter nun auf ein tatsächliches Bild an und sehen, was wir haben.

Beispielbild

Bild im Frequenzbereich

Anwenden eines Filters auf dieses Bild

Resultierendes Bild

Auf die gleiche Weise kann ein idealer Hochpassfilter auf ein Bild angewendet werden. Aber offensichtlich wären die Ergebnisse unterschiedlich, da der Tiefpass den Kanteninhalt verringert und der Hochpass ihn erhöht.

Gaußscher Tiefpass und Gaußscher Hochpassfilter

Gaußscher Tiefpass und Gaußscher Hochpassfilter minimieren das Problem, das bei idealen Tiefpass- und Hochpassfiltern auftritt.

Dieses Problem wird als Klingeleffekt bezeichnet. Dies liegt an der Vernunft, da an einigen Stellen der Übergang zwischen einer Farbe und der anderen nicht genau definiert werden kann, wodurch der Klingeleffekt an diesem Punkt auftritt.

Schauen Sie sich diese Grafik an.

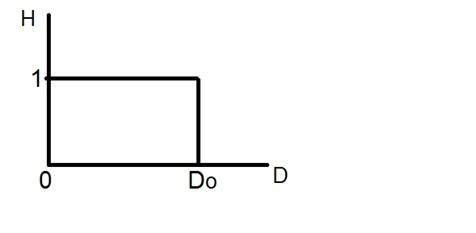
Dies ist die Darstellung eines idealen Tiefpassfilters. Jetzt können Sie genau am Punkt von Do nicht sagen, dass der Wert 0 oder 1 sein würde. Aufgrund dessen erscheint der Klingeleffekt an diesem Punkt.

Um den Effekt zu reduzieren, der als idealer Tiefpass und idealer Hochpassfilter erscheint, wird das folgende Gaußsche Tiefpassfilter und Gaußsche Hochpassfilter eingeführt.