कॉस्मोलॉजी - त्वरित गाइड
Cosmologyब्रह्मांड का अध्ययन है। समय में वापस ट्रेसिंग, ब्रह्मांड की उत्पत्ति के बारे में विचारों के कई स्कूल थे। कई विद्वानों का मानना थाSteady State Theory। इस सिद्धांत के अनुसार, ब्रह्मांड हमेशा एक ही था, इसकी कोई शुरुआत नहीं थी।
जबकि उन लोगों का एक समूह था जिन पर विश्वास था Big Bang Theory। यह सिद्धांत ब्रह्मांड की शुरुआत की भविष्यवाणी करता है। बिग बैंग से गर्म बचे हुए विकिरण के सबूत थे, जो फिर से मॉडल का समर्थन करता है। बिग बैंग थ्योरी ब्रह्मांड में प्रकाश तत्वों की प्रचुरता की भविष्यवाणी करती है। इस प्रकार, बिग बैंग के प्रसिद्ध मॉडल के बाद, हम बता सकते हैं कि ब्रह्मांड की शुरुआत थी। हम एक विस्तारित ब्रह्मांड में रह रहे हैं।
हबल रेडशिफ्ट
1900 की शुरुआत में, अत्याधुनिक दूरबीन, Mt Wilson, 100 इंच की दूरबीन, तब की सबसे बड़ी दूरबीन थी। हबल एक प्रमुख वैज्ञानिक थे, जिन्होंने उस दूरबीन के साथ काम किया था। उन्होंने पाया कि आकाशगंगा के बाहर आकाशगंगाएँ थीं।Extragalactic Astronomyकेवल 100 साल पुराना है। माउंट विल्सन सबसे बड़ा दूरबीन था जब तक कि पामर वेधशाला का निर्माण नहीं किया गया था जिसमें 200 इंच का दूरबीन था।
Hubbleमिल्की वे के बाहर आकाशगंगाओं का निरीक्षण करने वाला एकमात्र व्यक्ति नहीं था, हमासन ने उसकी मदद की। उन्होंने आस-पास की आकाशगंगाओं के स्पेक्ट्रा को मापने का काम किया। उन्होंने तब देखा कि एक गैलेक्टिक स्पेक्ट्रम निरंतर उत्सर्जन के साथ दृश्यमान तरंगदैर्ध्य रेंज में था। सातत्य के ऊपर उत्सर्जन और अवशोषण रेखाएँ थीं। इन रेखाओं से, हम अनुमान लगा सकते हैं कि क्या आकाशगंगा हमसे दूर या हमारी ओर बढ़ रही है।
जब हमें एक स्पेक्ट्रम मिलता है, तो हम मानते हैं कि सबसे मजबूत रेखा से आ रही है H-α। साहित्य से, सबसे मजबूत रेखा पर होना चाहिए6563 Å, लेकिन अगर रेखा कहीं आसपास होती है 7000Å, हम आसानी से कह सकते हैं कि यह नया रूप है।
वहाँ से Special Theory of Relativity,
$$1 + z = \sqrt{\frac{1+\frac{v}{c}}{1-\frac{v}{c}}}$$
जहाँ, Z रेडशिफ्ट है, एक आयाम रहित संख्या है और v मंदी का वेग है।
$$\frac{\lambda_{obs}}{\lambda_{rest}} = 1 + z$$
हबल और हमासन नीचे सूचीबद्ध हैं 22 Galaxiesउनके कागज में। लगभग इन सभी आकाशगंगाओं ने रेडशिफ्ट का प्रदर्शन किया। उन्होंने वेग (किमी / एस) बनाम दूरी (एमपीसी) की साजिश रची। उन्होंने एक रेखीय प्रवृत्ति देखी और हबल ने अपने प्रसिद्ध कानून को निम्नानुसार रखा।
$$v_r = H_o d$$
यह है Hubble Redshift Distance Relationship। सबस्क्रिप्टrइंगित करता है कि विस्तार रेडियल दिशा में है। जबकि,$v_r$ आवर्ती वेग है, $H_o$ हबल पैरामीटर है, dहमसे आकाशगंगा की दूरी है। यदि ब्रह्मांड के विस्तार की दर एक समान है, तो वे हमसे दूर की आकाशगंगाओं का तेजी से विकास करते हैं।
विस्तार
सब कुछ हमसे दूर होता जा रहा है। आकाशगंगा स्थिर नहीं हैं, हमेशा कुछ विस्तार हार्मोनिक है। हबल पैरामीटर की इकाइयां हैं किमी सेकंड -1 Mpc -1 । यदि कोई एक दूरी पर जाता है - 1 Mpc, आकाशगंगाएं 200 किलोमीटर / सेकंड की दर से आगे बढ़ रही होंगी। हबल पैरामीटर हमें विस्तार की दर देता है। हबल और हमसोन के अनुसार, का मान$H_o$ 200 किलोमीटर / सेकंड / एमसीपी है।
डेटा ने दिखाया कि सभी आकाशगंगाएं हमसे दूर जा रही हैं। इस प्रकार, यह स्पष्ट है कि हम ब्रह्मांड के केंद्र में हैं। लेकिन हबल ने यह गलती नहीं की, उसके अनुसार, हम जो भी आकाशगंगा में रहते हैं, हम अन्य सभी आकाशगंगाओं को हमसे दूर ले जाते हैं। इस प्रकार, निष्कर्ष यह है कि आकाशगंगाओं के बीच का स्थान विस्तृत है और ब्रह्मांड का कोई केंद्र नहीं है।
सब जगह विस्तार हो रहा है। हालांकि, कुछ ताकतें हैं जो विस्तार का विरोध कर रही हैं। रासायनिक बंधन, गुरुत्वाकर्षण बल और अन्य आकर्षक बल मिलकर वस्तुओं को पकड़ रहे हैं। पहले सभी वस्तुएँ एक साथ समीप थीं। बिग बैंग को एक आवेगी शक्ति के रूप में देखते हुए, इन वस्तुओं को एक दूसरे से दूर जाने के लिए निर्धारित किया जाता है।
समय का पैमाना
स्थानीय पैमानों पर, काइनेमेटिक्स गुरुत्वाकर्षण द्वारा शासित होता है। मूल हब्बल के नियम में, कुछ आकाशगंगाएँ थीं, जो नीली-पाली दिखाई देती थीं। इसे आकाशगंगाओं की संयुक्त गुरुत्वाकर्षण क्षमता का श्रेय दिया जा सकता है। हबल के नियम से गुरुत्वाकर्षण ने चीजों को नष्ट कर दिया है। एंड्रोमेडा गैलेक्सी हमारी ओर आ रहा है। गुरुत्वाकर्षण चीजों को धीमा करने की कोशिश कर रहा है। शुरू में विस्तार धीमा हो रहा था, अब यह तेजी से बढ़ रहा है।
वहाँ था एक Cosmic Jerkइसके कारण। हबल पैरामीटर के लिए कई अनुमान लगाए गए हैं। यह 90 वर्षों में 500 किलोमीटर / सेकंड / एमपीसी से 69 किलोमीटर / सेकंड / एमपीसी तक विकसित हुआ है। मूल्य में असमानता दूरी के कम होने के कारण थी। Cepheid Stars दूरी अंशशोधक के रूप में उपयोग किए गए थे, हालांकि विभिन्न प्रकार के सेफिड सितारे हैं और हबल पैरामीटर के अनुमान के लिए इस तथ्य पर विचार नहीं किया गया था।
हबल समय
हब्बल स्थिरांक हमें ब्रह्मांड की आयु का यथार्थवादी अनुमान देता है। $H_o$ब्रह्मांड की उम्र प्रदान करेगा बशर्ते आकाशगंगाएँ एक ही वेग से चलती रही हों। का विलोम$H_o$ हमें हबल समय देता है।
$$t_H = \frac{1}{H_o}$$
के वर्तमान मूल्य को प्रतिस्थापित करना $H_o, t_H$ = 14अरब वर्ष। विस्तार की दर ब्रह्मांड की शुरुआत के दौरान निरंतर रही है। भले ही यह सच न हो,$H_o$ब्रह्मांड की उम्र पर एक उपयोगी सीमा देता है। विस्तार की एक निरंतर दर को मानते हुए, जब हम दूरी और समय के बीच एक ग्राफ बनाते हैं, तो ग्राफ का ढलान वेग से दिया जाता है।
इस मामले में, हबल समय वास्तविक समय के बराबर है। हालांकि, यदि ब्रह्मांड अतीत में तेजी से विस्तार कर रहा था और वर्तमान में धीमा है, हबल समय ब्रह्मांड की आयु की एक ऊपरी सीमा देता है। यदि ब्रह्मांड पहले धीरे-धीरे विस्तार कर रहा था, और अब तेजी से बढ़ रहा है, तो हबल समय ब्रह्मांड की आयु पर एक कम सीमा देगा।
$t_H = t_{age}$ - यदि विस्तार की दर स्थिर है।
$t_H > t_{age}$ - यदि ब्रह्माण्ड अतीत में तेजी से विस्तारित हुआ है और वर्तमान में धीमा है।
$t_H < t_{age}$ - यदि ब्रह्माण्ड ने अतीत में धीमी गति से विस्तार किया है और वर्तमान में तेज है।
10 आकाशगंगाओं के एक समूह पर विचार करें जो आकाशगंगाओं के दूसरे समूह से 200 एमपीसी पर हैं। एक समूह के भीतर आकाशगंगा कभी निष्कर्ष नहीं निकालती है कि ब्रह्मांड का विस्तार हो रहा है क्योंकि एक स्थानीय समूह के भीतर कीनेमेटीक्स गुरुत्वाकर्षण द्वारा नियंत्रित होती है।
याद दिलाने के संकेत
कॉस्मोलॉजी हमारे ब्रह्मांड के भूत, वर्तमान और भविष्य का अध्ययन है।
हमारा ब्रह्मांड universe14 बिलियन वर्ष पुराना है।
ब्रह्मांड लगातार विस्तार कर रहा है।
हबल पैरामीटर ब्रह्मांड की आयु का एक माप है।
का वर्तमान मूल्य Ho 69 किलोमीटर / सेकंड / एमसीपी है।
बहुत लंबे समय तक, किसी ने भी आकाशगंगाओं को हमारे मिल्की वे के बाहर मौजूद नहीं माना। 1924 में, एडविन हबल ने पता लगायाCepheid’sएंड्रोमेडा नेबुला में और उनकी दूरी का अनुमान लगाया। उन्होंने निष्कर्ष निकाला कि ये "सर्पिल नेबुला" वास्तव में अन्य आकाशगंगाएं थीं और हमारे मिल्की वे का हिस्सा नहीं थीं। इसलिए, उन्होंने यह स्थापित किया कि M31 (एंड्रोमेडा गैलेक्सी) एक द्वीप ब्रह्मांड है। का जन्म थाExtragalactic Astronomy।
सेफिड का शो ए periodic dip in their brightness। टिप्पणियों से पता चलता है कि क्रमिक डिप्स के बीच की अवधि जिसे स्पंदन की अवधि कहा जाता है, चमक से संबंधित है। इसलिए, उन्हें दूरी संकेतक के रूप में उपयोग किया जा सकता है। सूर्य जैसे मुख्य अनुक्रम तारे हाइड्रोस्टैटिक संतुलन में हैं और वे अपने मूल में हाइड्रोजन को जलाते हैं। हाइड्रोजन पूरी तरह से जल जाने के बाद, तारे लाल विशालकाय चरण की ओर बढ़ते हैं और अपने संतुलन को फिर से हासिल करने की कोशिश करते हैं।
सेफिड स्टार्स मेन सीक्वेंस स्टार्स हैं जो मेन सीक्वेंस स्टार्स से रेड जायंट्स में ट्रांसफर कर रहे हैं।
सेफिड्स का वर्गीकरण
इन स्पंदित चर सितारों के 3 व्यापक वर्ग हैं -
Type-I Cepheids (या क्लासिकल सेफिड्स) - 30-100 दिनों की अवधि।
Type-II Cepheids (या डब्ल्यू वर्जिन स्टार्स) - 1-50 दिनों की अवधि।
RR Lyrae Stars - 0.1-1 दिन की अवधि।
उस समय, हबल को चर सितारों के इस वर्गीकरण के बारे में पता नहीं था। यही कारण है कि हब्बल स्थिरांक का अतिरेक था, जिसके कारण उसने हमारे ब्रह्मांड की कम आयु का अनुमान लगाया था। तो, मंदी के वेग को भी कम करके आंका गया था। सेफिड में, गड़बड़ी सितारे के केंद्र से बाहर की ओर रेडियल फैलती है जब तक कि नया संतुलन प्राप्त नहीं हो जाता।
चमक और धड़कन की अवधि के बीच संबंध
आइए अब हम इस तथ्य के भौतिक आधार को समझने की कोशिश करते हैं कि उच्च धड़कन की अवधि अधिक चमक का अर्थ है। चमकदार एल और मास एम के एक स्टार पर विचार करें।
हम जानते हैं कि -
$$L \propto M^\alpha$$
जहां कम द्रव्यमान सितारों के लिए α = 3 से 4।
वहाँ से Stefan Boltzmann Law, हम जानते हैं कि -
$$L \propto R^2 T^4$$
अगर R त्रिज्या है और $c_s$ ध्वनि की गति है, तो धड़कन की अवधि P के रूप में लिखा जा सकता है -
$$P = R/c_s$$
लेकिन तापमान के संदर्भ में किसी भी माध्यम से ध्वनि की गति को व्यक्त किया जा सकता है -
$$c_s = \sqrt{\frac{\gamma P}{\rho}}$$
यहाँ, γ isothermal मामलों के लिए 1 है।
एक आदर्श गैस के लिए, P = nkT, जहां k है Boltzmann Constant। तो, हम लिख सकते हैं -
$$P = \frac{\rho kT}{m}$$
कहाँ पे $\rho$ घनत्व और है m एक प्रोटॉन का द्रव्यमान है।
इसलिए, अवधि द्वारा दी गई है -
$$P \cong \frac{Rm^{\frac{1}{2}}}{(kT)^{{\frac{1}{2}}}}$$
Virial Theorem बताता है कि एक स्थिर, आत्म-गुरुत्वाकर्षण, समान द्रव्यमान वस्तुओं (जैसे सितारों, आकाशगंगाओं) के गोलाकार वितरण, कुल गतिज ऊर्जा के लिए k यह वस्तु कुल गुरुत्वाकर्षण क्षमता के आधे के बराबर माइनस है u, अर्थात,
$$u = -2k$$
आइए हम मान लें कि वायरल प्रमेय इन चर सितारों के लिए सही है। यदि हम तारे की सतह पर एक प्रोटॉन को सही मानते हैं, तो वायरल प्रमेय से हम कह सकते हैं -
$$\frac{GMm}{R} = mv^2$$
मैक्सवेल वितरण से,
$$v = \sqrt{\frac{3kT}{2}}$$
इसलिए, अवधि -
$$P \sim \frac{RR^{\frac{1}{2}}}{(GM)^{\frac{1}{2}}}$$
जो ये दर्शाता हे
$$P \propto \frac{R^{\frac{3}{2}}}{M^{\frac{1}{2}}}$$
हम जानते हैं कि - $M \propto L^{1/\alpha}$
भी $R \propto L^{1/2}$
के लिए β > 0, हम अंत में मिलता है - $P \propto L^\beta$
याद दिलाने के संकेत
सेफिड स्टार्स मेन सीक्वेंस स्टार्स हैं जो मेन सीक्वेंस स्टार्स से रेड जायंट्स में ट्रांसफर कर रहे हैं।
सिफिड 3 प्रकार के होते हैं: टाइप-आई, टाइप- II, आरआर-लाइरे में पल्सेटिंग अवधि के घटते क्रम में।
सेफिड की पल्सेटिंग अवधि इसकी चमक (चमक) के सीधे आनुपातिक है।
हबल की टिप्पणियों ने इस तथ्य का उपयोग किया कि रेडियल वेग का स्थानांतरण से संबंधित है Spectral Lines। यहां, हम चार मामलों का निरीक्षण करेंगे और पुनरावृत्ति वेग के बीच संबंध खोजेंगे ($v_r$) और रेड शिफ्ट (z)।
केस 1: स्रोत के गैर-सापेक्ष मामले
इस मामले में, v, c से बहुत कम है। स्रोत कुछ संकेत (ध्वनि, प्रकाश, आदि) उत्सर्जित कर रहा है, जो के रूप में प्रचारित कर रहा हैWavefronts। स्रोत फ्रेम में दो लगातार सिग्नल भेजने के बीच का समय अंतराल हैΔts। प्रेक्षक फ्रेम में दो लगातार संकेतों के स्वागत के बीच का समय अंतराल हैΔto।

यदि पर्यवेक्षक और स्रोत दोनों स्थिर हैं, तो Δts = butto, लेकिन यहाँ ऐसा नहीं है। इसके बजाय, संबंध इस प्रकार है।
$$\Delta t_o = \Delta t_s + \frac{\Delta l}{c}$$
अभी, $\Delta l = v \Delta t_s$
इसके अलावा, चूंकि (लहर की गति x समय) = तरंगदैर्ध्य, हमें मिलता है
$$\frac{\Delta t_o}{\Delta t_s} = \frac{\lambda_o}{\lambda_s}$$
उपरोक्त समीकरणों से, हमें निम्नलिखित संबंध मिलते हैं -
$$\frac{\lambda_o}{\lambda_s} = 1 + \frac{v}{c}$$
कहाँ पे $\lambda _s$ स्रोत पर संकेत की तरंग दैर्ध्य है और $\lambda _o$ पर्यवेक्षक द्वारा व्याख्या की गई संकेत की तरंग दैर्ध्य है।
यहां, चूंकि स्रोत पर्यवेक्षक से दूर जा रहा है, v सकारात्मक है।
लाल पारी -
$$z = \frac{\lambda_o - \lambda_s}{\lambda_s} = \frac{\lambda_o}{\lambda_s} - 1$$
उपरोक्त समीकरणों से, हमें निम्न प्रकार से लाल पारी मिलती है।
$$z = \frac{v}{c}$$
केस 2: ऑब्जर्वर मूव का नॉन-रिलेटिव केस
इस मामले में, v, c से बहुत कम है। यहाँ,$\Delta l$ फरक है।
$$\Delta l = v \Delta t_o$$

सरलीकरण पर, हम प्राप्त करते हैं -
$$\frac{\Delta t_o}{\Delta t_s} = \left ( 1 - \frac{v}{c} \right )^{-1}$$
हमें रेड शिफ्ट इस प्रकार है -
$$z = \frac{v/c}{1-v/c}$$
जबसे v << cकेस I और केस II दोनों के लिए लाल बदलाव की अभिव्यक्ति लगभग समान है।
आइए देखें कि उपरोक्त दो मामलों में प्राप्त लाल पारियां किस प्रकार भिन्न होती हैं।
$$z_{II} - z_I = \frac{v}{c} \left [ \frac{1}{1 - v/c}-1 \right ]$$
इसलिये, $z_{II} − z_{I}$ की वजह से एक बहुत छोटी संख्या है $(v/c)^2$ कारक।
इसका अर्थ है कि, यदि v << c, हम यह नहीं बता सकते कि स्रोत चल रहा है, या पर्यवेक्षक आगे बढ़ रहा है।
आइये अब समझते हैं Basics of STR (सापेक्षता का विशेष सिद्धांत) -
प्रकाश की गति एक स्थिर है।
जब स्रोत (या पर्यवेक्षक) प्रकाश की गति के बराबर गति के साथ आगे बढ़ रहा है, तो सापेक्ष प्रभाव देखे जाते हैं।
समय फैलाव: $\Delta t_o = \gamma \Delta t_s$
लंबाई संकुचन: $\Delta l_o = \Delta t_s/\gamma$
यहाँ, $\gamma$ है Lorrentz factor1 से अधिक।
$$\gamma = \frac{1}{\sqrt{1-(v^2/c^2)}}$$
केस 3: रिलेटिव केस ऑफ सोर्स मूविंग
इस मामले में, v, c की तुलना में है। केस I के समान आंकड़े का संदर्भ लें। सापेक्षता प्रभाव के कारण, समय का फैलाव देखा जाता है और इसलिए निम्नलिखित संबंध प्राप्त होता है। (स्रोत सापेक्ष गति के साथ बढ़ रहा है)
$$\Delta t_o = \gamma \Delta t_s + \frac{\Delta l}{c}$$
$$\Delta l = \frac{v\gamma \Delta t_s}{c}$$
$$\frac{\Delta t_o}{\Delta t_s} = \frac{1 + v/c}{\sqrt{1- (v^2/c^2)}}$$
आगे सरलीकरण पर, हम प्राप्त करते हैं,
$$1 + z = \sqrt{\frac{1+v/c}{1-v/c}}$$
उपरोक्त अभिव्यक्ति के रूप में जाना जाता है Kinematic Doppler Shift Expression।
केस 4: ऑब्जर्वर मूविंग के रिलेटिव केस
केस II में उसी आंकड़े का संदर्भ लें। सापेक्ष प्रभाव के कारण, समय की कमी देखी जाती है और इसलिए निम्नलिखित संबंध प्राप्त किया जाता है। (ऑब्जर्वर रिलेटिव स्पीड के साथ बढ़ रहा है)
$$\Delta t_o = \frac{\Delta t_s}{\gamma}+\frac{\Delta l}{c}$$
$$\Delta l = \frac{v\Delta t_o}{c}$$
$$\frac{\Delta t_o}{\Delta t_s} = \frac{\sqrt{1-( v^2/c^2)}}{1-v/c}$$
आगे सरलीकरण पर, हम प्राप्त करते हैं -
$$1 + z = \sqrt{\frac{1+ v/c}{1- v/c}}$$
उपरोक्त अभिव्यक्ति वही है जो हमें केस III के लिए मिली थी।
याद दिलाने के संकेत
एक तारे का पुनरावर्तन वेग और रेडशिफ्ट संबंधित मात्राएँ हैं।
एक गैर-सापेक्ष मामले में, हम यह निर्धारित नहीं कर सकते कि स्रोत चल रहा है या स्थिर।
एक सापेक्षतावादी मामले में, स्रोत या पर्यवेक्षक को स्थानांतरित करने के लिए रिडशिफ्ट-पुनरावर्तन वेग संबंध में कोई अंतर नहीं है।
मूविंग क्लॉक धीमी गति से चलती हैं, सापेक्षता सिद्धांत का प्रत्यक्ष परिणाम है।
एक आकाशगंगा जो रेडशिफ्ट पर है z = 10, से मेल खाती है v≈80% का c। मिल्की वे का द्रव्यमान लगभग है1011M⊙, अगर हम काले पदार्थ पर विचार करते हैं, तो यह है 1012M⊙। इस प्रकार हमारा दूधिया रास्ता बड़े पैमाने पर है। यदि यह 80% पर चलता हैc, यह सामान्य अवधारणा में फिट नहीं है कि वस्तुएं कैसे चलती हैं।
हम जानते है,
$$\frac{v_r}{c} = \frac{\lambda_{obs} - \lambda{rest}}{\lambda_{rest}}$$
Z के छोटे मूल्यों के लिए,
$$z = \frac{v_r}{c} = \frac{\lambda_{obs}-\lambda_{rest}}{\lambda_{rest}}$$
निम्नलिखित ग्राफ में, फ्लक्स और तरंग दैर्ध्य के बीच का वर्ग, निरंतरता के शीर्ष पर उत्सर्जन लाइनें हैं। वहाँ सेH-α लाइन की जानकारी, हम निष्कर्ष निकालते हैं कि मोटे तौर पर z = 7। इसका मतलब है कि आकाशगंगा 70% पर घूम रही हैc। हम एक बदलाव का अवलोकन कर रहे हैं और इसे वेग के रूप में व्याख्या कर रहे हैं। हमें इस धारणा से छुटकारा पाना चाहिए और देखना चाहिएzएक अलग तरीके से। ब्रह्मांड को दर्शाने वाले 2 डी ग्रिड के रूप में अंतरिक्ष की कल्पना करें जैसा कि नीचे दिखाया गया है।

काले तारे को हमारा अपना दूधिया रास्ता और नीले तारे को कुछ अन्य आकाशगंगा मानते हैं। जब हम इस आकाशगंगा से प्रकाश को रिकॉर्ड करते हैं, तो हम स्पेक्ट्रम को देखते हैं और इसके रेडशिफ्ट का पता लगाते हैं अर्थात आकाशगंगा दूर जा रही है। जब फोटॉन उत्सर्जित होता था, तो इसका सापेक्ष वेग होता था।
क्या होगा अगर अंतरिक्ष का विस्तार हो रहा था?
यह फोटॉन का एक तात्कालिक रेडशिफ्ट है। दो आकाशगंगाओं के बीच की जगह के साथ संचयी रेडशिफ्ट्स एक बड़े रेडशिफ्ट की ओर बढ़ेंगे। तरंगदैर्ध्य अंत में बदल जाएगा। यह आकाशगंगाओं की गतिज गति के बजाय अंतरिक्ष का विस्तार है।
निम्नलिखित छवि से पता चलता है कि यदि आपसी गुरुत्वाकर्षण का विस्तार होता है तो यह हबल के कानून में भाग नहीं ले रहा है।

किनेमेटिक डॉपलर शिफ्ट में, उत्सर्जन के समय फोटॉन में रेडशिफ्ट प्रेरित होता है। एक कॉस्मोलॉजिकल रेडशिफ्ट में, हर चरण में, यह संचयी रूप से पुनर्वितरित हो रहा है। गुरुत्वाकर्षण क्षमता में, एक फोटॉन नीले रंग में स्थानांतरित हो जाएगा। जैसे-जैसे यह गुरुत्वाकर्षण क्षमता से बाहर निकलता है, यह फिर से लाल हो जाता है।
सापेक्षतावाद के एक विशेष सिद्धांत के अनुसार, एक-दूसरे के पास से गुजरने वाली दो वस्तुओं में प्रकाश की गति से अधिक एक सापेक्ष वेग नहीं हो सकता है। हम जिस वेग की बात करते हैं, वह ब्रह्मांड के विस्तार का है। Z के बड़े मूल्यों के लिए, रेडशिफ्ट कॉस्मोलॉजिकल है और हमारे संबंध में ऑब्जेक्ट के वास्तविक पुनरावर्तन वेग का एक वैध उपाय नहीं है।
कॉस्मोलॉजिकल सिद्धांत
इससे उपजा है Copernicus Notionब्रह्माण्ड का। इस धारणा के अनुसार, ब्रह्मांड समरूप और समस्थानिक है। ब्रह्मांड में कोई पसंदीदा दिशा और स्थान नहीं है।
समरूपता का मतलब है कि आप ब्रह्मांड के किस भाग में रहते हैं, आप देखेंगे कि ब्रह्मांड सभी भागों में समान है। आइसोट्रोपिक प्रकृति का मतलब है कि आप किस दिशा में देखते हैं, आप एक ही संरचना को देखने जा रहे हैं।
समरूपता का एक उपयुक्त उदाहरण धान का खेत है। यह सभी भागों से सजातीय दिखता है, लेकिन जब हवा बहती है, तो इसके अभिविन्यास में भिन्नताएं होती हैं, इस प्रकार यह आइसोट्रोपिक नहीं है। समतल भूमि पर एक पर्वत पर विचार करें और एक पर्यवेक्षक पहाड़ की चोटी पर खड़ा है। वह समतल भूमि के समस्थानिक प्रकृति को देखेगा, लेकिन यह सजातीय नहीं है। यदि एक सजातीय ब्रह्मांड में, यह एक बिंदु पर आइसोट्रोपिक है, तो यह हर जगह आइसोट्रोपिक है।
ब्रह्मांड का मानचित्र बनाने के लिए बड़े पैमाने पर सर्वेक्षण हुए हैं। Sloan Digital Sky Surveyएक ऐसा सर्वेक्षण है, जिसमें घोषणा पर ज्यादा ध्यान नहीं दिया गया, लेकिन सही उदगम पर। लुकबैक का समय लगभग 2 बिलियन वर्ष है। प्रत्येक पिक्सेल एक आकाशगंगा के स्थान से मेल खाती है और रंग रूपात्मक संरचना से मेल खाती है। हरे रंग ने नीले सर्पिल आकाशगंगा का प्रतिनिधित्व किया, जबकि लाल झूठे रंग ने बड़े पैमाने पर आकाशगंगाओं का संकेत दिया।
ब्रह्माण्ड संबंधी वेब में एक रेशा संरचना में आकाशगंगाएँ होती हैं और आकाशगंगाओं के बीच में voids होते हैं।
$\delta M/M \cong 1$यानी, द्रव्यमान वितरण का उतार-चढ़ाव 1 M है, किसी दिए गए घन के भीतर मौजूद पदार्थ का द्रव्यमान। इस मामले में, वॉल्यूम 50 एमपीसी क्यूब लें।
1000 Mpc के घन पक्ष के लिए, $\delta M/M \cong 10^{−4}$।
एकरूपता निर्धारित करने का एक तरीका सामूहिक उतार-चढ़ाव है। बड़े पैमाने पर उतार-चढ़ाव निचले पैमानों पर अधिक होगा।
आइसोट्रोपिक प्रकृति की मात्रा निर्धारित करने के लिए, कॉस्मिक माइक्रोवेव बैकग्राउंड रेडिएशन पर विचार करें। ब्रह्मांड बड़े कोणीय पैमाने पर लगभग आइसोट्रोपिक है।
याद दिलाने के संकेत
एक-दूसरे के पास से गुजरने वाली दो वस्तुओं में प्रकाश की गति से अधिक एक सापेक्ष वेग नहीं हो सकता है।
ब्रह्माण्ड संबंधी सिद्धांत बताता है कि ब्रह्मांड सजातीय और आइसोट्रोपिक है।
यह एकरूपता बहुत बड़े कोणीय पैमाने पर मौजूद है न कि छोटे पैमानों पर।
एसडीएसएस (स्लोअन डिजिटल स्काई सर्वे) कॉस्मोलॉजिकल सिद्धांत की पुष्टि करते हुए, रात के आकाश को मैप करने का एक प्रयास है।
ऊर्जा के संरक्षण और द्रव्यमान के संरक्षण के नियम के अनुसार, द्रव्यमान (E = mc 2 ) सहित ऊर्जा की कुल राशि ब्रह्मांड में किसी भी प्रक्रिया में हर चरण में अपरिवर्तित रहती है। ब्रह्मांड का विस्तार ऊर्जा की खपत करता है जो शायद फोटॉनों की तरंग दैर्ध्य (कॉस्मोलॉजिकल रेडशिफ्ट), डार्क एनर्जी इंटरैक्शन आदि से फैलती है।
26,000 से अधिक आकाशगंगाओं के सर्वेक्षण में तेजी लाने के लिए, Stephen A. Shectmanएक साथ 112 आकाशगंगाओं को मापने में सक्षम एक उपकरण बनाया गया। एक धातु की प्लेट में, आकाश में आकाशगंगाओं की स्थिति के अनुरूप छेद ड्रिल किए गए थे। फाइबर-ऑप्टिक केबल ने प्रत्येक आकाशगंगा से प्रकाश को 2.5 मीटर डु पोंट टेलीस्कोप में एक स्पेक्ट्रोग्राफ पर अलग चैनल पर नीचे ले जाया।Carnegie Observatories चिली में Cerro Las Campanas पर।
अधिकतम दक्षता के लिए, एक विशेष तकनीक जिसे के रूप में जाना जाता है Drift-Scan Photometryका उपयोग किया गया था, जिसमें एक सर्वेक्षण क्षेत्र की शुरुआत में दूरबीन को इंगित किया गया था और फिर स्वचालित ड्राइव को बंद कर दिया गया था। टेलिस्कोप अभी भी खड़ा था क्योंकि आकाश पिछले बहाव था। कंप्यूटर से जानकारी पढ़ेंCCD Detectorपृथ्वी के घूर्णन के समान दर पर, एक निरंतर आकाशीय अक्षांश पर एक लंबी, निरंतर छवि का निर्माण। फोटोमेट्री को पूरा करने में कुल 450 घंटे लगे।
शोर के विभिन्न रूप मौजूद हैं और उनके गुणों के आधार पर उनका गणितीय मॉडलिंग अलग है। विभिन्न भौतिक प्रक्रियाएं ब्रह्मांड के शक्ति स्पेक्ट्रम को बड़े पैमाने पर विकसित करती हैं। क्वांटम उतार-चढ़ाव के कारण लगाए गए प्रारंभिक बिजली स्पेक्ट्रम आवृत्ति की एक नकारात्मक तीसरी शक्ति का अनुसरण करते हैं जो कि इसका एक रूप हैPink Noise Spectrum तीन आयामों में।
मैट्रिक
ब्रह्मांड विज्ञान में, पहले अंतरिक्ष की एक परिभाषा होनी चाहिए। एक मीट्रिक एक गणितीय अभिव्यक्ति है जो अंतरिक्ष में बिंदुओं का वर्णन करता है। आकाश का अवलोकन एक गोलाकार ज्यामिति में किया जाता है; इसलिए एक गोलाकार समन्वय प्रणाली का उपयोग किया जाएगा। दो निकट दूरी वाले बिंदुओं के बीच की दूरी किसके द्वारा दी गई है -
$$ds^2 = dr^2 + r^2\theta ^2 + r^2 sin^2\theta d\phi^2$$
निम्न छवि 3-आयामी गैर-विस्तार वाले यूक्लिडियन स्थान में ज्यामिति दिखाती है।

यह ज्यामिति अभी भी 3-आयामी गैर-विस्तार वाले यूक्लिडियन स्थान में है। इसलिए, फ्रेम को परिभाषित करने वाली संदर्भ ग्रिड का विस्तार ही होगा। निम्न चित्र में बढ़ी हुई मीट्रिक को दर्शाया गया है।

एक स्केल फैक्टर को गैर-विस्तार वाले स्थान के समीकरण में डाल दिया जाता है, जिसे 'स्केल फैक्टर' कहा जाता है, जिसमें समय के साथ ब्रह्मांड का विस्तार शामिल होता है।
$$ds^2 = a^2(t)\left [ dr^2 + r^2\theta^2 + r^2 sin^2\theta d\phi^2 \right ]$$
कहाँ पे a(t) स्केल फैक्टर है, जिसे कभी-कभी लिखा जाता है R(t)। जहाँ तक,a(t) > 1 मेट्रिक का आवर्धन, जबकि a(t) < 1 का मतलब है मीट्रिक का सिकुड़ना और a(t) = 1लगातार मीट्रिक का मतलब है। एक सम्मेलन के रूप में,a(t0) = 1।
Comoving समन्वय प्रणाली
में Comoving Coordinate System, मापने का पैमाना फ्रेम (विस्तार ब्रह्मांड) के साथ फैलता है।
यहां ही $\left [ dr^2 + r^2\theta^2 + r^2 sin^2\theta d\phi^2 \right ]$ Comoving दूरी है, और $ds^2$ उचित दूरी है।
उचित दूरी अवलोकन के समय पृथ्वी से एक दूर की आकाशगंगा के मापा के रूप में वास्तविक दूरी के अनुरूप होगी, वस्तुओं की तात्कालिक दूरी उर्फ।
इसका कारण यह है कि एक फोटॉन द्वारा यात्रा की गई दूरी जब वह दूर के स्रोत से पर्यवेक्षक तक पहुंचती है, तो वह प्राप्त किया जाएगा $t=t_0$ पर्यवेक्षक, जिसका अर्थ होगा कि तात्कालिक रूप से देखी गई दूरी उचित दूरी होगी, और एक दर के कारक और संदर्भ के रूप में प्रारंभिक मापा लंबाई का उपयोग करके भविष्य की दूरी की भविष्यवाणी कर सकता है।
मनाया स्थान की दी गई मात्रा में आकाशगंगाओं की संख्या घनत्व के वास्तविक मूल्य को मापने के लिए कोमोविंग और उचित दूरी की अवधारणा महत्वपूर्ण है। जब मनाया फोटॉन उत्सर्जित होता है, तो उनके गठन के समय घनत्व की गणना करने के लिए कोमोविंग दूरी का उपयोग करना चाहिए। एक बार ब्रह्मांड के विस्तार की दर का अनुमान लगाया जा सकता है।
विस्तार की दर का अनुमान लगाने के लिए, एक लंबी अवधि में एक दूर की आकाशगंगा के अवलोकन में परिवर्तन का निरीक्षण किया जा सकता है।
याद दिलाने के संकेत
एक मीट्रिक एक गणितीय अभिव्यक्ति है जो अंतरिक्ष में बिंदुओं का वर्णन करता है।
स्केल फैक्टर यह निर्धारित करता है कि ब्रह्मांड अनुबंधित है या विस्तार कर रहा है।
एक कोमोडिंग समन्वय प्रणाली में, मापने का पैमाना फ्रेम (विस्तार ब्रह्मांड) के साथ फैलता है।
उचित दूरी वस्तुओं की तात्कालिक दूरी है।
कोमोविंग दूरी वस्तुओं की वास्तविक दूरी है।
इस अध्याय में, हम रॉबर्टसन-वॉकर मेट्रिक के बारे में विस्तार से समझेंगे।
समय के साथ स्केल फैक्टर बदलने के लिए मॉडल
मान लीजिए कि एक फोटॉन एक दूर की आकाशगंगा से उत्सर्जित होती है। अंतरिक्ष सभी दिशाओं में फोटॉन के लिए आगे है। ब्रह्मांड का विस्तार सभी दिशाओं में है। आइए देखें कि निम्न चरणों में समय के साथ स्केल फैक्टर कैसे बदलता है।
Step 1 - स्थिर ब्रह्माण्ड के लिए, स्केल फैक्टर 1 है, अर्थात कोमोविंग दूरी का मान पिंडों के बीच की दूरी है।
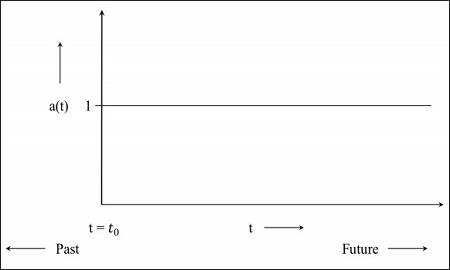
Step 2- निम्नलिखित छवि ब्रह्मांड का ग्राफ है जो अभी भी विस्तारित हो रहा है लेकिन कम दर पर, जिसका अर्थ है कि ग्राफ अतीत में शुरू होगा। t = 0 इंगित करता है कि ब्रह्मांड उस बिंदु से शुरू हुआ था।

Step 3 - निम्नलिखित छवि ब्रह्मांड के लिए ग्राफ है जो एक तेज दर से विस्तार कर रही है।

Step 4 - निम्नलिखित छवि ब्रह्मांड के लिए ग्राफ है जो अभी से अनुबंध करना शुरू करती है।

यदि स्केल फैक्टर का मान बन जाता है 0 ब्रह्मांड के संकुचन के दौरान, इसका तात्पर्य वस्तुओं के बीच की दूरी से है 0, यानी उचित दूरी बन जाती है 0। वर्तमान ब्रह्मांड में पिंडों के बीच की दूरी, एक निरंतर मात्रा है। भविष्य में, जब स्केल फैक्टर बन जाता है0, सब कुछ करीब आ जाएगा। मॉडल ब्रह्मांड के घटक पर निर्भर करता है।
फ्लैट के लिए मीट्रिक (यूक्लिडियन: वक्रता के लिए कोई पैरामीटर नहीं है) विस्तार ब्रह्मांड को निम्नानुसार दिया गया है -
$$ds^2 = a^2(t)\left ( dr^2+r^2d\theta^2+r^2sin^2\theta d\varphi^2 \right )$$
स्पेस-टाइम के लिए, उपरोक्त समीकरण में हमें प्राप्त लाइन तत्व को इस प्रकार संशोधित किया गया है -
$$ds^2 = c^2dt^2 - \left \{ a^2(t) \left ( dr^2 + r^2d\theta ^2 + r^2sin^2\theta d\varphi^2 \right ) \right \}$$
अंतरिक्ष के लिए - समय, जिस समय फोटॉन उत्सर्जित होता है और जब इसका पता लगाया जाता है तो वह अलग होता है। उचित दूरी उन वस्तुओं के लिए तात्कालिक दूरी है जो ब्रह्मांड के विस्तार के कारण समय के साथ बदल सकती हैं। यह वह दूरी है जो फोटॉन ने हमें प्राप्त करने के लिए विभिन्न वस्तुओं से यात्रा की थी। यह कोमोविंग दूरी से संबंधित है -
$$d_p = a(t) \times d_c$$
कहाँ पे $d_p$ उचित दूरी है और $d_c$ कोमोविंग दूरी है, जो तय हो गई है।
वर्तमान ब्रह्मांड में वस्तुओं के लिए मापी गई दूरी को कोमोविंग दूरी के रूप में लिया जाता है, जिसका अर्थ है कि कोमोविंग दूरी तय हो गई है और विस्तार से अपरिवर्तित है। अतीत के लिए, स्केल फैक्टर 1 से कम था, जो इंगित करता है कि उचित दूरी छोटा था।
हम एक आकाशगंगा में रेडशिफ्ट को माप सकते हैं। इसलिए उचित दूरी$d_p$ से मेल खाती है $c \times t(z)$, कहाँ पे $t(z)$एक redshift की ओर देखने का समय है और c निर्वात में प्रकाश की गति है। लुकबैक टाइम रेडशिफ्ट का एक फंक्शन है(z)।
उपरोक्त धारणा के आधार पर, हम विश्लेषण करते हैं कि इस परिदृश्य में ब्रह्माण्ड संबंधी लाल बदलाव की व्याख्या कैसे की जाती है $d_p = a(t) \times d_c$।
मान लें कि एक फोटॉन (जो पृथ्वी से बंधी है) को आकाशगंगा, जी। द्वारा उत्सर्जित किया जाता है $t_{em}$ उस समय से मेल खाती है जब फोटॉन उत्सर्जित होता था; $a(t_{em})$उस समय पैमाना कारक था जब फोटॉन उत्सर्जित होता था। फोटॉन का पता लगाने के समय तक, पूरे ब्रह्मांड का विस्तार हो गया था, अर्थात पहचान के समय फोटॉन को फिर से जोड़ा गया। $t_{obs}$ उस समय से मेल खाती है जब फोटॉन का पता लगाया जाता है और इसी पैमाने का कारक होता है $a(t_{obs})$।
ब्रह्माण्ड किसके द्वारा विकसित हुआ है वह कारक है -
$$\frac{a(t_{obs})}{a(t_{em})}$$
वह कारक जिसके द्वारा तरंगदैर्ध्य का विस्तार हुआ है -
$$\frac{\lambda_{obs}}{\lambda_{em}}$$
जो उस कारक के बराबर है जिसके द्वारा ब्रह्मांड विकसित हुआ है। प्रतीकों का अपना सामान्य अर्थ है। इसलिए,
$$\frac{a(t_{obs})}{a(t_{em})} = \frac{\lambda_{obs}}{\lambda_{em}}$$
हम उस कमी को जानते हैं (z) है -
$$z=\frac{\lambda_{obs} - \lambda_{em}}{\lambda_{em}} = \frac{\lambda_{obs}}{\lambda_{em}} - 1$$
$$1 + z = \frac{a(t_{obs})}{a(t_{em})}$$
स्केल फैक्टर का वर्तमान मूल्य 1 है, इसलिए $a(t_{obs}) = 1$ और जब फोटॉन द्वारा अतीत में उत्सर्जित किया गया था, तो स्केल कारक को दर्शाते हुए $a(t)$।
इसलिए,
$$1 + z = \frac{1}{a(t)}$$
कॉस्मोलॉजी में रेडशिफ्ट की व्याख्या
इसे समझने के लिए, हम निम्नलिखित उदाहरण लेते हैं: यदि $z = 2$ फिर $a(t) = 1/3$।
इसका तात्पर्य यह है कि ब्रह्मांड का विस्तार तीन के एक कारक से हुआ है क्योंकि प्रकाश ने उस वस्तु को छोड़ दिया है। प्राप्त विकिरण की तरंग दैर्ध्य का विस्तार तीन के एक कारक से हुआ है क्योंकि उत्सर्जन वस्तु से उसके पारगमन के दौरान एक ही कारक द्वारा अंतरिक्ष का विस्तार हुआ है। यह ध्यान दिया जाना चाहिए कि इतने बड़े मूल्यों परz, रेडशिफ्ट मुख्य रूप से कॉस्मोलॉजिकल रेडशिफ्ट है, और यह हमारे संबंध में वस्तु के वास्तविक पुनरावर्तन वेग का एक वैध उपाय नहीं है।
कॉस्मिक माइक्रोवेव बैकग्राउंड के लिए (CMB), z = 1089, जिसका अर्थ है कि वर्तमान ब्रह्मांड का विस्तार कारक के रूप में हुआ है ∼1090। फ्लैट, यूक्लिडियन, विस्तारित ब्रह्मांड के लिए मीट्रिक इस प्रकार है -
$$ds^2 = a^2(t)(dr^2 + r^2d\theta^2 + r^2sin^2\theta d\varphi^2)$$
हम किसी भी वक्रता में मीट्रिक लिखना चाहते हैं।
Robertson and Walker किसी भी वक्रता ब्रह्माण्ड (जो सजातीय और आइसोट्रोपिक है) के लिए सिद्ध होता है, मेट्रिक इस प्रकार दिया जाता है -
$$ds^2 = a^2(t) \left [ \frac{dr^2}{1-kr^2} + r^2d\theta^2 + r^2sin^2\theta d\varphi^2 \right ]$$
यह आमतौर पर के रूप में जाना जाता है Robertson–Walker Metricऔर अंतरिक्ष के किसी भी टोपोलॉजी के लिए सच है। कृपया अतिरिक्त कारक पर ध्यान दें$dr^2$। यहाँ वक्रता स्थिर है।
ब्रह्मांड की ज्यामिति
ब्रह्माण्ड की ज्यामिति को निम्नलिखित वक्रताओं की सहायता से समझाया गया है, जिसमें शामिल हैं -
- सकारात्मक वक्रता
- नकारात्मक वक्रता
- शून्य वक्रता
आइए हम इनमें से प्रत्येक को विस्तार से समझें।
सकारात्मक वक्रता
यदि वक्रता की सतह पर किसी बिंदु पर खींची गई स्पर्शरेखा तल सतह पर किसी बिंदु पर प्रतिच्छेद नहीं करता है, तो इसे धनात्मक वक्रता वाली सतह कहा जाता है अर्थात सतह उस बिंदु पर स्पर्शरेखा तल के एक तरफ रहती है। क्षेत्र की सतह में सकारात्मक वक्रता है।
नकारात्मक वक्रता
यदि वक्रता की सतह पर एक बिंदु पर खींची गई एक स्पर्शरेखा तल सतह पर किसी बिंदु पर स्थित है, तो इसे एक नकारात्मक वक्रता वाली सतह कहा जाता है, अर्थात सतह दो अलग-अलग दिशाओं में स्पर्शरेखा तल से दूर घटती है। एक काठी के आकार की सतह पर एक नकारात्मक वक्रता होती है।
अब एक गोले की सतह पर विचार करें। यदि त्रिभुज की सतह पर त्रिभुज का निर्माण जियोडेसिक (महान वृत्तों के चाप) के साथ तीन बिंदुओं के साथ किया जाता है, तो गोलाकार त्रिभुज के आंतरिक कोणों का योग 180 o से अधिक होता है , अर्थात -
$$\alpha + \beta + \gamma > \pi$$
ऐसे स्थानों को सकारात्मक रूप से घुमावदार स्थान कहा जाता है। इसके अलावा, वक्रता समरूप और समस्थानिक है। सामान्य तौर पर, गोलाकार त्रिभुज के कोण पर संबंध निम्नानुसार है -
$$\alpha + \beta +\gamma = \pi + A/R^2$$
कहाँ पे A त्रिभुज का क्षेत्रफल और है Rक्षेत्र की त्रिज्या है। निम्न छवि एक सकारात्मक घुमावदार स्थान को दर्शाती है।

सकारात्मक वक्रता के लिए, समानांतर रेखाओं को मिलना चाहिए। पृथ्वी की सतह पर विचार करें, जो एक सकारात्मक रूप से घुमावदार स्थान है। भूमध्य रेखा पर दो शुरुआती बिंदु लें। वे रेखाएँ जो समकोण पर समकोण को पार करती हैं, देशांतर रेखाओं के रूप में जानी जाती हैं। चूंकि ये रेखाएं समकोण पर समकोण से पार करती हैं, इसलिए उन्हें समानांतर रेखाओं के रूप में संदर्भित किया जा सकता है। भूमध्य रेखा से शुरू होकर, वे अंततः ध्रुवों पर प्रतिच्छेद करते हैं। इस विधि का उपयोग किया गया थाCarl Gauss और दूसरों को पृथ्वी की टोपोलॉजी को समझने के लिए।
एक नकारात्मक रूप से घुमावदार जगह पर विचार करें (निम्नलिखित छवि में दिखाया गया एक काठी), त्रिकोण के आंतरिक कोणों का योग 180 ओ से कम है , अर्थात -
$$\alpha + \beta + \gamma < \pi$$
कोण पर कोण संबंध का अनुसरण करता है -
$$\alpha + \beta + \gamma = \pi - A/R^2$$

शून्य वक्रता
एक विमान की सतह में शून्य वक्रता होती है। अब एक सपाट स्थान के लिए, यदि एक विमान लिया जाता है और एक त्रिभुज का निर्माण भू-स्थान (सीधी रेखाओं) के साथ तीन बिंदुओं को जोड़कर किया जाता है, तो कोणों का आंतरिक योग होगा -
$$\alpha + \beta + \gamma = \pi$$
निम्न छवि समतल 2-आयामी स्थान है।

यदि कोई समरूप और समस्थानिक होना चाहता है, तो केवल तीन संभावनाएँ रह जाती हैं: अंतरिक्ष समान रूप से सपाट हो सकता है या इसमें एक समान सकारात्मक वक्रता हो सकती है या इसमें एक समान नकारात्मक वक्रता हो सकती है।
वक्रता स्थिरांक निम्न तीन मानों में से किसी को भी मान सकता है।
$$k = \begin{cases}+1, & for \: a\: positively \: curved\: space;\\\quad 0, & for\: a \: flat \: space;\\-1, & for\: a \: negatively \: curved \: space;\end{cases}$$
ब्रह्मांड की वैश्विक टोपोलॉजी
ब्रह्मांड की एक निश्चित टोपोलॉजी है, लेकिन स्थानीय रूप से इसमें झुर्रियां हो सकती हैं। अंतरिक्ष में पदार्थ कैसे वितरित किया जाता है, इसके आधार पर, वक्रता में छोटे बदलाव होते हैं। आइए हम मान लें कि वस्तुओं का एक वर्ग है जिसका समान आकार है कोई फर्क नहीं पड़ता कि यह ब्रह्मांड में कहां है, जिसका अर्थ है कि वे मोमबत्ती की तरह हैं। उनके पास समान चमक नहीं है, लेकिन उनका आकार समान है।
यदि वस्तु सकारात्मक रूप से घुमावदार स्थान पर है और फोटॉनों बिंदु ए (वस्तु का एक छोर) और बी (वस्तु का दूसरा छोर) से आता है, तो फोटॉनों जियोडेसिक के मार्ग के माध्यम से सकारात्मक रूप से घुमावदार स्थान में समानांतर प्रचार करेंगे और वे अंततः मिलेंगे। । सी में एक पर्यवेक्षक के लिए, ऐसा लगेगा कि यह दो अलग-अलग बिंदुओं से अलग-अलग दिशाओं में आया था।
यदि वस्तु स्थानीय ब्रह्मांड में है और हम कोणीय आकार को मापते हैं, तो यह वक्रता से प्रभावित नहीं होता है। यदि समान श्रेणी के ऑब्जेक्ट को अधिक से अधिक रेडशिफ्ट पर देखा जाता है, तो कोणीय आकार के साथ संबंध नहीं होता है।
$$\theta = \frac{d}{r}$$
कहाँ पे d वस्तु का आकार है और rवस्तु की दूरी है, अर्थात यदि आकार स्थानीय आकार से अधिक है, तो इसका मतलब है कि वक्रता सकारात्मक है। निम्नलिखित छवि एक सकारात्मक रूप से घुमावदार स्थान में पता लगाए गए फोटॉन का प्रतिनिधित्व है।

यह ध्यान दिया जाना चाहिए कि कोई वास्तविक ज्योतिषीय वस्तु नहीं है जो मानक आकार और आकृति विज्ञान की है। हालांकि एक विशाल अण्डाकार cD - आकाशगंगाओं को मानक मोमबत्तियों को फिट करने के लिए सोचा गया था, लेकिन वे भी समय के साथ विकसित होते पाए गए।
आकाशगंगाओं के दूरियों का पता लगाना
इस खंड में, हम चर्चा करेंगे कि निम्नलिखित छवि को ध्यान में रखकर एक आकाशगंगा की दूरी कैसे ज्ञात करें।

एक कॉस्मोलॉजिकल रेस्ट फ्रेम में मिल्की वे (आर, θ) पर विचार करें। एक ले सकता है = 0; (0, of, ϕ), यानी समरूपता की धारणा को लागू करके ब्रह्मांड का केंद्र।
एक आकाशगंगा 'जी' पर (आर 1,),) पर विचार करें। दूरी (उचित) एक फोटॉन द्वारा यात्रा की गई सबसे छोटी रेडियल दूरी है। अंतरिक्ष की समरूपता से - समय, n = 0 से r = r1 तक की अशक्त भू-आकृति, अंतरिक्ष में एक स्थिर दिशा है। इसके रेडियल प्रसार में, कोणीय निर्देशांक नहीं बदलते हैं। यदि कोणीय निर्देशांक परिवर्तित हो जाते हैं, तो यह सबसे छोटा मार्ग नहीं है। यही कारण है कि कर्व अवधि 2 डीआर में मौजूद है ।
याद दिलाने के संकेत
ब्रह्मांड का विस्तार सभी दिशाओं में है।
पैमाने कारक विकास के आधार पर ब्रह्मांड स्थिर, विस्तार या अनुबंधित हो सकता है।
CD-galaxies समय के साथ विकसित होती है और इसलिए इसे मानक मोमबत्तियों के रूप में इस्तेमाल नहीं किया जा सकता है।
ब्रह्मांड में कुछ टोपोलॉजी है, लेकिन स्थानीय रूप से इसमें झुर्रियां हो सकती हैं।
इस अध्याय में, हम हबल पैरामीटर के साथ-साथ स्केल फैक्टर के बारे में चर्चा करेंगे।
Prerequisite - कॉस्मोलॉजिकल रेडशिफ्ट, कॉस्मोलॉजिकल प्रिंसिपल्स।
Assumption - ब्रह्मांड समरूप और आइसोट्रोपिक है।
स्केल फैक्टर के परिवर्तन की दर के साथ हबल की निरंतरता
इस खंड में, हम हबल के कॉन्स्टेंट को स्केल ऑफ़ फैक्टर की आंशिक दर के साथ संबंधित करेंगे।
हम निम्नलिखित तरीके से वेग लिख सकते हैं और सरल कर सकते हैं।
$$v = \frac{\mathrm{d} r_p}{\mathrm{d} t}$$
$$= \frac{d[a(t)r_c}{dt}$$
$$v = \frac{\mathrm{d} a}{\mathrm{d} t} \ast \frac{1}{a} \ast (ar_c)$$
$$v = \frac{\mathrm{d} a}{\mathrm{d} t} \ast \frac{1}{a} \ast r_p$$
यहाँ, v पुनरावर्तन वेग है, a पैमाना कारक है और rp आकाशगंगाओं के बीच उचित दूरी है।
Hubble’s Empirical Formula प्रकृति का था -
$$v = H \ast r_p$$
इस प्रकार, उपर्युक्त दो समीकरणों की तुलना -
Hubble’s Parameter = Fractional rate of change of the scale factor
$$H = da/dt \ast 1/a$$
Note- यह एक स्थिर नहीं है क्योंकि स्केल फैक्टर समय का एक फ़ंक्शन है। इसलिए इसे हबल का पैरामीटर कहा जाता है, न कि हबल के स्थिरांक को।
अनुभवपूर्वक हम लिखते हैं -
$$H = V/D$$
इस प्रकार, इस समीकरण से, हम यह अनुमान लगा सकते हैं कि कब से D बढ़ रहा है और V एक स्थिर है, तो H ब्रह्मांड के समय और विस्तार के साथ कम हो जाता है।
फ्राइडमैन समीकरण रॉबर्टसन-वॉकर मॉडल के साथ संयोजन के रूप में
इस खंड में, हम समझेंगे कि रॉबर्टसन-वॉकर मॉडल के साथ संयोजन में फ्राइडमैन समीकरण का उपयोग कैसे किया जाता है। इसे समझने के लिए, हम निम्नलिखित छवि लेते हैं, जिसमें दूरी पर एक परीक्षण द्रव्यमान होता हैrp द्रव्यमान के शरीर से M उदाहरण के तौर पे।

उपरोक्त छवि को ध्यान में रखते हुए, हम बल को व्यक्त कर सकते हैं -
$$F = G \ast M \ast \frac{m}{r^2_p}$$
यहाँ, G सार्वभौमिक गुरुत्वाकर्षण स्थिरांक है और ρ अवलोकन ब्रह्मांड के अंदर पदार्थ घनत्व है।
अब, क्षेत्र के भीतर एक समान द्रव्यमान घनत्व को हम लिख सकते हैं -
$$M = \frac{4}{3} \ast \pi \ast r_p^3 \ast \rho$$
अपने बल समीकरण में इनका उपयोग करके हम प्राप्त करते हैं -
$$F = \frac{4}{3} \ast \pi \ast G \ast r_p \ast \rho \ast m$$
इस प्रकार, हम द्रव्यमान की संभावित ऊर्जा और गतिज ऊर्जा लिख सकते हैं m के रूप में -
$$V = -\frac{4}{3} \ast \pi \ast G \ast r^2_p \ast m \ast \rho$$
$$K.E = \frac{1}{2} \ast m \ast \frac{\mathrm{d} r_p^2}{\mathrm{d} t}$$
का उपयोग करते हुए Virial Theorem -
$$U = K.E + V$$
$$U = \frac{1}{2} \ast m \ast \left ( \frac{\mathrm{d} r_p}{\mathrm{d} t} \right )^2 - \frac{4}{3} \ast \pi \ast G \ast r_p^2 \ast m \ast \rho$$
लेकिन यहाँ, $r_p = ar_c$। तो, हम -
$$U = \frac{1}{2} \ast m \ast \left ( \frac{\mathrm{d} a}{\mathrm{d} t} \right )^2 r_c^2 - \frac{4}{3} \ast \pi \ast G \ast r_p^2 \ast m \ast \rho$$
आगे सरलीकरण पर, हम फ्रीडमैन समीकरण प्राप्त करते हैं,
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi}{3} \ast G \ast \rho + \frac{2U}{m} \ast r_c^2 \ast a^2$$
यहाँ Uएक स्थिर है। हम यह भी ध्यान देते हैं कि वर्तमान में हम जिस ब्रह्मांड में रहते हैं, उस पर पदार्थ का प्रभुत्व है, जबकि विकिरण ऊर्जा का घनत्व बहुत कम है।
याद दिलाने के संकेत
हबल पैरामीटर ब्रह्मांड के समय और विस्तार के साथ कम हो जाता है।
वर्तमान में हम जिस ब्रह्मांड में रहते हैं उस पर पदार्थ का प्रभुत्व है और विकिरण ऊर्जा का घनत्व बहुत कम है।
इस अध्याय में, हम समझेंगे कि फ्रीडमैन समीकरण क्या है और विभिन्न वक्रता स्थिरांक के लिए विश्व मॉडल के बारे में विस्तार से अध्ययन करें।
फ्रीडमैन समीकरण
यह समीकरण हमें ब्रह्मांड के सजातीय और आइसोट्रोपिक मॉडल में अंतरिक्ष के विस्तार के बारे में बताता है।
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho + \frac{2U}{mr_c^2a^2}$$
के संदर्भ में इसे संशोधित किया गया था General Relativity (जीआर) और रॉबर्टसन-वॉकर मीट्रिक निम्नानुसार है।
जीआर समीकरणों का उपयोग करना -
$$\frac{2U}{mr_c^2} = -kc^2$$
कहाँ पे kवक्रता स्थिर है। इसलिए,
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8 \pi G}{3}\rho - \frac{kc^2}{a^2}$$
इसके अलावा, $\rho$ऊर्जा घनत्व द्वारा प्रतिस्थापित किया जाता है जिसमें पदार्थ, विकिरण और ऊर्जा का कोई अन्य रूप शामिल होता है। लेकिन अभिप्रेरक उद्देश्यों के लिए, इसे लिखा जाता है$\rho$।
विभिन्न वक्रता स्थिरांक के लिए विश्व मॉडल
आइए अब वक्रता स्थिर मूल्यों के आधार पर विभिन्न संभावनाओं को देखें।
केस 1: k = 1, या बंद ब्रह्मांड
एक विस्तारित ब्रह्मांड के लिए, $da/dt > 0$। जैसा कि विस्तार जारी है, उपरोक्त समीकरण के आरएचएस पर पहला शब्द इस प्रकार है$a^{-3}$, जबकि दूसरा शब्द के रूप में जाता है $a^{-2}$। जब दो शब्द समान हो जाते हैं तो ब्रह्मांड का विस्तार रुक जाता है। फिर -
$$\frac{8 \pi G}{3}\rho = \frac{kc^2}{a^2}$$
यहाँ, k = 1, इसलिए,
$$a = \left [ \frac{3c^2}{8 \pi G\rho} \right ]^{\frac{1}{2}}$$
ऐसा ब्रह्मांड परिमित है और परिमित मात्रा है। इसे क्लोज्ड यूनिवर्स कहा जाता है।
केस 2: k = -1, या ओपन यूनिवर्स
अगर k < 0विस्तार कभी नहीं रुकेगा। कुछ बिंदु के बाद, दूसरे कार्यकाल की तुलना में आरएचएस पर पहले शब्द की उपेक्षा की जा सकती है।
यहाँ, के = -1। इसलिए,$da/dt ∼ c$।
इस मामले में, ब्रह्मांड तटीय है। ऐसे ब्रह्मांड में अनंत स्थान और समय है। इसे ओपन यूनिवर्स कहा जाता है।
केस 3: के = 0, या फ्लैट यूनिवर्स
इस मामले में, ब्रह्मांड कम दर पर विस्तार कर रहा है। यहाँ, k = 0. इसलिए,
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho$$
ऐसे ब्रह्मांड में अनंत स्थान और समय है। इसे फ्लैट यूनिवर्स कहा जाता है।
याद दिलाने के संकेत
फ्राइडमैन समीकरण हमें ब्रह्मांड के समरूप और समधर्मी मॉडल में अंतरिक्ष के विस्तार के बारे में बताता है।
विभिन्न वक्रता निरंतर मूल्यों के आधार पर, हमारे पास एक बंद, खुला या सपाट ब्रह्मांड हो सकता है।
इस अध्याय में, हम द्रव समीकरण पर चर्चा करेंगे और यह हमें ब्रह्मांड के घनत्व के बारे में बताता है जो समय के साथ बदलता है।
वर्तमान ब्रह्मांड में ρ c और ρ का अनुमान लगाना
वर्तमान ब्रह्मांड के लिए -
$$\rho_c \simeq 10^{11}M_\odot M_{pc}^{-3} \simeq 10\: hydrogen \: atoms \: m^{-3}$$
हमारे बाहरी अंतरिक्ष में महत्वपूर्ण घनत्व की एक पूरी श्रृंखला है। जैसे, अंतरजाल माध्यम के लिए$\rho_c$ 1 हाइड्रोजन परमाणु है $m^{-3}$, जबकि आणविक बादलों के लिए यह है $10^6$ हाइड्रोजन परमाणु $m^{−3}$।
हमें मापना चाहिए $\rho_c$अंतरिक्ष के उचित नमूनों पर विचार करना। हमारी आकाशगंगा के भीतर, का मूल्य$\rho_c$बहुत अधिक है, लेकिन हमारी आकाशगंगा पूरे ब्रह्मांड का प्रतिनिधि नहीं है। इसलिए, हमें अंतरिक्ष में जाना चाहिए जहां ब्रह्मांडीय सिद्धांत धारण करता है, अर्थात, दूरी should 300 Mpc। 300 Mpc को देखने का मतलब है कि 1 बिलियन वर्ष पीछे देखना, लेकिन यह अभी भी वर्तमान ब्रह्मांड है।
एसडीएसएस जैसे सर्वेक्षण वास्तविक मामले के घनत्व को निर्धारित करने के लिए आयोजित किए जाते हैं। वे 5 × 500 × 5 Mpc 3 मात्रा लेते हैं , आकाशगंगाओं की संख्या की गणना करते हैं और इन आकाशगंगाओं से आने वाले सभी प्रकाश को जोड़ते हैं। एक धारणा के तहत कि 1 एल M 1 एम, यानी 1 सौर ल्यूमिनोसिटी Mass 1 सौर द्रव्यमान।
हम एक बड़े पैमाने पर रूपांतरण के लिए एक प्रकाश करते हैं और फिर हम उस मात्रा में मौजूद दृश्यमान कणों के आधार पर बैरियों की संख्या का अनुमान लगाने की कोशिश करते हैं।
उदाहरण के लिए,
$$1000L_\odot ≡ 1000M_\odot / m_p$$
जहां, एम पी = प्रोटॉन का द्रव्यमान।
तब हमें मोटे तौर पर बेरोन संख्या घनत्व मिलता है $\Omega b ∼= 0.025$। इसका अर्थ है$\rho b = 0.25%$ का $\rho_c$। अलग-अलग सर्वेक्षणों से थोड़ा अलग मूल्य मिला है। इसलिए, स्थानीय ब्रह्मांड में, दृश्यमान पदार्थ की संख्या घनत्व महत्वपूर्ण घनत्व से बहुत कम है, जिसका अर्थ है कि हम एक खुले ब्रह्मांड में रह रहे हैं।
10 के कारक वाले द्रव्यमान को इन सर्वेक्षणों में शामिल नहीं किया जाता है क्योंकि ये सर्वेक्षण विद्युत चुम्बकीय विकिरण के लिए होते हैं लेकिन अंधेरे पदार्थ नहीं। , दे$\Omega_m = 0.3 − 0.4$। फिर भी निष्कर्ष निकाला कि हम एक खुले ब्रह्मांड में रह रहे हैं।
डार्क मैटर ग्रेविटी से इंटरैक्ट करता है। बहुत सारे काले पदार्थ विस्तार को रोक सकते हैं। हमने अभी तक औपचारिकता नहीं की है कि कैसे$\rho$ समय के साथ परिवर्तन, जिसके लिए हमें समीकरणों के एक और सेट की आवश्यकता है।
ऊष्मागतिकी में कहा गया है कि -
$$dQ = dU + dW$$
आकार के संदर्भ में बढ़ती प्रणाली के लिए, $dW = P dV$। ब्रह्मांड का विस्तार एडियाबेटिक यानी मॉडलिंग के रूप में किया जाता है$dQ = 0$। इसलिए, वॉल्यूम परिवर्तन आंतरिक ऊर्जा dU में परिवर्तन से होना चाहिए।
आइए हम ब्रह्मांड के कुछ निश्चित भाग कोमोडिंग त्रिज्या की श्रेणी में आते हैं $r_c = 1$। अगर$\rho$ अंतरिक्ष की इस मात्रा के भीतर सामग्री का घनत्व क्या है,
$$M = \frac{4}{3} \pi a^3r_c^3 \rho$$
$$U = \frac{4}{3}\pi a^3\rho c^2$$
कहाँ पे, Uऊर्जा घनत्व है। आइए हम समय के साथ आंतरिक ऊर्जा में परिवर्तन का पता लगाएं क्योंकि ब्रह्मांड का विस्तार हो रहा है।
$$\frac{\mathrm{d} U}{\mathrm{d} t} = 4 \pi a^2 \rho c^2 \frac{\mathrm{d} a}{\mathrm{d} t} + \frac{4}{3}\pi a^3 c^2\frac{\mathrm{d} \rho}{\mathrm{d} t}$$
इसी तरह, समय के साथ मात्रा में परिवर्तन के द्वारा दिया जाता है,
$$\frac{\mathrm{d} V}{\mathrm{d} t} = 4\pi a^2 \frac{\mathrm{d} a}{\mathrm{d} t}$$
स्थानापन्न $dU = −P dV$। हमें मिला,
$$4\pi a^2(c^2 \rho +P)\dot{a}+\frac{4}{3}\pi a^3c^2\dot{\rho} = 0$$
$$\dot{\rho}+3\frac{\dot{a}}{a}\left ( \rho + \frac{P}{c^2} \right ) = 0$$
इसे कहते हैं Fluid Equation। यह हमें बताता है कि समय के साथ ब्रह्मांड का घनत्व कैसे बदलता है।
ब्रह्मांड के फैलते ही दबाव कम हो जाता है। हर पल दबाव बदल रहा है, लेकिन माना मात्रा में दो बिंदुओं के बीच कोई दबाव अंतर नहीं है, इसलिए, दबाव ढाल शून्य है। केवल सापेक्षतावादी सामग्री दबाव प्रदान करती है, पदार्थ दबाव कम होता है।
फ्राइडमैन समीकरण द्रव समीकरण ब्रह्मांड के साथ।
याद दिलाने के संकेत
डार्क मैटर ग्रेविटी से इंटरैक्ट करता है। बहुत सारे काले पदार्थ विस्तार को रोक सकते हैं।
द्रव समीकरण हमें बताता है कि समय के साथ ब्रह्मांड का घनत्व कैसे बदलता है।
फ्राइडमैन समीकरण द्रव समीकरण ब्रह्मांड के साथ।
केवल सापेक्षतावादी सामग्री दबाव प्रदान करती है, पदार्थ दबाव कम होता है।
इस अध्याय में, हम मैटर डॉमिनेटेड यूनिवर्स से संबंधित फ्रीडमैन समीकरणों के समाधान पर चर्चा करेंगे। ब्रह्मांड विज्ञान में, क्योंकि हम सब कुछ बड़े पैमाने पर देख रहे हैं, सौर मंडल, आकाशगंगाएं, सब कुछ धूल के कणों की तरह होता है (यही हम इसे अपनी आंखों से देखते हैं), हम इसे धूल भरा ब्रह्मांड या केवल ब्रह्मांड कह सकते हैं।
में Fluid Equation,
$$\dot{\rho} = -3\left ( \frac{\dot{a}}{a} \right )\rho -3\left ( \frac{\dot{a}}{a} \right )\left ( \frac{P}{c^2} \right )$$
हम देख सकते हैं कि एक दबाव अवधि है। धूल भरे ब्रह्मांड के लिए,P = 0, क्योंकि पदार्थ का ऊर्जा घनत्व विकिरण के दबाव से अधिक होगा, और मामला सापेक्ष गति से नहीं बढ़ रहा है।
तो, द्रव समीकरण बन जाएगा,
$$\dot{\rho} = -3\left ( \frac{\dot{a}}{a} \right )\rho$$
$$\Rightarrow \dot{\rho}a + 3\dot{a}\rho = 0$$
$$\Rightarrow \frac{1}{a^3}\frac{\mathrm{d}}{\mathrm{d} t}(a^3 \rho) = 0$$
$$\Rightarrow \rho a^3 =\: constant$$
$$\Rightarrow \rho \propto \frac{1}{a^3}$$
इस समीकरण में कोई काउंटर अंतर्ज्ञान नहीं है क्योंकि घनत्व को पैमाने पर होना चाहिए $a^{-3}$ क्योंकि वॉल्यूम बढ़ रहा है $a^3$।
पिछले संबंध से, हम कह सकते हैं कि,
$$\frac{\rho (t)}{\rho_0} = \left [ \frac{a_0}{a(t)} \right ]^3$$
वर्तमान ब्रह्मांड के लिए, a, जो बराबर है a0 होना चाहिए 1. तो,
$$\rho(t) = \frac{\rho_0}{a^3}$$
समतल ब्रह्मांड में एक मामले में, k = 0. तो, फ्रीडमैन समीकरण बन जाएगा,
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8 \pi G\rho}{3}$$
$$\dot{a}^2 = \frac{8\pi G \rho a^2}{3}$$
इस समीकरण को हल करके, हम प्राप्त करेंगे,
$$a \propto t^{2/3}$$
$$\frac{a(t)}{a_0} = \left ( \frac{t}{t_0} \right )^{2/3}$$
$$a(t) = \left( \frac{t}{t_0} \right )^{2/3}$$
इसका मतलब यह है कि ब्रह्मांड घटती दर के साथ बढ़ता रहेगा। निम्नलिखित छवि डस्टी यूनिवर्स के विस्तार को दर्शाती है।

Ρ समय के साथ कैसे बदलता है?
निम्नलिखित समीकरण पर एक नज़र डालें -
$$\frac{\rho(t)}{\rho_0} = \left ( \frac{t_0}{t} \right )^2$$
हम जानते हैं कि स्केल फैक्टर समय के साथ बदलता रहता है $t^{2/3}$। इसलिए,
$$a(t) = \left ( \frac{t}{t_0} \right )^{2/3}$$
इसे अलग करते हुए, हम प्राप्त करेंगे,
$$\frac{(da)}{dt} = \dot{a} = \frac{2}{3} \left ( \frac{t^{-1/3}}{t_0} \right )$$
हम जानते हैं कि Hubble Constant है,
$$H(t) = \frac{\dot{a}}{a} = \frac{2}{3t}$$
इसके लिए समीकरण है Einstein-de sitter Universe। यदि हम ब्रह्मांड की वर्तमान आयु की गणना करना चाहते हैं,
$$t_0 = t_{age} = \frac{2}{3H_0}$$
का मान रखने के बाद $H_0$ वर्तमान ब्रह्मांड के लिए, हमें ब्रह्मांड की आयु का मान मिलेगा 9 Gyrs। वहां कई हैंGlobular Cluster हमारे अपने दूधिया तरीके की आकाशगंगा में जो कि उम्र से अधिक है।
वह सब धूल भरे ब्रह्मांड के बारे में था। अब, यदि आप मानते हैं कि ब्रह्मांड में विकिरण का प्रभुत्व है और पदार्थ से नहीं, तो विकिरण ऊर्जा घनत्व के रूप में चला जाता है$a^{-4}$ बजाय $a^{-3}$। हम इसे अगले अध्याय में देखेंगे।
याद दिलाने के संकेत
ब्रह्मांड विज्ञान में, सब कुछ धूल के कणों की तरह होता है, इसलिए, हम इसे धूल भरा ब्रह्मांड या केवल ब्रह्मांड कहते हैं।
अगर हम यह मान लें कि ब्रह्मांड में विकिरण का प्रभुत्व है और पदार्थ से नहीं, तो विकिरण ऊर्जा घनत्व के रूप में चला जाता है $a^{-4}$ बजाय $a^{-3}$।
इस अध्याय में, हम रेडिएशन डोमिनेटेड यूनिवर्स से संबंधित फ्रीडमैन समीकरणों के समाधानों पर चर्चा करेंगे। शुरुआत में, हम विकिरण के मामले में ऊर्जा घनत्व की तुलना करते हैं। यह हमें यह देखने में सक्षम करेगा कि क्या हमारे ब्रह्मांड का प्रभुत्व है या विकिरण का प्रभुत्व है।
विकिरण का ऊर्जा घनत्व
वर्तमान ब्रह्मांड में प्रचलित विकिरण को तारकीय स्रोतों के लिए बहुत कम जिम्मेदार ठहराया जा सकता है, लेकिन इसका मुख्य कारण अवशेष सीएमबी (कॉस्मिक माइक्रोवेव बैकग्राउंड) है।
विकिरण की ऊर्जा घनत्व, $\epsilon_{\gamma,0}$, निम्नानुसार व्यक्त किया जा सकता है -
$$\epsilon_{\gamma,0} = aT_0^4$$
यहाँ, a विकिरण स्थिरांक है जिसकी अभिव्यक्ति है $(8\pi^5k_B^4)/(15h^3c^2)$ के बराबर a = 7.5657 × 10−15erg\: cm−3 K−4। तापमान, T0, हम यहाँ पर विचार करते हैं, जो CMB के अनुरूप काले शरीर से मेल खाता है।
परिणामों को प्रतिस्थापित करते हुए, हमारे पास,
$$\epsilon_{\gamma,0} = aT_0^4 = 4 \times 10^{-13}erg\: cm^{-3}$$
पदार्थ का ऊर्जा घनत्व
निम्नलिखित गणनाओं में, हमारे पास एक सपाट ब्रह्मांड और के = 0. के साथ काम करने की धारणा है। हम पदार्थ की ऊर्जा घनत्व के रूप में मानते हैं $\epsilon = \rho c^2$। हम निम्नलिखित पर विचार करते हैं -
$$\rho_{m,0}c^2 = 0.3\rho_{c,0}c^2 = 0.3 \times \frac{3H_0^2}{8\pi G} \times c^2$$
$$\rho_{m,0}c^2 \simeq 2 \times 10^{-8} erg \:cm^{-3}$$
$$\rho_{b,0}c^2 = 0.03\rho_{c,0}c^2 = 0.03 \times \frac{3H_0^2}{8\pi G} \times c^2$$
$$\rho_{b,0}c^2 \simeq 2 \times 10^{-9} erg\: cm^{-3}$$
इस प्रकार, उपरोक्त गणना से, हम देखते हैं कि हम एक पदार्थ-प्रभुत्व वाले ब्रह्मांड में रहते हैं। यह इस तथ्य से समर्थित हो सकता है कि सीएमबी बहुत ठंडा है। जैसा कि हम समय में पीछे देखते हैं, हमारे पास सीएमबी तापमान अधिक गर्म होता जा रहा है, और यह निष्कर्ष निकालने में सक्षम होगा कि एक युग हो सकता है जहां ब्रह्मांड विकिरण का प्रभुत्व था।
घनत्व और स्केल फैक्टर का परिवर्तन
द्रव समीकरण हमें दिखाता है कि -
$$\dot{\rho} + 3\frac{\dot{a}}{a}\left ( \rho + \frac{P}{c^2} \right ) = 0$$
यदि हम एक धूल भरे ब्रह्मांड पर विचार करते हैं, तो हमारे पास P = 0. पिछले परिणामों को अलग करते हुए, हम ब्रह्मांड को विकिरण के प्रभुत्व के रूप में मानते हैं।
$$\dot{\rho}_{rad} + 3 \frac{\dot{a}}{a}\left ( \rho_{rad} + \frac{P}{c^2} \right ) = 0$$
के दबाव संबंध का उपयोग करना $P_{rad} = \rho c^{2/3}$ हमारे पास है -
$$\dot{\rho}_{rad} + 3 \frac{\dot{a}}{a}\left ( \rho_{rad} + \frac{\rho_{rad}}{3} \right ) = 0$$
$$\dot{\rho}_{rad} + 4\frac{\dot{a}}{a}(\rho_{rad}) = 0$$
आगे सरलीकरण पर, हमारे पास,
$$\frac{1}{a^4}\frac{\mathrm{d}}{\mathrm{d} t}(\rho_{rad}a^4) = 0$$
$$\rho_{rad}a^4 =\: constant$$
$$\rho_{rad} \propto \frac{1}{a^4}$$
उपरोक्त परिणाम एक के साथ उलटा 4 वें शक्ति भिन्नता को दर्शाता है$\rho$।
इसकी शारीरिक रूप से व्याख्या की जा सकती है $a^{-3}$जैसे-जैसे इसकी मात्रा बढ़ती जाती है, उसमें बदलाव आता रहता है। बचा हुआ$a^{-1}$ब्रह्मांड में अंतरिक्ष के विस्तार के कारण फोटॉन द्वारा खोई गई ऊर्जा के रूप में इलाज किया जा सकता है (कॉस्मोलॉजिकल रेडशिफ्ट 1 + z = a -1 )।
निम्नलिखित छवि समय के साथ पदार्थ और विकिरण घनत्व की भिन्नता को दर्शाती है।
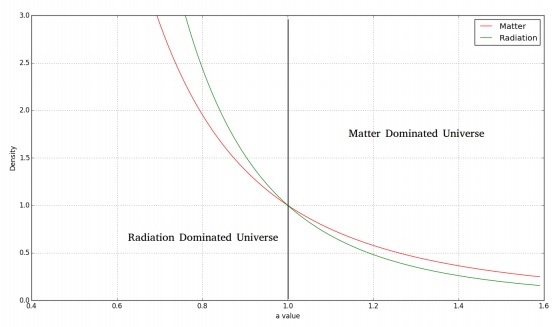
एक फ्लैट, विकिरण प्रभुत्व वाले ब्रह्मांड के लिए, हमारे पास फ्रीडमैन समीकरण इस प्रकार होगा -
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G\rho}{3}$$
$$\left ( \frac{\dot{a}}{a} \right)^2 = \frac{8\pi G}{3}\frac{\rho_0}{a^4}$$
सरलीकरण समीकरण के समाधान को सरल बनाने और लागू करने पर, हमारे पास है -
$$(\dot{a})^2 = \frac{8\pi G\rho_0}{3a^2}$$
$$\Rightarrow a(t) \propto t^{\frac{1}{2}}$$
इस प्रकार, हमारे पास है -
$$a(t) = a_0 \left ( \frac{t}{t_0} \right )^{\frac{1}{2}}$$
उपरोक्त समीकरण से, हम देखते हैं कि पैमाने कारक की वृद्धि की दर धूल भरे ब्रह्मांड की तुलना में छोटी है।
याद दिलाने के संकेत
वर्तमान ब्रह्मांड में प्रचलित विकिरण को तारकीय स्रोतों के लिए बहुत कम जिम्मेदार ठहराया जा सकता है।
धूल भरे ब्रह्मांड के लिए, दबाव शून्य है।
सीएमबी बहुत ठंडा है।
डार्क एनर्जी का क्षेत्र खगोल विज्ञान में एक बहुत ही ग्रे क्षेत्र है क्योंकि यह सभी समीकरणों में एक मुफ्त पैरामीटर है, लेकिन कोई स्पष्ट विचार नहीं है कि यह वास्तव में क्या है।
हम फ्राइडमैन के समीकरणों के साथ शुरुआत करेंगे,
$$\left ( \frac{\dot{a}}{a} \right)^2 = \frac{8\pi G}{3}\rho - \frac{k \ast c^2}{a^2}$$
ब्रह्माण्ड विज्ञान पर अधिकांश प्राथमिक पुस्तकें, वे सभी इस कड़ी से अंधेरे ऊर्जा का वर्णन करने के साथ शुरू करते हैं कि हबल के अवलोकन से पहले, ब्रह्मांड बंद और स्थिर है।
अब, ब्रह्मांड के दाईं ओर स्थिर होने के लिए, दोनों शब्दों का मिलान होना चाहिए और वे शून्य होने चाहिए, लेकिन यदि पहला शब्द दूसरे शब्द से अधिक है, तो ब्रह्मांड स्थिर नहीं होगा, इसलिए आइंस्टीन ने मुक्त पैरामीटर को गिरा दिया ∧ ब्रह्मांड को स्थिर बनाने के लिए क्षेत्र समीकरण में, इसलिए उन्होंने तर्क दिया कि दूसरे कार्यकाल की तुलना में पहला शब्द क्या है, आप हमेशा एक स्थिर ब्रह्मांड प्राप्त कर सकते हैं यदि समीकरण में एक और घटक है, जो डिस की भरपाई कर सकता है- इन दो शब्दों के बीच मेल।
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho - \frac{k \ast c^2}{a^2} + \frac{\wedge}{3}$$
$$\left ( \frac{\ddot{a}}{a} \right ) = -\frac{4 \pi G}{3}\left ( \rho + \frac{3P}{c^2} \right ) + \frac{\wedge}{3}$$
कहाँ पे $P = \rho \ast c^2/3$ तथा $\wedge = \rho \ast c^2$कॉस्मोलॉजिकल पैरामीटर है। (नकारात्मक संकेत केवल आकर्षण के कारण है)
उपरोक्त समीकरण (त्वरण समीकरण) में -
$3P/c^2$ विकिरण के कारण नकारात्मक दबाव है,
$-4\pi G/3$ गुरुत्वाकर्षण के कारण आकर्षण है, और
$\wedge/3$ सकारात्मक योगदान देता है।
तीसरा शब्द एक प्रतिकारक बल के रूप में कार्य करता है क्योंकि समीकरण का एक और हिस्सा आकर्षक है।
समीकरण का भौतिक महत्व है ˙a = 0क्योंकि कोई भी सबूत नहीं था जो दर्शाता है कि ब्रह्मांड का विस्तार हो रहा है। क्या होगा अगर ये दोनों पद एक दूसरे के साथ मेल नहीं खा रहे हैं, इसलिए एक घटक जोड़ना बेहतर है और ऑफसेट के आधार पर हम हमेशा मुक्त पैरामीटर के मूल्य को बदल सकते हैं।
उस समय इस ब्रह्मांड संबंधी मापदंडों के बारे में कोई भौतिक स्पष्टीकरण नहीं था, यही वजह है कि जब 1920 में विस्तार ब्रह्मांड की खोज की गई थी, तो Einstein तुरंत इस स्थिरांक को बाहर फेंकना पड़ा।
इसका स्पष्टीकरण cosmological constant अभी भी उपयोग में है क्योंकि यह ब्रह्मांड के एक अलग संस्करण की व्याख्या करता है, लेकिन इस ब्रह्मांडीय स्थिरांक की परिभाषा, व्याख्या का तरीका समय के साथ बदलता रहा।
अब इस ब्रह्मांडीय स्थिरांक की अवधारणा को कई कारणों से ब्रह्मांड विज्ञान में वापस लाया गया है। इसका एक कारण यह है कि, हमारे पास ब्रह्माण्ड के विभिन्न घटकों (बैरोनिक, डार्क मैटर, विकिरण) के ऊर्जा घनत्व के लिए अवलोकन है, इसलिए हम जानते हैं कि यह पैरामीटर क्या है। का उपयोग करते हुए स्वतंत्र अवलोकनcosmic microwave background दिखाता है कि के = 0।
$$CMB, k=0\: \rho = \rho_c = \frac{3H_0^2}{8\pi G} \approx 10 \: Hydrogen \: atoms.m^{-3}$$
के 0 के लिए, $\rho$ के बराबर होना चाहिए $\rho_c$, लेकिन सब कुछ हम जानते हैं कि अगर हम इसे जोड़ते हैं जो 0 नहीं देता है, जिसका अर्थ है कि कुछ अन्य घटक है जो दर्शाता है कि यह बहुत कम है $\rho_c$।
$$\rho = \rho_b + \rho_{DM} + \rho_{rad} << \rho_c$$
डार्क एनर्जी का एक और सबूत इससे मिलता है Type 1 Supernova Observationजो तब होता है जब श्वेत बौना पदार्थ को ग्रहण करता है और चंद्रशेखर सीमा से अधिक हो जाता है, जो एक बहुत ही सटीक सीमा (M 1.4M) है। अब हर बार जब टाइप 1 सुपरनोवा धमाका होता है, तो हमारे पास एक ही द्रव्यमान होता है जिसका मतलब है कि सिस्टम की कुल बाध्यकारी ऊर्जा समान है और जितनी प्रकाश ऊर्जा हम देख सकते हैं, उतनी ही है।
बेशक, सुपरनोवा प्रकाश बढ़ता है और फिर बेहोश हो जाता है, लेकिन अगर आप चोटी की चमक को मापते हैं तो यह हमेशा वही होता है जो इसे एक मानक उम्मीदवार बनाता है। इसलिए, एक प्रकार 1 सुपरनोवा के साथ हम ब्रह्मांड के ब्रह्माण्ड संबंधी घटक को मापने के लिए इस्तेमाल किया और खगोलविदों ने पाया कि उच्च लाल पारी के साथ सुपरनोवा 30% है - कम लाल पारी सुपरनोवा की तुलना में 40% बेहोशी है और यह समझाया जा सकता है कि क्या कोई गैर है शून्य∧ अवधि।
कॉस्मोलॉजिकल मॉडल में DE (Dark Energy)एक तरल पदार्थ के रूप में माना जाता है, जिसका अर्थ है कि हम इसके लिए राज्य का समीकरण लिख सकते हैं। राज्य का समीकरण वह समीकरण है जो पदार्थ के दो अलग-अलग अवस्थाओं जैसे दबाव, घनत्व, तापमान और आयतन को जोड़ता है।
सामान्य रूप से हम देखते हैं,
$$\frac{8 \pi G}{3}\rho = \frac{\wedge}{3}$$
$$\rho_\wedge = \frac{\wedge}{8\pi G}$$
DE का ऊर्जा घनत्व,
$$\epsilon_\wedge = \rho_\wedge \ast c^2 = \frac{\wedge c^2}{8 \pi G}$$
डार्क एनर्जी डेंसिटी पैरामीटर,
$$\Omega_\wedge = \frac{\rho_\wedge}{\rho_c}$$
$\Omega_\wedge$ महत्वपूर्ण घनत्व के संदर्भ में अंधेरे ऊर्जा का घनत्व है।
$$\rho = \rho_b + \rho_{DM} +\rho_\wedge$$
डार्क एनर्जी के बारे में कई सिद्धांत हैं, जो ब्रह्मांड को दोहरा रहे हैं और जिससे ब्रह्मांड का विस्तार हो रहा है। एक परिकल्पना यह है कि यह गहरी ऊर्जा एक वैक्यूम ऊर्जा घनत्व हो सकती है। मान लीजिए कि अंतरिक्ष खुद कुछ ऊर्जा का प्रसंस्करण कर रहा है और जब आप अंतरिक्ष की इकाई मात्रा के भीतर बायोनिक पदार्थ, डार्क मैटर और विकिरण की मात्रा की गणना करते हैं, तो आप ऊर्जा की मात्रा भी गिन रहे हैं जो अंतरिक्ष से जुड़ी है, लेकिन यह स्पष्ट नहीं है कि अंधेरे ऊर्जा वास्तव में एक वैक्यूम ऊर्जा घनत्व है।
हम जानते हैं कि घनत्व और डार्क फैक्टर और रेडिएशन के पैमाने के बीच संबंध हैं,
$$\rho_m \propto \frac{1}{a^3}$$
$$\rho_m \propto \frac{1}{a^4}$$
हमारे पास घनत्व v / s स्केल फैक्टर प्लॉट है। उसी कथानक में, हम देख सकते हैं$\rho_\wedge$ ब्रह्मांड के विस्तार के साथ एक स्थिर है जो स्केल फैक्टर पर निर्भर नहीं करता है।
निम्न छवि घनत्व और पैमाने कारक के बीच संबंध को दर्शाती है।

‘ρ’ v/s ‘a’(स्केल फैक्टर जो समय से संबंधित है) उसी ग्राफ में, डार्क एनर्जी को एक स्थिरांक के रूप में तैयार किया जाता है। इसलिए, हम वर्तमान ब्रह्मांड में जो भी अंधेरे ऊर्जा को मापते हैं, वह एक स्थिर है।
याद दिलाने के संकेत
कॉस्मिक माइक्रोवेव बैकग्राउंड का उपयोग करने वाली स्वतंत्र टिप्पणियों से पता चलता है कि k = 0।
$\rho_\wedge$ ब्रह्मांड के विस्तार के साथ एक स्थिर है जो स्केल फैक्टर पर निर्भर नहीं करता है।
गुरुत्वाकर्षण भी समय के साथ बदल रहा है जिसे कहा जाता है modified Newtonian dynamics।
इस अध्याय में, हम स्पाइरल गैलेक्सी रोटेशन वक्र्स और डार्क मैटर के साक्ष्य के बारे में चर्चा करेंगे।
डार्क मैटर के बारे में डार्क मैटर एंड ऑब्जर्वेशनल फैक्ट
डार्क मैटर का प्रारंभिक साक्ष्य था study of the Kinematics of Spiral Galaxy।
सूर्य हमारी आकाशगंगा के केंद्र से 30,000 प्रकाशवर्ष दूर है। गांगेय केंद्रित वेग 220 किमी / सेकंड है।
क्यों वेग 220 किमी / एस नहीं है 100 किमी / एस या 500 किमी / एस? वस्तु की गोलाकार गति को क्या नियंत्रित करता है?
त्रिज्या के भीतर संलग्न द्रव्यमान ब्रह्मांड में वेग का पता लगाने में मदद करता है।
मिल्की वे या सर्पिल गैलेक्सी का रोटेशन - डिफरेंशियल रोटेशन
Angular Velocity केंद्र से दूरी के साथ बदलता रहता है।
कक्षीय समय-अवधि केंद्र से दूरी पर निर्भर करती है।
गैलेक्टिक केंद्र के करीब सामग्री में एक छोटी समयावधि होती है और गैलेक्टिक केंद्र से बहुत दूर की सामग्री की एक बड़ी समयावधि होती है।
रोटेशन वक्र
के साथ वेग परिवर्तन की भविष्यवाणी करें Galactic centric radius। वक्र जो वेग देता है वह कक्षीय त्रिज्या के साथ परिवर्तन करता है।
जब हम चीजों को चलते देखते हैं, तो हम सोचते हैं कि यह गुरुत्वाकर्षण है जो रोटेशन को प्रभावित करता है।
जन वितरण त्रिज्या के साथ भिन्न होता है। पदार्थ घनत्व रोटेशन वक्र की भविष्यवाणी करेगा। द्रव्य घनत्व के आधार पर घूर्णन वक्र, जो त्रिज्या के साथ बदलता रहता है।
सतह चमक
हम पैच चुनते हैं और देखते हैं कि प्रकाश कितना बाहर आ रहा है।
पैच से आने वाले प्रकाश की मात्रा को सरफेस ब्राइटनेस कहा जाता है।
इसकी इकाई है mag/arcsec2।
अगर हम पाते हैं कि सतह की चमक त्रिज्या के साथ बदलती है, तो हम पा सकते हैं कि चमकदार पदार्थ त्रिज्या के साथ भिन्न होता है।
$$\mu(r) \propto exp \left( \frac{-r}{h_R} \right )$$
$h_R$ स्केल की लंबाई है। $\mu(r) = \mu_o \ast exp \left( \frac{-r}{h_R} \right )$
$h_R$ दूधिया रास्ते के लिए लगभग 3 kpc है।
सर्पिल आकाशगंगाएं
खगोलविदों को घूर्णी वक्र को समझने के लिए, उन्होंने आकाशगंगाओं को दो घटकों में विभाजित किया है, जो हैं -
- Disk
- Bulge
निम्नलिखित छवि एक केंद्रीय गोलाकार उभार + परिपत्र डिस्क दिखाती है। तार और डिस्क में तारकीय और गैस वितरण अलग है।

सर्पिल आकाशगंगाओं के किनेमैटिक्स
-
किसी भी वस्तु का वृत्ताकार वेग - उभार के लिए होता है (r <Rb)।
$$V^2(r) = G \ast \frac{M(r)}{r}$$
$$M(r) = \frac{4\pi r^3}{3} \ast \rho_b$$
-
डिस्क के लिए - (Rb <r <Rd)
$$V^2(r) = G \ast \frac{M(r)}{r}$$
बुलगे में तारों का लगभग स्थिर घनत्व है।
उभार के भीतर घनत्व स्थिर है (उभार के भीतर की दूरी के साथ नहीं बदल रहा है)।
एक डिस्क में, तारकीय घनत्व त्रिज्या के साथ गिरावट आती है। दायरा बढ़ता है तो चमकदार पदार्थ कम हो जाता है।
थोक में - $V(r) \propto r$
डिस्क में - $V(r) \propto 1/\sqrt{r}$
सर्पिल आकाशगंगाओं के घूर्णी वक्र
के माध्यम से Spectroscopy (आस-पास की आकाशगंगाओं - स्थानिक रूप से आकाशगंगा का समाधान), हम रोटेशन वक्र का उत्पादन करते हैं।
जैसा कि ऊपर उल्लेख किया गया है, हम देखते हैं कि बाहरी क्षेत्रों में रोटेशन वक्र सपाट है, अर्थात बाहरी क्षेत्रों में चीजें तेजी से आगे बढ़ रही हैं, जो आमतौर पर इस रूप में होने की उम्मीद नहीं है।
आंतरिक क्षेत्र की त्रिज्या में वृद्धि के साथ कक्षीय गति बढ़ जाती है, लेकिन यह बाहरी क्षेत्र में समतल होती है।
काला पदार्थ
डार्क मैटर को यूनिवर्स का गैर-चमकदार घटक कहा जाता है। आइए निम्न बिंदुओं के माध्यम से डार्क मैटर के बारे में समझते हैं।
सपाट रोटेशन वक्र्स काउंटर हैं जो हम सर्पिल आकाशगंगाओं में सितारों और गैस के वितरण के लिए देखते हैं।
डिस्क की सतह चमकदारता त्रिज्या के साथ तेजी से गिरती है, यह दर्शाता है कि चमकदार पदार्थ का द्रव्यमान, ज्यादातर तारे, गांगेय केंद्र के आसपास केंद्रित है।
रोटेशन वक्र के समतल होने से पता चलता है कि कुछ त्रिज्या के भीतर आकाशगंगा का कुल द्रव्यमान r में वृद्धि के साथ हमेशा बढ़ रहा है r।
यह केवल तभी समझाया जा सकता है जब इन आकाशगंगाओं में बड़ी मात्रा में अदृश्य गुरुत्वाकर्षण द्रव्यमान है जो विद्युत चुम्बकीय विकिरण को बाहर नहीं दे रहा है।
सर्पिल आकाशगंगाओं के घूर्णन वक्र माप अंधेरे पदार्थ के लिए सबूत के सबसे सम्मोहक सेट में से एक है।
डार्क मैटर के साक्ष्य
गुम द्रव्यमान - चमकदार द्रव्यमान का 10 गुना।
इस डार्क मैटर का अधिकांश भाग आकाशगंगा के प्रभामंडल में होना चाहिए: डिस्क में बड़ी मात्रा में डार्क मैटर ज्वारीय बलों के विरुद्ध डिस्क की दीर्घकालिक स्थिरता को बिगाड़ सकता है।
डिस्क में काले पदार्थ के कुछ छोटे अंश बेरोनिक हो सकते हैं - मंद तारे (भूरे रंग के बौने, काले बौने), और कॉम्पैक्ट तारकीय अवशेष (न्यूट्रॉन स्टार, ब्लैक होल)। लेकिन इस तरह के बेरोनिक डार्क मैटर आकाशगंगाओं में लापता द्रव्यमान के पूर्ण पैमाने की व्याख्या नहीं कर सकते हैं।
डार्क मैटर का घनत्व प्रोफ़ाइल - $M(r) \propto r$ तथा $\rho(r) \propto r^{−2}$।
सर्पिल आकाशगंगाओं के घूर्णन वक्र डेटा उनके प्रभामंडल में वितरित डार्क मैटर के अनुरूप होते हैं।
यह गहरा प्रभामंडल आकाशगंगा के कुल द्रव्यमान का अधिकांश भाग बनाता है।
सभी बायोरोनिक पदार्थ (तारे, तारा समूह, ISM इत्यादि) एक साथ इस गहरे प्रभामंडल की गुरुत्वाकर्षण क्षमता द्वारा धारण किए जाते हैं।
निष्कर्ष
डार्क मैटर को केवल एक सामान्य मामले के साथ उनके गुरुत्वाकर्षण बातचीत के माध्यम से पता लगाया गया है। प्रकाश के साथ कोई बातचीत (कोई विद्युत चुम्बकीय बल) अभी तक नहीं देखी गई है।
Neutrinos- चार्ज कम, कमजोर इंटरेक्शन, लेकिन द्रव्यमान बहुत कम (<0.23 eV) है। डीएम कणों में संरचना निर्माण की व्याख्या करने के लिए ई> 10 ईवी या ऐसा होना चाहिए।
कमजोर अंतःक्रियात्मक विशाल कण (WIMPS) डार्क मैटर का स्रोत हो सकते हैं।
याद दिलाने के संकेत
गैलेक्टिक केंद्र के करीब सामग्री में एक छोटी समयावधि होती है।
बुलगे में तारों का लगभग स्थिर घनत्व है।
डिस्क का सरफेस ल्युमिनोसिटी त्रिज्या के साथ तेजी से गिर जाता है।
डिस्क में बड़ी मात्रा में डार्क मैटर ज्वारीय बलों के खिलाफ डिस्क की दीर्घकालिक स्थिरता को परेशान कर सकता है।
पहले डार्क मैटर के प्रत्यक्ष प्रमाण मिले Frids Ricky। उन्होंने कुछ अवलोकन किए जिनसे पहली बार काले पदार्थ का पता चला। उनकी टिप्पणियों ने आकाशगंगा समूह के भीतर समग्र गति पर विचार किया।
विस्तारित वस्तुएं आकाशगंगा समूह हैं और उन्हें बाध्य संरचना माना जाता है। ये आकाशगंगाएं क्लस्टर केंद्र के संबंध में आगे बढ़ रही हैं, लेकिन उड़ान नहीं भरती हैं। हम आकाशगंगा के समग्र गति को देखते हैं।
मान्यता: वेग, पराधीनता के प्रतिनिधि हैं
हर आकाशगंगा में क्लस्टर के भीतर अपनी उचित गति होगी और Hubble Flow Component। छोटी आकाशगंगाएँ छोटी हैं, अधिकांश प्रकाश M31 और MW से आती हैं, कई बौनी आकाशगंगाएँ हैं। हमारे कच्चे विश्लेषण के लिए, हम केवल M31 और MW का उपयोग कर सकते हैं और स्थानीय समूह के गतिशील द्रव्यमान का मूल्यांकन कर सकते हैं।
हमारे और M31 के बीच एक सापेक्ष वेग है। यह कच्चा है, लेकिन यह सच है। कहानी बहुत पहले शुरू होती है जब M31 और MW एक-दूसरे के करीब होते थे, क्योंकि वे एक क्लस्टर के सदस्य थे जो एक-दूसरे से दूर जा रहे थे। कुछ समय बाद वे अधिकतम अलगाव तक पहुंच जाते हैं, फिर एक दूसरे के करीब आते हैं।
हम कहते हैं कि अधिकतम अलगाव जो कभी भी पहुंच सकता है $r_{max}$। अब उनके पास एक अलगाव हैr। लश्करMMW और M31 का संयुक्त द्रव्यमान हो। हम नहीं जानते कि कब$r_{max}$ पहुंच गया।
$$\frac{GM}{r_{max}} = \:Potential \: at \:r_{max}$$
जब ये आकाशगंगाएँ किसी त्वरित r पर एक दूसरे के करीब आ रही थीं, तब सिस्टम की ऊर्जा होगी -
$$\frac{1}{2}\sigma^2 = \frac{GM}{r} = \frac{GM}{r_{max}}$$
ocity दोनों आकाशगंगाओं का सापेक्ष वेग है। M केवल द्रव्यमान घटाया जाता है, लेकिन परीक्षण द्रव्यमान 1. but दूरी पर किसी भी वस्तु का वेग है rक्लस्टर के केंद्र से। हमारा मानना है कि यह क्लस्टर गतिशील समीकरण में है क्योंकि वायरल प्रमेय धारण करता है। इसलिए, आकाशगंगाएँ विभिन्न वेग के साथ नहीं आ सकती हैं।
इन आकाशगंगाओं को अधिकतम दूरी तक पहुंचने में कितना समय लगेगा?
इसे समझने के लिए, हम निम्नलिखित समीकरण पर विचार करें।
$$\frac{1}{2}\left ( \frac{dr}{dt} \right )^2 = \frac{GM}{r} - \frac{GM}{r_{max}}$$
$$t_{max} = \int_{0}^{r_{max}} dt = \int_{0}^{r_{max}} \frac{dr}{\sqrt{2GM}}\left ( \frac{1}{r} - \frac{1}{r_{max}} \right )^2$$
$$t_{max} = \frac{\pi r_{max}^{\frac{3}{2}}}{2\sqrt{2GM}}$$
जहां, M = स्थानीय समूह का गतिशील द्रव्यमान। शुरू से टकराने के अंत तक का कुल समय$2t_{max}$। इसलिए,
$$2t_{max} = t_0 + \frac{D}{\sigma}$$
तथा $t_0$ ब्रह्मांड की वर्तमान आयु है।
अगर वास्तविक है $t_{max} < RHS$, तो हम समय के लिए एक कम सीमा है। $D/\sigma$वह समय है जब वे फिर से टकराएंगे। यहाँ, हमने σ को स्थिर माना है।
$$t_{max} = \frac{t_0}{2} + \frac{D}{2\sigma}$$
$$r_{max} = t_{max} \times \sigma = 770K_{pc}$$
यहाँ, MW और M31 के बीच, = सापेक्ष वेग।
$$M_{dynamic} = 3 \times 10^{12}M_0$$
$$M_{MW}^{lum} = 3 \times 10^{10}M_0$$
$$M_{M31}^{lum} = 3 \times 10^{10}M_0$$
लेकिन व्यावहारिक रूप से, क्लस्टर के भीतर प्रत्येक आकाशगंगा पर विचार करते हुए गतिशील द्रव्यमान पाया जाता है। लापता द्रव्यमान डार्क मैटर है औरFrids Rickyदेखा कि कोमा क्लस्टर में आकाशगंगाएं बहुत तेजी से आगे बढ़ रही हैं। उन्होंने कहा कि न्यूट्रॉन सितारों की खोज के बाद न्यूट्रॉन सितारों के अस्तित्व की भविष्यवाणी की और सुपरनोवा को खोजने के लिए पालोमर टेलीस्कोप का इस्तेमाल किया।
याद दिलाने के संकेत
पहले डार्क मैटर के प्रत्यक्ष प्रमाण मिले Frids Ricky।
विस्तारित वस्तुएं आकाशगंगा समूह हैं और उन्हें माना जाता है bound structures।
Dynamic mass क्लस्टर के भीतर हर आकाशगंगा पर विचार करके पाया जाता है।
इस अध्याय में, हम घनत्व और हबल मापदंडों के बारे में चर्चा करेंगे।
हबल पैरामीटर
हबल पैरामीटर को निम्नानुसार परिभाषित किया गया है -
$$H(t) \equiv \frac{da/dt}{a}$$
जो मापता है कि स्केल फैक्टर कितनी तेजी से बदलता है। अधिक सामान्यतः, स्केल कारक का विकास फ्राइडमैन समीकरण द्वारा निर्धारित किया जाता है।
$$H^2(t) \equiv \left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho - \frac{kc^2}{a^2} + \frac{\wedge}{3}$$
कहाँ पे, ∧ एक ब्रह्मांडीय स्थिरांक है।
एक सपाट ब्रह्मांड के लिए, k = 0, इसलिए फ्राइडमैन समीकरण बन जाता है -
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho + \frac{\wedge}{3}$$
ब्रह्माण्ड के वर्चस्व वाले पदार्थ के लिए, घनत्व भिन्न होता है -
$$\frac{\rho_m}{\rho_{m,0}} = \left ( \frac{a_0}{a} \right )^3 \Rightarrow \rho_m = \rho_{m,0}a^{-3}$$
और, एक विकिरणित ब्रह्मांड के घनत्व के रूप में घनत्व भिन्न होता है -
$$\frac{\rho_{rad}}{\rho_{rad,0}} = \left ( \frac{a_0}{a} \right )^4 \Rightarrow \rho_{rad} = \rho_{rad,0}a^{-4}$$
वर्तमान में, हम एक ब्रह्मांड के प्रभुत्व वाले पदार्थ में रह रहे हैं। इसलिए, विचार कर$\rho ≡ \rho_m$, हमें मिलता है -
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho_{m,0}a^{-3} + \frac{\wedge}{3}$$
ब्रह्माण्ड संबंधी स्थिरांक और श्याम ऊर्जा घनत्व निम्नानुसार हैं -
$$\rho_\wedge = \frac{\wedge}{8 \pi G} \Rightarrow \wedge = 8\pi G\rho_\wedge$$
इससे हमें प्राप्त होता है -
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho_{m,0}a^{-3} + \frac{8 \pi G}{3} \rho_\wedge$$
इसके अलावा, महत्वपूर्ण घनत्व और हबल के स्थिरांक निम्नानुसार हैं -
$$\rho_{c,0} = \frac{3H_0^2}{8 \pi G} \Rightarrow \frac{8\pi G}{3} = \frac{H_0^2}{\rho_{c,0}}$$
इससे हमें प्राप्त होता है -
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{H_0^2}{\rho_{c,0}}\rho_{m,0}a^{-3} + \frac{H_0^2}{\rho_{c,0}}\rho_\wedge$$
$$\left ( \frac{\dot{a}}{a} \right )^2 = H_0^2\Omega_{m,0}a^{-3} + H_0^2\Omega_{\wedge,0}$$
$$(\dot{a})^2 = H_0^2\Omega_{m,0}a^{-1} + H_0^2\Omega_{\wedge,0}a^2$$
$$\left ( \frac{\dot{a}}{H_0} \right )^2 = \Omega_{m,0}\frac{1}{a} + \Omega_{\wedge,0}a^2$$
$$\left ( \frac{\dot{a}}{H_0} \right )^2 = \Omega_{m,0}(1+z) + \Omega_{\wedge,0}\frac{1}{(1+z)^2}$$
$$\left ( \frac{\dot{a}}{H_0} \right)^2 (1+z)^2 = \Omega_{m,0}(1+z)^3 + \Omega_{\wedge,0}$$
$$\left ( \frac{\dot{a}}{H_0} \right)^2 \frac{1}{a^2} = \Omega_{m,0}(1 + z)^3 + \Omega_{\wedge,0}$$
$$\left ( \frac{H(z)}{H_0} \right )^2 = \Omega_{m,0}(1+z)^3 + \Omega_{\wedge,0}$$
यहाँ, $H(z)$लाल पारी पर निर्भर हबल पैरामीटर है। यह विकिरण घनत्व पैरामीटर को शामिल करने के लिए संशोधित किया जा सकता है$\Omega_{rad}$ और वक्रता घनत्व पैरामीटर $\Omega_k$। संशोधित समीकरण है -
$$\left ( \frac{H(z)}{H_0} \right )^2 = \Omega_{m,0}(1+z)^3 + \Omega_{rad,0}(1+z)^4+\Omega_{k,0}(1+z)^2+\Omega_{\wedge,0}$$
$$Or, \: \left ( \frac{H(z)}{H_0} \right)^2 = E(z)$$
$$Or, \: H(z) = H_0E(z)^{\frac{1}{2}}$$
कहाँ पे,
$$E(z) \equiv \Omega_{m,0}(1 + z)^3 + \Omega_{rad,0}(1+z)^4 + \Omega_{k,0}(1+z)^2+\Omega_{\wedge,0}$$
इससे पता चलता है कि हबल पैरामीटर समय के साथ बदलता रहता है।
के लिए Einstein-de Sitter ब्रम्हांड, $\Omega_m = 1, \Omega_\wedge = 0, k = 0$।
इन मूल्यों को रखते हुए, हम प्राप्त करते हैं -
$$H(z) = H_0(1+z)^{\frac{3}{2}}$$
जो आइंस्टीन-डी सिटर ब्रह्मांड के लिए हबल पैरामीटर का समय विकास दर्शाता है।
घनत्व पैरामीटर
घनत्व पैरामीटर, $\Omega$, को वास्तविक (या मनाया गया) घनत्व के अनुपात के रूप में परिभाषित किया गया है महत्वपूर्ण घनत्व $\rho_c$। किसी भी मात्रा के लिए$x$ इसी घनत्व पैरामीटर, $\Omega_x$ गणितीय रूप से व्यक्त किया जा सकता है -
$$\Omega_x = \frac{\rho_x}{\rho_c}$$
विचाराधीन विभिन्न मात्राओं के लिए, हम निम्नलिखित घनत्व मापदंडों को परिभाषित कर सकते हैं।
| क्र.सं. | मात्रा | घनत्व पैरामीटर |
|---|---|---|
| 1 | बेरियान कणिकाओं | $\Omega_b = \frac{\rho_b}{\rho_c}$ |
| 2 | पदार्थ (बैरोनिक + डार्क) | $\Omega_m = \frac{\rho_m}{\rho_c}$ |
| 3 | काली ऊर्जा | $\Omega_\wedge = \frac{\rho_\wedge}{\rho_c}$ |
| 4 | विकिरण | $\Omega_{rad} = \frac{\rho_{rad}}{\rho_c}$ |
जहां प्रतीकों के अपने सामान्य अर्थ हैं।
याद दिलाने के संकेत
स्केल फैक्टर का विकास किसके द्वारा निर्धारित किया जाता है Friedmann Equation।
H(z) लाल पारी पर निर्भर हबल पैरामीटर है।
Hubble Parameter समय के साथ बदलता रहता है।
Density Parameter महत्वपूर्ण घनत्व के लिए वास्तविक (या मनाया) घनत्व के अनुपात के रूप में परिभाषित किया गया है।
जैसा कि पहले अध्यायों में चर्चा की गई है, हबल पैरामीटर का समय विकास किसके द्वारा दिया गया है?
$$H(z) = H_0E(z)^{\frac{1}{2}}$$
कहाँ पे z लाल पारी है और E(Z) है -
$$E(z) \equiv \Omega_{m,0}(1+z)^3 + \Omega(1+z)^4 +\Omega_{k,0}(1+z)^2 + \Omega^{\wedge,0}$$
यदि ब्रह्माण्ड का विस्तार स्थिर है, तो ब्रह्मांड की सही आयु इस प्रकार दी गई है -
$$t_H = \frac{1}{H_0}$$
यदि बात ब्रह्मांड के वर्चस्व वाले आइंस्टीन डेसिटर ब्रह्माण्ड की करें तो ब्रह्माण्ड की सही आयु किसके द्वारा दी गई है?
$$t_H = \frac{2}{3H_0}$$
स्केल और रेडशिफ्ट द्वारा परिभाषित किया गया है -
$$a=\frac{a_0}{1+z}$$
ब्रह्माण्ड संबंधी पैरामीटर के संदर्भ में ब्रह्मांड की आयु निम्नानुसार है।
हबल पैरामीटर द्वारा दिया गया है -
$$H = \frac{\frac{da}{dt}}{a}$$
विभेद करते हुए, हम प्राप्त करते हैं -
$$da = \frac{-dz}{(1+z)^2}$$
कहाँ पे a0 = 1 (स्केल फैक्टर का वर्तमान मूल्य)
$$\frac{\mathrm{d} a}{\mathrm{d} t} = \frac{-1}{(1+z)^2}$$
$$\frac{\mathrm{d} a}{\mathrm{d} t} = \frac{\mathrm{d} a}{\mathrm{d} t}\frac{\mathrm{d} z}{\mathrm{d} t}$$
$$H = \frac{\dot{a}}{a} = \frac{\mathrm{d} a}{\mathrm{d} t}\frac{\mathrm{d} z}{\mathrm{d} t} \frac{1+z}{1}$$
$$\frac{\dot{a}}{a} = \frac{-1}{1+z}\frac{\mathrm{d} z}{\mathrm{d} t}\frac{1}{1}$$
$$H(z) = H_0E(z)^{\frac{1}{2}}$$
$$dt = \frac{-dz}{H_0E(z)^{\frac{1}{2}}(1+z)}$$
यदि हम ब्रह्मांड की आयु किसी भी दिए गए लाल रंग में खोजना चाहते हैं ‘z’ तब -
$$t(z) = \frac{1}{H_0}\int_{\infty}^{z_1} \frac{-1}{E(z)^{\frac{1}{2}}(1+z)}dz$$
कहाँ पे k वक्रता घनत्व पैरामीटर और है -
$$E(z) \equiv \Omega_{m,0}(1+z)^3 + \Omega_{rad,0}(1+z)^4 + \Omega_{k,0}(1+z)^2 + \Omega_{\wedge,0}$$
ब्रह्मांड की वर्तमान आयु की गणना करने के लिए z1 = 0।
$$t(z=0) = t_{age} = t_0 = \frac{1}{H_0}\int_{\infty}^{z_1} \frac{-1}{E(z)^{\frac{1}{2}}(1+z)}dz$$
आइंस्टीन डिसिटर मॉडल के लिए, $\Omega_m = 1$, $\Omega_{rad} = 0$, $\Omega_k = 0$, $\Omega_\wedge = 0$ब्रह्मांड की आयु के लिए समीकरण बन जाता है -
$$t_{age} = \frac{1}{H_0}\int_{0}^{\infty} \frac{1}{(1+z)^{\frac{5}{2}}}dz$$
अभिन्न को हल करने के बाद, हम प्राप्त करते हैं -
$$t_H = \frac{2}{3H_0}$$
रात का आकाश जैसे है Cosmic Time Machine.जब भी हम किसी दूर के ग्रह, तारे या आकाशगंगा का निरीक्षण करते हैं, तो हम इसे उसी तरह देख रहे हैं जैसे कि यह घंटों, सदियों या सदियों पहले था। ऐसा इसलिए है क्योंकि प्रकाश एक परिमित गति (प्रकाश की गति) पर यात्रा करता है और ब्रह्मांड में बड़ी दूरी को देखते हुए, हम वस्तुओं को वैसा नहीं देखते हैं जैसा कि वे अब हैं, लेकिन जब वे प्रकाश उत्सर्जित होते थे। समय बीतने के बीच - जब हम पृथ्वी पर प्रकाश का पता लगाते हैं और जब यह मूल रूप से स्रोत द्वारा उत्सर्जित होता है, तो इसे किस नाम से जाना जाता है?Lookback Time (tL(z1))।
तो, लुकबैक समय किसके द्वारा दिया जाता है -
$$t_1(z_1) = t_0-t(z_1)$$
आइंस्टीन डेसिटर यूनिवर्स का लुकबैक समय है -
$$t_L(z) = \frac{2}{3H_0}\left [ 1- \frac{1}{(1+z)^{\frac{3}{2}}} \right ]$$
याद दिलाने के संकेत
जब भी हम किसी दूर के ग्रह, तारे या आकाशगंगा का निरीक्षण करते हैं, तो हम इसे उसी तरह देख रहे हैं जैसे कि यह घंटों, सदियों या सदियों पहले था।
समय बीतने के बीच - जब हम पृथ्वी पर यहाँ प्रकाश का पता लगाते हैं और जब यह मूल रूप से स्रोत द्वारा उत्सर्जित होता है, तो इसे देखने के समय के रूप में जाना जाता है।
इस अध्याय में, हम समझेंगे कि कोणीय व्यास दूरी क्या है और यह कॉस्मोलॉजी में कैसे मदद करता है।
वर्तमान ब्रह्मांड के लिए -
$\Omega_{m,0} \: = \: 0.3$
$\Omega_{\wedge,0} \: = \: 0.69$
$\Omega_{rad,0} \: = \: 0.01$
$\Omega_{k,0} \: = \: 0$
हमने अब तक दो प्रकार की दूरियों का अध्ययन किया है -
Proper distance (lp) - फोटॉनों कि दूरी स्रोत से यात्रा करने के लिए हमें, यानी Instantaneous distance।
Comoving distance (lc) - एक अंतरिक्ष में वस्तुओं के बीच की दूरी जो विस्तार नहीं करती है, अर्थात distance in a comoving frame of reference।
रेडशिफ्ट के कार्य के रूप में दूरी
एक आकाशगंगा पर विचार करें जो समय पर एक फोटॉन को विकिरण करती है t1 जिसे पर्यवेक्षक द्वारा पता लगाया जाता है t0। हम आकाशगंगा के लिए उचित दूरी लिख सकते हैं -
$$l_p = \int_{t_1}^{t_0} cdt$$
आकाशगंगा के लाल होने दें z,
$$\Rightarrow \frac{\mathrm{d} z}{\mathrm{d} t} = -\frac{1}{a^2}\frac{\mathrm{d} a}{\mathrm{d} t}$$
$$\Rightarrow \frac{\mathrm{d} z}{\mathrm{d} t} = -\frac{\frac{\mathrm{d} a}{\mathrm{d} t}}{a}\frac{1}{a}$$
$$\therefore \frac{\mathrm{d} z}{\mathrm{d} t} = -\frac{H(z)}{a}$$
अब, किसी भी समय आकाशगंगा की दूरी कम करना t होगा -
$$l_c = \frac{l_p}{a(t)}$$
$$l_c = \int_{t_1}^{t_0} \frac{cdt}{a(t)}$$
Z के संदर्भ में,
$$l_c = \int_{t_0}^{t_1} \frac{cdz}{H(z)}$$
दूरी खोजने के दो तरीके हैं, जो इस प्रकार हैं -
फ्लक्स-ल्यूमिनोसिटी संबंध
$$F = \frac{L}{4\pi d^2}$$
कहाँ पे d स्रोत पर दूरी है।
एक स्रोत की कोणीय व्यास दूरी
यदि हम किसी स्रोत के आकार को जानते हैं, तो इसकी कोणीय चौड़ाई हमें पर्यवेक्षक से इसकी दूरी बताएगी।
$$\theta = \frac{D}{l}$$
कहाँ पे l स्रोत की कोणीय व्यास दूरी है।
θ स्रोत का कोणीय आकार है।
D स्रोत का आकार है।
आकार D और कोणीय आकार की एक आकाशगंगा पर विचार करें dθ।
हम जानते हैं कि,
$$d\theta = \frac{D}{d_A}$$
$$\therefore D^2 = a(t)^2(r^2 d\theta^2) \quad \because dr^2 = 0; \: d\phi ^2 \approx 0$$
$$\Rightarrow D = a(t)rd\theta$$
बदलना r सेवा rcआकाशगंगा की दूरी, हमारे पास है -
$$d\theta = \frac{D}{r_ca(t)}$$
यहां, यदि हम चुनते हैं t = t0, हम आकाशगंगा के लिए वर्तमान दूरी को मापते हैं। परंतुDको फोटॉन के उत्सर्जन के समय मापा जाता है। इसलिए, उपयोग करकेt = t0, हमें आकाशगंगा के लिए एक बड़ी दूरी मिलती है और इसलिए इसके आकार को कम करके आंका जाता है। इसलिए हमें समय का सदुपयोग करना चाहिएt1।
$$\therefore d\theta = \frac{D}{r_ca(t_1)}$$
पिछले परिणाम के साथ तुलना करने पर, हमें यह मिलता है -
$$d_\wedge = a(t_1)r_c$$
$$r_c = l_c = \frac{d_\wedge}{a(t_1)} = d_\wedge(1+z_1) \quad \because 1+z_1 = \frac{1}{a(t_1)}$$
इसलिए,
$$d_\wedge = \frac{c}{1+z_1} \int_{0}^{z_1} \frac{dz}{H(z)}$$
dA ऑब्जेक्ट के लिए कोणीय व्यास दूरी है।
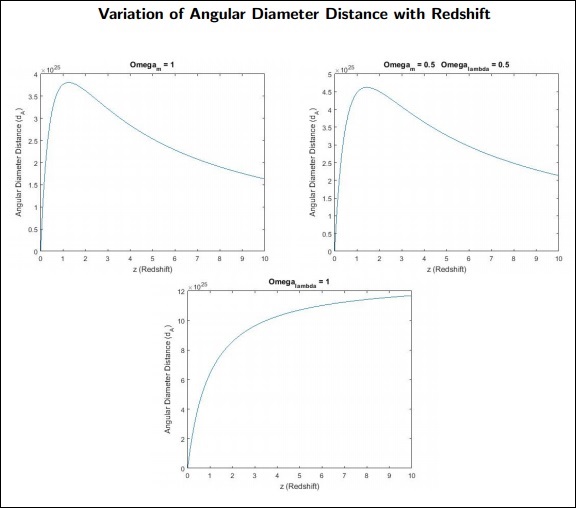
याद दिलाने के संकेत
यदि हम किसी स्रोत के आकार को जानते हैं, तो इसकी कोणीय चौड़ाई हमें पर्यवेक्षक से इसकी दूरी बताएगी।
उचित दूरी वह दूरी है जो फोटॉन स्रोत से यात्रा करते हैं।
Comoving दूरी एक अंतरिक्ष में वस्तुओं के बीच की दूरी है जो विस्तार नहीं करती है।
जैसा कि पिछले अध्याय में चर्चा की गई है, लाल पारी में एक स्रोत के लिए कोणीय व्यास की दूरी z द्वारा दिया गया है -
$$d_\wedge (z_{gal}) = \frac{c}{1+z_{gal}}\int_{0}^{z_{gal}} \frac{1}{H(z)}dz$$
$$d_\wedge(z_{gal}) = \frac{r_c}{1+z_{gal}}$$
कहाँ पे $r_c$ दूरी पर है।
ल्यूमिनोसिटी दूरी कॉस्मोलॉजी पर निर्भर करती है और इसे उस दूरी के रूप में परिभाषित किया जाता है जिस पर मनाया प्रवाह होता है f एक वस्तु से है।
अगर आंतरिक चमक $d_L$ एक दूर की वस्तु ज्ञात है, हम प्रवाह को मापकर इसकी चमक की गणना कर सकते हैं $f$ जिसके द्वारा निर्धारित किया जाता है -
$$d_L(z) = \sqrt{\frac{L}{4\pi f}}$$
फोटॉन एनर्जी रेड शिफ्ट हो जाती है।
$$\frac{\lambda_{obs}}{\lambda_{emi}} = \frac{a_0}{a_e}$$
कहाँ पे $\lambda_{obs}, \lambda_{emi}$ मनाया और उत्सर्जित तरंग लंबाई और हैं $a_0, a_e$ इसी पैमाने के कारक हैं।
$$\frac{\Delta t_{obs}}{\Delta t_{emi}} = \frac{a_0}{a_e}$$
कहाँ पे $\Delta_t{obs}$ फोटॉन समय अंतराल के रूप में मनाया जाता है, जबकि $\Delta_t{emi}$ समय अंतराल है जिस पर वे उत्सर्जित होते हैं।
$$L_{emi} = \frac{nhv_{emi}}{\Delta t_{emi}}$$
$$L_{obs} = \frac{nhv_{obs}}{\Delta t_{obs}}$$
$\Delta t_{obs}$ से अधिक समय लगेगा $\Delta t_{emi}$ क्योंकि डिटेक्टर को सभी फोटॉनों को प्राप्त करना चाहिए।
$$L_{obs} = L_{emi}\left ( \frac{a_0}{a_e} \right )^2$$
$$L_{obs} < L_{emi}$$
$$f_{obs} = \frac{L_{obs}}{4\pi d_L^2}$$
एक गैर-विस्तार वाले ब्रह्मांड के लिए, चमकदार दूरी कॉमोविंग दूरी के समान है।
$$d_L = r_c$$
$$\Rightarrow f_{obs} = \frac{L_{obs}}{4\pi r_c^2}$$
$$f_{obs} = \frac{L_{emi}}{4 \pi r_c^2}\left ( \frac{a_e}{a_0} \right )^2$$
$$\Rightarrow d_L = r_c\left ( \frac{a_0}{a_e} \right )$$
हम प्रकाशमान दूरी पा रहे हैं $d_L$ उत्सर्जक वस्तु की चमक की गणना के लिए $L_{emi}$ -
Interpretation - अगर हम लाल पारी को जानते हैं z किसी भी आकाशगंगा में, हम पता लगा सकते हैं $d_A$ और उससे हम गणना कर सकते हैं $r_c$। यह पता लगाने के लिए उपयोग किया जाता है$d_L$।
अगर $d_L ! = r_c(a_0/a_e)$, तो हम से Lemi नहीं मिल सकता है $f_{obs}$।
चमक दूरी के बीच संबंध $d_L$ और कोणीय व्यास दूरी $d_A.$
हम जानते हैं कि -
$$d_A(z_{gal}) = \frac{d_L}{1+z_{gal}}\left ( \frac{a_0}{a_e} \right )$$
$$d_L = (1 + z_{gal})d_A(z_{gal})\left ( \frac{a_0}{a_e} \right )$$
फोटॉन उत्सर्जित होने पर स्केल कारक - द्वारा दिया जाता है
$$a_e = \frac{1}{(1+z_{gal})}$$
वर्तमान ब्रह्मांड के लिए स्केल कारक है -
$$a_0 = 1$$
$$d_L = (1 + z_{gal})^2d_\wedge(z_{gal})$$
जिसे या तो चुनना है $d_L$ या $d_A$?
ज्ञात आकार की एक आकाशगंगा के लिए और यह कितना बड़ा है, इसकी गणना के लिए लाल बदलाव $d_A$ प्रयोग किया जाता है।
यदि किसी दी गई स्पष्ट परिमाण की आकाशगंगा है, तो यह पता लगाने के लिए कि वह कितनी बड़ी है, $d_L$ प्रयोग किया जाता है।
Example - यदि यह दिया जाता है कि दो लाल आकाशगंगाएं बराबर लाल शिफ्ट (z = 1) और आकाश के विमान में वे अलग हो जाती हैं 2.3 arc sec फिर उन दोनों के बीच अधिकतम शारीरिक अलगाव क्या है?
इसके लिए, का उपयोग करें $d_A$ निम्नानुसार है -
$$d_A(z_{gal}) = \frac{c}{1+z_{gal}}\int_{0}^{z_{gal}} \frac{1}{H(z)}dz$$
जहाँ z = 1 प्रतिस्थापन H (z) आकाशगंगाओं के ब्रह्माण्ड संबंधी मापदंडों के आधार पर है।
याद दिलाने के संकेत
चमक दूरी पर निर्भर करता है cosmology।
अगर आंतरिक चमक $d_L$ एक दूर की वस्तु ज्ञात है, हम प्रवाह को मापकर इसकी चमक की गणना कर सकते हैं f।
एक गैर-विस्तार वाले ब्रह्मांड के लिए, चमक दूरी एक समान है comoving distance।
चमकदार दूरी हमेशा से अधिक होती है Angular Diameter Distance।
किसी भी रेडशिफ्ट (z) के लिए, हमारे पास दूरी के लिए दो मूल्य हैं -
- कोणीय व्यास दूरी (डी ए )
- चमक दूरी (डी एल )
ब्रह्मांड में "कॉस्मोलॉजिकल" दूरी की कोई अनूठी परिभाषा नहीं है। दूरी का चुनाव आवेदन के उद्देश्य और सुविधा पर निर्भर करता है।
किसी वस्तु का कोणीय आकार रेडशिफ्ट के साथ कैसे बदलता है, इसकी भविष्यवाणी की प्रवृत्ति का परीक्षण करने के लिए, आकाश में एक मानक आकार के यार्डस्टिक की आवश्यकता होती है। यह एक वस्तु होनी चाहिए जो -
बहुत चमकदार है, ताकि यह z> 1 पर पता लगाया जा सके।
बहुत बड़ा है, ताकि हम इसके कोणीय आकार को हल कर सकें।
कॉस्मोलॉजिकल रूप से महत्वपूर्ण समय पर रूपात्मक रूप से विकसित नहीं हुआ है (z onds 1 लगभग 7 Gyr के एक बार वापस देखने से मेल खाता है)।
कुछ वस्तुएं (जैसे सी डी आकाशगंगाएं) पहले दो मानदंडों को पूरा करती हैं। लेकिन लगभग हर वस्तु समय के साथ रूपात्मक रूप से विकसित होती पाई जाती है। सामान्य तौर पर, खगोलीय पिंड (विस्तारित स्रोत) अतीत में आंतरिक रूप से छोटे होते हैं क्योंकि वे अभी भी बन रहे हैं।
चमकदार दूरी
ल्यूमिनोसिटी दूरी कॉस्मोलॉजी पर निर्भर करती है। ब्रह्माण्ड विज्ञान पर प्रकाश की दूरी की निर्भरता इसे ब्रह्माण्ड संबंधी मापदंडों का एक उपयोगी उपाय बनाती है।
ब्रह्माण्ड संबंधी मापदंडों का अनुमान लगाया जा सकता है यदि हम एक मानक मोमबत्ती पा सकते हैं जो आंतरिक रूप से विकसित नहीं होती है और स्थानीय से उच्च रेडशिफ्ट ब्रह्मांड में मौजूद होती है।
एक मानक मोमबत्ती वह है जो स्रोत से स्रोत तक इसकी चमक में भिन्न नहीं होती है। आधार यह है कि मानक मोमबत्तियों की अनुमानित चमक में कोई अंतर कॉस्मोलॉजी के कारण होना चाहिए। ऐसी ही एक मोमबत्ती है टाइप आईए सुपरनोवा।
टाइप 1a सुपरनोवा (SNe)
ये एक बाइनरी सिस्टम में अपने साथी, एक लाल विशाल या इसी तरह के मुख्य अनुक्रम स्टार से पर्याप्त द्रव्यमान अभिवृद्धि के बाद एक सफेद बौने के विस्फोट का परिणाम हैं। लाल विशाल श्वेत बौने की रोश पालि की दूरी के करीब आने के बाद, द्रव्यमान स्थानांतरण शुरू होता है और अंततः सफेद बौना बड़ी मात्रा में ऊर्जा देता है, जिससे कोई कोर पीछे नहीं रहता। इन्हें टाइप 1 ए सुपरनोवा कहा जाता है। एक आकाशगंगा में टाइप 1 ए सुपरनोवा विस्फोट की विशिष्ट दर प्रति शताब्दी 1 है।
टाइप 1 ए एसएन की खोज विभिन्न टीमों के साथ चल रही है -
- हाई जेड सुपरनोवा सर्च टीम (ब्रायन श्मिट, एडम रीस एट अल।)
- सुपरनोवा कॉस्मोलॉजी प्रोजेक्ट (शाऊल पर्लमटर एट अल।)
एक और रिसर्च टीम को बुलाया गया है Carnegie Supernovae Project जिन्होंने समान परिणाम दिए हैं।
विभिन्न टीमों के परिणामों की समानता टाइप 1 ए एसएन के ब्रह्मांड संबंधी प्रकृति को दर्शाती है। इसलिए, वे कुशल मानक मोमबत्तियाँ हैं।
याद दिलाने के संकेत
ब्रह्मांड में "कॉस्मोलॉजिकल" दूरी की कोई अनूठी परिभाषा नहीं है।
कोणीय व्यास दूरी और चमक दूरी का सबसे अधिक उपयोग किया जाता है।
एक मानक मोमबत्ती वह है जो स्रोत से स्रोत तक इसकी चमक में भिन्न नहीं होती है।
टाइप 1 ए एसएन एक मानक मोमबत्ती होने के मानदंड को संतुष्ट करता है।
CMB (कॉस्मिक माइक्रोवेव बैकग्राउंड) अनिवार्य रूप से उस समय के फोटॉनों द्वारा गठित किया जाता है जब पदार्थ और विकिरण संतुलन में थे। 1920 के दशक तक, एक विस्तारित ब्रह्मांड के विचार को स्वीकार किया गया था और कई सवालों के जवाब दे सकता था। लेकिन भारी तत्वों की प्रचुरता और बहुतायत के बारे में सवाल अनुत्तरित छोड़ दिए गए थे। इसके अलावा, विस्तारित ब्रह्मांड का तात्पर्य है कि पदार्थ का घनत्व घटकर 0 हो जाना चाहिए।
1948 में, जॉर्ज गैमोव और राल्फ अल्फ़र ने भारी तत्वों की उत्पत्ति और "बिग बैंग" का उपयोग करते हुए बहुतायत से समझाया। उन्होंने रॉबर्ट हरमन के साथ "राहत विकिरण" या "बिग बैंग" से शेष विकिरण के अस्तित्व की भविष्यवाणी की। इस अवशेष विकिरण के लिए अनुमानित तापमान 50-6 K के बीच था। 1965 में, रॉबर्ट डिके, जिम पीबल्स और डेविड विल्किंसन के साथ-साथ Amo Perizias 'रिसर्च ग्रुप ने CMB का प्रयोगात्मक रूप से पता लगाया।
प्रारंभिक ब्रह्मांड बहुत गर्म था और मामले के तटस्थ रहने के लिए ऊर्जा बहुत अधिक थी। इसलिए, पदार्थ आयनित रूप में था -Plasma। विकिरण (फोटॉन) और पदार्थ (प्लाज्मा) ने मुख्य रूप से निम्नलिखित तीन प्रक्रियाओं के माध्यम से बातचीत की।
Compton Scattering - (मेजर इंटरेक्शन प्रोसेस) हाई एनर्जी फोटॉन और लो एनर्जी चार्जेड पार्टिकल के बीच इनेलोस्टिक स्कैटरिंग।
Thomson Scattering - एक मुक्त आवेशित कण द्वारा फोटान का लोचदार बिखरना।
Inverse Compton Scattering- उच्च ऊर्जा चार्ज कण और कम ऊर्जा फोटॉन। इन अंतःक्रियाओं के परिणामस्वरूप पदार्थ और विकिरण थर्मल संतुलन में थे।
थर्मल संतुलन
थर्मल संतुलन में, विकिरण का पालन करता है Planck Distribution of Energy,
$$B_v(T) = \frac{2hv^3}{c(e^{hv/k_BT}-1)}$$
इस समय के दौरान, अत्यधिक लगातार बातचीत के कारण, फोटॉनों का औसत मुक्त मार्ग बहुत छोटा था। ब्रह्मांड विकिरण के लिए अपारदर्शी था। प्रारंभिक ब्रह्मांड विकिरण का प्रभुत्व था। ब्रह्मांड इस तरह विकसित हुआ कि पदार्थ और विकिरण थर्मल इक्विलिब्रियम तक पहुंच गए और उनका ऊर्जा घनत्व बराबर हो गया। इसे स्केल फैक्टर के साथ घनत्व के विकास को दर्शाने वाले ग्राफ से देखा जा सकता है। आइए हम स्केल फैक्टर (समय) (a) (t) का पता लगाते हैं, जिस पर पदार्थ और विकिरण संतुलन में पहुंच गए।
$$\rho_m \propto \frac{1}{a^3}, \: \rho_r \propto \frac{1}{a^4}$$
$$\frac{\rho_{m,t}}{\rho_{r,t}} = \frac{\Omega_{m,t}}{\Omega_{r,t}} = \frac{\Omega_{m,0}}{\Omega_{r,0}}a(t)$$
संतुलन पर,
$$\frac{\rho_{m,t}}{\rho_{r,t}} = \frac{\Omega_{m,t}}{\Omega_{r,t}} = 1$$
$$\Rightarrow \frac{\Omega_{m,0}}{\Omega_{r,0}}a(t) = 1 \: \Rightarrow a(t) = 2.96 \times 10^{-4}$$
का उपयोग करते हुए $\Omega_{m,0} = 0.27$ तथा $\Omega_{r,0} = 8 \times 10^{−5}$। इस स्केल फैक्टर के अनुसार लाल पारी किसके द्वारा दी गई है -
$$z = 1/a(t)-1 \approx 3375$$
ब्रह्मांड के विस्तार के कारण विकिरण का ऊर्जा घनत्व कम हो गया। इस प्रकार ब्रह्मांड ठंडा होने लगा। जैसे-जैसे फोटोन की ऊर्जा कम होने लगी, तटस्थ परमाणु बनने लगे। इस प्रकार, 1300 के एक रेडशिफ्ट के आसपास, तटस्थ हाइड्रोजन बनना शुरू हो गया। इस युग का तापमान 3000K के करीब था।
पदार्थ और विकिरण के बीच की बातचीत बहुत ही असंगत हो गई और इस तरह ब्रह्मांड विकिरण के लिए पारदर्शी होने लगा। इस समयावधि को कहते हैं“Surface of last scattering”चूंकि फोटॉनों का औसत मुक्त मार्ग बहुत बड़ा हो गया था जिसके कारण इस अवधि के बाद शायद ही कोई बिखराव हुआ। इसे भी कहा जाता है“Cosmic Photosphere”।
याद दिलाने के संकेत
CMB उस समय के फोटॉनों द्वारा गठित किया जाता है जब पदार्थ और विकिरण संतुलन में थे।
प्रारंभिक ब्रह्मांड बहुत गर्म था और पदार्थ के तटस्थ रहने के लिए ऊर्जा बहुत अधिक थी, इसलिए यह आयनित पदार्थ-प्लाज्मा के रूप में मौजूद था।
कॉम्पटन स्कैटरिंग, थॉमसन स्कैटरिंग, इनवर्सन कॉम्पटन स्कैटरिंग तब 3 पदार्थ-विकिरण संपर्क प्रक्रियाएं थीं।
ब्रह्माण्ड ऐसे विकसित हुए कि द्रव्य और विकिरण थर्मल संतुलन में पहुँच गए।
हमें पहले यह समझना चाहिए कि क्या विशेषता है decoupling। हम जानते हैं कि ऊर्जाएँ इस हद तक बहुत अधिक थीं कि केवल पदार्थ के रूप में ही अस्तित्व में थीIonized Particles। इस प्रकार, decoupling और पुनर्संयोजन युगों में, हाइड्रोजन के आयनीकरण की अनुमति देने के लिए ऊर्जा को छोड़ना पड़ा। डिकॉउलिंग के समय तापमान के अनुमान से अनुमानित गणना की जा सकती है।
यह इस प्रकार किया गया है -
सबसे पहले, ग्राउंड स्टेट हाइड्रोजन के केवल आयनीकरण पर विचार करें।
$$hv \approx k_BT$$
$$\therefore T \approx \frac{hv}{k_B}$$
जमीन राज्य हाइड्रोजन के आयनीकरण के लिए, hν 13.6 eV है और kB है Boltzmann Constant8.61 × 10 e5 eV / K जो तापमान को 1.5 × 105 केल्विन होने का खुलासा करता है।
यह अनिवार्य रूप से हमें बताता है कि यदि तापमान 1.5 × 10 5 K से नीचे है , तो तटस्थ परमाणु बनने शुरू हो सकते हैं।
हम जानते हैं कि बैरियों के लिए फोटॉन का अनुपात लगभग 5 × 10 10 है । इसलिए ग्राफ की पूंछ पर भी जहां फोटोन की संख्या कम हो जाती है, वहां हाइड्रोजन परमाणुओं को आयनित करने के लिए पर्याप्त फोटॉन होंगे। इसके अलावा, इलेक्ट्रॉन और प्रोटॉन का पुनर्संयोजन एक जमीनी राज्य हाइड्रोजन परमाणु की गारंटी नहीं देता है। उत्तेजित राज्यों को आयनीकरण के लिए कम ऊर्जा की आवश्यकता होती है। इसलिए एक सटीक मूल्य प्राप्त करने के लिए एक अनुशासित सांख्यिकीय विश्लेषण मामले के आधार पर किया जाना चाहिए। अभिकलन तापमान 3000K के आसपास होना तय करते हैं।
स्पष्टीकरण के लिए, हम पहले उत्तेजित अवस्था में रोमांचक हाइड्रोजन के मामले पर विचार करते हैं। से अधिक ऊर्जा वाले फोटॉनों की संख्या के अनुपात के लिए सामान्य अभिव्यक्तिΔE, Nγ (> ΔE) फोटॉनों की कुल संख्या के लिए Nγ द्वारा दिया गया है -
$$\frac{N_\gamma(> \Delta E)}{N_\gamma} \propto e^{\frac{-\Delta E}{kT}}$$
पहले उत्साहित राज्य के लिए रोमांचक हाइड्रोजन के मामले के लिए, ΔE10.2 eV है। अब, यदि हम प्रत्येक बैरियोन के लिए 10.2 से अधिक ऊर्जा के साथ कम से कम 1 फोटॉन की अत्यधिक रूढ़िवादी संख्या पर विचार करते हैं (यह ध्यान में रखते हुए कि अनुपात 5 × 10 10 है , तो हम समीकरण 3 से 4800 K (Inserted γ) के रूप में तापमान प्राप्त करते हैं। NE) = एनपी)।
यह पहला उत्तेजित अवस्था में तटस्थ हाइड्रोजन परमाणुओं की आबादी बनाने का तापमान है। इसे आयनित करने का तापमान काफी कम है। इस प्रकार, हम 1.5 × 10 5 K से बेहतर अनुमान प्राप्त करते हैं जो 3000 K के स्वीकृत मूल्य के करीब है।
रेडशिफ्ट - तापमान संबंध
रेडशिफ्ट और तापमान के बीच संबंध को समझने के लिए, हम नीचे वर्णित दो विधियों को नियोजित करते हैं।
विधि 1
से Wien’s Law, हम जानते हैं कि
$$\lambda_mT = constant$$
इसे रेडशिफ्ट से संबंधित करने के लिए, हम उपयोग करते हैं -
$$1+z = \frac{\lambda_0}{\lambda_e}$$
जैसा $λ_oT_o = λ_eT(z)$, हमें मिलता है -
$$T(z) = T_0\frac{\lambda_0}{\lambda_e} = T_0(1+z)$$
स्थापना To वर्तमान मूल्य 3K के रूप में, हम किसी दिए गए रिडफ़्ट के लिए तापमान मान प्राप्त कर सकते हैं।
विधि 2
आवृत्ति के संदर्भ में, हम जानते हैं -
$$v_0 = \frac{v_e}{1+z}$$
$$B_vdv = \frac{2hv^3}{c^2} \frac{dv}{e^{hv/kT}-1}$$
यह हमें एक ऊर्जा अंतराल के लिए फोटॉन की शुद्ध ऊर्जा के बारे में बताता है और hνएक एकल फोटॉन की ऊर्जा है। इसलिए, हम फोटॉन की संख्या प्राप्त कर सकते हैंBνdν/hν।
अगर $n_{νo}$ वर्तमान और के लिए है $n_{νe}$ उत्सर्जित करने के लिए, हम प्राप्त करते हैं -
$$\frac{n_{v_e}}{n_{v_0}} = (1+z)^3$$
सरलीकरण पर, हम प्राप्त करते हैं,
$$n_{v_0} =\frac{2v_c^2}{c^2}\frac{dv_c}{e^{hv/kT}-1}\frac{1}{(1+z)^3}=\frac{2v_0^2}{c^2}\frac{dv_c}{e^{hv/kT}-1}$$
यह हमें देता है Wien’s Law फिर से और इस तरह यह निष्कर्ष निकाला जा सकता है कि -
$$T(z) = T_0\frac{\lambda_0}{\lambda_e} = T_0(1+z)$$
याद दिलाने के संकेत
- प्रारंभिक ब्रह्मांड बहुत गर्म था, hot 3000K।
- वर्तमान मापों से ब्रह्मांड का तापमान 3K के करीब होने का पता चलता है।
- आगे हम वापस समय में जाते हैं, तापमान आनुपातिक रूप से बढ़ जाता है।
इस अध्याय में, हम CMB विकिरण और COBE के ऐसोट्रॉपी पर चर्चा करेंगे, अर्थात, कॉस्मिक बैकग्राउंड एक्सप्लोरर।
CMB में प्राथमिक Anisotropies
कॉस्मिक माइक्रोवेव बैकग्राउंड रेडिएशन में अंतरिक्ष और प्राथमिक अनिसोट्रोपियों से टिप्पणियों को समझने के लिए, हम निम्नलिखित समीकरणों को लेते हैं और इसे नीचे दिखाए गए अनुसार समझते हैं।
सीएमबी फोटॉन संख्या घनत्व (एन D , 0)
$$n_{\gamma,0} = \frac{Total \: energy \: density}{Characteristic \: energy \:of \:Photons}$$
$$n_{\gamma,0} = \frac{aT_0^4}{k_BT_0}$$
कहाँ पे $k_B$ है Boltzmann Constant तथा $T_0$ है present temperature of the universe।
वर्तमान तापमान का उपयोग करना $(T_0)$2.7 K के रूप में, हमें वर्तमान CMB फोटॉन संख्या घनत्व 400 सेमी −3 के रूप में मिलता है ।
ब्रह्मांडीय तारकीय फोटॉन संख्या घनत्व बड़े पैमानों पर बहुत छोटा (− = 10 −3 सेमी ) 3 ) होता है।
बेरोन से फोटॉन अनुपात (on)
यदि सीएमबी के साथ मिश्रित होने वाली आकाशगंगाओं में तारकीय योगदान नगण्य है, तो प्रोटिओन अनुपात के लिए बेरियन
$$\eta = \frac{n_{b,0}}{n_{\gamma,0}}$$
वर्तमान मूल्य 105 × 10 value10 है । चूँकि फोटॉन और बैरियन संख्या घनत्व दोनों आनुपातिक हैंa−3, फिर η समय के साथ विकसित नहीं होता है।
ऊर्जा घनत्व
संख्या घनत्व के विपरीत, वर्तमान में फोटॉन ऊर्जा घनत्व की तुलना में पदार्थ ऊर्जा घनत्व अधिक हावी है।
बैरोनिक पदार्थ का ऊर्जा घनत्व = $\rho_{b,0}c^2 = 0.04\rho_cc^2 = 2 × 10^{−9} ergcm^{−3}$। जबकि, विकिरण का ऊर्जा घनत्व =$aT_0^4 = 4 \times 10^{−13}ergcm{−3}$।
सीएमबी विकिरण का आइसोट्रॉफी
Penzias तथा Wilsonसीएमबी को टिप्पणियों की सीमा के भीतर आइसोट्रोपिक पाया गया। सीमा कम कोणीय संकल्प और उपकरणों की संवेदनशीलता है। उन्होंने पृथ्वी से अवलोकन किया, इस वजह से, सभी स्पेक्ट्रम के माध्यम से अवलोकन नहीं किया जा सकता है क्योंकि वायुमंडल में जल वाष्प 1 मिमी से 1 मीटर तक कई तरंग दैर्ध्य को अवशोषित करता है। इसलिए, CMB को एक स्पेक्ट्रम के रूप में नहीं माना जा सकता है।
CMB को घूर्णी रूप से अपरिवर्तनीय (आइसोट्रोपिक) माना जाता है। चूंकि एक समय था जब पदार्थ और विकिरण संतुलन में थे, तब ब्रह्मांड में संरचनाओं का गठन अस्पष्ट है। चूंकि पदार्थ का वितरण आइसोट्रोपिक नहीं है, लेकिन एक साथ एक ब्रह्मांडीय वेब की तरह एक साथ टकराया जाता है, बीच में विशाल voids के साथ, CMB को एक एक्सट्रैगैलेटिक मूल माना जाता है।
लेकिन, जैसे ही अंतरिक्ष से अवलोकन शुरू हुआ, सीएमबी में एनोटोट्रोपिस पाए गए, जो इस तर्क को आगे बढ़ाते हैं कि ये एआईएसोट्रोपियां मामले में संरचनाओं के गठन की ओर ले जाती हैं।
अंतरिक्ष से सीएमबी विकिरण का अवलोकन
CMB को देखने के लिए लॉन्च किए गए मुख्य उपग्रह थे -
Cosmic Microwave Background Explorer (COBE, 1989)
Wilkinson Microwave Anisotropy Probe (WMAP, 2001) और
Planck (2009)।
COBE (लौकिक पृष्ठभूमि एक्सप्लोरर)
COBE में मुख्य रूप से दो उपकरण थे। वो थेFar InfraRed Absolute Spectrometer (FIRAS) और Differential Microwave Radiometers(DMR एंटेना)। FIRAS CMB की तीव्रता को किसी विशिष्ट दिशा के साथ तरंग दैर्ध्य के कार्य के रूप में मापता है। जबकि, DMR में तीन अलग-अलग दिशाओं से CMB की तीव्रता के अंतर को मापने के लिए 3 एंटेना हैं। निम्नलिखित संकेत हमें FIRAS और DMR के बारे में कुछ और जानकारी देते हैं।
एफआईएमएएस से सीएमबी टिप्पणियों से पता चलता है कि सीएमबी विकिरण टी = 2.72528। 0.00065 एम पर काले शरीर स्पेक्ट्रम से मेल खाती है।
डीएमआर आकाश में सभी दिशाओं में तीन आवृत्तियों (31.5 गीगाहर्ट्ज, 53 गीगाहर्ट्ज, 90 गीगाहर्ट्ज) को मापता है।
DMR टिप्पणियों में "लाल बैटमैन प्रतीक" अग्रभूमि उत्सर्जन (गैलेक्टिक विसरित सिंक्रोट्रॉन उत्सर्जन) से शोर है।
अवलोकनों में तीव्रता भिन्नता तापमान विविधताओं के अनुरूप है। गर्म और ठंडे स्थानों की उपस्थिति साबित करती है कि सीएमबी विकिरण अनिसोट्रोपिक है।
यह अनिसोट्रॉपी डीकंप्लिंग समय पर मौजूद होना चाहिए क्योंकि सीएमबी में कोई विकृतियां नहीं हैं। इसलिए, द्रव्य में अन्य की तुलना में अधिक घनत्व वाले कुछ पॉकेट होने चाहिए।
COBE परिणाम
CMB स्पेक्ट्रम (ऊर्जा के एक कार्य के रूप में तीव्रता) लगभग एक पूर्ण काला शरीर है जो T = 2.7 K के अनुरूप है। CMB विकिरण की विशिष्ट तीव्रता लगभग सभी दिशाओं के लिए समान है। पुष्टि है कि ब्रह्मांड बड़े पैमाने पर आइसोट्रोपिक है (ब्रह्माण्ड संबंधी सिद्धांत की हमारी धारणा को मान्य करता है)।
डेटा के विश्लेषण से पता चला है कि COBE (DMR) के रिज़ॉल्यूशन में CMB स्पेक्ट्रम में तापमान अनिसोट्रॉपी ("उतार-चढ़ाव") हैं।
Resolution of COBE, WMAP, Planck
डीएमआर उपकरण ऑन-बोर्ड COBE में degrees 7 डिग्री का सीमित (अधिकतम) स्थानिक संकल्प था।
विल्किंसन माइक्रोवेव अनिसोट्रॉपी जांच (WMAP) का औसत रिज़ॉल्यूशन Mic 0.7 डिग्री था।
प्लैंक उपग्रह में minute 10 चाप-मिनट का कोणीय संकल्प है।
याद दिलाने के संकेत
कॉस्मिक स्टेलर फोटॉन संख्या घनत्व CMB फोटॉन संख्या घनत्व की तुलना में बहुत छोटा है।
हम एक मामले में प्रभुत्व वाले ब्रह्मांड में रहते हैं, क्योंकि पदार्थ ऊर्जा घनत्व फोटॉन ऊर्जा घनत्व से अधिक है।
सीबीई, डब्ल्यूएमएपी, प्लैंक सीएमबी में अनिसोट्रोपियों को मापने और निर्धारित करने के प्रयास हैं।
ब्रह्मांड में संरचना का गठन सीएमबी अनिसोट्रोपियों का एक परिणाम है।
जब हम सभी आकाश CMB नक्शे को परिष्कृत, दुरुस्त करते हुए देखते हैं, तो अग्रभूमि संदूषण होता है, जो एक प्रकार का है anisotropyइन मानचित्रों में। हम देख सकते हैं कि ये अग्रभूमि उत्सर्जन आकाशगंगा के दूधिया रास्ते से हैं। सीएमबी की तीव्रता गैलेक्टिक विमान के विमान के साथ अधिक है और जैसे ही हम दूर जाते हैं तीव्रता में कमी आती है। इनमें, हम द्वितीयक विसंगतियों का निरीक्षण कर सकते हैं, जो आकाशगंगा से सिंक्रोट्रॉन उत्सर्जन हैं। ये उत्सर्जन अग्रभूमि संदूषण को बनाते हैं। आकाश से सीएमबी उत्सर्जन को देखने के लिए, हमें इन अग्रभूमि उत्सर्जन को घटाना होगा।
निम्न छवि सीएमबी को अग्रभूमि उत्सर्जन के साथ दिखाती है।

डिपोल अनिसोट्रॉपी
एक अन्य प्रकार का अनिसोट्रॉपी है, जो सीएमबी सभी आकाश मानचित्र में पाया गया था, इसे डिपोल अनिसोप्रोपी कहा जाता है। यह प्रारंभिक ब्रह्मांड से जुड़ा नहीं है। इसे गोलाकार हार्मोनिक कार्यों का उपयोग करके दिखाया जा सकता है। यदि गोलाकार सतह पर एक पैटर्न है और हम गणितीय कार्यों का उपयोग करके इसे मैप करना चाहते हैं, तो हम त्रिकोणमितीय कार्यों का उपयोग करके ऐसा कर सकते हैं। इसलिए, जब हम मैप करते हैं, तो यह एक मोनोपोल हो सकता है - हर दिशा में एक ही, या एक द्विध्रुवीय - गुण जब 180 डिग्री पर घुमाया जाता है। इसी तरह, हमारे पास चौगुना है और इसी तरह। एक जटिल पैटर्न के लिए, इसे इन मोनोपोल, द्विध्रुवीय, चौगुनी आदि के योग के रूप में व्यक्त किया जा सकता है।
सीएमबी को इस तरह से तैयार किया जाता है कि सभी आकाश मानचित्रों में अनिसोट्रॉपी के प्रमुख स्रोतों में से एक यह द्विध्रुवीय एनिसोट्रॉपी है, लेकिन यह सीएमबी का मौलिक आदर्श नहीं है। यह नीचे दी गई छवि में देखा जा सकता है।

जो द्विध्रुवीय दिशा हमें देखने को मिलती है वह कोई यादृच्छिक दिशा नहीं है। डिपोल अनिसोट्रॉपी की एक दिशा होती है। हम सीएमबी की तीव्रता को एक विशिष्ट दिशा के साथ देखते हैं। यह दिशा सौर मंडल के वेग वेक्टर के कारण है। पृथ्वी के वेग को सूर्य या आकाशगंगा के केंद्र के संबंध में दर्शाया जा सकता है। जिस दिशा में पृथ्वी घूम रही है, हम एक ब्लूशिफ्ट और रेडशिफ्ट का निरीक्षण करते हैं और द्विध्रुव इस दिशा में स्थित है।
उपरोक्त छवि में एक विशिष्ट द्विध्रुवीय उपस्थिति है क्योंकि हमारी गैलेक्सी एक विशिष्ट दिशा में घूम रही है। परिणाम है - आकाश का एक पक्ष Redshifted दिखाई देगा और आकाश का दूसरा भाग Blueshifted दिखाई देगा। इस मामले में, Redshifting का मतलब है कि फोटॉन तरंग दैर्ध्य = कूलर में हैं (इसलिए उनके नाम से पीछे की ओर, वे ऊपर के आरेख में नीले दिखते हैं)।
हम कह सकते हैं, पृथ्वी एक निश्चित समय पर आकाश में सूरज / गांगेय केंद्र / सीएमबी के संबंध में कुछ विशिष्ट दिशा में आगे बढ़ रही है। फिर, यदि हम किसी भी कोण को देखते हैं और सीएमबी के लिए तापमान को मापते हैं, तो यह अलग होगा। ऐसा इसलिए है, क्योंकि हम फोटॉनों को माप रहे हैं जो या तो ब्लूशिफ्टेड या रेडशिफ्टेड हैं और यह आकाश में फोटॉन की दृष्टि की रेखा पर निर्भर करता है।
याद दिलाने के संकेत
सीएमबी सभी आकाश मानचित्र में अग्रभूमि संदूषण को सीएमबी का अनिसोट्रॉपी कहा जाता है।
ये उत्सर्जन हमारी अपनी दूधिया आकाशगंगा से होते हैं।
2 प्रकार की अनिसोट्रोपियां हैं: डिपोल एनिसोट्रॉपी और कोणीय पावर स्पेक्ट्रम एनिसोट्रॉपी।
डिपोल अनिसोट्रॉपी एक विशिष्ट दिशा में है, जबकि कोणीय पावर स्पेक्ट्रम एनिसोट्रॉफी हर जगह फैली हुई है।
क्षितिज की लंबाई 'द बिग बैंग' से 'द रिकॉम्बिनेशन एरा' तक प्रकाश फोटोज द्वारा तय की गई दूरी है। कोणीय स्पेक्ट्रम का 1 सेंट शिखर ◦ = 1 l (l = 180) पर है, जो एक बहुत ही विशेष लंबाई का पैमाना है।
दो बिंदुओं के बीच उचित दूरी किसके द्वारा दी गई है -
$$r_p = \int_{0}^{t}cdt$$
जब हम t = 0 से t = t rec का टाइम फ्रेम लेते हैं , तब
$$r_H = \int_{0}^{t_{rec}}cdt$$
कहाँ पे $r_H$ उचित क्षितिज दूरी है।
अब, हम जानते हैं कि -
$$\dot{a} = \frac{\mathrm{d} a}{\mathrm{d} t}$$
$$dt = \frac{da}{\dot{a}}$$
जब t = 0, a = 0।
फिर $t = t_{rec}, a = a_0 / (1 + z_{rec})$।
इसलिए, हम लिख सकते हैं,
$$r_H(z_{rec})=\int_{0}^{a_{rec}} c\frac{da}{aH}$$
$$H(a_{rec}) = H(z_{rec}) = H_0\sqrt{\Omega_{m,0}}a^{-3/2}$$
दौरान Recombination period universeबात हावी थी। अर्थात,Ωrad << Ωmatter। इसलिए, विकिरण शब्द को गिरा दिया जाता है।
$$r_H(z_{rec}) = \frac{c}{H_0\sqrt{\Omega_{m,0}}}\int_{0}^{a_{rec}} \frac{da}{a^{-1/2}}$$
$$r_H(z_{rec}) = \frac{2c}{3H_0\sqrt{\Omega_{m,0}}}\frac{1}{(1+z_{rec})^{3/2}}$$
$$\theta_H(rec) = \frac{r_H(z_{rec})}{d_A(z_{rec})}$$
जो 0.5 डिग्री के बराबर है, अगर हम समीकरण में सभी ज्ञात मान रखते हैं।
Electromagnetic radiationपिछले बिखरने की सतह से अपारदर्शी है। एक-दूसरे के क्षितिज के भीतर स्थित किसी भी दो बिंदु 'नहीं' के समान गुण नहीं हैं। तो, यह विभिन्न तापमान मान देगा।
हम इस धरातल पर दो बिंदु प्राप्त कर सकते हैं जो एक दूसरे के साथ नहीं मिलते हैं, जिसका अर्थ है कि एक बिंदु पर ब्रह्मांड प्रकाश की गति से अधिक तेजी से विस्तारित होता है जो विस्तार के लिए मुद्रास्फीति मॉडल है।
याद दिलाने के संकेत
क्षितिज की लंबाई 'द बिग बैंग' से 'द रिकॉम्बिनेशन एरा' तक प्रकाश फोटोज द्वारा तय की गई दूरी है।
पुनर्संयोजन अवधि के दौरान, ब्रह्मांड का बोलबाला था।
विद्युत चुम्बकीय विकिरण अंतिम बिखरने की सतह से अपारदर्शी है।
Astrobiologyब्रह्मांड में उत्पत्ति, विकास, वितरण और भविष्य के भविष्य का अध्ययन है। इसका संबंध खोज और पता लगाने से हैExtrasolar Planets।
Astrobiology निम्नलिखित बिंदुओं को संबोधित करता है -
जीवन कैसे शुरू और विकसित होता है? (जीव विज्ञान + भूविज्ञान + रसायन विज्ञान + वायुमंडलीय विज्ञान)
क्या पृथ्वी से परे ऐसी दुनियाएँ हैं जो जीवन के लिए अनुकूल हैं? (खगोल विज्ञान)
पृथ्वी पर जीवन का भविष्य क्या होगा?
Astronomy निम्नलिखित बिंदुओं को संबोधित करता है -
अन्य तारों के चारों ओर ग्रह प्रणाली का पता कैसे लगाया जाए?
विधि में से एक प्रत्यक्ष इमेजिंग है, लेकिन यह एक बहुत ही मुश्किल काम है क्योंकि ग्रह सितारों की तुलना में बेहद फीके प्रकाश स्रोत हैं, और जो थोड़ा प्रकाश उनसे आता है वह अपने मूल तारे से चकाचौंध में खो जाता है।
जब ग्रह अपने मूल तारे और गर्म के करीब होता है, तो कंट्रास्ट बेहतर होता है, ताकि वह तीव्र अवरक्त विकिरण का उत्सर्जन करे। हम अवरक्त क्षेत्र में चित्र बना सकते हैं।
एक्स्ट्रासोलर प्लेनेट डिटेक्शन की तकनीक
एक्स्ट्रासोलर ग्रह का पता लगाने की सबसे कुशल तकनीकें इस प्रकार हैं। इनमें से प्रत्येक को बाद के अध्यायों में भी विस्तार से बताया गया है।
रेडियल वेलोसिटी विधि
इसे डॉपलर विधि भी कहा जाता है। इसमें -
स्टार ग्रह प्रणाली अपने बायर्सेंटर, स्टार वॉबल्स के चारों ओर घूमती है।
Wobbling द्वारा पता लगाया जा सकता है
समय-समय पर लाल / नीली पाली। एस्ट्रोमेट्री - आकाश में वस्तुओं को बहुत सटीक रूप से मापना।
पारगमन विधि
ट्रांज़िट मेथड (केप्लर स्पेस टेलीस्कोप) का उपयोग आकार ज्ञात करने के लिए किया जाता है। एक द्विआधारी प्रणाली के विपरीत, ग्रह द्वारा तारा की चमक में डुबकी आमतौर पर बहुत कम होती है।
प्रत्यक्ष इमेजिंग
एक दूरबीन का उपयोग करके ग्रह का इमेजिंग।
आइए हम रेडियल वेलोसिटी मेथड पर किए गए एक केस स्टडी को देखें।
मामले का अध्ययन
यह केस स्टडी सर्कुलर ऑर्बिट पर है और ऑर्बिट की प्लेन की परिक्रमा आकाश के प्लेन पर है। बैरीकेटर के चारों ओर लगने वाला समय समान होगा। यह दो रेडशिफ्ट या ब्लूशिफ्ट के बीच के समय के अंतर के बराबर होगा।
निम्नलिखित छवि पर विचार करें।

ए और सी पर - पूर्ण वेग मापा जाता है। C पर, वेग शून्य है।
Vrmax = V * तारे का वास्तविक वेग है।
P, तारे के साथ-साथ ग्रह का समय-काल है।
of कक्षा का चरण है।
स्टार मास - एम * , ऑर्बिट रेडियस ए * , प्लैनेट मासmp।
जन समीकरण के केंद्र से,
$$m_p a_p = M_\ast a_\ast$$
वेग के समीकरण से,
$$V_\ast = \frac{2\pi a_\ast}{P}$$
$$\Rightarrow a_\ast = \frac{PV_\ast}{2\pi}$$
से Kepler’s Law,
$$P^2 = \frac{4\pi^2a_p^3}{GM_\ast}$$
$$\Rightarrow a_p = \left ( \frac{P^2GM_\ast}{4\pi^2} \right)^{1/3}$$
उपरोक्त समीकरणों से, हमें मिलता है -
$$\Rightarrow m_p = \left( \frac{P}{2\pi G} \right)^{1/3}M_\ast^{2/3}V_\ast$$
हमें मिला: $m_p, a_p$ तथा $a_\ast$।
उपरोक्त समीकरण सितारे के सबसे बड़े ग्रहों के पक्षपाती हैं।
याद दिलाने के संकेत
ब्रह्मांड में जीवन की उत्पत्ति, विकास, वितरण और भविष्य का अध्ययन खगोल विज्ञान करता है।
एक्स्ट्रासोलर ग्रहों का पता लगाने की तकनीकें हैं: रेडियल वेलोसिटी मेथड, ट्रांजिट मेथड, डायरेक्ट इमेजिंग आदि।
वॉबलिंग का समय-समय पर लाल / नीली शिफ्ट और एस्ट्रोमेट्री द्वारा पता लगाया जा सकता है।
रेडियल वेलोसिटी मेथड में बड़े पैमाने पर तारे के करीब ग्रहों का पता लगाने के लिए पक्षपाती है।
पिछले अध्याय में, रेडियल वेलोसिटी विधि उस मामले के लिए जिसमें कक्षीय विमान और आकाश के विमान लंबवत हैं, परिक्रमा कक्षाओं के लिए चर्चा की गई थी। यहां, हम एक और मामले से निपटते हैं, जब कक्षीय विमान और आकाश के विमान परिपत्र कक्षाओं के लिए लंबवत नहीं होते हैं।
जब कक्षीय समतल आकाश के तल के संबंध में कोण पर होता है (लंबवत नहीं), तो हमारी निम्न स्थिति होती है -

इस मामले में, जब वे लंबवत थे, हमारे पास दो बिंदु थे, जिस पर हम वास्तविक वेग को माप सकते थे। लेकिन यहां, यह संभव नहीं है। सभी बिंदुओं पर, हम केवल वास्तविक वेग के एक घटक को माप सकते हैं,v।
$$v_r = v \:sin(i)cos(\theta)$$
कहाँ पे θकक्षा का वह चरण है जो समय पर निर्भर मात्रा है। झुकाव कोणiदूसरी ओर, समय-स्वतंत्र है। इसलिये,
$$(v_r)_{max} = v\: sin(i)$$
मनाया गया रेडियल वेग वक्र निम्न प्रकार का होगा -

जब कक्षीय तल आकाश के लंबवत होता है -
$$m_p = \left ( \frac{P}{2\pi G} \right )^{\frac{1}{3}}(M_\ast)^{\frac{2}{3}}v$$
कहाँ पे mp, P, G, M∗क्रमशः ग्रह, कक्षीय अवधि, सार्वभौमिक गुरुत्वाकर्षण स्थिरांक और तारे का द्रव्यमान। लेकिन इस मामले में, हमें इसे निम्नानुसार संशोधित करना चाहिए -
$$m_psin(i) = \left ( \frac{P}{2\pi G} \right )^{\frac{1}{3}} (M_\ast)^{\frac{2}{3}}(v_r)_{max}$$
लेकिन, i का मान पाना एक मुश्किल काम है। के मान पर हम कुछ अड़चनें लगा सकते हैंiपारगमन विधि का उपयोग करना। तारे और पृथ्वी के बीच ग्रह के पारित होने को गोचर कहा जाता है। हम एक पारगमन का अवलोकन करके प्रकाश वक्र प्राप्त कर सकते हैं और प्रकाश वक्र के अवलोकन प्रवाह में एक महत्वपूर्ण डुबकी का अर्थ है कि मैं 90 डिग्री के करीब हूं। यदि ऐसी शर्तें पूरी नहीं होती हैं, तो हम मूल्य के बारे में कोई विचार नहीं कर सकते हैंi। तब का मूल्यmp हम पाते हैं कि यह ग्रह के द्रव्यमान के लिए एक निचली सीमा के रूप में काम कर सकता है, क्योंकि यह वास्तव में है mp sin(i) तथा sin(i) ≤ 1।
निष्कर्ष निकालने के लिए, रेडियल वेग विधि पारगमन विधि की तुलना में अधिक सुविधाजनक है क्योंकि रेडियल वेग किसी भी समय मापा जा सकता है लेकिन पारगमन माप केवल पारगमन के दौरान बनाया जा सकता है जो लंबे समय तक नहीं रह सकता है।
याद दिलाने के संकेत
ग्रह की कक्षा का झुकाव रेडियल वेग विधि द्वारा प्राप्त नहीं किया गया है।
रेडियल वेलोसिटी मेथड ट्रांज़िट मेथड से बेहतर है क्योंकि रेडियल वेलोसिटी को हमेशा ट्रांज़िट के विपरीत मापा जा सकता है।
पारगमन अल्पकालिक हैं और बहुत आसानी से छूट जाते हैं।
पारगमन विधि (Kepler Space Telescope)आकार का पता लगाने के लिए उपयोग किया जाता है। एक ग्रह द्वारा एक तारे की चमक में डुबकी आमतौर पर एक बाइनरी सिस्टम के विपरीत बहुत कम होती है।
F0 इससे पहले कि ग्रह इसे दोष देता है, स्टार का प्रवाह है।
F1 संपूर्ण ग्रह तारा के सामने होने के बाद प्रवाह है।
सभी गणनाओं के लिए निम्न छवि का उपयोग किया जाएगा।

$$\frac{F_0 - F_1}{F_0} = \frac{\pi r_p^{2}}{\pi R^2_\ast}$$
$$\frac{\Delta F}{F} \cong \frac{r^2_p}{R^2_\ast}$$
$$\left ( \frac{\Delta F}{F} \right )_{earth} \cong 0.001\%$$
$$\left ( \frac{\Delta F}{F} \right )_{jupiter} \cong 1\%$$
यह जमीन आधारित दूरबीन द्वारा हासिल करना आसान नहीं है। यह हब्बल दूरबीन द्वारा हासिल किया गया है।

यहाँ, $t_T$ ए और डी के बीच का समय है $t_F$ स्थिति B और C के बीच का समय है
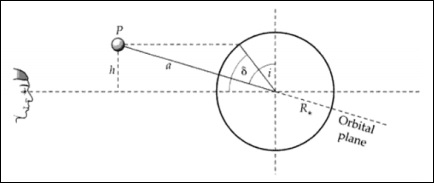
झुकाव से संबंधित एक पारगमन की ज्यामिति iप्रणाली में। पारगमन अक्षांश और झुकाव विनिमेय हैं।
उपरोक्त चित्रों से, हम लिख सकते हैं -
$$\frac{h}{a} = cos(i)$$
$$\frac{h}{R_\ast} = sin(\delta)$$
$$cos(i) = \frac{R_\ast sin(\delta)}{a}$$
$$y^2 = (R_\ast + R_p)^2 - h^2$$
$$y = [(R_\ast + R_p)^2 - h^2]^{\frac{1}{2}}$$
$$sin(\theta) = \frac{y}{a}$$
$$\theta = sin^{-1}\left [ \frac{(R_\ast + R_p)^2 - a^2cos^2(i)}{a^2} \right ]^{\frac{1}{2}}$$
$$t_T = \frac{P}{2\pi} \times 2\theta$$
यहाँ, $t_T$ समयावधि का वह अंश है जिसके लिए पारगमन होता है और (2π / 2 is) कोण का अंश होता है जिसके लिए पारगमन होता है।
$$sin(\frac{t_T\pi}{P}) = \frac{R_\ast}{a}\left [ \left ( 1+ \frac{R_p}{R_\ast}\right )^2 - \left ( \frac{a}{R_\ast}cos(i)\right )^2 \right ]^{\frac{1}{2}}$$
आमतौर पर, एक >> आर ∗ >> आरपी। तो, हम लिख सकते हैं -
$$sin(\frac{t_T\pi}{P}) = \frac{R_\ast}{a}\left [ 1- \left ( \frac{a}{R_\ast}cos(i) \right )^2\right ]^{\frac{1}{2}}$$
यहाँ, Pदो पारगमन के बीच की अवधि है। कक्षीय समयावधि की तुलना में पारगमन का समय बहुत कम है। इसलिये,
$$t_T = \frac{P}{\pi}\left [ \left ( \frac{R_\ast}{a}\right )^2 - cos^2(i)\right ]^{\frac{1}{2}}$$
यहाँ, tT, P, R∗ वेधशालाएं हैं, a तथा i पता लगाना चाहिए।
अभी,
$$sin(\frac{t_F\pi}{P}) = \frac{R_\ast}{a}\left [\left (1 - \frac{R_p}{R_\ast} \right )^2 - \left ( \frac{a}{R_\ast}cos\:i \right )^2\right ]^{\frac{1}{2}}$$
कहाँ पे, $y^2 = (R_\ast − R_p)^2 − h^2$।
चलो,
$$\frac{\Delta F}{F} = D = \left ( \frac{R_p}{R_\ast} \right )^2$$
अब, हम व्यक्त कर सकते हैं,
$$\frac{a}{R_\ast} = \frac{2P}{\pi} D^{\frac{1}{4}}(t^2_T - t^2_F)^{-\frac{1}{2}}$$
मुख्य अनुक्रम सितारों के लिए,
$$R_\ast \propto M^\alpha_\ast$$
$$\frac{R_\ast}{R_0} \propto \left ( \frac{M_\ast}{M_0}\right )^\alpha$$
यह देता है R∗।
इसलिए, हमें 'a' का भी मान मिलता है।
तो, हमें 'आर पी ', 'एप' और यहां तक कि 'आई' मिलता है।
इस सब के लिए,
$$h \leq R_\ast + R_p$$
$$a\: cos\: i \leq R_\ast + R_p$$
~ 89 डिग्री के लिए भी, पारगमन की अवधि बहुत छोटी है। पर्याप्त पारगमन समय प्राप्त करने के लिए ग्रह को बहुत करीब होना चाहिए। यह 'i' पर एक तंग बाधा देता है। एक बार जब हम 'i' प्राप्त कर लेते हैं, तो हम 'm p ' को रेडियल वेग माप से प्राप्त कर सकते हैं ।
पारगमन विधि द्वारा इस पता लगाने को मौका का पता लगाने के रूप में कहा जाता है, अर्थात, पारगमन देखने की संभावना। पारगमन संभावना (अवलोकन की संभावना) गणना नीचे दिखाई गई है।
पारगमन की संभावना दो चरम पारगमन विन्यासों द्वारा पता लगाए गए ठोस कोण से संबंधित है, जो है -
$$Solid \: angle \:of \:planet \: = 2\pi \left ( \frac{2R_\ast}{a} \right )$$
साथ ही एक अर्ध-प्रमुख अक्ष पर कुल ठोस कोण a, या -
$$Solid \:angle \:of \:sphere \: =\: 4\pi$$
संभावना इन दोनों क्षेत्रों का अनुपात है -
$$= \: \frac{area \:of\: sky \: covered \:by\: favourable \: orientation}{area\: of\: sky \:covered\: by\: all\: possible\: orientation\: of\: orbit}$$
$= \frac{4\pi a_pR_\ast}{4\pi a^2_p} = \frac{R_\ast}{a_p}$ $\frac{area\: of\: hollow \: cyclinder}{area\: of\: sphere}$
यह संभावना प्रेक्षक से स्वतंत्र है।
याद दिलाने के संकेत
- ट्रांज़िट मेथड (केप्लर स्पेस टेलीस्कोप) का उपयोग आकार ज्ञात करने के लिए किया जाता है।
- ट्रांजिट विधि द्वारा जांच एक मौका का पता लगाने है।
- पर्याप्त पारगमन समय प्राप्त करने के लिए ग्रह को बहुत करीब होना चाहिए।
- पारगमन संभावना ग्रह के ठोस कोण से संबंधित है।
- यह संभावना संदर्भ के पर्यवेक्षक फ्रेम से स्वतंत्र है।
2004 में एक एक्स्ट्रासोलर ग्रह की पहली प्रत्यक्ष छवि, बड़े पैमाने पर एक ग्रह की थी 3-10 Mjupiter एक द्रव्यमान के साथ एक भूरे रंग के बौने (2M1207) की परिक्रमा 25 Mjupiter। एक्सोप्लैनेट्स का पता लगाने के लिए रेडियल वेलोसिटी, ट्रांजिट, ग्रेविटेशनल माइक्रोलेंसिंग, इमेजिंग, एस्ट्रोमेट्री आदि तकनीकों का इस्तेमाल किया गया है। हर साल बंदियों की संख्या बढ़ रही है।
2010 के आसपास तक, रेडियल वेग विधि का बड़े पैमाने पर उपयोग किया गया था, लेकिन अब अधिकांश डिटेक्शन ट्रांजिट विधि द्वारा किए जाते हैं। 2014 में हिरासत की संख्या में स्पाइक था, जो तब थाKepler Space Telescope (KST) परिणाम देने लगे।
एक मास-पीरियड डिस्ट्रीब्यूशन से पता चलता है कि रेडियल वेलोसिटी मेथड एक बड़े पीरियड के साथ बड़े ग्रहों का पता लगाने के लिए अधिक पक्षपाती है, जबकि ट्रांज़िट पद्धति का उपयोग करते हुए, कम अवधि वाले ग्रहों को केवल निम्न छवि में दिखाया गया है (सौजन्य: NASA सोप्लैनेट आर्काइव) ।
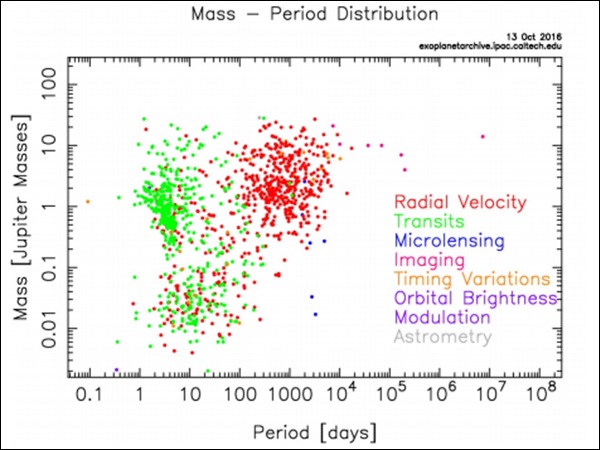
केएसटी के आगमन के बाद से छोटे बड़े ग्रहों का पता लगाने की संख्या में भारी वृद्धि हुई है। यह नीचे दिए गए आंकड़े से स्पष्ट है। केएसटी द्वारा पाए गए ग्रहों को दो समूहों में विभाजित किया गया है: गर्म बड़े ग्रह जिन्हें "हॉट जुपिटर" और निचले द्रव्यमान ग्रहों को "हॉट सुपर अर्थ" कहा जाता है (क्योंकि वे पृथ्वी से अधिक विशाल हैं)।

जब हम एक्सट्रासोलर ग्रहों की संख्या का पता लगाते हैं, तो उनसे दूरी के आधार पर, हम पाते हैं कि इनमें से अधिकांश ग्रह 2kpc के भीतर हैं, जो हमारी आकाशगंगा के भीतर अच्छी तरह से है। शायद ब्रह्मांड में ग्रह इतने असामान्य नहीं हैं, क्योंकि हमारी खोज ब्रह्मांड के बहुत कम हिस्से में केवल कुछ विशेष प्रकार के ग्रहों तक ही सीमित है।
से ग्रह बनते हैं circumstellar disc या proto planetary disc। यदि तारा निर्माण के दौरान ग्रहों को उप-उत्पाद के रूप में बनाया जाता है, तो शायद ब्रह्मांड में संख्या ग्रह ब्रह्मांड में सितारों की संख्या से अधिक है !!
रहने योग्य क्षेत्र
हैबिटेबल ज़ोन को तारे के आसपास के ज़ोन के रूप में परिभाषित किया जा सकता है जहाँ पानी अपने तरल रूप में मौजूद हो सकता है। दूरी पर एक ग्रह पर विचार करें$a_p$निम्न आकृति में दिखाए गए तारे से। ग्रह के तापमान की गणना के लिए एक सरल विधि इस प्रकार वर्णित है।
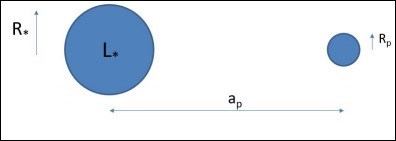
$$\left ( \frac{L_\ast}{4\pi a^2_p} \right )\pi R^2_p(1 - A) = 4\pi R^2_p \sigma T^4_p$$
तथा
$$\frac{L_\ast}{4\pi R^2_\ast} = \sigma T^4_\ast$$
$$\therefore T_p = (1 - A)T_\ast \sqrt{\frac{R_\ast}{2a_p}}$$
हमारे मामले में प्रतिस्थापन
Lsun = 3.83 x 1026
ap = 1.5 ∗ 1011 and
A = 0.3
दे देंगे $T_{Earth} = 255K$। वास्तविक गणना बहुत शामिल है जिसमें क्लाउड भौतिकी शामिल है। हमारे सौर मंडल में रहने योग्य क्षेत्र 0.9 एयू और 1.7 एयू के बीच स्थित है।
घटते गैस के दबाव के कारण सूर्य का प्रकाश समय के साथ बढ़ता हुआ पाया गया। हाइड्रोजन जलाने के समय यह 30% कम चमकीला था। इसका परिणाम सूर्य से दूर रहने योग्य क्षेत्र में बदलाव होगा। चूँकि पृथ्वी हेबिटेबल ज़ोन के अंदरूनी किनारे के पास है, शायद एक दिन यह ज़ोन से बाहर निकल जाएगा!
लगातार रहने योग्य क्षेत्र
संक्षेप में इसे ही कहा जाता है CHZउस क्षेत्र के रूप में परिभाषित किया जा सकता है जिसमें तरल पानी एक तारे के पूरे मुख्य क्रम पर आ सकता है। केएसटी ने कई एक्स्ट्रासोलर ग्रहों का पता लगाया है जो निवास योग्य क्षेत्र में स्थित हैं।
एक जैव-हस्ताक्षर किसी भी पदार्थ - जैसे कि एक तत्व, आइसोटोप, अणु या घटना है जो पिछले या वर्तमान जीवन के वैज्ञानिक प्रमाण प्रदान करता है। एक उदाहरण एक ग्रह पर ओ 2 और सीओ 2 दोनों का पता लगा रहा है, जो आमतौर पर अकेले भूवैज्ञानिक प्रक्रियाओं के माध्यम से संभव नहीं है। यह पता अवशोषण स्पेक्ट्रा का विश्लेषण करके किया जाता है।
याद दिलाने के संकेत
एक्सोप्लैनेट्स का पता लगाने के लिए रेडियल वेलोसिटी, ट्रांजिट, ग्रेविटेशनल माइक्रोलेंसिंग, इमेजिंग, एस्ट्रोमेट्री आदि तकनीकों का इस्तेमाल किया गया है।
रेडियल वेलोसिटी विधि बड़े अवधि वाले बड़े ग्रहों का पता लगाने की दिशा में अधिक पक्षपाती है।
गर्म बड़े ग्रहों को "हॉट जुपिटर" और निचले जन ग्रहों को "हॉट सुपर अर्थ" कहा जाता है।
ब्रह्मांड में ग्रहों की संख्या ब्रह्मांड में सितारों की संख्या से अधिक है।
हैबिटेबल ज़ोन को तारे के आसपास के ज़ोन के रूप में परिभाषित किया जा सकता है जहाँ पानी अपने तरल रूप में मौजूद हो सकता है।