कॉस्मोलॉजी - रेडिएशन डॉमिनेटेड यूनिवर्स
इस अध्याय में, हम रेडिएशन डोमिनेटेड यूनिवर्स से संबंधित फ्रीडमैन समीकरणों के समाधानों पर चर्चा करेंगे। शुरुआत में, हम विकिरण के मामले में ऊर्जा घनत्व की तुलना करते हैं। यह हमें यह देखने में सक्षम करेगा कि क्या हमारे ब्रह्मांड का प्रभुत्व है या विकिरण का प्रभुत्व है।
विकिरण का ऊर्जा घनत्व
वर्तमान ब्रह्मांड में प्रचलित विकिरण को तारकीय स्रोतों के लिए बहुत कम जिम्मेदार ठहराया जा सकता है, लेकिन इसका मुख्य कारण अवशेष सीएमबी (कॉस्मिक माइक्रोवेव बैकग्राउंड) है।
विकिरण की ऊर्जा घनत्व, $ \ epsilon _ {\ Gamma, 0} $, निम्नानुसार व्यक्त की जा सकती है -
$$ \ epsilon _ {\ Gamma, 0} = aT_0 ^ 4 $ $
यहाँ, a वह विकिरण स्थिरांक है जिसकी अभिव्यक्ति $ (8 \ pi ^ 5k_B ^ 4) / (15h ^ 3c ^ 2) $ के बराबर है a = 7.5657 × 10−15erg\: cm−3 K−4। तापमान, T0, हम यहाँ पर विचार करते हैं, जो CMB के अनुरूप काले शरीर से मेल खाता है।
परिणामों को प्रतिस्थापित करते हुए, हमारे पास,
$$ \ epsilon _ {\ Gamma, 0} = aT_0 ^ 4 = 4 \ गुना 10 ^ {- 13} erg \: cm ^ {- 3} $ $
पदार्थ का ऊर्जा घनत्व
निम्नलिखित गणनाओं में, हमें एक सपाट ब्रह्मांड और K = 0. के साथ काम करने की धारणा है। हम मामले की ऊर्जा घनत्व को $ \ epsilon = \ rho c ^ 2 $ मानते हैं। हम निम्नलिखित पर विचार करते हैं -
$$ \ rho_ {m, 0} c ^ 2 = 0.3 \ rho_ {c, 0} c ^ 2 = 0.3 \ गुना \ frac {3H_0 ^ 2} {8 \ pi G} \ टाइम्स c ^ 2 $ $
$$ \ rho_ {m, 0} c ^ 2 \ simeq 2 \ 10 बार 10 ^ {- 8} erg \: cm ^ {- 3} $ $
$ $ \ rho_ {b, 0} c ^ 2 = 0.03 \ rho_ {c, 0} c ^ 2 = 0.03 \ गुना \ frac {3H_0 ^ 2} {8 \ pi G} \ टाइम्स c 2 $ $ $
$$ \ rho_ {b, 0} c ^ 2 \ simeq 2 \ 10 बार 10 ^ {- 9} erg \: cm ^ {- 3} $ $
इस प्रकार, उपरोक्त गणना से, हम देखते हैं कि हम एक पदार्थ-प्रभुत्व वाले ब्रह्मांड में रहते हैं। यह इस तथ्य से समर्थित हो सकता है कि सीएमबी बहुत ठंडा है। जैसा कि हम समय में पीछे देखते हैं, हमारे पास सीएमबी तापमान अधिक गर्म होता जा रहा है, और यह निष्कर्ष निकालने में सक्षम होगा कि एक युग हो सकता है जहां ब्रह्मांड विकिरण का प्रभुत्व था।
घनत्व और स्केल फैक्टर का परिवर्तन
द्रव समीकरण हमें दिखाता है कि -
$ $ \ _ {\ rho} + 3 \ frac {\ _ {a}} {a} \ बाएँ (\ rho + \ frac {P} {c ^ 2} \ right) = 0 $ $
यदि हम एक धूल भरे ब्रह्मांड पर विचार करते हैं, तो हमारे पास P = 0. पिछले परिणामों को अलग करते हुए, हम ब्रह्मांड को विकिरण के प्रभुत्व के रूप में मानते हैं।
$ $ \ _ {\ _ rho} _ {rad} + 3 \ frac {\ _ {a}} {a} \ बाईं (\ rho_ {rad} + \ frac {P} {c ^ 2} \ right) = 0 $$
$ P_ {rad} = \ rho c ^ {2/3} $ हमारे पास के दबाव संबंध का उपयोग करते हुए -
$$ \ डॉट {\ rho} _ {rad} + 3 \ frac {\ _ {a}} {a} \ left (\ rho_ {rad} + \ frac {\ rho_ {rad}} {3} \ right) = 0 $ $
$ $ \ _ \ _ rho} _ {rad} + 4 \ frac {\ _ {a}} {a} (\ rho_ {rad}) = 0 $ $
आगे सरलीकरण पर, हमारे पास,
$$ \ frac {1} {a ^ 4} \ frac {\ mathrm {d}} {\ mathrm {d} t} (\ rho_ {rad} a ^ 4) = 0 $ $
$$ \ rho_ {rad} a ^ 4 = \: निरंतर $$
$$ \ rho_ {rad} \ propto \ frac {1} {a ^ 4} $ $
उपरोक्त परिणाम $ \ rho $ के साथ उलटा 4 वें शक्ति भिन्नता दिखाता है ।
इसकी भौतिक रूप से व्याख्या की जा सकती है, क्योंकि $ A ^ {- 3} $ की मात्रा में भिन्नता आने से यह बढ़ता है। शेष $ a ^ {- 1} $ को ब्रह्मांड में अंतरिक्ष के विस्तार के कारण फोटॉन द्वारा खोई गई ऊर्जा के रूप में माना जा सकता है (कॉस्मोलॉजिकल रिडफ़्ट 1 + z = a -1 )।
निम्नलिखित छवि समय के साथ पदार्थ और विकिरण घनत्व की भिन्नता को दर्शाती है।
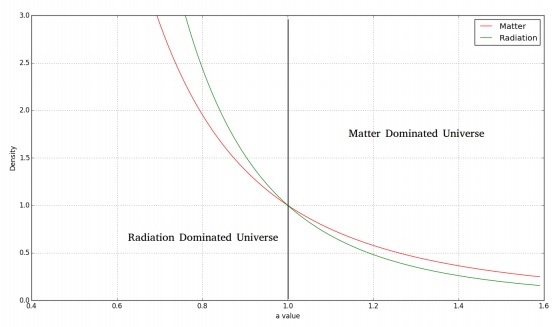
एक फ्लैट, विकिरण प्रभुत्व वाले ब्रह्मांड के लिए, हमारे पास फ्रीडमैन समीकरण इस प्रकार होगा -
$ $ \ बा (\ frac {\ _ {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G \ rho} {3} $ $
$ $ \ बाईं (\ frac {\ _ {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ frac {\ rho_0} {a ^ 4} $ $
सरलीकरण समीकरण के समाधान को सरल बनाने और लागू करने पर, हमारे पास है -
$ $ (\ डॉट {a}) ^ 2 = \ frac {8 \ pi G \ rho_0} {3a ^ 2} $ $
$$ \ Rightarrow a (t) \ propto t ^ {\ frac {1} {2}} $ $
इस प्रकार, हमारे पास है -
$$ a (t) = a_0 \ left (\ frac {t} {t_0} \ right) ^ {\ frac {1} {2}} $$
उपरोक्त समीकरण से, हम देखते हैं कि पैमाने कारक की वृद्धि की दर धूल भरे ब्रह्मांड की तुलना में छोटी है।
याद दिलाने के संकेत
वर्तमान ब्रह्मांड में प्रचलित विकिरण को तारकीय स्रोतों के लिए बहुत कम जिम्मेदार ठहराया जा सकता है।
धूल भरे ब्रह्मांड के लिए, दबाव शून्य है।
सीएमबी बहुत ठंडा है।