디지털 산술 회로
이 장에서는 이진 가산기 및 이진 감산기와 같은 기본 산술 회로에 대해 논의하겠습니다. 이 회로는 이진 값 0과 1로 작동 할 수 있습니다.
이진 가산기
가장 기본적인 산술 연산은 덧셈입니다. 두 이진수를 더하는 회로는 다음과 같이 알려져 있습니다.Binary adder. 먼저 2 비트를 더하는 가산기를 구현해 보겠습니다.
반가산기
Half adder는 두 개의 이진수 A와 B를 더하는 조합 회로입니다. single bit. 두 개의 출력 합계, S 및 캐리, C를 생성합니다.
그만큼 Truth table 반가산기의 값은 아래와 같습니다.
| 입력 | 출력 | ||
|---|---|---|---|
| ㅏ | 비 | 씨 | 에스 |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
두 비트를 더하면 결과 합계는 10 진수로 0에서 2까지의 값을 가질 수 있습니다. 이진수로 단일 비트로 십진수 0과 1을 나타낼 수 있습니다. 그러나 우리는 이진수로 단일 비트로 십진수 2를 나타낼 수 없습니다. 그래서 우리는 그것을 이진으로 표현하기 위해 2 비트가 필요합니다.
S는 최하위 비트 및 캐리이고, C는 결과 합계의 최상위 비트입니다. 처음 세 가지 입력 조합의 경우 carry, C는 0이고 S의 값은 0 또는 1이됩니다.number of ones입력에 존재합니다. 그러나 마지막 입력 조합의 경우 결과 합이 2이므로 carry, C는 1이고 sum, S는 0입니다.
Truth 테이블에서 직접 작성할 수 있습니다. Boolean functions 각 출력에 대해
$$ S = A \ oplus B $$
$ C = AB $
2 입력 Ex-OR 게이트와 2 입력 AND 게이트로 위의 기능을 구현할 수 있습니다. 그만큼circuit diagram 하프 가산기의 값은 다음 그림과 같습니다.

위의 회로에서 두 개의 입력 Ex-OR 게이트와 두 개의 입력 AND 게이트는 각각 합계, S 및 캐리, C를 생성합니다. 따라서 Half-adder는 2 비트의 추가를 수행합니다.
완전 가산기
완전 가산기는 조합 회로로, addition of three bitsA, B 및 C 에서 . 여기서 A와 B는 두 개의 병렬 유효 비트이고 C in 은 이전 단계에서 생성 된 캐리 비트입니다. 이 Full adder는 또한 Half adder와 유사한 두 개의 출력 합계, S & carry, C out 을 생성합니다.
그만큼 Truth table Full adder의 값은 아래와 같습니다.
| 입력 | 출력 | |||
|---|---|---|---|---|
| A | B | Cin | Cout | S |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
3 비트를 더하면 결과 합계는 10 진수로 0에서 3까지의 값을 가질 수 있습니다. 이진수로 단일 비트로 십진수 0과 1을 나타낼 수 있습니다. 그러나 우리는 이진수로 된 단일 비트로 십진수 2와 3을 나타낼 수 없습니다. 그래서 우리는 이진법으로 두 십진수를 표현하기 위해 두 비트가 필요합니다.
S는 최하위 비트이고 수행하고, C out 은 결과 합계의 최상위 비트입니다. 진리표의 모든 입력 조합에 대한 출력 값을 채우는 것은 쉽습니다. 그냥 세어number of ones입력에 존재하고 출력에 동등한 이진수를 씁니다. C in 이 0이면 전체 가산기 진리표는 반가산기 진리표와 동일합니다.
우리는 다음을 얻을 것입니다 Boolean functions 단순화 후 각 출력에 대해.
$$ S = A \ oplus B \ oplus C_ {in} $$
$ c_ {out} = AB + \ left (A \ oplus B \ right) c_ {in} $
입력에 홀수의 1이있을 때 합계 S는 1과 같습니다. Ex-OR 게이트가 홀수 함수 인 출력을 생성한다는 것을 알고 있습니다. 따라서 합계 S를 생성하기 위해 2 개의 2 입력 Ex-OR 게이트 또는 1 개의 3 입력 Ex-OR 게이트를 사용할 수 있습니다. 2 개의 2 입력 AND 게이트와 1 개의 OR 게이트를 사용하여 carry, C out 을 구현할 수 있습니다 . 그만큼circuit diagram Full adder의 값은 다음 그림과 같습니다.
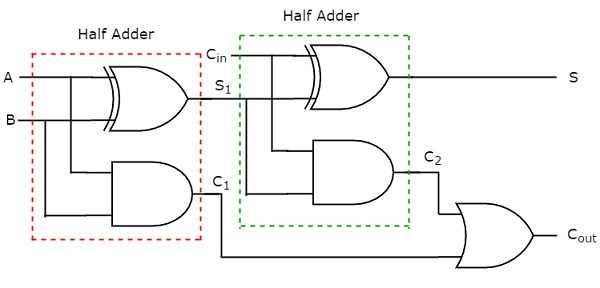
이 가산기는 다음과 같이 호출됩니다. Full adder하나의 Full adder를 구현하려면 두 개의 Half adder와 하나의 OR 게이트가 필요하기 때문입니다. C in 이 0이면 Full adder는 Half adder가됩니다. 위의 회로도 또는 Full adder 출력의 Boolean 함수에서 쉽게 확인할 수 있습니다.
4 비트 이진 가산기
4 비트 이진 가산기는 다음을 수행합니다. addition of two 4-bit numbers. 4 비트 이진수 $ A = A_ {3} A_ {2} A_ {1} A_ {0} $ 및 $ B = B_ {3} B_ {2} B_ {1} B_ {0} $를 지정합니다. 다음 두 가지 방법 중 하나로 4 비트 이진 가산기를 구현할 수 있습니다.
두 개의 최하위 비트를 추가하려면 하나의 절반 가산기를 사용하고 세 개의 상위 비트를 추가하려면 세 개의 전체 가산기를 사용하십시오.
균일 성을 위해 4 개의 완전 가산기를 사용합니다. 초기 carry C in 은 0이므로 최하위 비트를 추가하는 데 사용되는 Full adder는 Half adder가됩니다.
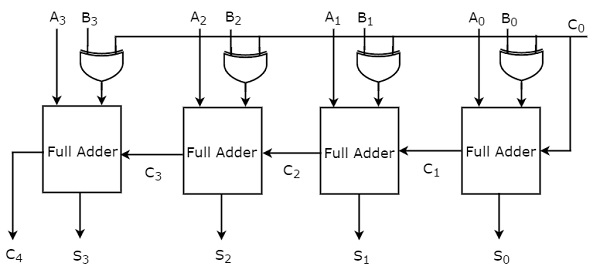
당분간 우리는 두 번째 접근 방식을 고려했습니다. 그만큼block diagram 4 비트 이진 가산기의 그림은 다음과 같습니다.

여기에서 4 개의 전체 가산기가 계단식으로 연결됩니다. 각 전체 가산기는 두 개의 병렬 입력 A 및 B의 각 비트를 가져옵니다. 하나의 전체 가산기의 캐리 출력은 후속 고차 전체 가산기의 캐리 입력이됩니다. 이 4 비트 이진 가산기는 최대 5 비트를 갖는 결과 합계를 생성합니다. 따라서 마지막 단계에서 수행하면 전체 가산기가 MSB가됩니다.
이런 식으로 필요한 수의 전체 가산기를 계단식으로 연결하여 고차 이진 가산기를 구현할 수 있습니다. 이 이진 가산기는 다음과 같이 불립니다.ripple carry (binary) adder 캐리가 한 단계에서 다음 단계로 전파되기 때문입니다.
이진 감산기
두 이진수를 빼는 회로는 다음과 같이 알려져 있습니다. Binary subtractor. Binary subtractor는 다음 두 가지 방법으로 구현할 수 있습니다.
- 캐스케이드 전체 감산기
- 2의 보수 방법
첫 번째 방법에서는 'n'전체 감산기를 계단식으로 연결하여 n 비트 이진 감산기를 얻습니다. 따라서 먼저 Half adder & Full adder와 유사한 Half subtractor와 Full subtractor를 구현할 수 있습니다. 그런 다음 'n'전체 감산기를 계단식으로 연결하여 n 비트 이진 감산기를 구현할 수 있습니다. 그래서, 우리는 두 이진수의 이진수 더하기와 빼기를 위해 두 개의 분리 된 회로를 갖게 될 것입니다.
두 번째 방법에서는 두 번째 입력에서 약간의 수정을 수행하여 두 이진수를 뺄 때 동일한 이진 가산기를 사용할 수 있습니다. 따라서 내부적으로 이진 덧셈 연산이 발생하지만 출력은 결과 뺄셈입니다.
두 이진수 A와 B의 빼기는 다음과 같이 쓸 수 있습니다.
$$ AB = A + \ 왼쪽 ({2}의 \ : 칭찬 \ : of \ : B \ 오른쪽) $$
$ \ Rightarrow AB = A + \ left ({1}의 \ : 칭찬 \ : of \ : B \ right) + 1 $
4 비트 이진 감산기
4 비트 이진 감산기는 다음을 생성합니다. subtraction of two 4-bit numbers. 4 비트 이진수 $ A = A_ {3} A_ {2} A_ {1} A_ {0} $ 및 $ B = B_ {3} B_ {2} B_ {1} B_ {0} $를 지정합니다. 내부적으로 4 비트 이진 감산기의 작동은 4 비트 이진 가산기의 작동과 유사합니다. 이진수 A의 일반 비트, 이진수 B의 보완 비트 및 초기 캐리 (차용), C in 을 1로 4 비트 이진 가산기에 적용하면 4 비트 이진 감산기가됩니다. 그만큼block diagram 4 비트 이진 감산기의 그림은 다음과 같습니다.

이 4 비트 이진 감산기는 최대 5 비트를 갖는 출력을 생성합니다. 이진수 A가 이진수 B보다 크면 출력의 MSB는 0이고 나머지 비트는 AB의 크기를 유지합니다. 이진수 A가 이진수 B보다 작 으면 출력의 MSB는 1입니다. 따라서 AB의 크기를 얻기 위해 출력의 2의 보수를 취하십시오.
이런 식으로 필요한 수정으로 필요한 수의 전체 가산기를 계단식으로 연결하여 고차 이진 감산기를 구현할 수 있습니다.
이진 가산기 / 감산기
언제든지 두 이진수의 더하기 또는 빼기를 수행하는 데 사용할 수있는 회로는 다음과 같이 알려져 있습니다. Binary Adder / subtractor. 이진 가산기와 이진 감산기 모두 계단식으로 연결된 전체 가산기 세트를 포함합니다. 이진수 A의 입력 비트는 이진 가산기와 이진 감산기에 직접 적용됩니다.
이진 가산기와 이진 감산기에 존재하는 완전 가산기의 입력에는 두 가지 차이점이 있습니다.
이진수 B의 입력 비트는 이진 가산기의 전체 가산기에 직접 적용되는 반면, 이진수 B의 보완 비트는 이진 감산기의 전체 가산기에 적용됩니다.
초기 캐리, C 0 = 0은 4 비트 이진 가산기에 적용되는 반면, 초기 캐리 (차용), C 0 = 1은 4 비트 이진 감산기에 적용됩니다.
우리는 2-input Ex-OR gate다른 입력이 0 일 때 첫 번째 입력과 동일한 출력을 생성합니다. 마찬가지로 다른 입력이 1 일 때 첫 번째 입력을 보완하는 출력을 생성합니다.
따라서 이진수 B의 입력 비트를 2 입력 Ex-OR 게이트에 적용 할 수 있습니다. 이 모든 Ex-OR 게이트에 대한 다른 입력은 C 0 입니다. 따라서 C 0 의 값을 기반으로 Ex-OR 게이트는 이진수 B의 일반 또는 보완 비트를 생성합니다.
4 비트 이진 가산기 / 감산기
4 비트 이진 가산기 / 감산기는 초기 캐리 또는 빌리기 값 0을 기반으로 두 개의 4 비트 숫자를 더하거나 뺍니다 . 4 비트 이진수 $ A = A_ {3} A_ {2} A_ {1} A_ {0} $ 및 $ B = B_ {3} B_ {2} B_ {1} B_ {0} $를 지정합니다. 4 비트 이진 가산기 / 감산기의 작동은 4 비트 이진 가산기 및 4 비트 이진 감산기의 작동과 유사합니다.
이진수 A와 B의 일반 비트 및 초기 캐리 또는 빌리, C 0 을 외부에서 4 비트 이진 가산기로 적용합니다. 그만큼block diagram 4 비트 이진 가산기 / 감산기의 그림은 다음과 같습니다.
초기 캐리, 0 이 0이면 각 완전 가산기는 이진수 A와 B의 일반 비트를 얻습니다. 따라서 4 비트 이진 가산기 / 감산기는 출력을 생성합니다.addition of two binary numbers A & B.
초기 차용인 경우 0 이 1이면 각 완전 가산기는 이진수 A의 일반 비트와 이진수 B의 보완 비트를 얻습니다. 따라서 4 비트 이진 가산기 / 감산기는 출력을 생성합니다.subtraction of two binary numbers A & B.
따라서 추가 Ex-OR 게이트의 도움으로 동일한 회로를 두 이진수의 덧셈과 뺄셈 모두에 사용할 수 있습니다.