디지털 회로-디멀티플렉서
De-MultiplexerMultiplexer의 역 동작을 수행하는 조합 회로입니다. 단일 입력, 'n'선택 라인 및 최대 2n 출력이 있습니다. 입력은 선택 라인의 값에 따라 이러한 출력 중 하나에 연결됩니다.
'n'개의 선택 라인이 있으므로 0과 1의 가능한 조합이 2n 개있을 것 입니다. 따라서 각 조합은 하나의 출력 만 선택할 수 있습니다. De-Multiplexer는De-Mux.
1x4 디멀티플렉서
1x4 디멀티플렉서에는 1 개의 입력 I, 2 개의 선택 라인, s 1 & s 0 및 4 개의 출력 Y 3 , Y 2 , Y 1 & Y 0이 있습니다. 그만큼block diagram 1x4 De-Multiplexer의 그림은 다음과 같습니다.

단일 입력 'I'는 선택 라인 s 1 및 s0 의 값에 따라 Y 3 ~ Y 0 의 4 개 출력 중 하나에 연결됩니다 . 그만큼Truth table 1x4 De-Multiplexer의 그림은 아래와 같습니다.
| 선택 입력 | 출력 | ||||
|---|---|---|---|---|---|
| S1 | S0 | Y3 | Y2 | Y1 | Y0 |
| 0 | 0 | 0 | 0 | 0 | I |
| 0 | 1 | 0 | 0 | I | 0 |
| 1 | 0 | 0 | I | 0 | 0 |
| 1 | 1 | I | 0 | 0 | 0 |
위의 진리표에서 우리는 직접 Boolean functions 각 출력에 대해
$$ Y_ {3} = s_ {1} s_ {0} I $$
$$ Y_ {2} = s_ {1} {s_ {0}} 'I $$
$$ Y_ {1} = {s_ {1}} 's_ {0} I $$
$$ Y_ {0} = {s_1} '{s_ {0}}'I $$
인버터 및 3 입력 AND 게이트를 사용하여 이러한 부울 함수를 구현할 수 있습니다. 그만큼circuit diagram 1x4 De-Multiplexer의 그림은 다음과 같습니다.

위 회로의 동작을 쉽게 이해할 수 있습니다. 마찬가지로 동일한 절차에 따라 1x8 De-Multiplexer 및 1x16 De-Multiplexer를 구현할 수 있습니다.
고차 디멀티플렉서 구현
이제 하위 디멀티플렉서를 사용하여 다음 두 개의 상위 디멀티플렉서를 구현해 보겠습니다.
- 1x8 디멀티플렉서
- 1x16 디멀티플렉서
1x8 디멀티플렉서
이 섹션에서는 1x4 De-Multiplexer와 1x2 De-Multiplexer를 사용하여 1x8 De-Multiplexer를 구현해 보겠습니다. 1x4 디멀티플렉서에는 단일 입력, 2 개의 선택 라인 및 4 개의 출력이 있다는 것을 알고 있습니다. 반면 1x8 De-Multiplexer에는 단일 입력, 3 개의 선택 라인 및 8 개의 출력이 있습니다.
그래서 우리는 1x4 De-Multiplexers최종 8 개의 출력을 얻기 위해 두 번째 단계에서. 두 번째 단계의 입력 개수는 2 개이므로1x2 DeMultiplexer첫 번째 단계에서 첫 번째 단계의 출력이 두 번째 단계의 입력이되도록합니다. 이 1x2 디멀티플렉서의 입력은 1x8 디멀티플렉서의 전체 입력이됩니다.
1x8 디멀티플렉서에 하나의 입력 I, 세 개의 선택 라인 s 2 , s 1 & s 0 및 출력 Y 7 ~ Y 0 을 갖도록 합니다. 그만큼Truth table 1x8 De-Multiplexer의 그림은 아래와 같습니다.
| 선택 입력 | 출력 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| s2 | s1 | s0 | Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | I |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | I | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | I | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | I | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | I | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | I | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
위의 Truth 테이블을 고려하면 더 낮은 차수의 Multiplexer를 사용하여 1x8 De-Multiplexer를 쉽게 구현할 수 있습니다. 그만큼block diagram 1x8 De-Multiplexer의 그림은 다음과 같습니다.

흔한 selection lines, s1 & s01x4 디멀티플렉서 모두에 적용됩니다. 상단 1x4 디멀티플렉서의 출력은 Y 7 ~ Y 4 이고 하단 1x4 디멀티플렉서의 출력은 Y 3 ~ Y 0 입니다.
다른 selection line, s21x2 De-Multiplexer에 적용됩니다. s 2 가 0이면 선택 라인 s 1 & s 0 의 값에 따라 하위 1x4 디멀티플렉서의 4 개 출력 중 하나가 input, I과 같습니다 . 마찬가지로 s 2 가 1이면 상위 1x4 DeMultiplexer의 4 개 출력 중 하나는 선택 라인 s 1 & s 0 의 값을 기반으로하는 input, I과 같습니다 .
1x16 디멀티플렉서
이 섹션에서는 1x8 De-Multiplexer와 1x2 De-Multiplexer를 사용하여 1x16 De-Multiplexer를 구현해 보겠습니다. 1x8 De-Multiplexer에는 단일 입력, 3 개의 선택 라인 및 8 개의 출력이 있습니다. 반면 1x16 De-Multiplexer에는 단일 입력, 4 개의 선택 라인 및 16 개의 출력이 있습니다.
그래서 우리는 1x8 De-Multiplexers두 번째 단계에서 최종 16 개의 출력을 얻습니다. 두 번째 단계의 입력 개수는 2 개이므로1x2 DeMultiplexer첫 번째 단계에서 첫 번째 단계의 출력이 두 번째 단계의 입력이되도록합니다. 이 1x2 De-Multiplexer의 입력은 1x16 De-Multiplexer의 전체 입력이됩니다.
1x16 디멀티플렉서에 1 개의 입력 I, 4 개의 선택 라인 s 3 , s 2 , s 1 & s 0 및 출력 Y 15 ~ Y 0을 갖습니다 . 그만큼block diagram 하위 멀티플렉서를 사용하는 1x16 De-Multiplexer의 그림은 다음과 같습니다.
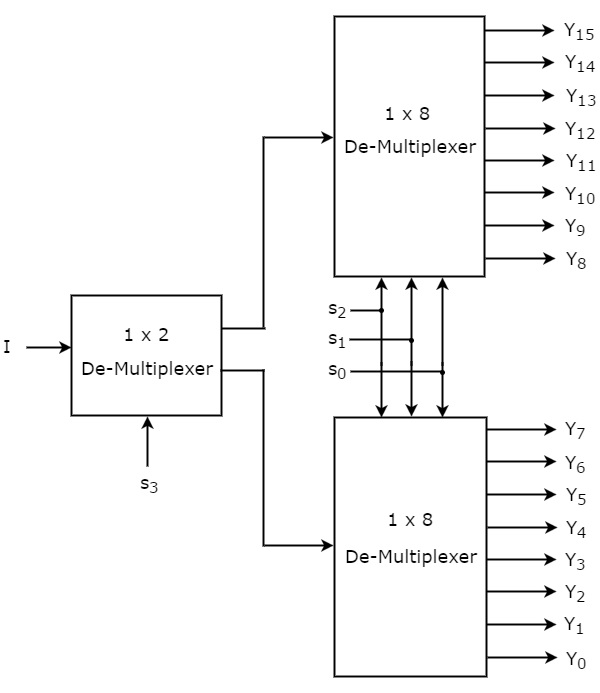
흔한 selection lines s2, s1 & s01x8 디멀티플렉서 모두에 적용됩니다. 상위 1x8 디멀티플렉서의 출력 은 Y 15 ~ Y 8 이고 하위 1x8 디멀티플렉서의 출력은 Y 7 ~ Y 0 입니다.
다른 selection line, s31x2 De-Multiplexer에 적용됩니다. s 3 이 0이면 선택 라인 s 2 , s 1 & s 0 의 값에 따라 하위 1x8 디멀티플렉서의 8 개 출력 중 하나가 input, I와 같습니다 . 마찬가지로, s3이 1이면 상위 1x8 디멀티플렉서의 8 개 출력 중 하나는 선택 라인 s 2 , s 1 & s 0 의 값을 기반으로 입력 I와 같습니다 .