디지털 회로-인코더
안 EncoderDecoder의 역 동작을 수행하는 조합 회로입니다. 최대 2n 개의 입력 라인과 'n'개의 출력 라인이 있습니다. 입력에 해당하는 이진 코드를 생성하며 이는 활성 High입니다. 따라서 인코더는 'n'비트로 2n 개의 입력 라인을 인코딩 합니다. 인코더에서 활성화 신호를 나타내는 것은 선택 사항입니다.
4 ~ 2 인코더
4 대 2 인코더에 4 개의 입력 Y 3 , Y 2 , Y 1 & Y 0 과 2 개의 출력 A 1 & A 0 이 있다고 가정 합니다. 그만큼block diagram 다음 그림은 4 ~ 2 인코더 중 하나입니다.

출력에서 각 이진 코드를 얻기 위해 언제든지이 4 개의 입력 중 하나만 '1'이 될 수 있습니다. 그만큼Truth table 4 ~ 2 엔코더의 그림은 아래와 같습니다.
| 입력 | 출력 | ||||
|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
Truth 테이블에서 우리는 Boolean functions 각 출력에 대해
$$ A_ {1} = Y_ {3} + Y_ {2} $$
$$ A_ {0} = Y_ {3} + Y_ {1} $$
두 개의 입력 OR 게이트를 사용하여 위의 두 가지 부울 함수를 구현할 수 있습니다. 그만큼circuit diagram 4 ~ 2 엔코더의 구성은 다음 그림과 같습니다.

위의 회로도에는 두 개의 OR 게이트가 있습니다. 이러한 OR 게이트는 4 개의 입력을 2 비트로 인코딩합니다.
이진 인코더에 8 진법
Octal to binary 인코더에는 8 개의 입력, Y 7 ~ Y 0 및 3 개의 출력 A 2 , A 1 & A 0이 있습니다. 8 진법 인코더는 8 ~ 3 인코더 일뿐입니다. 그만큼block diagram 다음 그림은 8 진수에서 2 진 인코더로의 변환을 보여줍니다.
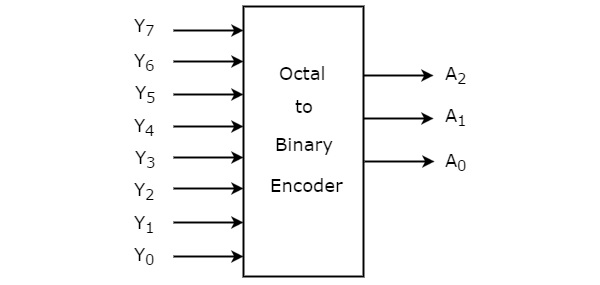
언제든지 각 이진 코드를 얻기 위해 8 개의 입력 중 하나만 '1'이 될 수 있습니다. 그만큼Truth table 8 진수에서 이진 인코더로의 값은 아래와 같습니다.
| 입력 | 출력 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 | A2 | A1 | A0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
Truth 테이블에서 우리는 Boolean functions 각 출력에 대해
$$ A_ {2} = Y_ {7} + Y_ {6} + Y_ {5} + Y_ {4} $$
$$ A_ {1} = Y_ {7} + Y_ {6} + Y_ {3} + Y_ {2} $$
$$ A_ {0} = Y_ {7} + Y_ {5} + Y_ {3} + Y_ {1} $$
4 개의 입력 OR 게이트를 사용하여 위의 부울 함수를 구현할 수 있습니다. 그만큼circuit diagram 다음 그림은 8 진수에서 2 진 인코더로의 변환을 보여줍니다.

위의 회로도에는 3 개의 4 입력 OR 게이트가 있습니다. 이러한 OR 게이트는 8 개의 입력을 3 비트로 인코딩합니다.
인코더의 단점
다음은 일반 인코더의 단점입니다.
인코더의 모든 출력이 0 일 때 모호함이 있습니다. 왜냐하면 최하위 입력 만 1이거나 모든 입력이 0 일 때 입력에 해당하는 코드 일 수 있기 때문입니다.
둘 이상의 입력이 높음으로 활성화되면 인코더는 올바른 코드가 아닐 수있는 출력을 생성합니다. 에 대한example, Y 3 및 Y 6 모두 '1'이면 인코더는 출력에서 111을 생성합니다. '1'인 경우 Y 3 에 해당하는 등가 코드도 '1' 인 경우 Y 6에 해당하는 등가 코드도 아닙니다 .
따라서 이러한 어려움을 극복하려면 인코더의 각 입력에 우선 순위를 할당해야합니다. 그러면 인코더의 출력은 우선 순위가 더 높은 활성 High 입력에 해당하는 (이진) 코드가됩니다. 이 인코더는priority encoder.
우선 순위 인코더
4 ~ 2 우선 순위 인코더에는 4 개의 입력 Y 3 , Y 2 , Y 1 & Y 0 과 2 개의 출력 A 1 & A 0이 있습니다. 여기서 입력 Y 3 은 가장 높은 우선 순위를 갖는 반면 입력 Y 0 은 가장 낮은 우선 순위를 갖습니다. 이 경우 두 개 이상의 입력이 동시에 '1'이 되더라도 출력은 입력에 해당하는 (이진) 코드가됩니다.higher priority.
우리는 하나 더 고려했습니다 output, V 출력에서 사용 가능한 코드가 유효한지 여부를 알기 위해.
인코더의 입력 중 하나 이상이 '1'이면 출력에서 사용할 수있는 코드가 유효한 코드입니다. 이 경우 출력 V는 1과 같습니다.
인코더의 모든 입력이 '0'이면 출력에서 사용할 수있는 코드가 유효한 코드가 아닙니다. 이 경우 출력 V는 0과 같습니다.
그만큼 Truth table 4 ~ 2 우선 순위 인코더의 아래에 나와 있습니다.
| 입력 | 출력 | |||||
|---|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 | V |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 엑스 | 0 | 1 | 1 |
| 0 | 1 | 엑스 | 엑스 | 1 | 0 | 1 |
| 1 | 엑스 | 엑스 | 엑스 | 1 | 1 | 1 |
사용하다 4 variable K-maps 각 출력에 대한 단순화 된 표현을 얻기 위해.
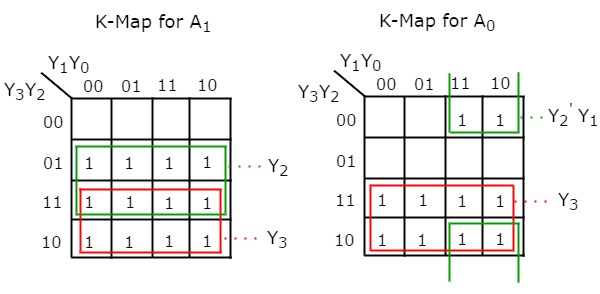
단순화 Boolean functions 아르
$$ A_ {1} = Y_ {3} + Y_ {2} $$
$ A_ {0} = Y_ {3} + {Y_ {2}} 'Y_ {1} $
마찬가지로 출력의 부울 함수 V를 다음과 같이 얻습니다.
$$ V = Y_ {3} + Y_ {2} + Y_ {1} + Y_ {0} $$
논리 게이트를 사용하여 위의 부울 함수를 구현할 수 있습니다. 그만큼circuit diagram 4 ~ 2 우선 순위 인코더의 다음 그림에 나와 있습니다.

위의 회로도에는 2 개의 2 입력 OR 게이트, 1 개의 4 입력 OR 게이트, 1 개의 2 입력 AND 게이트 및 1 개의 인버터가 포함되어 있습니다. 여기서 AND 게이트 및 인버터 조합은 여러 입력이 동시에 '1'과 동일한 경우에도 출력에서 유효한 코드를 생성하는 데 사용됩니다. 따라서이 회로는 4 개의 입력을 2 비트로 인코딩합니다.priority 각 입력에 할당됩니다.