디지털 회로-K-Map 방법
이전 장에서는 부울 가정과 정리를 사용하여 부울 함수를 단순화했습니다. 시간이 많이 걸리는 과정이며 각 단계 후에 단순화 된 표현을 다시 작성해야합니다.
이 어려움을 극복하기 위해 Karnaugh부울 함수를 쉽게 단순화하는 방법을 도입했습니다. 이 방법을 Karnaugh 맵 방법 또는 K- 맵 방법이라고합니다. 'n'변수에 대해 2n 개의 셀로 구성된 그래픽 방법 입니다. 인접한 셀은 단일 비트 위치에서만 다릅니다.
2 ~ 5 개의 변수에 대한 K- 맵
K-Map 방법은 2 개 변수의 부울 함수를 5 개 변수로 최소화하는 데 가장 적합합니다. 이제 2 ~ 5 개의 변수에 대한 K-Map에 대해 하나씩 논의 해 보겠습니다.
2 가변 K-Map
2 개의 변수 K-map의 셀 수는 변수의 수가 2 개이므로 4 개입니다. 다음 그림은2 variable K-Map.
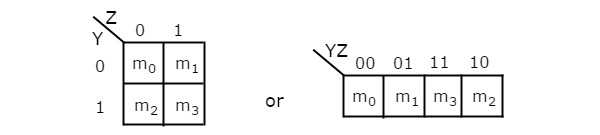
4 개의 인접한 최소 항을 그룹화 할 수있는 가능성은 하나뿐입니다.
2 개의 인접한 min 항을 그룹화 할 수있는 조합은 {(m 0 , m 1 ), (m 2 , m 3 ), (m 0 , m 2 ) 및 (m 1 , m 3 )}입니다.
3 가변 K-Map
변수의 수가 3 개이므로 3 개의 변수 K- 맵의 셀 수는 8 개입니다. 다음 그림은3 variable K-Map.
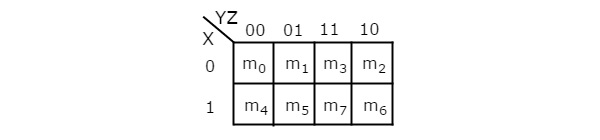
8 개의 인접한 최소 항을 그룹화 할 수있는 가능성은 하나뿐입니다.
4 개의 인접한 min 항을 그룹화 할 수있는 조합은 {(m 0 , m 1 , m 3 , m 2 ), (m 4 , m 5 , m 7 , m 6 ), (m 0 , m 1 , m 4 , m 5 ), (m 1 , m 3 , m 5 , m 7 ), (m 3 , m 2 , m 7 , m 6 ) 및 (m 2 , m 0 , m 6 , m 4 )}.
2 개의 인접한 min 항을 그룹화 할 수있는 조합은 {(m 0 , m 1 ), (m 1 , m 3 ), (m 3 , m 2 ), (m 2 , m 0 ), (m 4 , m 5 )입니다. , (m 5 , m 7 ), (m 7 , m 6 ), (m 6 , m 4 ), (m 0 , m 4 ), (m 1 , m 5 ), (m 3 , m 7 ) 및 ( m 2 , m 6 )}.
x = 0이면 3 개의 변수 K- 맵이 2 개의 변수 K- 맵이됩니다.
4 가변 K-Map
변수의 수가 4 개이므로 4 개의 변수 K- 맵의 셀 수는 16 개입니다. 다음 그림은4 variable K-Map.
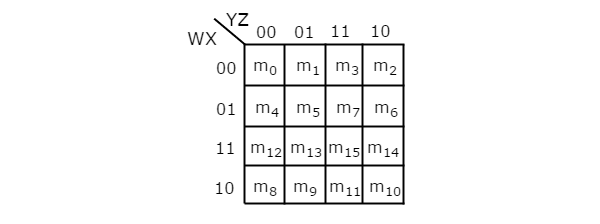
16 개의 인접한 최소 항을 그룹화 할 수있는 가능성은 하나뿐입니다.
R 1 , R 2 , R 3 및 R 4 는 각각 첫 번째 행, 두 번째 행, 세 번째 행 및 네 번째 행의 최소 항을 나타냅니다. 마찬가지로 C 1 , C 2 , C 3 및 C 4 는 각각 첫 번째 열, 두 번째 열, 세 번째 열 및 네 번째 열의 최소 항을 나타냅니다. 8 개의 인접한 min 항을 그룹화 할 수있는 조합은 {(R 1 , R 2 ), (R 2 , R 3 ), (R 3 , R 4 ), (R 4 , R 1 ), (C 1 , C 2 )입니다. , (C 2 , C 3 ), (C 3 , C 4 ), (C 4 , C 1 )}.
w = 0이면 4 개의 변수 K- 맵이 3 개의 변수 K- 맵이됩니다.
5 가변 K-Map
5 개 변수 K-map의 셀 수는 변수 수가 5 개이므로 32 개입니다. 다음 그림은 5 variable K-Map.

32 개의 인접한 최소 항을 그룹화 할 수있는 가능성은 하나뿐입니다.
16 개의 인접한 최소 항을 그룹화하는 두 가지 가능성이 있습니다. 즉, m 0 에서 m 15 및 m 16 에서 m 31 까지의 최소 항 그룹화 .
v = 0이면 5 개의 변수 K- 맵이 4 개의 변수 K- 맵이됩니다.
위의 모든 K- 맵에서 최소 용어 표기법 만 사용했습니다. 마찬가지로 Max 용어 표기법 만 사용할 수 있습니다.
K-Maps를 사용한 부울 함수 최소화
Boolean 함수가 '1'인 입력 조합을 고려하면 Boolean 함수를 얻을 수 있습니다. standard sum of products K-map을 단순화 한 후 양식.
마찬가지로, Boolean 함수가 '0'인 입력 조합을 고려하면 Boolean 함수를 얻을 수 있습니다. standard product of sums K-map을 단순화 한 후 양식.
다음을 따르십시오 rules for simplifying K-maps 제품의 표준 합계 양식을 얻으려면.
부울 함수에있는 변수 수를 기반으로 각 K 맵을 선택합니다.
부울 함수가 최소 항의 합으로 주어지면 K- 맵의 각 최소 항 셀에 배치합니다. 부울 함수가 제품의 합계 형식으로 제공되는 경우 주어진 제품 용어가 유효한 K- 맵의 가능한 모든 셀에 해당 항목을 배치합니다.
인접한 최대 수를 그룹화 할 수 있는지 확인하십시오. 2의 거듭 제곱이어야합니다. 가장 높은 2의 거듭 제곱과 최소 2의 제곱에서 시작합니다. 최고 검정력은 K- 맵에서 고려되는 변수의 수와 같고 최소 검정력은 0입니다.
각 그룹은 리터럴 또는 하나의 제품 용어를 제공합니다. 그것은prime implicant. 주요 함의는 다음과 같다.essential prime implicant, '1'하나 이상이 다른 그룹에 포함되지 않고 해당 그룹 만 포함되는 경우.
모든 주요 함축 및 필수 주요 함축을 기록하십시오. 단순화 된 부울 함수에는 모든 필수 프라임 임 플리 던트와 필수 프라임 임 플리 컨트 만 포함됩니다.
Note 1 − 일부 입력 조합에 대해 출력이 정의되지 않은 경우 해당 출력 값은 다음과 같이 표시됩니다. don’t care symbol ‘x’. 즉, '0'또는 '1'로 간주 할 수 있습니다.
Note 2− do n't care 용어도있는 경우 K-map의 각 셀에 do n't care 'x'를 배치합니다. 인접 항목의 최대 수를 그룹화하는 데 도움이되는 상관 안함 'x'만 고려하십시오. 이러한 경우에는 상관 없음 값을 '1'로 취급하십시오.
예
하자 simplify 다음 부울 함수, f(W, X, Y, Z)= WX’Y’ + WY + W’YZ’ K-map 사용.
주어진 부울 함수는 제품 형태의 합계입니다. 4 개의 변수 W, X, Y & Z가 있습니다. 따라서4 variable K-map. 그만큼4 variable K-map 주어진 제품 용어에 해당하는 항목이 다음 그림에 나와 있습니다.
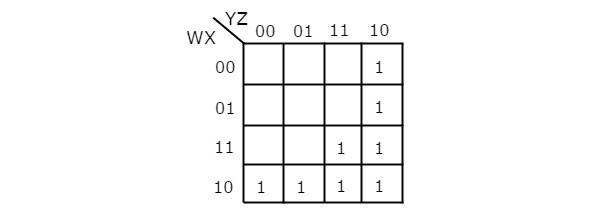
여기서 1은 K-map의 다음 셀에 배치됩니다.
행 4와 열 1 및 2의 교차점에 공통되는 셀은 제품 용어에 해당합니다. WX’Y’.
행 3 및 4와 열 3 및 4의 교차점에 공통되는 셀은 제품 용어에 해당합니다. WY.
행 1과 2와 열 4의 교차점에 공통되는 셀은 제품 용어에 해당합니다. W’YZ’.
인접한 16 개 또는 인접한 8 개를 그룹화 할 수 없습니다. 4 개의 인접한 항목을 그룹화 할 수있는 세 가지 가능성이 있습니다. 이 세 그룹화 후에는 그룹화되지 않은 상태로 남아있는 단일 그룹이 없습니다. 따라서 인접한 2 개의 그룹화를 확인할 필요가 없습니다. 그만큼4 variable K-map 이 세 가지 groupings 다음 그림에 나와 있습니다.

여기에 WX ', WY & YZ'의 세 가지 주요 함의가 있습니다. 이 모든 주요 함의는essential 다음과 같은 이유 때문입니다.
두 사람 (m8 & m9)네 번째 행 그룹은 다른 그룹에 포함되지 않습니다. 네 번째 행 그룹 만이 두 항목을 다룹니다.
하나 하나 (m15)정사각형 모양의 그룹은 다른 그룹에 포함되지 않습니다. 사각형 모양 그룹 만 해당 항목을 다룹니다.
두 사람 (m2 & m6)네 번째 열 그룹의 일부는 다른 그룹에 포함되지 않습니다. 네 번째 열 그룹 만이 두 항목을 다룹니다.
따라서 simplified Boolean function 이다
f = WX’ + WY + YZ’
다음을 따르십시오 rules for simplifying K-maps 합계 형식의 표준 제품을 얻으려면.
부울 함수에있는 변수 수를 기반으로 각 K 맵을 선택합니다.
Boolean 함수가 Max 항의 곱으로 주어지면 K- 맵의 각 Max 항 셀에 0을 배치합니다. 부울 함수가 합계 형식의 곱으로 제공되는 경우 주어진 합계 항이 유효한 K- 맵의 가능한 모든 셀에 0을 배치합니다.
인접한 0의 최대 수를 그룹화 할 수 있는지 확인하십시오. 2의 거듭 제곱이어야합니다. 가장 높은 2의 거듭 제곱과 최소 2의 제곱에서 시작합니다. 최고 검정력은 K- 맵에서 고려되는 변수의 수와 같고 최소 검정력은 0입니다.
각 그룹은 리터럴 또는 하나의 합계 용어를 제공합니다. 그것은prime implicant. 주요 함의는 다음과 같다.essential prime implicant, '0'하나 이상이 다른 그룹에 포함되지 않고 해당 그룹 만 포함되는 경우.
모든 주요 함축 및 필수 주요 함축을 기록하십시오. 단순화 된 부울 함수에는 모든 필수 프라임 임 플리 던트와 필수 프라임 임 플리 컨트 만 포함됩니다.
Note− do n't care 용어도있는 경우 K-map의 각 셀에 do n't care 'x'를 배치합니다. 인접한 0의 최대 수를 그룹화하는 데 도움이되는 상관 안함 'x'만 고려하십시오. 이러한 경우에는 상관 없음 값을 '0'으로 처리하십시오.
예
하자 simplify 다음 부울 함수, $ f \ left (X, Y, Z \ right) = \ prod M \ left (0,1,2,4 \ right) $ 사용.
주어진 부울 함수는 Max 용어 형식의 곱입니다. 3 개의 변수 X, Y, Z가 있습니다. 따라서 3 개의 변수 K- 맵이 필요합니다. 주어진 Max 항은 M 0 , M 1 , M 2 & M 4 입니다. 3variable K-map 주어진 Max 항에 해당하는 0이 다음 그림에 나와 있습니다.

8 개의 인접한 0 또는 4 개의 인접한 0을 그룹화 할 수 없습니다. 2 개의 인접한 0을 그룹화 할 수있는 세 가지 가능성이 있습니다. 이 세 그룹화 후에는 그룹화되지 않은 단일 0이 남지 않습니다. 그만큼3 variable K-map 이 세 가지 groupings 다음 그림에 나와 있습니다.

여기에 세 가지 주요 함축 물 X + Y, Y + Z & Z + X가 있습니다. essential 각 그룹의 하나의 0은 개별 그룹을 제외하고는 다른 그룹에 포함되지 않기 때문입니다.
따라서 simplified Boolean function 이다
f = (X + Y).(Y + Z).(Z + X)
이렇게하면 K-map 방법을 사용하여 최대 5 개의 변수까지 부울 함수를 쉽게 단순화 할 수 있습니다. 5 개 이상의 변수의 경우 K-Maps를 사용하여 기능을 단순화하기가 어렵습니다. 왜냐하면cells K-map에서 doubled 새 변수를 포함합니다.
이 검사 및 인접 항목 (최소 용어) 또는 인접한 0 (최대 용어)의 그룹화는 복잡합니다. 우리는 논의 할 것이다Tabular method K-map 방식의 어려움을 극복하기 위해 다음 장에서