디지털 회로-임계 값 논리
이전 장에서는 논리 게이트를 사용하여 다양한 조합 회로를 구현했습니다. NOT 게이트를 제외하고 나머지 모든 로직 게이트에는 최소 2 개의 입력과 단일 출력이 있습니다. 마찬가지로threshold gate 또한 적어도 하나의 입력과 하나의 출력 만 포함합니다.
또한 각 입력에 대한 각 가중치와 임계 값을 포함합니다. 이러한 가중치와 임계 값은 유한 실수 일 수 있습니다.
임계 값 게이트의 기초
문턱 게이트의 입력을 X 1 , X 2 , X 3 ,…, X n이라고 합니다. 이러한 입력의 해당 가중치는 W 1 , W 2 , W 3 ,…, W n 입니다. 그만큼symbol 문턱 게이트의 값은 다음 그림에 나와 있습니다.
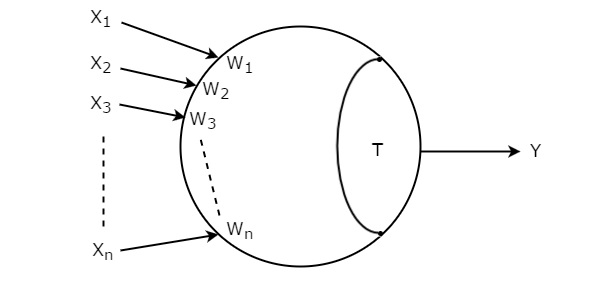
Threshold gate원으로 표시되며 'n'입력, X 1 ~ X n 및 단일 출력, Y를 갖습니다 .이 원은 두 부분으로 구성됩니다. 한 부분은 입력에 해당하는 가중치를 나타내고 다른 부분은 임계 값 T를 나타냅니다.
입력 값과 해당 가중치의 곱의 합은 다음과 같습니다. weighted sum. 이 가중 합계가 임계 값 T보다 크거나 같으면 출력 Y 만 1과 같습니다. 그렇지 않으면 출력 Y는 0이됩니다.
Mathematically, 우리는 Threshold gate의 입력과 출력 간의 관계를 아래와 같이 작성할 수 있습니다.
$$ Y = 1, \ : \ : W_ {1} X_ {1} + W_ {2} X_ {2} + W_ {3} X_ {3} + ... W_ {n} X_ {n} \ geq T $$
= 0, 그렇지 않으면.
따라서 가중치 및 / 또는 임계 값 T의 값을 변경하여 다양한 논리 게이트 및 부울 함수를 구현할 수 있습니다.
예
우리가 simplified Boolean function 다음 임계 값 게이트의 경우.

이 임계 값 게이트에는 3 개의 입력 X 1 , X 2 , X 3 및 1 개의 출력 Y가 있습니다.
입력 X 1 , X 2 및 X 3에 해당하는 가중치 는 각각 W 1 = 2, W 2 = 1 및 W 3 = -4입니다.
Threshold gate의 값은 T = -1입니다.
그만큼 weighted sum 문턱 게이트의
$$ W = W_ {1} X_ {1} + W_ {2} X_ {2} + W_ {3} X_ {3} $$
위 방정식에서 주어진 가중치를 대체하십시오.
$$ \ Rightarrow W = 2X_ {1} + X_ {2} -4X_ {3} $$
임계 값 게이트의 출력, W ≥ -1이면 Y는 '1'이되고, 그렇지 않으면 '0'이됩니다.
다음과 같은 table 가능한 모든 입력 조합에 대한 입력과 출력 간의 관계를 보여줍니다.
| 입력 | 가중 합계 | 산출 | ||
|---|---|---|---|---|
| $ X_ {1} $ | $ X_ {2} $ | $ X_ {3} $ | $ W = 2X_ {1} + X_ {2} -4X_ {3} $ | $ Y $ |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | -4 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | -삼 | 0 |
| 1 | 0 | 0 | 2 | 1 |
| 1 | 0 | 1 | -2 | 0 |
| 1 | 1 | 0 | 삼 | 1 |
| 1 | 1 | 1 | -1 | 1 |
위의 표에서 우리는 Boolean function 출력의 경우 Y는
$$ Y = \ sum m \ left (0,2,4,6,7 \ right) $$
이 부울 함수의 단순화는 3 variable K-Map 다음 그림에 나와 있습니다.

따라서 simplified Boolean function 주어진 임계 값 게이트의 경우 $ Y = {X_ {3} '} + X_ {1} X_ {2} $입니다.
임계 값 함수의 합성
문턱 게이트는 universal gate임계 값 게이트를 사용하여 모든 부울 함수를 구현할 수 있기 때문입니다. 때로는 단일 임계 값 게이트를 사용하여 논리 게이트와 부울 함수를 거의 구현하지 못할 수도 있습니다. 이 경우 여러 임계 값 게이트가 필요할 수 있습니다.
다음을 따르십시오 steps 단일 임계 값 게이트를 사용하여 부울 함수를 구현합니다.
Step 1 − 공식화 Truth table 주어진 부울 함수에 대해.
Step 2 − 위의 Truth 테이블에서 하나 이상의 열을 추가 (포함)하여 다음과 같은 관계를 제공합니다. weighted sums 과 Threshold value.
Step 3 − 아래에 언급 된대로 각 입력 조합에 대한 가중치 합계와 임계 값 간의 관계를 작성합니다.
부울 함수의 출력이 1이면 가중치 합은 해당 입력 조합에 대한 임계 값보다 크거나 같습니다.
부울 함수의 출력이 0이면 가중치 합계는 해당 입력 조합에 대한 임계 값보다 작습니다.
Step 4 − 위 표의 마지막 열에있는 모든 관계를 만족하는 방식으로 가중치 및 임계 값을 선택합니다.
step 5 − 그리기 symbol 그 가중치와 임계 값을 가진 임계 값 게이트의.
예
다음을 구현하겠습니다. Boolean function 단일 임계 값 게이트를 사용합니다.
$$ Y \ 왼쪽 (X_ {1}, X_ {2}, X_ {3} \ 오른쪽) = \ sum m \ 왼쪽 (0,2,4,6,7 \ 오른쪽) $$
주어진 부울 함수는 최소 항의 합으로 표현되는 3 가지 변수 함수입니다. 그만큼Truth table 이 기능에 대한 설명은 다음과 같습니다.
| 입력 | 산출 | ||
|---|---|---|---|
| X1 | X2 | X3 | Y |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
이제 위의 Truth 테이블에 열을 하나 더 추가 (포함)하겠습니다. 이 마지막 열에는weighted sums (W) and Threshold 각 입력 조합에 대한 값 (T).
| 입력 | 산출 | W와 T의 관계 | ||
|---|---|---|---|---|
| X1 | X2 | X3 | Y | |
| 0 | 0 | 0 | 1 | 0 ≥T |
| 0 | 0 | 1 | 0 | 승 3 <T |
| 0 | 1 | 0 | 1 | 승 2 ≥ T |
| 0 | 1 | 1 | 0 | 승 2 + 승 3 <T |
| 1 | 0 | 0 | 1 | 승 1 ≥ T |
| 1 | 0 | 1 | 0 | 승 1 + 승 3 <T |
| 1 | 1 | 0 | 1 | 승 1 + 승 2 ≥ T |
| 1 | 1 | 1 | 1 | 승 1 + 승 2 + 승 3 ≥ T |
다음은 위 표의 결론입니다.
임계 값의 값은 첫 번째 관계를 기반으로 0 또는 음수 여야합니다.
W 3 의 값은 첫 번째 및 두 번째 관계를 기반으로 음수 여야합니다.
W 1 및 W 2의 값은 다섯 번째 및 세 번째 관계를 기반으로하는 임계 값보다 크거나 같아야합니다.
네 번째 관계를 기반으로 W 2 는 W 3 보다 커야 합니다.
위의 결론을 기반으로 가중치 및 임계 값에 대해 다음 값을 선택할 수 있습니다.
승 1 = 2, 승 2 = 1, 승 3 = -4 & T = -1
그만큼 symbol 위의 값을 가진 Threshold gate의 값은 아래와 같습니다.

따라서이 임계 값 게이트는 주어진 Boolean function, $ Y \ left (X_ {1}, X_ {2}, X_ {3} \ right) = \ sum m \ left (0,2,4,6,7 \ right) $.