프로그래밍 가능 논리 장치
프로그래밍 가능 논리 장치 (PLDs)집적 회로입니다. 여기에는 AND 게이트 배열과 또 다른 OR 게이트 배열이 포함됩니다. 프로그래밍 가능한 기능이있는 어레이 유형에 따라 3 가지 종류의 PLD가 있습니다.
- 프로그래밍 가능한 읽기 전용 메모리
- 프로그래밍 가능한 어레이 로직
- 프로그래밍 가능 논리 어레이
이러한 장치에 정보를 입력하는 과정을 programming. 기본적으로 사용자는 요구 사항에 따라 부울 기능을 구현하기 위해 이러한 장치 또는 IC를 전기적으로 프로그래밍 할 수 있습니다. 여기서 프로그래밍이라는 용어는 소프트웨어 프로그래밍이 아닌 하드웨어 프로그래밍을 의미합니다.
프로그래밍 가능 읽기 전용 메모리 (PROM)
ROM (Read Only Memory)은 바이너리 정보를 영구적으로 저장하는 메모리 장치입니다. 즉, 나중에 저장된 정보를 변경할 수 없습니다. ROM에 프로그래밍 가능한 기능이 있으면 다음과 같이 호출됩니다.Programmable ROM (PROM). 사용자는 PROM 프로그래머를 사용하여 이진 정보를 전기적으로 한 번 프로그래밍 할 수있는 유연성이 있습니다.
PROM은 고정 AND 어레이 및 프로그래밍 가능 OR 어레이를 가진 프로그래밍 가능한 논리 장치입니다. 그만큼block diagram PROM의 내용은 다음 그림과 같습니다.

여기서 AND 게이트의 입력은 프로그래밍 가능한 유형이 아닙니다. 따라서 각각 n 개의 입력을 갖는 2n 개의 AND 게이트를 사용하여 2n 개의 제품 항 을 생성해야합니다 . nx2 n 디코더 를 사용하여 이러한 제품 용어를 구현할 수 있습니다 . 따라서이 디코더는 'n'을 생성합니다.min terms.
여기서 OR 게이트의 입력은 프로그래밍 할 수 있습니다. 즉, AND 게이트의 모든 출력이 각 OR 게이트에 입력으로 적용되기 때문에 필요한 제품 용어를 원하는만큼 프로그래밍 할 수 있습니다. 따라서 PROM의 출력은 다음과 같은 형식이됩니다.sum of min terms.
예
다음을 구현하겠습니다. Boolean functions PROM 사용.
$$ A (X, Y, Z) = \ sum m \ left (5,6,7 \ right) $$
$$ B (X, Y, Z) = \ sum m \ left (3,5,6,7 \ right) $$
주어진 두 함수는 최소 용어 형식의 합계이며 각 함수에는 세 개의 변수 X, Y 및 Z가 있습니다. 따라서이 두 함수를 생성하려면 3-8 디코더와 두 개의 프로그래밍 가능한 OR 게이트가 필요합니다. 해당PROM 다음 그림에 나와 있습니다.

여기서 3 ~ 8 개의 디코더는 8 개의 최소 항을 생성합니다. 두 개의 프로그래밍 가능한 OR 게이트는 이러한 모든 최소 용어에 액세스 할 수 있습니다. 그러나 각 OR 게이트에 의해 각각의 부울 함수를 생성하기 위해 필요한 최소 항만 프로그래밍됩니다. 기호 'X'는 프로그래밍 가능한 연결에 사용됩니다.
프로그래밍 가능 어레이 로직 (PAL)
PAL은 Programmable AND array & fixed OR array를 가진 프로그램 가능한 논리 장치입니다. PAL의 장점은 프로그래밍 가능한 AND 게이트를 사용하여 모든 최소 항을 생성하는 대신 부울 함수의 필수 제품 항만 생성 할 수 있다는 것입니다. 그만큼block diagram PAL의 값은 다음 그림과 같습니다.

여기서 AND 게이트의 입력은 프로그래밍 할 수 있습니다. 즉, 각 AND 게이트에는 정상 및 보완 변수 입력이 모두 있습니다. 따라서 요구 사항에 따라 이러한 입력을 프로그래밍 할 수 있습니다. 따라서 필요한 항목 만 생성 할 수 있습니다.product terms 이 AND 게이트를 사용하여.
여기서 OR 게이트의 입력은 프로그래밍 가능한 유형이 아닙니다. 따라서 각 OR 게이트에 대한 입력 수는 고정 유형입니다. 따라서 각 OR 게이트에 필요한 제품 용어를 입력으로 적용하십시오. 따라서 PAL의 출력은 다음과 같은 형식이됩니다.sum of products form.
예
다음을 구현하겠습니다. Boolean functions PAL 사용.
$$ A = XY + X {Z} '$$
$$ A = X {Y} '+ Y {Z}'$$
주어진 두 기능은 제품 형태의 합계입니다. 각 부울 함수에는 두 가지 제품 용어가 있습니다. 따라서이 두 함수를 생성하려면 프로그래밍 가능한 AND 게이트 4 개와 고정 OR 게이트 2 개가 필요합니다. 해당PAL 다음 그림에 나와 있습니다.

그만큼 programmable AND gates변수의 정상 및 보완 입력 모두에 액세스 할 수 있습니다. 위 그림에서 입력 X, $ {X} '$, Y, $ {Y}'$, Z & $ {Z} '$는 각 AND 게이트의 입력에서 사용할 수 있습니다. 따라서 각 AND 게이트별로 하나의 제품 용어를 생성하기 위해 필요한 리터럴 만 프로그래밍하십시오. 기호 'X'는 프로그래밍 가능한 연결에 사용됩니다.
여기서 OR 게이트의 입력은 고정 된 유형입니다. 따라서 필요한 제품 용어는 각각의 입력에 연결됩니다.OR gate. 따라서 OR 게이트는 각각의 부울 함수를 생성합니다. 상징물 '.' 고정 연결에 사용됩니다.
프로그래밍 가능 논리 어레이 (PLA)
PLA는 Programmable AND array & Programmable OR array를 모두 갖춘 프로그래밍 가능한 논리 장치입니다. 따라서 가장 유연한 PLD입니다. 그만큼block diagram PLA의 내용은 다음 그림과 같습니다.

여기서 AND 게이트의 입력은 프로그래밍 할 수 있습니다. 즉, 각 AND 게이트에는 정상 및 보완 변수 입력이 모두 있습니다. 따라서 요구 사항에 따라 이러한 입력을 프로그래밍 할 수 있습니다. 따라서 필요한 항목 만 생성 할 수 있습니다.product terms 이 AND 게이트를 사용하여.
여기에서 OR 게이트의 입력도 프로그래밍 할 수 있습니다. 따라서 AND 게이트의 모든 출력이 각 OR 게이트에 입력으로 적용되므로 필요한 제품 용어를 원하는만큼 프로그래밍 할 수 있습니다. 따라서 PAL의 출력은 다음과 같은 형식이됩니다.sum of products form.
예
다음을 구현하겠습니다. Boolean functions PLA 사용.
$$ A = XY + X {Z} '$$
$$ B = X {Y} '+ YZ + X {Z}'$$
주어진 두 기능은 제품 형태의 합계입니다. 주어진 부울 함수 A와 B에있는 제품 용어의 수는 각각 2 개와 3 개입니다. 하나의 제품 용어 인 $ {Z} 'X $는 각 기능에서 공통입니다.
따라서이 두 함수를 생성하려면 프로그래밍 가능한 AND 게이트 4 개와 프로그래밍 가능한 OR 게이트 2 개가 필요합니다. 해당PLA 다음 그림에 나와 있습니다.
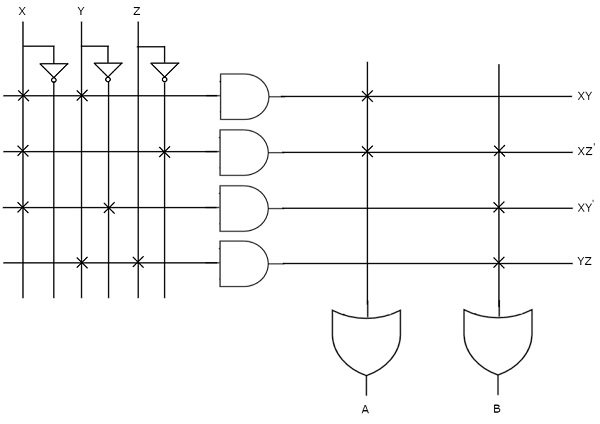
그만큼 programmable AND gates변수의 정상 및 보완 입력 모두에 액세스 할 수 있습니다. 위 그림에서 입력 X, $ {X} '$, Y, $ {Y}'$, Z & $ {Z} '$는 각 AND 게이트의 입력에서 사용할 수 있습니다. 따라서 각 AND 게이트별로 하나의 제품 용어를 생성하기 위해 필요한 리터럴 만 프로그래밍하십시오.
이러한 모든 제품 용어는 각각의 입력에서 사용할 수 있습니다. programmable OR gate. 그러나 각 OR 게이트에서 각각의 부울 함수를 생성하기 위해 필요한 제품 용어 만 프로그래밍하십시오. 기호 'X'는 프로그래밍 가능한 연결에 사용됩니다.