디지털 회로-퀵 가이드
숫자 체계의 기수 또는 기수가 'r'이면 해당 숫자 체계에있는 숫자의 범위는 0에서 r-1까지입니다. 그 숫자 체계에 존재하는 총 숫자는 'r'입니다. 그래서 우리는 2보다 크거나 같은 기수 값을 선택함으로써 다양한 수 체계를 얻을 것입니다.
이 장에서는 popular number systems각 숫자 체계에서 숫자를 표현하는 방법. 다음 숫자 체계가 가장 일반적으로 사용됩니다.
- 십진수 체계
- 이진수 시스템
- 8 진법
- 16 진수 시스템
십진수 체계
그만큼 base 또는 십진수 체계의 기수는 10. 따라서이 숫자 체계에는 0에서 9까지의 숫자가 사용됩니다. 왼쪽에있는 숫자 부분decimal point정수 부분으로 알려져 있습니다. 마찬가지로 소수점 오른쪽에있는 숫자 부분을 분수 부분이라고합니다.
이 숫자 체계에서 10 0 , 10 1 , 10 2 , 10 3 등의 가중치를 갖는 소수점 왼쪽의 연속 위치 입니다. 마찬가지로 소수점 오른쪽의 연속 된 위치는 가중치가 10-1 , 10 -2 , 10 -3 등입니다. 즉, 각 위치에는 특정 가중치가 있습니다.power of base 10
예
고려하다 decimal number 1358.246. 이 숫자의 정수 부분은 1358이고이 숫자의 소수 부분은 0.246입니다. 숫자 8, 5, 3 및 1의 가중치는 각각 100, 101, 10 2 및 10 3 입니다. 마찬가지로 숫자 2, 4 및 6의 가중치는 각각 10-1 , 10-2 및 10-3 입니다.
Mathematically, 우리는 그것을 다음과 같이 쓸 수 있습니다.
1358.246 = (1 × 3 ) + (3 × 10 2 ) + (5 × 10 1 ) + (8 × 10 0 ) + (2 × 10 -1 ) +
(4 × 10-2 ) + (6 × 10-3 )
우변 용어를 단순화 한 후 왼쪽에있는 십진수를 얻습니다.
이진수 시스템
모든 디지털 회로와 시스템은이 2 진수 시스템을 사용합니다. 그만큼base 또는이 숫자 체계의 기수는 2. 따라서 숫자 0과 1이이 숫자 체계에서 사용됩니다.
숫자의 왼쪽에있는 부분 binary point정수 부분으로 알려져 있습니다. 마찬가지로 이진수의 오른쪽에있는 숫자 부분을 분수 부분이라고합니다.
이 숫자 체계에서 가중치가 2 0 , 2 1 , 2 2 , 2 3 등인 이진 점의 왼쪽에있는 연속 위치 입니다. 마찬가지로 가중치가 2 -1 , 2 -2 , 2 -3 등인 이진 점 오른쪽의 연속 위치 . 즉, 각 위치에는 특정 가중치가 있습니다.power of base 2.
예
고려하다 binary number 1101.011. 이 숫자의 정수 부분은 1101이고이 숫자의 소수 부분은 0.011입니다. 정수 부분의 숫자 1, 0, 1 및 1의 가중치는 각각 2 0 , 2 1 , 2 2 , 2 3 입니다. 마찬가지로, 숫자 0, 1, 소수부 1 (2)의 무게가 -1 2 -2 , 2 -3 각각있다.
Mathematically, 우리는 그것을 다음과 같이 쓸 수 있습니다.
1101.011 = (1 × 2 3 ) + (1 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 ) + (0 × 2 -1 ) +
(1 × 2 -2 ) + (1 × 2 -3 )
우변 용어를 단순화 한 후, 좌변의 이진수에 해당하는 십진수를 얻게됩니다.
8 진법
그만큼 base 또는 8 진수 체계의 기수는 8. 따라서이 숫자 체계에서는 0에서 7까지의 숫자가 사용됩니다. 왼쪽에있는 숫자 부분octal point정수 부분으로 알려져 있습니다. 마찬가지로 8 진점 오른쪽에있는 숫자 부분을 분수 부분이라고합니다.
이 숫자 체계에서 8 0 , 8 1 , 8 2 , 8 3 등의 가중치를 갖는 8 진수 점 왼쪽의 연속 위치 입니다. 마찬가지로 8 -1 , 8 -2 , 8 -3 등의 가중치를 갖는 8 진점 오른쪽의 연속 위치 . 즉, 각 위치에는 특정 가중치가 있습니다.power of base 8.
예
고려하다 octal number 1457.236. 이 숫자의 정수 부분은 1457이고이 숫자의 소수 부분은 0.236입니다. 숫자 7, 5, 4, 1 (8)의 가중치가 0 8 1 8 2 8 3 에 각각있다. 마찬가지로, 숫자 2, 3, 6 (8)의 무게가 -1 8 -2 , 8 -3 각각있다.
Mathematically, 우리는 그것을 다음과 같이 쓸 수 있습니다.
1457.236 = (1 × 8 3 ) + (4 × 8 2 ) + (5 × 8 1 ) + (7 × 8 0 ) + (2 × 8 -1 ) +
(3 × 8-2 ) + (6 × 8-3 )
우변 용어를 단순화 한 후, 우리는 좌변의 8 진수에 해당하는 십진수를 얻게됩니다.
16 진수 시스템
그만큼 base 또는 Hexa-decimal number 체계의 기수는 16. 따라서 0에서 9까지의 숫자와 A에서 F까지의 문자가이 숫자 체계에서 사용됩니다. A에서 F까지의 16 진수 10 진수에 해당하는 10 진수는 10-15입니다.
숫자의 왼쪽에있는 부분 hexadecimal point정수 부분으로 알려져 있습니다. 마찬가지로 16 진수 소수점 오른쪽에있는 숫자 부분을 분수 부분이라고합니다.
이 숫자 체계에서 16 0 , 16 1 , 16 2 , 16 3 등의 가중치를 갖는 16 진수 소수점 왼쪽의 연속 위치 입니다. 마찬가지로 16 -1 , 16 -2 , 16 -3 등의 가중치를 갖는 Hexa 소수점 오른쪽의 연속 된 위치 . 즉, 각 위치에는 특정 가중치가 있습니다.power of base 16.
예
고려하다 Hexa-decimal number 1A05.2C4. 이 숫자의 정수 부분은 1A05이고이 숫자의 소수 부분은 0.2C4입니다. 숫자 5, 0, A 및 1의 가중치는 각각 16 0 , 16 1 , 16 2 및 16 3 입니다. 마찬가지로 숫자 2, C 및 4의 가중치는 각각 16-1 , 16-2 및 16-3 입니다.
Mathematically, 우리는 그것을 다음과 같이 쓸 수 있습니다.
1A05.2C4 = (1 × 16 3 ) + (10 × 16 (2) ) + (0 × 16 (1) ) + (5 × 16 0 ) + (2 × 16 -1 ) +
(12 × 16-2 ) + (4 × 16-3 )
우변 용어를 단순화 한 후 십진수를 얻습니다. 이는 왼쪽에있는 Hexa-decimal 숫자에 해당합니다.
이전 장에서 우리는 네 가지 주요 숫자 체계를 보았습니다. 이 장에서는 동등한 값을 찾기 위해 한 숫자 체계에서 다른 숫자 체계로 숫자를 변환 해 보겠습니다.
10 진수를 다른 염기로 변환
십진수에 정수 부분과 소수 부분이 모두 포함되어 있으면 십진수의 두 부분을 개별적으로 다른 밑으로 변환하십시오. 10 진수를 기본 'r'의 해당 숫자로 변환하려면 다음 단계를 따르십시오.
하다 division 소수의 정수 부분의 successive quotients기본 'r'을 사용하고 몫이 0이 될 때까지 나머지를 적어 둡니다. 등가 수의 기본 'r'의 정수 부분을 얻으려면 나머지를 역순으로 고려하십시오. 즉, 첫 번째와 마지막 나머지는 각각 최하위 숫자와 최상위 숫자를 나타냅니다.
하다 multiplication 소수의 소수 부분 및 successive fractions기본 'r'을 사용하여 결과가 0이되거나 원하는 동등한 자릿수를 얻을 때까지 캐리를 기록합니다. 동일한 수의 기본 'r'의 소수 부분을 얻기 위해 정상적인 캐리 시퀀스를 고려하십시오.
십진수를 이진으로 변환
십진수를 동등한 이진수로 변환하는 동안 다음 두 가지 유형의 연산이 발생합니다.
- 정수 부분과 연속 몫을 밑이 2로 나눕니다.
- 밑이 2 인 분수 부분과 연속 분수의 곱셈.
Example
고려하다 decimal number 58.25. 여기서 정수 부분은 58이고 소수 부분은 0.25입니다.
Step 1 − 58을 나누고 2를 밑으로하는 연속 몫.
| 조작 | 몫 | 나머지 |
|---|---|---|
| 58/2 | 29 | 0 (LSB) |
| 29/2 | 14 | 1 |
| 14/2 | 7 | 0 |
| 7/2 | 삼 | 1 |
| 3/2 | 1 | 1 |
| 1/2 | 0 | 1(MSB) |
⇒ (58) 10 = (111010) 2
따라서 integer part 동등한 이진수의 111010.
Step 2 − 0.25 곱하기와 밑이 2 인 연속 분수.
| 조작 | 결과 | 나르다 |
|---|---|---|
| 0.25 x 2 | 0.5 | 0 |
| 0.5 x 2 | 1.0 | 1 |
| - | 0.0 | - |
⇒ (.25) 10 = (.01) 2
따라서 fractional part 동등한 이진수의 .01
⇒ (58.25) 10 = (111010.01) 2
따라서 binary equivalent 십진수 58.25는 111010.01입니다.
10 진수에서 8 진수로 변환
10 진수를 동등한 8 진수로 변환하는 동안 다음 두 가지 유형의 작업이 발생합니다.
8을 밑으로하는 정수 부분과 연속 몫의 나눗셈.
8을 밑으로하는 분수 부분과 연속 분수의 곱셈.
Example
고려하다 decimal number 58.25. 여기서 정수 부분은 58이고 소수 부분은 0.25입니다.
Step 1 − 58을 나누고 8을 밑으로하는 연속 몫.
| 조작 | 몫 | 나머지 |
|---|---|---|
| 58/8 | 7 | 2 |
| 7/8 | 0 | 7 |
⇒ (58) 10 = (72) 8
따라서 integer part 동등한 8 진수는 72.
Step 2 − 0.25의 곱셈과 기수가 8 인 연속 분수.
| 조작 | 결과 | 나르다 |
|---|---|---|
| 0.25 x 8 | 2.00 | 2 |
| - | 0.00 | - |
⇒ (.25) 10 = (.2) 8
따라서 fractional part 동등한 8 진수는 .2입니다.
⇒ (58.25) 10 = (72.2) 8
따라서 octal equivalent 십진수 58.25는 72.2입니다.
10 진수에서 16 진수로 변환
10 진수를 해당하는 16 진수로 변환하는 동안 다음 두 가지 유형의 작업이 발생합니다.
- 16을 밑으로하는 정수 부분과 연속 몫의 나눗셈.
- 16을 밑으로하는 분수 부분과 연속 분수의 곱셈.
Example
고려하다 decimal number 58.25. 여기서 정수 부분은 58이고 소수 부분은 0.25입니다.
Step 1 − 58을 나누고 16을 밑으로하는 연속 몫.
| 조작 | 몫 | 나머지 |
|---|---|---|
| 58/16 | 삼 | 10 = A |
| 3/16 | 0 | 삼 |
⇒ (58) 10 = (3A) 16
따라서 integer part 동등한 Hexa-decimal 숫자는 3A입니다.
Step 2 − 0.25를 곱하고 16을 밑으로하는 연속 분수.
| 조작 | 결과 | 나르다 |
|---|---|---|
| 0.25 x 16 | 4.00 | 4 |
| - | 0.00 | - |
⇒ (.25) 10 = (.4) 16
따라서 fractional part 동등한 Hexa-decimal 숫자는 .4입니다.
⇒(58.25)10 = (3A.4)16
따라서 Hexa-decimal equivalent 십진수 58.25는 3A.4입니다.
이진수를 다른 염기로 변환
숫자를 2 진수에서 10 진수로 변환하는 과정은 2 진수를 다른 밑수로 변환하는 과정과 다릅니다. 이제 이진수를 10 진수, 8 진수 및 16 진수 시스템으로 하나씩 변환하는 방법에 대해 설명하겠습니다.
2 진수에서 10 진수로 변환
이진수를 동등한 십진수로 변환하려면 먼저 이진수 비트에 각 위치 가중치를 곱한 다음 모든 제품을 더하십시오.
Example
고려하다 binary number 1101.11.
Mathematically, 우리는 그것을 다음과 같이 쓸 수 있습니다.
(1101.11) 2 = (1 × 2 3 ) + (1 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 ) + (1 × 2 -1 ) +
(1 × 2-2 )
⇒ (1101.11) 2 = 8 + 4 + 0 + 1 + 0.5 + 0.25 = 13.75
⇒ (1101.11) 2 = (13.75) 10
따라서 decimal equivalent 이진수 1101.11은 13.75입니다.
2 진에서 8 진으로 변환
우리는 2 진수와 8 진수 시스템의 밑이 각각 2와 8이라는 것을 알고 있습니다. 2 3 = 8 이므로 3 비트의 이진수는 8 진수 1 개에 해당합니다 .
이진수를 동등한 8 진수로 변환하려면 다음 두 단계를 따르십시오.
이진 점에서 시작하여 이진 점의 양쪽에 3 비트 그룹을 만듭니다. 3 비트 그룹을 만드는 동안 1 비트 또는 2 비트가 적 으면 극단에 필요한 수의 0을 포함합니다.
3 비트의 각 그룹에 해당하는 8 진수를 씁니다.
Example
고려하다 binary number 101110.01101.
Step 1 − 이진 점의 양쪽에 3 비트 그룹을 만듭니다.
101 110.011 01
여기서 이진 점의 오른쪽에는 마지막 그룹이 2 비트 만 있습니다. 따라서 3 비트 그룹으로 만들기 위해 극단에 하나의 0을 포함합니다.
⇒ 101 110.011 010
Step 2 − 각 3 비트 그룹에 해당하는 8 진수를 씁니다.
⇒ (101 110.011 010) 2 = (56.32) 8
따라서 octal equivalent 이진수 101110.01101은 56.32입니다.
2 진수에서 16 진수로 변환
2 진수와 16 진수 시스템의 밑이 각각 2와 16이라는 것을 알고 있습니다. 이진수 4 비트는 2 4 = 16이므로 16 진수 1 자리에 해당합니다 .
이진수를 해당하는 16 진수로 변환하려면 다음 두 단계를 따르십시오.
이진 점에서 시작하여 이진 점의 양쪽에 4 비트 그룹을 만듭니다. 4 비트 그룹을 만드는 동안 일부 비트가 더 적 으면 극단에 필요한 수의 0을 포함합니다.
각 4 비트 그룹에 해당하는 16 진수 10 진수를 씁니다.
Example
고려하다 binary number 101110.01101
Step 1 − 이진 점의 양쪽에 4 비트 그룹을 만듭니다.
10 1110.0110 1
여기서 첫 번째 그룹은 2 비트 만 가지고 있습니다. 따라서 4 비트 그룹으로 만들기 위해 극단에 두 개의 0을 포함합니다. 마찬가지로 마지막 그룹도 4 비트 그룹으로 만들기 위해 맨 끝에 세 개의 0을 포함합니다.
⇒ 0010 1110.0110 1000
Step 2 − 각 4 비트 그룹에 해당하는 16 진수 10 진수를 씁니다.
⇒ (0010 1110.0110 1000) 2 = (2E.68) 16
따라서 Hexa-decimal equivalent 이진수 101110.01101은 (2E.68)입니다.
8 진수를 다른 염기로 변환
숫자를 8 진수에서 10 진수로 변환하는 프로세스는 8 진수를 다른 밑으로 변환하는 프로세스와 다릅니다. 이제 8 진수를 10 진수, 2 진수 및 16 진수 시스템으로 하나씩 변환하는 방법에 대해 설명하겠습니다.
8 진수에서 10 진수로 변환
8 진수를 동등한 10 진수로 변환하려면 먼저 8 진수의 자릿수에 각 위치 가중치를 곱한 다음 모든 제품을 더합니다.
Example
고려하다 octal number 145.23.
Mathematically, 우리는 그것을 다음과 같이 쓸 수 있습니다.
(145.23) (8) = (1 × 8 2 ) + (4 × 8 1 ) + (5 × 8 0 ) + (2 × 8 -1 ) + (3 × 8 -2 )
⇒ (145.23) 8 = 64 + 32 + 5 + 0.25 + 0.05 = 101.3
⇒ (145.23) 8 = (101.3) 10
따라서 decimal equivalent 8 진수 145.23은 101.3입니다.
8 진법에서 이진법으로 변환
8 진수를 동등한 2 진수로 변환하는 과정은 2 진수에서 8 진수로 변환하는 과정과 정반대입니다. 각 8 진수를 3 비트로 나타내면 동등한 이진수를 얻을 수 있습니다.
Example
고려하다 octal number 145.23.
각 8 진수를 3 비트로 나타냅니다.
(145.23) 8 = (001100 101.010 011) 2
값은 극단에있는 0을 제거해도 변경되지 않습니다.
⇒ (145.23) 8 = (1100101.010011) 2
따라서 binary equivalent 8 진수 145.23은 1100101.010011입니다.
8 진수에서 16 진수로 변환
8 진수를 해당하는 16 진수로 변환하려면 다음 두 단계를 따르십시오.
- 8 진수를 동등한 이진수로 변환합니다.
- 위의 이진수를 해당하는 Hexa-decimal 숫자로 변환합니다.
Example
고려하다 octal number 145.23
이전 예에서는 8 진수 145.23에 해당하는 이진 값을 1100101.010011로 얻었습니다.
바이너리에서 16 진수로 변환하는 절차를 따르면
(1100101.010011) 2 = (65.4C) 16
⇒ (145.23) 8 = (65.4C) 16
따라서 Hexa-decimal equivalent8 진수 145.23은 65.4 C 입니다.
16 진수를 다른 염기로 변환
Hexa-decimal에서 10 진수로 숫자를 변환하는 과정은 Hexa-decimal 숫자를 다른 밑수로 변환하는 과정과 다릅니다. 이제 Hexa-decimal 숫자를 10 진수, 2 진수 및 8 진수 시스템으로 하나씩 변환하는 방법에 대해 설명하겠습니다.
16 진수에서 10 진수로 변환
Hexa-decimal 숫자를 동등한 십진수로 변환하려면 먼저 Hexa-decimal 숫자의 자릿수에 각 위치 가중치를 곱한 다음 모든 제품을 더합니다.
Example
고려하다 Hexa-decimal number 1A5.2
Mathematically, 우리는 그것을 다음과 같이 쓸 수 있습니다.
(1A5.2) 16 = (1 × 16 2 ) + (10 × 16 (1) ) + (5 × 16 0 ) + (2 × 16 -1 )
⇒ (1A5.2) 16 = 256 + 160 + 5 + 0.125 = 421.125
⇒ (1A5.2) 16 = (421.125) 10
따라서 decimal equivalent 16 진수 1A5.2의 값은 421.125입니다.
Hexa-Decimal에서 이진 변환
Hexa-decimal 숫자를 동등한 이진수로 변환하는 과정은 이진수에서 Hexa-decimal로 변환하는 과정과 정반대입니다. 각 Hexa-decimal 숫자를 4 비트로 나타내면 동등한 이진수를 얻을 수 있습니다.
Example
고려하다 Hexa-decimal number 65.4C
각 16 진수 10 진수를 4 비트로 나타냅니다.
(65.4C) 6 = (0110 0101.0100 1100) 2
두 극단에있는 0을 제거해도 값은 변경되지 않습니다.
⇒ (65.4C) 16 = (1100101.010011) 2
따라서 binary equivalent Hexa-decimal number 65.4C의 1100101.010011입니다.
16 진수에서 8 진수로 변환
Hexa-decimal 숫자를 동등한 8 진수로 변환하려면 다음 두 단계를 따르십시오.
- 16 진수 10 진수를 동등한 2 진수로 변환합니다.
- 위의 이진수를 동등한 8 진수로 변환합니다.
Example
고려하다 Hexa-decimal number 65.4C
이전 예에서는 Hexa-decimal 숫자 65.4C에 해당하는 이진법을 1100101.010011로 얻었습니다.
2 진수에서 8 진수로 변환하는 절차를 따르면
(1100101.010011) 2 = (145.23) 8
⇒ (65.4C) 16 = (145.23)
따라서 octal equivalentHexa-decimal 숫자 65.4 C의 145.23입니다.
이진수를 다음 두 그룹으로 만들 수 있습니다. Unsigned numbers 과 Signed numbers.
부호없는 숫자
부호없는 숫자는 숫자의 크기 만 포함합니다. 표지판이 없습니다. 즉, 부호없는 이진수는 모두 양수입니다. 십진수 시스템에서와 같이, 숫자 앞에 양수 부호를 배치하는 것은 양수를 나타내는 선택 사항입니다. 따라서 숫자 앞에 양수 부호가 지정되지 않은 경우 0을 포함한 모든 양수는 부호없는 숫자로 처리 될 수 있습니다.
부호있는 숫자
부호있는 숫자에는 부호와 숫자 크기가 모두 포함됩니다. 일반적으로 기호는 숫자 앞에 배치됩니다. 그래서 우리는 양수의 양의 부호와 음의 음의 부호를 고려해야합니다. 따라서 해당 부호가 숫자 앞에 할당되면 모든 숫자를 부호있는 숫자로 취급 할 수 있습니다.
부호 비트가 0이면 이진수가 양수임을 나타냅니다. 마찬가지로 부호 비트가 1이면 이진수가 음수임을 나타냅니다.
부호없는 이진수의 표현
부호없는 이진수에있는 비트는 magnitude숫자의. 즉, 부호없는 이진수에‘N’ 비트, 다음 모두 N 비트는 부호 비트가 없기 때문에 숫자의 크기를 나타냅니다.
Example
고려하다 decimal number 108. 이 숫자에 해당하는 이진수는 다음과 같습니다.1101100. 이것은 부호없는 이진수의 표현입니다.
(108) 10 = (1101100) 2
7 비트가 있습니다. 이 7 비트는 숫자 108의 크기를 나타냅니다.
부호있는 이진 숫자의 표현
부호있는 이진수의 MSB (Most Significant Bit)는 숫자의 부호를 나타내는 데 사용됩니다. 따라서sign bit. 양수 부호는 부호 비트에 '0'을 배치하여 표시됩니다. 마찬가지로 음수 부호는 부호 비트에 '1'을 배치하여 표시됩니다.
부호있는 이진수에 'N'비트가 포함 된 경우 (N-1) 비트는 숫자의 부호를 나타내는 데 1 비트 (MSB)가 예약되어 있으므로 숫자의 크기 만 나타냅니다.
세 가지가 있습니다 types of representations 부호있는 이진수
- Sign-Magnitude 형식
- 1의 보수 형태
- 2의 보수 형태
이 세 가지 형식 모두에서 양수의 표현은 동일합니다. 그러나 음수의 표현 만 각 형식에서 다릅니다.
Example
고려하다 positive decimal number +108. 이 숫자의 크기에 해당하는 이진수는 1101100입니다.이 7 비트는 숫자 108의 크기를 나타냅니다. 양수이므로 부호 비트는 크기의 가장 왼쪽에있는 0으로 간주합니다.
(+108) 10 = (01101100) 2
따라서 signed binary representation양의 십진수 +108은. 따라서 동일한 표현이 부호 크기 형식, 1의 보수 형식 및 양의 십진수 +108에 대한 2의 보수 형식에서 유효합니다.
Sign-Magnitude 형식
부호 크기 형식에서 MSB는 다음을 나타내는 데 사용됩니다. sign 숫자의 나머지 비트는 magnitude번호의. 따라서 부호없는 이진수의 가장 왼쪽에 부호 비트를 포함하십시오. 이 표현은 부호있는 십진수 표현과 유사합니다.
Example
고려하다 negative decimal number -108. 이 숫자의 크기는 108입니다. 108의 부호없는 이진 표현은 1101100입니다. 이것은 7 비트입니다. 이 모든 비트는 크기를 나타냅니다.
주어진 숫자가 음수이므로 부호 비트는 크기의 가장 왼쪽에있는 1로 간주하십시오.
(−108) 10 = (11101100) 2
따라서 -108의 부호 크기 표현은 다음과 같습니다. 11101100.
1의 보수 형태
숫자의 1의 보수는 다음과 같이 구합니다. complementing all the bits부호있는 이진수의. 따라서 1의 양수 보수는 음수를 제공합니다. 마찬가지로 음수의 1의 보수는 양수를 제공합니다.
즉, 부호 비트를 포함하여 이진수의 2 곱하기 1의 보수를 수행하면 원래의 부호있는 이진수를 얻게됩니다.
Example
고려하다 negative decimal number -108. 이 숫자의 크기는 108입니다. 108의 부호있는 이진 표현은 01101100입니다.
그것은 8 비트를 가지고 있습니다. 이 숫자의 MSB는 0이며 양수를 나타냅니다. 0의 보완은 1이고 그 반대의 경우도 마찬가지입니다. 따라서 음수를 얻으려면 0을 1로, 1을 0으로 바꾸십시오.
(−108) 10 = (10010011) 2
따라서 1’s complement of (108)10 이다 (10010011)2.
2의 보수 형태
이진수의 2의 보수는 다음과 같이 구합니다. adding one to the 1’s complement부호있는 이진수의. 따라서 양수의 2의 보수는 음수를 제공합니다. 마찬가지로 음수의 2의 보수는 양수를 제공합니다.
즉, 부호 비트를 포함하여 이진수의 2 곱하기 2의 보수를 수행하면 원래의 부호있는 이진수를 얻게됩니다.
Example
고려하다 negative decimal number -108.
우리는 (108)10 이다 (10010011)2
2의 (108) 10 칭찬 = 1의 (108) 10 + 1 칭찬
= 10010011 + 1
= 10010100
따라서 2’s complement of (108)10 이다 (10010100)2.
이 장에서는 2의 보수 방법을 사용하여 부호있는 두 이진수에 대해 수행 할 수있는 기본적인 산술 연산에 대해 설명하겠습니다. 그만큼basic arithmetic operations 더하기와 빼기입니다.
두 개의 부호있는 이진수 더하기
2의 보수 형식으로 표시되는 두 개의 부호있는 이진수 A와 B를 고려하십시오. 우리는addition두 개의 부호없는 이진수를 더한 것과 비슷합니다. 그러나 결과 합계에 부호 비트에서 수행 된 작업이 포함 된 경우 올바른 값을 얻기 위해이를 무시 (무시)합니다.
결과 합계가 양수이면 그 크기를 직접 찾을 수 있습니다. 그러나 결과 합이 음수이면 크기를 얻기 위해 2의 보수를 취하십시오.
예 1
우리가 수행하자 addition 두 십진수 +7 and +4 2의 보수 방법을 사용합니다.
그만큼 2’s complement 각각 5 비트가있는 +7 및 +4의 표현이 아래에 나와 있습니다.
(+7) 10 = (00111) 2
(+4) 10 = (00100) 2
이 두 숫자를 더하면
(+7) 10 + (+ 4) 10 = (00111) 2 + (00100) 2
⇒ (+7) 10 + (+ 4) 10 = (01011) 2 .
결과 합계에는 5 비트가 포함됩니다. 따라서 부호 비트에서 수행되지 않습니다. 부호 비트 '0'은 결과 합계가positive. 따라서 합계의 크기는 십진수 체계에서 11입니다. 따라서 두 개의 양수를 더하면 또 다른 양수가됩니다.
예 2
우리가 수행하자 addition 두 십진수 -7 과 -4 2의 보수 방법을 사용합니다.
그만큼 2’s complement 각각 5 비트가있는 -7 및 -4의 표현이 아래에 나와 있습니다.
(−7) 10 = (11001) 2
(−4) 10 = (11100) 2
이 두 숫자를 더하면
(−7) 10 + (−4) 10 = (11001) 2 + (11100) 2
⇒ (−7) 10 + (−4) 10 = (110101) 2 .
결과 합계에는 6 비트가 포함됩니다. 이 경우 캐리는 부호 비트에서 얻습니다. 그래서 우리는 그것을 제거 할 수 있습니다
캐리를 제거한 후의 결과 합계는 (−7) 10 + (−4) 10 =(10101)2.
부호 비트 '1'은 결과 합계가 negative. 따라서 2의 보수를 취함으로써 10 진수 시스템에서 결과 합의 크기를 11로 얻을 수 있습니다. 따라서 두 개의 음수를 더하면 또 다른 음수가됩니다.
두 개의 부호있는 이진수 빼기
2의 보수 형식으로 표시되는 두 개의 부호있는 이진수 A와 B를 고려하십시오. 우리는 양수의 2의 보수가 음수를 제공한다는 것을 알고 있습니다. 그래서 우리가 숫자 A에서 숫자 B를 빼야 할 때마다 B의 2의 보수를 A에 더합니다. 그래서,mathematically 우리는 그것을 다음과 같이 쓸 수 있습니다.
A - B = A + (2's complement of B)
비슷하게, 우리가 숫자 B에서 숫자 A를 빼야한다면, A의 2의 보수를 B에 더하세요. 그래서, mathematically 우리는 그것을 다음과 같이 쓸 수 있습니다.
B - A = B + (2's complement of A)
따라서 두 개의 부호있는 이진수를 빼는 것은 두 개의 부호있는 이진수를 더하는 것과 비슷합니다. 그러나, 우리는 빼야하는 숫자의 2의 보수를 취해야합니다. 이것이advantage2의 보수 기법의. 두 개의 부호있는 이진수를 더하는 동일한 규칙을 따르십시오.
예제 3
우리가 수행하자 subtraction 두 십진수 +7 and +4 2의 보수 방법을 사용합니다.
이 두 숫자를 빼면
(+7) 10 − (+4) 10 = (+7) 10 + (−4) 10 .
그만큼 2’s complement 각각 5 비트로 +7 및 -4의 표현이 아래에 나와 있습니다.
(+7) 10 = (00111) 2
(+4) 10 = (11100) 2
⇒ (+7) 10 + (+4) 10 = (00111) 2 + (11100) 2 = (00011) 2
여기서는 부호 비트에서 얻은 캐리입니다. 그래서 우리는 그것을 제거 할 수 있습니다. 캐리 제거 후 결과 합계는 다음과 같습니다.
(+7) 10 + (+4) 10 =(00011)2
부호 비트 '0'은 결과 합계가 positive. 따라서 그 크기는 십진수 체계에서 3입니다. 따라서 두 십진수 +7과 +4를 빼면 +3이됩니다.
예 4
우리가 수행하자 subtraction of 두 개의 십진수 +4 과 +7 2의 보수 방법을 사용합니다.
이 두 숫자를 빼면
(+4) 10 − (+7) 10 = (+4) 10 + (−7) 10 .
그만큼 2’s complement 각각 5 비트로 +4 및 -7의 표현이 아래에 나와 있습니다.
(+4) 10 = (00100) 2
(-7) 10 = (11001) 2
⇒ (+4) 10 + (-7) 10 = (00100) 2 + (11001) 2 = (11101) 2
여기서 캐리는 부호 비트에서 얻지 않습니다. 부호 비트 '1'은 결과 합계가negative. 따라서 2의 보수를 취함으로써 10 진수 시스템에서 결과 합계의 크기를 3으로 얻습니다. 따라서 두 개의 십진수 +4와 +7을 빼면 -3이됩니다.
코딩에서 숫자 또는 문자가 특정 기호 그룹으로 표시되면 숫자 또는 문자가 인코딩되고 있다고합니다. 기호 그룹은 다음과 같이 호출됩니다.code. 디지털 데이터는 비트 그룹으로 표현, 저장 및 전송됩니다. 이 비트 그룹은binary code.
이진 코드는 두 가지 유형으로 분류 할 수 있습니다.
- 가중 코드
- 가중치가없는 코드
코드에 위치 가중치가있는 경우 weighted code. 그렇지 않으면 가중치가없는 코드입니다. 가중치 코드는 양의 가중치 코드와 음의 가중치 코드로 더 분류 될 수 있습니다.
십진수에 대한 이진 코드
다음 표는 10 진수 0에서 9까지의 다양한 이진 코드를 보여줍니다.
| 십진수 | 8421 코드 | 2421 코드 | 84-2-1 코드 | 초과 3 코드 |
|---|---|---|---|---|
| 0 | 0000 | 0000 | 0000 | 0011 |
| 1 | 0001 | 0001 | 0111 | 0100 |
| 2 | 0010 | 0010 | 0110 | 0101 |
| 삼 | 0011 | 0011 | 0101 | 0110 |
| 4 | 0100 | 0100 | 0100 | 0111 |
| 5 | 0101 | 1011 | 1011 | 1000 |
| 6 | 0110 | 1100 년 | 1010 년 | 1001 |
| 7 | 0111 | 1101 | 1001 | 1010 년 |
| 8 | 1000 | 1110 년 | 1000 | 1011 |
| 9 | 1001 | 1111 년 | 1111 년 | 1100 년 |
10 진수 체계로 10 자리 숫자가 있습니다. 이 10 자리 숫자를 이진수로 나타내려면 최소 4 비트가 필요합니다. 그러나 4 비트에는 0과 1의 고유 한 16 개의 조합이 있습니다. 10 진수 10 자리 만 있기 때문에 다른 6 개의 0과 1 조합은 필요하지 않습니다.
8 4 2 1 코드
이 코드의 가중치는 8, 4, 2 및 1입니다.
이 코드에는 모두 양의 가중치가 있습니다. 그래서, 그것은positively weighted code.
이 코드는 natural BCD (이진 코드 십진수) code.
Example
10 진수 786에 해당하는 BCD를 찾아 보겠습니다.이 숫자는 3 자리 10 진수 7, 8, 6입니다. 표에서 7, 8, 6의 BCD (8421) 코드는 각각 0111, 1000 및 0110입니다. .
∴ (786)10 = (011110000110)BCD
10 진수의 각 BCD 코드에는 4 비트가 있으므로 BCD 표현에는 12 비트가 있습니다.
2 4 2 1 코드
이 코드의 가중치는 2, 4, 2 및 1입니다.
이 코드에는 모두 양의 가중치가 있습니다. 그래서, 그것은positively weighted code.
이것은 unnatural BCD암호. 부 자연스러운 BCD 코드의 가중치 합계는 9입니다.
이것은 self-complementing암호. 자체 보완 코드는 동등한 2421 표현에서 1과 0을 교환하여 10 진수의 9의 보수를 제공합니다.
Example
십진수 786에 해당하는 2421을 찾으십시오.이 숫자는 3 개의 십진수 7, 8 및 6을 갖습니다. 표에서 7, 8 및 6의 2421 코드는 각각 1101, 1110 및 1100입니다.
따라서 10 진수 786에 해당하는 2421은 다음과 같습니다. 110111101100.
8 4 -2 -1 코드
이 코드의 가중치는 8, 4, -2 및 -1입니다.
이 코드에는 양의 가중치와 함께 음의 가중치가 있습니다. 그래서, 그것은negatively weighted code.
이것은 unnatural BCD 암호.
이것은 self-complementing 암호.
Example
10 진수 786에 해당하는 8 4-2-1을 찾습니다.이 숫자는 3 개의 10 진수 7, 8 및 6을 가지고 있습니다. 표에서 7, 8 및 6의 8 4 -2 -1 코드를 작성할 수 있습니다. 각각 1001, 1000 및 1010입니다.
따라서 10 진수 786에 해당하는 8 4 -2 -1은 다음과 같습니다. 100110001010.
초과 3 코드
이 코드에는 가중치가 없습니다. 그래서, 그것은un-weighted code.
10 진수에 해당하는 이진수에 3 (0011)을 더하여 10 진수의 Excess 3 코드를 얻습니다. 따라서이를 Excess 3 코드라고합니다.
이것은 self-complementing 암호.
Example
10 진수 786에 해당하는 Excess 3을 찾으십시오.이 숫자는 3 개의 10 진수 7, 8 및 6을 갖습니다. 표에서 7, 8 및 6의 Excess 3 코드를 각각 1010, 1011 및 1001로 작성할 수 있습니다.
따라서 10 진수 786에 해당하는 Excess 3은 다음과 같습니다. 101010111001
그레이 코드
다음 표는 각 4 비트 바이너리 코드에 해당하는 4 비트 그레이 코드를 보여줍니다.
| 십진수 | 바이너리 코드 | 그레이 코드 |
|---|---|---|
| 0 | 0000 | 0000 |
| 1 | 0001 | 0001 |
| 2 | 0010 | 0011 |
| 삼 | 0011 | 0010 |
| 4 | 0100 | 0110 |
| 5 | 0101 | 0111 |
| 6 | 0110 | 0101 |
| 7 | 0111 | 0100 |
| 8 | 1000 | 1100 년 |
| 9 | 1001 | 1101 |
| 10 | 1010 년 | 1111 년 |
| 11 | 1011 | 1110 년 |
| 12 | 1100 년 | 1010 년 |
| 13 | 1101 | 1011 |
| 14 | 1110 년 | 1001 |
| 15 | 1111 년 | 1000 |
이 코드에는 가중치가 없습니다. 그래서, 그것은un-weighted code.
위의 표에서 연속적인 Gray 코드는 한 비트 위치에서만 다릅니다. 따라서이 코드는 다음과 같이 호출됩니다.unit distance 암호.
바이너리 코드를 그레이 코드로 변환
이진 코드를 동등한 그레이 코드로 변환하려면 다음 단계를 따르십시오.
주어진 이진 코드를 고려하고 MSB 왼쪽에 0을 배치합니다.
0부터 시작하여 연속 된 두 비트를 비교합니다. 2 비트가 같으면 출력은 0입니다. 그렇지 않으면 출력은 1입니다.
그레이 코드의 LSB를 얻을 때까지 위의 단계를 반복합니다.
Example
표에서 이진 코드 1000에 해당하는 Gray 코드가 1100임을 알 수 있습니다. 이제 위의 절차를 사용하여 확인하겠습니다.
이진 코드는 1000입니다.
Step 1 − MSB 왼쪽에 0을 배치하면 바이너리 코드는 01000이됩니다.
Step 2 − 연속적인 2 비트의 새로운 바이너리 코드를 비교하여 다음과 같은 회색 코드를 얻을 수 있습니다. 1100.
우리는 비트 0과 1이 두 개의 다른 아날로그 전압 범위에 해당한다는 것을 알고 있습니다. 따라서 한 시스템에서 다른 시스템으로 이진 데이터를 전송하는 동안 노이즈도 추가 될 수 있습니다. 이로 인해 다른 시스템에서 수신 된 데이터에 오류가있을 수 있습니다.
이는 비트 0이 1로 변경되거나 비트 1이 0으로 변경 될 수 있음을 의미합니다. 우리는 잡음의 간섭을 피할 수 없습니다. 그러나 먼저 오류가 있는지 여부를 감지 한 다음 해당 오류를 수정하여 원래 데이터를 다시 가져올 수 있습니다. 이를 위해 다음 코드를 사용할 수 있습니다.
- 오류 감지 코드
- 오류 수정 코드
Error detection codes− 수신 된 데이터 (비트 스트림)에 존재하는 오류를 감지하는 데 사용됩니다. 이러한 코드에는 원본 비트 스트림에 포함 (추가)되는 일부 비트가 포함됩니다. 이러한 코드는 원본 데이터 (비트 스트림) 전송 중에 발생한 오류를 감지합니다.Example − 패리티 코드, 해밍 코드.
Error correction codes− 수신 된 데이터 (비트 스트림)에 존재하는 오류를 수정하는 데 사용되어 원래 데이터를 얻습니다. 오류 수정 코드는 또한 유사한 오류 감지 코드 전략을 사용합니다.Example − 해밍 코드.
따라서 오류를 감지하고 수정하기 위해 전송시 데이터 비트에 추가 비트가 추가됩니다.
패리티 코드
MSB의 왼쪽 또는 원래 비트 스트림의 LSB 오른쪽에 하나의 패리티 비트를 포함 (추가)하는 것은 쉽습니다. 패리티 코드에는 두 가지 유형, 즉 선택한 패리티 유형에 따라 짝수 패리티 코드와 홀수 패리티 코드가 있습니다.
심지어 패리티 코드
이진 코드에 1이 짝수이면 짝수 패리티 비트의 값은 0이어야합니다. 그렇지 않으면 하나 여야합니다. 그래서, 짝수 개의 사람들이even parity code. 패리티 코드조차도 데이터 비트와 패리티 비트를 포함합니다.
다음 표는 even parity codes각 3 비트 이진 코드에 해당합니다. 여기서 짝수 패리티 비트는 바이너리 코드의 LSB 오른쪽에 포함됩니다.
| 바이너리 코드 | 심지어 패리티 비트 | 심지어 패리티 코드 |
|---|---|---|
| 000 | 0 | 0000 |
| 001 | 1 | 0011 |
| 010 | 1 | 0101 |
| 011 | 0 | 0110 |
| 100 | 1 | 1001 |
| 101 | 0 | 1010 년 |
| 110 | 0 | 1100 년 |
| 111 | 1 | 1111 년 |
여기서 짝수 패리티 코드에 존재하는 비트 수는 4입니다. 따라서이 짝수 패리티 코드에서 가능한 짝수는 0, 2, 4입니다.
다른 시스템이 이러한 짝수 패리티 코드 중 하나를 수신하면 수신 된 데이터에 오류가 없습니다. 짝수 패리티 비트 이외의 비트는 이진 코드의 비트와 동일합니다.
다른 시스템이 패리티 코드 이외의 다른 코드를 수신하면 수신 된 데이터에 오류가 발생합니다. 이 경우 오류의 비트 위치를 모르기 때문에 원래 이진 코드를 예측할 수 없습니다.
따라서 패리티 비트조차도 수신 된 패리티 코드의 오류 감지에만 유용합니다. 그러나 오류를 수정하는 것만으로는 충분하지 않습니다.
홀수 패리티 코드
바이너리 코드에 홀수의 1이있는 경우 홀수 패리티 비트의 값은 0이어야합니다. 그렇지 않으면 하나 여야합니다. 그래서, 홀수로 존재하는odd parity code. 홀수 패리티 코드에는 데이터 비트와 홀수 패리티 비트가 포함됩니다.
다음 표는 odd parity codes각 3 비트 이진 코드에 해당합니다. 여기서는 바이너리 코드의 LSB 오른쪽에 홀수 패리티 비트가 포함됩니다.
| Binary Code | Odd Parity bit | Odd Parity Code |
|---|---|---|
| 000 | 1 | 0001 |
| 001 | 0 | 0010 |
| 010 | 0 | 0100 |
| 011 | 1 | 0111 |
| 100 | 0 | 1000 |
| 101 | 1 | 1011 |
| 110 | 1 | 1101 |
| 111 | 0 | 1110 |
Here, the number of bits present in the odd parity codes is 4. So, the possible odd number of ones in these odd parity codes are 1 & 3.
If the other system receives one of these odd parity codes, then there is no error in the received data. The bits other than odd parity bit are same as that of binary code.
If the other system receives other than odd parity codes, then there is an error(s) in the received data. In this case, we can’t predict the original binary code because we don’t know the bit position(s) of error.
Therefore, odd parity bit is useful only for detection of error in the received parity code. But, it is not sufficient to correct the error.
Hamming Code
Hamming code is useful for both detection and correction of error present in the received data. This code uses multiple parity bits and we have to place these parity bits in the positions of powers of 2.
The minimum value of 'k' for which the following relation is correct (valid) is nothing but the required number of parity bits.
$$2^k\geq n+k+1$$
Where,
‘n’ is the number of bits in the binary code (information)
‘k’ is the number of parity bits
Therefore, the number of bits in the Hamming code is equal to n + k.
Let the Hamming code is $b_{n+k}b_{n+k-1}.....b_{3}b_{2}b_{1}$ & parity bits $p_{k}, p_{k-1}, ....p_{1}$. We can place the ‘k’ parity bits in powers of 2 positions only. In remaining bit positions, we can place the ‘n’ bits of binary code.
Based on requirement, we can use either even parity or odd parity while forming a Hamming code. But, the same parity technique should be used in order to find whether any error present in the received data.
Follow this procedure for finding parity bits.
Find the value of p1, based on the number of ones present in bit positions b3, b5, b7 and so on. All these bit positions (suffixes) in their equivalent binary have ‘1’ in the place value of 20.
Find the value of p2, based on the number of ones present in bit positions b3, b6, b7 and so on. All these bit positions (suffixes) in their equivalent binary have ‘1’ in the place value of 21.
Find the value of p3, based on the number of ones present in bit positions b5, b6, b7 and so on. All these bit positions (suffixes) in their equivalent binary have ‘1’ in the place value of 22.
Similarly, find other values of parity bits.
Follow this procedure for finding check bits.
Find the value of c1, based on the number of ones present in bit positions b1, b3, b5, b7 and so on. All these bit positions (suffixes) in their equivalent binary have ‘1’ in the place value of 20.
Find the value of c2, based on the number of ones present in bit positions b2, b3, b6, b7 and so on. All these bit positions (suffixes) in their equivalent binary have ‘1’ in the place value of 21.
Find the value of c3, based on the number of ones present in bit positions b4, b5, b6, b7 and so on. All these bit positions (suffixes) in their equivalent binary have ‘1’ in the place value of 22.
Similarly, find other values of check bits.
The decimal equivalent of the check bits in the received data gives the value of bit position, where the error is present. Just complement the value present in that bit position. Therefore, we will get the original binary code after removing parity bits.
Example 1
Let us find the Hamming code for binary code, d4d3d2d1 = 1000. Consider even parity bits.
The number of bits in the given binary code is n=4.
We can find the required number of parity bits by using the following mathematical relation.
$$2^k\geq n+k+1$$
Substitute, n=4 in the above mathematical relation.
$$\Rightarrow 2^k\geq 4+k+1$$
$$\Rightarrow 2^k\geq 5+k$$
The minimum value of k that satisfied the above relation is 3. Hence, we require 3 parity bits p1, p2, and p3. Therefore, the number of bits in Hamming code will be 7, since there are 4 bits in binary code and 3 parity bits. We have to place the parity bits and bits of binary code in the Hamming code as shown below.
The 7-bit Hamming code is $b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}=d_{4}d_{3}d_{2}p_{3}d_{1}p_{2}bp_{1}$
By substituting the bits of binary code, the Hamming code will be $b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1} = 100p_{3}Op_{2}p_{1}$. Now, let us find the parity bits.
$$p_{1}=b_{7}\oplus b_{5}\oplus b_{3}=1 \oplus 0 \oplus 0=1$$
$$p_{2}=b_{7}\oplus b_{6}\oplus b_{3}=1 \oplus 0 \oplus 0=1$$
$$p_{3}=b_{7}\oplus b_{6}\oplus b_{5}=1 \oplus 0 \oplus 0=1$$
By substituting these parity bits, the Hamming code will be $b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}= 1001011$.
Example 2
In the above example, we got the Hamming code as $b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}= 1001011$. Now, let us find the error position when the code received is $b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}= 1001111$.
Now, let us find the check bits.
$$c_{1}=b_{7}\oplus b_{5}\oplus b_{3}\oplus b_{1}=1 \oplus 0 \oplus 1 \oplus1 =1$$
$$c_{2}=b_{7}\oplus b_{6}\oplus b_{3}\oplus b_{2}=1 \oplus 0 \oplus 1 \oplus1 =1$$
$$c_{3}=b_{7}\oplus b_{6}\oplus b_{5}\oplus b_{4}=1 \oplus 0 \oplus 0 \oplus1 =0$$
The decimal value of check bits gives the position of error in received Hamming code.
$$c_{3}c_{2}c_{1} = \left ( 011 \right )_{2}=\left ( 3 \right )_{10}$$
Therefore, the error present in third bit (b3) of Hamming code. Just complement the value present in that bit and remove parity bits in order to get the original binary code.
Boolean Algebra is an algebra, which deals with binary numbers & binary variables. Hence, it is also called as Binary Algebra or logical Algebra. A mathematician, named George Boole had developed this algebra in 1854. The variables used in this algebra are also called as Boolean variables.
The range of voltages corresponding to Logic ‘High’ is represented with ‘1’ and the range of voltages corresponding to logic ‘Low’ is represented with ‘0’.
Postulates and Basic Laws of Boolean Algebra
In this section, let us discuss about the Boolean postulates and basic laws that are used in Boolean algebra. These are useful in minimizing Boolean functions.
Boolean Postulates
Consider the binary numbers 0 and 1, Boolean variable (x) and its complement (x’). Either the Boolean variable or complement of it is known as literal. The four possible logical OR operations among these literals and binary numbers are shown below.
x + 0 = x
x + 1 = 1
x + x = x
x + x '= 1
마찬가지로 가능한 네 가지 logical AND 이러한 리터럴과 이진수 간의 연산은 다음과 같습니다.
x.1 = x
x.0 = 0
xx = x
x.x '= 0
이것들은 단순한 부울 가정입니다. Boolean 변수를 '0'또는 '1'로 대체하여 이러한 가정을 쉽게 확인할 수 있습니다.
Note− 부울 변수의 보수는 변수 자체와 동일합니다. 즉, (x ')'= x.
부울 대수의 기본 법칙
다음은 부울 대수학의 세 가지 기본 법칙입니다.
- 교환법
- 연합 법
- 분배 법
교환법
두 부울 변수의 논리 연산이이 두 변수의 순서에 관계없이 동일한 결과를 제공하는 경우 해당 논리 연산은 다음과 같습니다. Commutative. 두 부울 변수 x 및 y의 논리적 OR 및 논리적 AND 연산은 다음과 같습니다.
x + y = y + x
xy = yx
기호 '+'는 논리 OR 연산을 나타냅니다. 마찬가지로 기호 '.' 논리적 AND 연산을 나타내며 선택 사항입니다. 교환법은 논리적 OR 및 논리적 AND 연산을 따릅니다.
연합 법
두 개의 부울 변수에 대한 논리 연산이 먼저 수행되고 나머지 변수로 동일한 연산이 수행되면 동일한 결과가 나오면 해당 논리 연산은 다음과 같습니다. Associative. 세 가지 부울 변수 x, y 및 z의 논리적 OR 및 논리적 AND 연산이 아래에 나와 있습니다.
x + (y + z) = (x + y) + z
x. (yz) = (xy) .z
연관 법은 논리적 OR 및 논리적 AND 연산을 따릅니다.
배급 법
논리 연산이 부울 함수에있는 모든 용어에 배포 될 수있는 경우 해당 논리 연산은 다음과 같습니다. Distributive. 세 가지 부울 변수 x, y 및 z의 논리적 OR 및 논리적 AND 연산의 분포는 다음과 같습니다.
x. (y + z) = xy + xz
x + (yz) = (x + y). (x + z)
분배 법은 논리적 OR 및 논리적 AND 연산을 따릅니다.
이것이 부울 대수의 기본 법칙입니다. 부울 변수를 '0'또는 '1'로 대체하여 이러한 법칙을 쉽게 확인할 수 있습니다.
부울 대수의 정리
다음 두 가지 정리가 부울 대수에 사용됩니다.
- 이중성 정리
- DeMorgan의 정리
이중성 정리
이 정리는 dual논리 AND 연산자를 논리 OR 연산자로 바꾸고 0을 1로 바꿔 부울 함수의 값을 얻습니다. 모든 부울 함수에 해당하는 이중 함수가 있습니다.
부울 가정과 기본 법칙 섹션에서 논의한 부울 방정식 (관계)을 두 그룹으로 만들어 보겠습니다. 다음 표는이 두 그룹을 보여줍니다.
| 그룹 1 | 그룹 2 |
|---|---|
| x + 0 = x | x.1 = x |
| x + 1 = 1 | x.0 = 0 |
| x + x = x | xx = x |
| x + x '= 1 | x.x '= 0 |
| x + y = y + x | xy = yx |
| x + (y + z) = (x + y) + z | x. (yz) = (xy) .z |
| x. (y + z) = xy + xz | x + (yz) = (x + y). (x + z) |
각 행에는 두 개의 부울 방정식이 있으며 서로 이중입니다. 이원성 정리를 사용하여 Group1과 Group2의 이러한 모든 부울 방정식을 확인할 수 있습니다.
DeMorgan의 정리
이 정리는 complement of Boolean function. 두 개 이상의 부울 변수의 논리 OR의 보수가 각 보완 변수의 논리 AND와 동일 함을 나타냅니다.
2 개의 부울 변수 x와 y를 갖는 DeMorgan의 정리는 다음과 같이 나타낼 수 있습니다.
(x + y) '= x'.y'
위의 Boolean 함수의 이중은
(xy) '= x'+ y '
따라서 두 부울 변수의 논리 AND의 보수는 각 보완 변수의 논리 OR과 같습니다. 마찬가지로 2 개 이상의 부울 변수에도 DeMorgan의 정리를 적용 할 수 있습니다.
부울 함수의 단순화
지금까지 우리는 부울 대수의 가정, 기본 법칙 및 정리에 대해 논의했습니다. 이제 몇 가지 부울 함수를 단순화 해 보겠습니다.
예 1
하자 simplify 부울 함수, f = p'qr + pq'r + pqr '+ pqr
이 함수는 두 가지 방법으로 단순화 할 수 있습니다.
Method 1
부울 함수가 주어지면 f = p'qr + pq'r + pqr '+ pqr입니다.
Step 1− 첫 번째 및 두 번째 항에서 r은 공통이고 세 번째 및 네 번째 항에서 pq는 공통입니다. 따라서 사용하여 일반적인 용어를 사용하십시오.Distributive law.
⇒ f = (p'q + pq ') r + pq (r'+ r)
Step 2− 첫 번째 괄호 안에있는 용어는 Ex-OR 연산으로 단순화 할 수 있습니다. 두 번째 괄호 안에있는 용어는 다음을 사용하여 '1'로 단순화 할 수 있습니다.Boolean postulate
⇒ f = (p ⊕q) r + pq (1)
Step 3− 첫 번째 용어는 더 이상 단순화 할 수 없습니다. 그러나 두 번째 항은 다음을 사용하여 pq로 단순화 할 수 있습니다.Boolean postulate.
⇒ f = (p ⊕q) r + pq
따라서 단순화 된 부울 함수는 다음과 같습니다. f = (p⊕q)r + pq
Method 2
부울 함수가 주어지면 f = p'qr + pq'r + pqr '+ pqr입니다.
Step 1 − 사용 Boolean postulate, x + x = x. 즉, 부울 변수 'n'번을 사용한 논리적 OR 연산은 동일한 변수와 동일합니다. 따라서 마지막 용어 pqr을 두 번 더 쓸 수 있습니다.
⇒ f = p'qr + pq'r + pqr '+ pqr + pqr + pqr
Step 2 − 사용 Distributive law1 일 , 4 일 개 측면, 2 차 및 5 번째 측면, 3 번째 및 여섯 개 번째 관점.
⇒ f = qr (p '+ p) + pr (q'+ q) + pq (r '+ r)
Step 3 − 사용 Boolean postulate, x + x '= 1은 각 괄호 안에있는 항을 단순화합니다.
⇒ f = qr (1) + pr (1) + pq (1)
Step 4 − 사용 Boolean postulate, x.1 = x는 위의 세 항을 단순화합니다.
⇒ f = qr + pr + pq
⇒ f = pq + qr + pr
따라서 단순화 된 부울 함수는 다음과 같습니다. f = pq + qr + pr.
따라서 각 메서드에서 주어진 부울 함수를 단순화 한 후 두 개의 다른 부울 함수를 얻었습니다. 기능적으로이 두 부울 함수는 동일합니다. 따라서 요구 사항에 따라 두 가지 부울 함수 중 하나를 선택할 수 있습니다.
예 2
우리가 complement 부울 함수 f = p'q + pq '.
부울 함수의 보수는 f '= (p'q + pq') '입니다.
Step 1 − DeMorgan의 정리, (x + y) '= x'.y'를 사용합니다.
⇒ f '= (p'q)'. (pq ')'
Step 2 − DeMorgan의 정리, (xy) '= x'+ y '사용
⇒ f '= {(p') '+ q'}. {p '+ (q') '}
Step3 − 부울 가정, (x ')'= x를 사용합니다.
⇒ f '= {p + q'}. {p '+ q}
⇒ f '= pp'+ pq + p'q '+ qq'
Step 4 − 부울 가정, xx '= 0을 사용합니다.
⇒ f = 0 + pq + p'q '+ 0
⇒ f = pq + p'q '
따라서 complement 부울 함수의 p'q + pq '는 pq + p’q’.
두 개의 변수 x와 y를 논리적 AND 연산과 결합하여 4 개의 부울 곱 용어를 얻습니다. 이러한 부울 제품 용어는min terms 또는 standard product terms. 최소 항은 x'y ', x'y, xy'및 xy입니다.
마찬가지로 두 개의 변수 x와 y를 논리 OR 연산과 결합하여 4 개의 부울 합계 항을 얻습니다. 이러한 부울 합계 용어는Max terms 또는 standard sum terms. Max 항은 x + y, x + y ', x'+ y 및 x '+ y'입니다.
다음 표는 2 개의 변수에 대한 최소 항과 MAX 항의 표현을 보여줍니다.
| 엑스 | 와이 | 최소 기간 | 최대 용어 |
|---|---|---|---|
| 0 | 0 | m 0 = x'y ' | 남 0 = x + y |
| 0 | 1 | m 1 = x'y | 남 1 = x + y ' |
| 1 | 0 | m 2 = xy ' | 남 2 = x '+ y |
| 1 | 1 | m 3 = xy | 남 3 = x '+ y' |
이진 변수가 '0'이면 최소 항에서는 변수의 보수로, 최대 항에서는 변수 자체로 표시됩니다. 마찬가지로 이진 변수가 '1'이면 Max 항에서는 변수의 보수로, 최소 항에서는 변수 자체로 표시됩니다.
위의 표에서 최소 항과 최대 항이 서로 보완되어 있음을 쉽게 알 수 있습니다. 'n'개의 부울 변수가있는 경우 2n 개의 최소 항과 2n 개의 최대 항이 있습니다.
표준 SoP 및 PoS 양식
진리표는 입력 및 출력의 집합으로 구성됩니다. 'n'개의 입력 변수가 있으면 0과 1 이있는 2n 개의 가능한 조합이 있습니다. 따라서 각 출력 변수의 값은 입력 변수의 조합에 따라 달라집니다. 따라서 각 출력 변수는 일부 입력 변수 조합에 대해 '1'을, 다른 입력 변수 조합에 대해 '0'을 갖습니다.
따라서 각 출력 변수를 다음 두 가지 방법으로 표현할 수 있습니다.
- 표준 SoP 양식
- 정식 PoS 양식
표준 SoP 양식
Canonical SoP 양식은 Canonical Sum of Products 양식을 의미합니다. 이 양식에서 각 제품 용어에는 모든 리터럴이 포함됩니다. 따라서 이러한 제품 용어는 최소 용어 일뿐입니다. 따라서 표준 SoP 양식은sum of min terms 형태.
먼저 출력 변수가 1 인 최소 항을 식별 한 다음 해당 출력 변수에 해당하는 부울 표현식 (함수)을 얻기 위해 해당 최소 항의 논리 OR을 수행합니다. 이 부울 함수는 최소 항의 합계 형식입니다.
둘 이상의 출력 변수가있는 경우 다른 출력 변수에 대해서도 동일한 절차를 따르십시오.
예
다음을 고려하세요 truth table.
| 입력 | 산출 | ||
|---|---|---|---|
| p | q | r | f |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
여기서 출력 (f)은 4 개의 입력 조합에 대해 '1'입니다. 해당 최소 항은 p'qr, pq'r, pqr ', pqr입니다. 이 4 분 항의 논리 OR을 수행하면 출력 (f)의 부울 함수를 얻을 수 있습니다.
따라서 출력의 부울 함수는 f = p'qr + pq'r + pqr '+ pqr입니다. 이것이canonical SoP form출력, f. 다음 두 가지 표기법으로이 함수를 나타낼 수도 있습니다.
$$f = m_{3}+m_{5}+m_{6}+m_{7}$$
$$f = \sum m\left ( 3,5,6,7 \right )$$
한 방정식에서 우리는 함수를 각 최소 항의 합으로 표현했습니다. 다른 방정식에서 우리는 그 최소 항을 합산하기 위해 기호를 사용했습니다.
정식 PoS 양식
정식 PoS 형식은 합계의 정식 곱 형식을 의미합니다. 이 양식에서 각 합계 용어에는 모든 리터럴이 포함됩니다. 따라서이 합계 항은 Max 항일뿐입니다. 따라서 표준 PoS 형식은product of Max terms 형태.
먼저 출력 변수가 0 인 Max 항을 식별 한 다음 해당 출력 변수에 해당하는 부울 표현식 (함수)을 얻기 위해 해당 Max 항의 논리 AND를 수행합니다. 이 부울 함수는 Max 용어의 곱 형태입니다.
둘 이상의 출력 변수가있는 경우 다른 출력 변수에 대해서도 동일한 절차를 따르십시오.
Example
이전 예의 동일한 진리표를 고려하십시오. 여기서 출력 (f)은 4 개의 입력 조합에 대해 '0'입니다. 해당 Max 항은 p + q + r, p + q + r ', p + q'+ r, p '+ q + r입니다. 이 4 개의 Max 항에 대해 논리 AND를 수행하면 출력 (f)의 부울 함수를 얻을 수 있습니다.
따라서 출력의 부울 함수는 f = (p + q + r). (p + q + r '). (p + q'+ r). (p '+ q + r)입니다. 이것이canonical PoS form출력, f. 다음 두 가지 표기법으로이 함수를 나타낼 수도 있습니다.
$$f=M_{0}.M_{1}.M_{2}.M_{4}$$
$$f=\prod M\left ( 0,1,2,4 \right )$$
한 방정식에서 우리는 함수를 각 Max 항의 곱으로 표현했습니다. 다른 방정식에서 우리는 Max 항의 곱셈을 위해 기호를 사용했습니다.
부울 함수 f = (p + q + r). (p + q + r '). (p + q'+ r). (p '+ q + r)은 부울 함수 f = p'qr + pq'r + pqr '+ pqr.
따라서 표준 SoP 및 표준 PoS 양식은 모두 Dual서로에게. 기능적으로이 두 가지 형태는 동일합니다. 요구 사항에 따라이 두 가지 형식 중 하나를 사용할 수 있습니다.
표준 SoP 및 PoS 양식
부울 출력을 나타내는 두 가지 표준 형식에 대해 논의했습니다. 마찬가지로 부울 출력을 나타내는 두 가지 표준 형식이 있습니다. 이것은 표준 형식의 단순화 된 버전입니다.
- 표준 SoP 양식
- 표준 PoS 양식
이후 장에서 논리 게이트에 대해 설명합니다. 메인advantage표준 형식의 경우 논리 게이트에 적용되는 입력 수를 최소화 할 수 있습니다. 때로는 필요한 총 논리 게이트 수가 감소합니다.
표준 SoP 양식
표준 SoP 양식은 Standard Sum of Products형태. 이 양식에서 각 제품 용어는 모든 리터럴을 포함 할 필요는 없습니다. 따라서 제품 용어는 최소 용어 일 수도 있고 아닐 수도 있습니다. 따라서 표준 SoP 양식은 표준 SoP 양식의 단순화 된 양식입니다.
표준 SoP 형태의 출력 변수를 두 단계로 얻을 수 있습니다.
- 출력 변수의 표준 SoP 형식 가져 오기
- 표준 SoP 형식 인 위의 부울 함수를 단순화하십시오.
둘 이상의 출력 변수가있는 경우 다른 출력 변수에 대해서도 동일한 절차를 따르십시오. 때로는 표준 SoP 양식을 단순화하지 못할 수도 있습니다. 이 경우 표준 및 표준 SoP 양식은 모두 동일합니다.
Example
다음 부울 함수를 표준 SoP 형식으로 변환합니다.
f = p'qr + pq'r + pqr '+ pqr
주어진 부울 함수는 표준 SoP 형식입니다. 이제 표준 SoP 형식을 얻기 위해이 부울 함수를 단순화해야합니다.
Step 1 − 사용 Boolean postulate, x + x = x. 즉, 부울 변수 'n'번을 사용한 논리적 OR 연산은 동일한 변수와 동일합니다. 따라서 마지막 용어 pqr을 두 번 더 쓸 수 있습니다.
⇒ f = p'qr + pq'r + pqr '+ pqr + pqr + pqr
Step 2 − 사용 Distributive law1 일 , 4 일 개 측면, 2 차 및 5 번째 측면, 3 번째 및 여섯 개 번째 관점.
⇒ f = qr (p '+ p) + pr (q'+ q) + pq (r '+ r)
Step 3 − 사용 Boolean postulate, x + x '= 1은 각 괄호 안에있는 항을 단순화합니다.
⇒ f = qr (1) + pr (1) + pq (1)
Step 4 − 사용 Boolean postulate, x.1 = x는 위의 세 항을 단순화합니다.
⇒ f = qr + pr + pq
⇒ f = pq + qr + pr
이것은 단순화 된 부울 함수입니다. 따라서standard SoP form 주어진 표준 SoP 양식에 해당하는 것은 f = pq + qr + pr
표준 PoS 양식
표준 PoS 양식은 Standard Product of Sums형태. 이 양식에서 각 합계 용어는 모든 리터럴을 포함 할 필요는 없습니다. 따라서 합계 항은 최대 항일 수도 있고 아닐 수도 있습니다. 따라서 표준 PoS 형식은 표준 PoS 형식의 단순화 된 형식입니다.
표준 PoS 형식의 출력 변수를 두 단계로 얻습니다.
- 출력 변수의 표준 PoS 형식 가져 오기
- 표준 PoS 형식 인 위의 부울 함수를 단순화하십시오.
둘 이상의 출력 변수가있는 경우 다른 출력 변수에 대해서도 동일한 절차를 따르십시오. 때로는 정식 PoS 양식을 단순화하지 못할 수도 있습니다. 이 경우 표준 및 표준 PoS 양식이 모두 동일합니다.
Example
다음 부울 함수를 표준 PoS 형식으로 변환합니다.
f = (p + q + r). (p + q + r '). (p + q'+ r). (p '+ q + r)
주어진 부울 함수는 정식 PoS 형식입니다. 이제 표준 PoS 양식을 얻기 위해이 부울 함수를 단순화해야합니다.
Step 1 − 사용 Boolean postulate, xx = x. 즉, 부울 변수 'n'번을 사용한 논리적 AND 연산은 동일한 변수와 동일합니다. 따라서 첫 번째 항 p + q + r을 두 번 더 쓸 수 있습니다.
⇒ f = (p + q + r). (p + q + r). (p + q + r). (p + q + r '). (p + q'+ r). (p '+ q + r)
Step 2 − 사용 Distributive law,x + (yz) = (x + y). (x + z) : 첫 번째 및 네 번째 괄호, 두 번째 및 다섯 번째 괄호, 세 번째 및 여섯 번째 괄호.
⇒ f = (p + q + rr '). (p + r + qq'). (q + r + pp ')
Step 3 − 사용 Boolean postulate, x.x '= 0 (각 괄호 안에있는 항을 단순화하기 위해).
⇒ f = (p + q + 0). (p + r + 0). (q + r + 0)
Step 4 − 사용 Boolean postulate, x + 0 = x : 각 괄호 안에있는 항을 단순화
⇒ f = (p + q). (p + r). (q + r)
⇒ f = (p + q). (q + r). (p + r)
이것은 단순화 된 부울 함수입니다. 따라서standard PoS form 주어진 표준 PoS 양식에 해당하는 것은 f = (p + q).(q + r).(p + r). 이것이dual 부울 함수 f = pq + qr + pr.
따라서 표준 SoP 및 표준 PoS 양식은 모두 서로 이중입니다.
이전 장에서는 부울 가정과 정리를 사용하여 부울 함수를 단순화했습니다. 시간이 많이 걸리는 과정이며 각 단계 후에 단순화 된 표현을 다시 작성해야합니다.
이 어려움을 극복하기 위해 Karnaugh부울 함수를 쉽게 단순화하는 방법을 도입했습니다. 이 방법을 Karnaugh 맵 방법 또는 K- 맵 방법이라고합니다. 'n'변수에 대해 2n 개의 셀로 구성된 그래픽 방법 입니다. 인접한 셀은 단일 비트 위치에서만 다릅니다.
2 ~ 5 개의 변수에 대한 K- 맵
K-Map 방법은 2 개 변수의 부울 함수를 5 개 변수로 최소화하는 데 가장 적합합니다. 이제 2 ~ 5 개의 변수에 대한 K-Map에 대해 하나씩 논의 해 보겠습니다.
2 가변 K-Map
2 개의 변수 K-map의 셀 수는 변수의 수가 2 개이므로 4 개입니다. 다음 그림은2 variable K-Map.
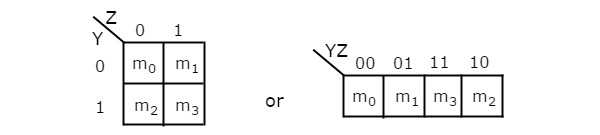
4 개의 인접한 최소 항을 그룹화 할 수있는 가능성은 하나뿐입니다.
2 개의 인접한 min 항을 그룹화 할 수있는 조합은 {(m 0 , m 1 ), (m 2 , m 3 ), (m 0 , m 2 ) 및 (m 1 , m 3 )}입니다.
3 가변 K-Map
변수의 수가 3 개이므로 3 개의 변수 K- 맵의 셀 수는 8 개입니다. 다음 그림은3 variable K-Map.
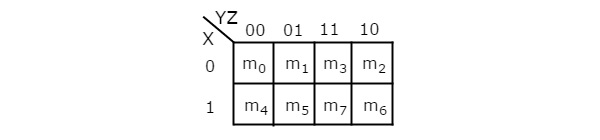
8 개의 인접한 최소 항을 그룹화 할 수있는 가능성은 하나뿐입니다.
4 개의 인접한 min 항을 그룹화 할 수있는 조합은 {(m 0 , m 1 , m 3 , m 2 ), (m 4 , m 5 , m 7 , m 6 ), (m 0 , m 1 , m 4 , m 5 ), (m 1 , m 3 , m 5 , m 7 ), (m 3 , m 2 , m 7 , m 6 ) 및 (m 2 , m 0 , m 6 , m 4 )}.
2 개의 인접한 min 항을 그룹화 할 수있는 조합은 {(m 0 , m 1 ), (m 1 , m 3 ), (m 3 , m 2 ), (m 2 , m 0 ), (m 4 , m 5 )입니다. , (m 5 , m 7 ), (m 7 , m 6 ), (m 6 , m 4 ), (m 0 , m 4 ), (m 1 , m 5 ), (m 3 , m 7 ) 및 ( m 2 , m 6 )}.
x = 0이면 3 개의 변수 K- 맵이 2 개의 변수 K- 맵이됩니다.
4 가변 K-Map
변수의 수가 4 개이므로 4 개의 변수 K- 맵의 셀 수는 16 개입니다. 다음 그림은4 variable K-Map.
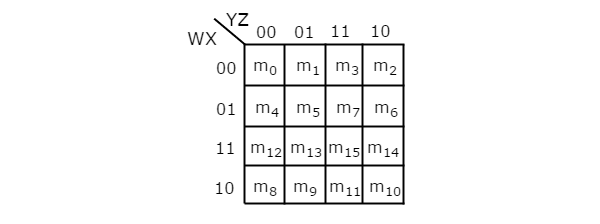
16 개의 인접한 최소 항을 그룹화 할 수있는 가능성은 하나뿐입니다.
R 1 , R 2 , R 3 및 R 4 는 각각 첫 번째 행, 두 번째 행, 세 번째 행 및 네 번째 행의 최소 항을 나타냅니다. 마찬가지로 C 1 , C 2 , C 3 및 C 4 는 각각 첫 번째 열, 두 번째 열, 세 번째 열 및 네 번째 열의 최소 항을 나타냅니다. 8 개의 인접한 min 항을 그룹화 할 수있는 조합은 {(R 1 , R 2 ), (R 2 , R 3 ), (R 3 , R 4 ), (R 4 , R 1 ), (C 1 , C 2 )입니다. , (C 2 , C 3 ), (C 3 , C 4 ), (C 4 , C 1 )}.
w = 0이면 4 개의 변수 K- 맵이 3 개의 변수 K- 맵이됩니다.
5 가변 K-Map
5 개 변수 K-map의 셀 수는 변수 수가 5 개이므로 32 개입니다. 다음 그림은 5 variable K-Map.

32 개의 인접한 최소 항을 그룹화 할 수있는 가능성은 하나뿐입니다.
16 개의 인접한 최소 항을 그룹화하는 두 가지 가능성이 있습니다. 즉, m 0 에서 m 15 및 m 16 에서 m 31 까지의 최소 항 그룹화 .
v = 0이면 5 개의 변수 K- 맵이 4 개의 변수 K- 맵이됩니다.
위의 모든 K- 맵에서 최소 용어 표기법 만 사용했습니다. 마찬가지로 Max 용어 표기법 만 사용할 수 있습니다.
K-Maps를 사용한 부울 함수 최소화
Boolean 함수가 '1'인 입력 조합을 고려하면 Boolean 함수를 얻을 수 있습니다. standard sum of products K-map을 단순화 한 후 양식.
마찬가지로, Boolean 함수가 '0'인 입력 조합을 고려하면 Boolean 함수를 얻을 수 있습니다. standard product of sums K-map을 단순화 한 후 양식.
다음을 따르십시오 rules for simplifying K-maps 제품의 표준 합계 양식을 얻으려면.
부울 함수에있는 변수 수를 기반으로 각 K 맵을 선택합니다.
부울 함수가 최소 항의 합으로 주어지면 K- 맵의 각 최소 항 셀에 배치합니다. 부울 함수가 제품의 합계 형식으로 제공되는 경우 주어진 제품 용어가 유효한 K- 맵의 가능한 모든 셀에 해당 항목을 배치합니다.
인접한 최대 수를 그룹화 할 수 있는지 확인하십시오. 2의 거듭 제곱이어야합니다. 가장 높은 2의 거듭 제곱과 최소 2의 제곱에서 시작합니다. 최고 검정력은 K- 맵에서 고려되는 변수의 수와 같고 최소 검정력은 0입니다.
각 그룹은 리터럴 또는 하나의 제품 용어를 제공합니다. 그것은prime implicant. 주요 함의는 다음과 같다.essential prime implicant, '1'하나 이상이 다른 그룹에 포함되지 않고 해당 그룹 만 포함되는 경우.
모든 주요 함축 및 필수 주요 함축을 기록하십시오. 단순화 된 부울 함수에는 모든 필수 프라임 임 플리 던트와 필수 프라임 임 플리 컨트 만 포함됩니다.
Note 1 − 일부 입력 조합에 대해 출력이 정의되지 않은 경우 해당 출력 값은 다음과 같이 표시됩니다. don’t care symbol ‘x’. 즉, '0'또는 '1'로 간주 할 수 있습니다.
Note 2− do n't care 용어도있는 경우 K-map의 각 셀에 do n't care 'x'를 배치합니다. 인접 항목의 최대 수를 그룹화하는 데 도움이되는 상관 안함 'x'만 고려하십시오. 이러한 경우에는 상관 없음 값을 '1'로 취급하십시오.
예
하자 simplify 다음 부울 함수, f(W, X, Y, Z)= WX’Y’ + WY + W’YZ’ K-map 사용.
주어진 부울 함수는 제품 형태의 합계입니다. 4 개의 변수 W, X, Y & Z가 있습니다. 따라서4 variable K-map. 그만큼4 variable K-map 주어진 제품 용어에 해당하는 항목이 다음 그림에 나와 있습니다.
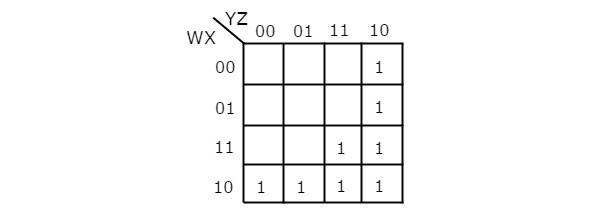
여기서 1은 K-map의 다음 셀에 배치됩니다.
행 4와 열 1 및 2의 교차점에 공통되는 셀은 제품 용어에 해당합니다. WX’Y’.
행 3 및 4와 열 3 및 4의 교차점에 공통되는 셀은 제품 용어에 해당합니다. WY.
행 1과 2와 열 4의 교차점에 공통되는 셀은 제품 용어에 해당합니다. W’YZ’.
인접한 16 개 또는 인접한 8 개를 그룹화 할 수 없습니다. 4 개의 인접한 항목을 그룹화 할 수있는 세 가지 가능성이 있습니다. 이 세 그룹화 후에는 그룹화되지 않은 상태로 남아있는 단일 그룹이 없습니다. 따라서 인접한 2 개의 그룹화를 확인할 필요가 없습니다. 그만큼4 variable K-map 이 세 가지 groupings 다음 그림에 나와 있습니다.

여기에 WX ', WY & YZ'의 세 가지 주요 함의가 있습니다. 이 모든 주요 함의는essential 다음과 같은 이유 때문입니다.
두 사람 (m8 & m9)네 번째 행 그룹은 다른 그룹에 포함되지 않습니다. 네 번째 행 그룹 만이 두 항목을 다룹니다.
하나 하나 (m15)정사각형 모양의 그룹은 다른 그룹에 포함되지 않습니다. 사각형 모양 그룹 만 해당 항목을 다룹니다.
두 사람 (m2 & m6)네 번째 열 그룹의 일부는 다른 그룹에 포함되지 않습니다. 네 번째 열 그룹 만이 두 항목을 다룹니다.
따라서 simplified Boolean function 이다
f = WX’ + WY + YZ’
다음을 따르십시오 rules for simplifying K-maps 합계 형식의 표준 제품을 얻으려면.
부울 함수에있는 변수 수를 기반으로 각 K 맵을 선택합니다.
Boolean 함수가 Max 항의 곱으로 주어지면 K- 맵의 각 Max 항 셀에 0을 배치합니다. 부울 함수가 합계 형식의 곱으로 제공되는 경우 주어진 합계 항이 유효한 K- 맵의 가능한 모든 셀에 0을 배치합니다.
인접한 0의 최대 수를 그룹화 할 수 있는지 확인하십시오. 2의 거듭 제곱이어야합니다. 가장 높은 2의 거듭 제곱과 최소 2의 제곱에서 시작합니다. 최고 검정력은 K- 맵에서 고려되는 변수의 수와 같고 최소 검정력은 0입니다.
각 그룹은 리터럴 또는 하나의 합계 용어를 제공합니다. 그것은prime implicant. 주요 함의는 다음과 같다.essential prime implicant, '0'하나 이상이 다른 그룹에 포함되지 않고 해당 그룹 만 포함되는 경우.
모든 주요 함축 및 필수 주요 함축을 기록하십시오. 단순화 된 부울 함수에는 모든 필수 프라임 임 플리 던트와 필수 프라임 임 플리 컨트 만 포함됩니다.
Note− do n't care 용어도있는 경우 K-map의 각 셀에 do n't care 'x'를 배치합니다. 인접한 0의 최대 수를 그룹화하는 데 도움이되는 상관 안함 'x'만 고려하십시오. 이러한 경우에는 상관 없음 값을 '0'으로 처리하십시오.
예
하자 simplify 다음 부울 함수, $f\left ( X,Y,Z \right )=\prod M\left ( 0,1,2,4 \right )$ K-map 사용.
주어진 부울 함수는 Max 용어 형식의 곱입니다. 3 개의 변수 X, Y, Z가 있습니다. 따라서 3 개의 변수 K- 맵이 필요합니다. 주어진 Max 항은 M 0 , M 1 , M 2 & M 4 입니다. 3variable K-map 주어진 Max 항에 해당하는 0이 다음 그림에 나와 있습니다.

8 개의 인접한 0 또는 4 개의 인접한 0을 그룹화 할 수 없습니다. 2 개의 인접한 0을 그룹화 할 수있는 세 가지 가능성이 있습니다. 이 세 그룹화 후에는 그룹화되지 않은 단일 0이 남지 않습니다. 그만큼3 variable K-map 이 세 가지 groupings 다음 그림에 나와 있습니다.

여기에 세 가지 주요 함축 물 X + Y, Y + Z & Z + X가 있습니다. essential 각 그룹의 하나의 0은 개별 그룹을 제외하고는 다른 그룹에 포함되지 않기 때문입니다.
따라서 simplified Boolean function 이다
f = (X + Y).(Y + Z).(Z + X)
이렇게하면 K-map 방법을 사용하여 최대 5 개의 변수까지 부울 함수를 쉽게 단순화 할 수 있습니다. 5 개 이상의 변수의 경우 K-Maps를 사용하여 기능을 단순화하기가 어렵습니다. 왜냐하면cells K-map에서 doubled 새 변수를 포함합니다.
이 검사 및 인접 항목 (최소 용어) 또는 인접한 0 (최대 용어)의 그룹화는 복잡합니다. 우리는 논의 할 것이다Tabular method K-map 방식의 어려움을 극복하기 위해 다음 장에서
이전 장에서는 최대 5 개의 변수까지 불리언 함수를 최소화하는 편리한 방법 인 K-map 방법에 대해 설명했습니다. 그러나이 방법을 사용하면 변수가 5 개 이상인 Boolean 함수를 단순화하기가 어렵습니다.
Quine-McClukey 표 형식 방법은 주요 함축 개념을 기반으로 한 표 형식 방법입니다. 우리는 알고 있습니다prime implicant 주어진 부울 함수의 다른 제품 (또는 합계) 용어와 결합하여 더 이상 줄일 수없는 제품 (또는 합계) 용어입니다.
이 테이블 형식 방법은 다음 부울 ID를 반복적으로 사용하여 주요 함축을 가져 오는 데 유용합니다.
xy + xy '= x (y + y') = x.1 = x
Quine-McCluskey 표 형식 방법의 절차
Quine-McClukey 표 형식 방법을 사용하여 부울 함수를 단순화하려면 다음 단계를 따르십시오.
Step 1 − 주어진 최소 항을 ascending order이진 표현에있는 1의 수를 기반으로 그룹을 만듭니다. 그래서at most ‘n+1’ groups 부울 함수에 'n'부울 변수가 있거나 최소 항에 해당하는 이진에 'n'비트가있는 경우.
Step 2 −에 존재하는 최소 용어 비교 successive groups. 1 비트 위치에만 변경이있는 경우이 두 개의 최소 항 쌍을 취하십시오. 이 기호 '_'를 다른 비트 위치에 놓고 나머지 비트를 그대로 유지합니다.
Step 3 − 모든 것을 얻을 때까지 새로 형성된 용어로 2 단계를 반복합니다. prime implicants.
Step 4 − 공식화 prime implicant table. 행과 열의 집합으로 구성됩니다. 프라임 임 플리 던 트는 행 단위로 배치 할 수 있고 최소 용어는 열 단위로 배치 할 수 있습니다. 각 프라임 임 플리 던트에서 다루는 최소 항에 해당하는 셀에 '1'을 넣으십시오.
Step 5− 각 열을 관찰하여 필수 주요 함의를 찾습니다. 최소 기간이 하나의 주요 함 축사에 의해서만 포함되는 경우essential prime implicant. 이러한 필수 주요 의미는 단순화 된 부울 함수의 일부입니다.
Step 6− 각 필수 프라임 임 플리 던트의 행과 해당 필수 프라임 임 플리 던트에서 다루는 최소 용어에 해당하는 열을 제거하여 프라임 임 플리 던트 테이블을 줄이십시오. 감소 된 프라임 암시 테이블에 대해 5 단계를 반복합니다. 주어진 부울 함수의 모든 최소 항이 끝나면이 프로세스를 중지하십시오.
예
하자 simplify 다음 부울 함수, $f\left ( W,X,Y,Z \right )=\sum m\left ( 2,6,8,9,10,11,14,15 \right )$ Quine-McClukey 표 방식을 사용합니다.
주어진 부울 함수는 sum of min terms형태. 4 개의 변수 W, X, Y & Z가 있습니다. 주어진 최소 항은 2, 6, 8, 9, 10, 11, 14 및 15입니다.이 최소 항의 오름차순은 해당 항목에있는 항목의 수를 기준으로합니다. 이진수는 2, 8, 6, 9, 10, 11, 14 및 15입니다. 다음 표는 이러한min terms and their equivalent binary 표현.
| 그룹 이름 | 최소 기간 | W | 엑스 | 와이 | 지 |
|---|---|---|---|---|---|
| GA1 | 2 | 0 | 0 | 1 | 0 |
| 8 | 1 | 0 | 0 | 0 | |
| GA2 | 6 | 0 | 1 | 1 | 0 |
| 9 | 1 | 0 | 0 | 1 | |
| 10 | 1 | 0 | 1 | 0 | |
| 11 | 1 | 0 | 1 | 1 | |
| 14 | 1 | 1 | 1 | 0 | |
| GA4 | 15 | 1 | 1 | 1 | 1 |
주어진 최소 항은 이진 등가물에있는 항목의 수를 기준으로 4 개의 그룹으로 정렬됩니다. 다음 표는 가능한merging of min terms 인접한 그룹에서.
| 그룹 이름 | 최소 기간 | W | 엑스 | 와이 | 지 |
|---|---|---|---|---|---|
| GB1 | 2,6 | 0 | - | 1 | 0 |
| 2,10 | - | 0 | 1 | 0 | |
| 8,9 | 1 | 0 | 0 | - | |
| 8,10 | 1 | 0 | - | 0 | |
| GB2 | 6,14 | - | 1 | 1 | 0 |
| 9,11 | 1 | 0 | - | 1 | |
| 10,11 | 1 | 0 | 1 | - | |
| 10,14 | 1 | - | 1 | 0 | |
| 11,15 | 1 | - | 1 | 1 | |
| 14,15 | 1 | 1 | 1 | - |
인접 그룹과 1 비트 위치에서만 다른 최소 용어가 병합됩니다. 다른 비트는이 기호 '-'로 표시됩니다. 이 경우 세 개의 그룹이 있고 각 그룹에는 2 개의 최소 용어 조합이 포함됩니다. 다음 표는 가능한merging of min term pairs 인접한 그룹에서.
| 그룹 이름 | 최소 기간 | W | 엑스 | 와이 | 지 |
|---|---|---|---|---|---|
| GB1 | 2,6,10,14 | - | - | 1 | 0 |
| 2,10,6,14 | - | - | 1 | 0 | |
| 8,9,10,11 | 1 | 0 | - | - | |
| 8,10,9,11 | 1 | 0 | - | - | |
| GB2 | 10,11,14,15 | 1 | - | 1 | - |
| 10,14,11,15 | 1 | - | 1 | - |
1 비트 위치에서만 다른 연속적인 최소 항 쌍 그룹이 병합됩니다. 다른 비트는이 기호 '-'로 표시됩니다. 이 경우 두 개의 그룹이 있으며 각 그룹에는 4 개의 최소 용어 조합이 포함됩니다. 여기에서 이러한 4 분 용어 조합은 두 행으로 제공됩니다. 따라서 반복되는 행을 제거 할 수 있습니다. 중복 행을 제거한 후 축소 된 테이블은 다음과 같습니다.
| 그룹 이름 | 최소 기간 | W | 엑스 | 와이 | 지 |
|---|---|---|---|---|---|
| GC1 | 2,6,10,14 | - | - | 1 | 0 |
| 8,9,10,11 | 1 | 0 | - | - | |
| GC2 | 10,11,14,15 | 1 | - | 1 | - |
인접 그룹의 최소 용어 조합은 1 비트 이상의 위치에서 다르기 때문에 더 이상 병합 할 수 없습니다. 위 표에는 3 개의 행이 있습니다. 따라서 각 행은 하나의 주요 함축을 제공합니다. 따라서prime implicants YZ ', WX'및 WY입니다.
그만큼 prime implicant table 아래에 나와 있습니다.
| 최소 용어 / 프라임 임 플리 던트 | 2 | 6 | 8 | 9 | 10 | 11 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|
| YZ’ | 1 | 1 | 1 | 1 | ||||
| WX’ | 1 | 1 | 1 | 1 | ||||
| WY | 1 | 1 | 1 | 1 |
주요 의미는 행 단위로 배치되고 최소 용어는 열 단위로 배치됩니다. 1은 주요 함축 행과 해당 최소 항 열의 공통 셀에 배치됩니다.
최소 용어 2와 6은 단 하나의 주요 함 축사에 의해 다루어집니다. YZ’. 그래서, 그것은essential prime implicant. 이것은 단순화 된 부울 함수의 일부가됩니다. 이제이 주요 함축 행과 해당 최소 항 열을 제거합니다. 축소 된 프라임 관련 테이블이 아래에 나와 있습니다.
| 최소 용어 / 프라임 임 플리 던트 | 8 | 9 | 11 | 15 |
|---|---|---|---|---|
| WX’ | 1 | 1 | 1 | |
| WY | 1 | 1 |
최소 용어 8과 9는 단 하나의 주요 함 축사에 의해서만 다루어집니다. WX’. 그래서, 그것은essential prime implicant. 이것은 단순화 된 부울 함수의 일부가됩니다. 이제이 주요 함축 행과 해당 최소 항 열을 제거합니다. 축소 된 프라임 관련 테이블이 아래에 나와 있습니다.
| 최소 용어 / 프라임 임 플리 던트 | 15 |
|---|---|
| WY | 1 |
최소 기간 15는 단 하나의 주요 암시 자에 의해 다루어집니다. WY. 그래서, 그것은essential prime implicant. 이것은 단순화 된 부울 함수의 일부가됩니다.
이 예제 문제에서 우리는 세 가지 주요 함의를 얻었고 세 가지 모두 필수입니다. 따라서simplified Boolean function 이다
f(W,X,Y,Z) = YZ’ + WX’ + WY.
디지털 전자 회로는 다음 전압으로 작동합니다. two logic levels즉 Logic Low 및 Logic High입니다. Logic Low에 해당하는 전압 범위는 '0'으로 표시됩니다. 마찬가지로 Logic High에 해당하는 전압 범위는 '1'로 표시됩니다.
하나 이상의 입력과 단일 출력이있는 기본 디지털 전자 회로는 Logic gate. 따라서 논리 게이트는 모든 디지털 시스템의 빌딩 블록입니다. 이러한 논리 게이트를 다음 세 가지 범주로 분류 할 수 있습니다.
- 기본 게이트
- 유니버설 게이트
- 특수 게이트
이제 각 카테고리 아래에 하나씩 논리 게이트에 대해 논의하겠습니다.
기본 게이트
이전 장에서 부울 함수는 요구 사항에 따라 제품 합계 형식 또는 합계 형식으로 표현할 수 있음을 배웠습니다. 따라서 기본 게이트를 사용하여 이러한 부울 함수를 구현할 수 있습니다. 기본 게이트는 AND, OR 및 NOT 게이트입니다.
AND 게이트
AND 게이트는 두 개 이상의 입력이 있고 출력을 생성하는 디지털 회로입니다. logical AND모든 입력의. 표시하는 것은 선택 사항입니다.Logical AND 기호 '.'와 함께.
다음 표는 truth table 2 입력 AND 게이트의.
| ㅏ | 비 | Y = AB |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
여기서 A, B는 입력이고 Y는 두 입력 AND 게이트의 출력입니다. 두 입력이 모두 '1'이면 출력 만 Y는 '1'입니다. 나머지 입력 조합의 경우 출력 Y는 '0'입니다.
다음 그림은 symbol 두 개의 입력 A, B와 하나의 출력 Y를 갖는 AND 게이트의.

이 AND 게이트는 출력 (Y)을 생성합니다. logical AND마찬가지로, 'n'개의 입력이 있으면 AND 게이트는 모든 입력의 논리적 AND 인 출력을 생성합니다. 즉, 모든 입력이 '1'일 때 AND 게이트의 출력은 '1'이됩니다.
OR 게이트
OR 게이트는 두 개 이상의 입력이 있고 모든 입력의 논리적 OR 인 출력을 생성하는 디지털 회로입니다. 이logical OR 기호 '+'로 표시됩니다.
다음 표는 truth table 2 입력 OR 게이트의.
| ㅏ | 비 | Y = A + B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Here A, B are the inputs and Y is the output of two input OR gate. If both inputs are ‘0’, then only the output, Y is ‘0’. For remaining combinations of inputs, the output, Y is ‘1’.
The following figure shows the symbol of an OR gate, which is having two inputs A, B and one output, Y.

This OR gate produces an output (Y), which is the logical OR of two inputs A, B. Similarly, if there are ‘n’ inputs, then the OR gate produces an output, which is the logical OR of all those inputs. That means, the output of an OR gate will be ‘1’, when at least one of those inputs is ‘1’.
NOT gate
A NOT gate is a digital circuit that has single input and single output. The output of NOT gate is the logical inversion of input. Hence, the NOT gate is also called as inverter.
The following table shows the truth table of NOT gate.
| A | Y = A’ |
|---|---|
| 0 | 1 |
| 1 | 0 |
Here A and Y are the input and output of NOT gate respectively. If the input, A is ‘0’, then the output, Y is ‘1’. Similarly, if the input, A is ‘1’, then the output, Y is ‘0’.
The following figure shows the symbol of NOT gate, which is having one input, A and one output, Y.

This NOT gate produces an output (Y), which is the complement of input, A.
Universal gates
NAND & NOR gates are called as universal gates. Because we can implement any Boolean function, which is in sum of products form by using NAND gates alone. Similarly, we can implement any Boolean function, which is in product of sums form by using NOR gates alone.
NAND gate
NAND gate is a digital circuit that has two or more inputs and produces an output, which is the inversion of logical AND of all those inputs.
The following table shows the truth table of 2-input NAND gate.
| A | B | Y = (A.B)’ |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Here A, B are the inputs and Y is the output of two input NAND gate. When both inputs are ‘1’, the output, Y is ‘0’. If at least one of the input is zero, then the output, Y is ‘1’. This is just opposite to that of two input AND gate operation.
The following image shows the symbol of NAND gate, which is having two inputs A, B and one output, Y.
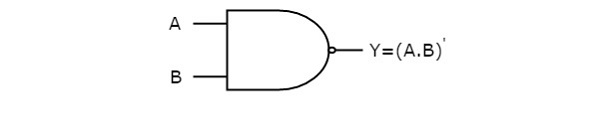
NAND gate operation is same as that of AND gate followed by an inverter. That’s why the NAND gate symbol is represented like that.
NOR gate
NOR gate is a digital circuit that has two or more inputs and produces an output, which is the inversion of logical OR of all those inputs.
The following table shows the truth table of 2-input NOR gate
| A | B | Y = (A+B)’ |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Here A, B are the inputs and Y is the output. If both inputs are ‘0’, then the output, Y is ‘1’. If at least one of the input is ‘1’, then the output, Y is ‘0’. This is just opposite to that of two input OR gate operation.
The following figure shows the symbol of NOR gate, which is having two inputs A, B and one output, Y.

NOR gate operation is same as that of OR gate followed by an inverter. That’s why the NOR gate symbol is represented like that.
Special Gates
Ex-OR & Ex-NOR gates are called as special gates. Because, these two gates are special cases of OR & NOR gates.
Ex-OR gate
The full form of Ex-OR gate is Exclusive-OR gate. Its function is same as that of OR gate except for some cases, when the inputs having even number of ones.
The following table shows the truth table of 2-input Ex-OR gate.
| A | B | Y = A⊕B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Here A, B are the inputs and Y is the output of two input Ex-OR gate. The truth table of Ex-OR gate is same as that of OR gate for first three rows. The only modification is in the fourth row. That means, the output (Y) is zero instead of one, when both the inputs are one, since the inputs having even number of ones.
Therefore, the output of Ex-OR gate is ‘1’, when only one of the two inputs is ‘1’. And it is zero, when both inputs are same.
Below figure shows the symbol of Ex-OR gate, which is having two inputs A, B and one output, Y.

Ex-OR gate operation is similar to that of OR gate, except for few combination(s) of inputs. That’s why the Ex-OR gate symbol is represented like that. The output of Ex-OR gate is ‘1’, when odd number of ones present at the inputs. Hence, the output of Ex-OR gate is also called as an odd function.
Ex-NOR gate
The full form of Ex-NOR gate is Exclusive-NOR gate. Its function is same as that of NOR gate except for some cases, when the inputs having even number of ones.
The following table shows the truth table of 2-input Ex-NOR gate.
| A | B | Y = A⊙B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Here A, B are the inputs and Y is the output. The truth table of Ex-NOR gate is same as that of NOR gate for first three rows. The only modification is in the fourth row. That means, the output is one instead of zero, when both the inputs are one.
Therefore, the output of Ex-NOR gate is ‘1’, when both inputs are same. And it is zero, when both the inputs are different.
The following figure shows the symbol of Ex-NOR gate, which is having two inputs A, B and one output, Y.

Ex-NOR gate operation is similar to that of NOR gate, except for few combination(s) of inputs. That’s why the Ex-NOR gate symbol is represented like that. The output of Ex-NOR gate is ‘1’, when even number of ones present at the inputs. Hence, the output of Ex-NOR gate is also called as an even function.
From the above truth tables of Ex-OR & Ex-NOR logic gates, we can easily notice that the Ex-NOR operation is just the logical inversion of Ex-OR operation.
The maximum number of levels that are present between inputs and output is two in two level logic. That means, irrespective of total number of logic gates, the maximum number of Logic gates that are present (cascaded) between any input and output is two in two level logic. Here, the outputs of first level Logic gates are connected as inputs of second level Logic gate(s).
Consider the four Logic gates AND, OR, NAND & NOR. Since, there are 4 Logic gates, we will get 16 possible ways of realizing two level logic. Those are AND-AND, AND-OR, ANDNAND, AND-NOR, OR-AND, OR-OR, OR-NAND, OR-NOR, NAND-AND, NAND-OR, NANDNAND, NAND-NOR, NOR-AND, NOR-OR, NOR-NAND, NOR-NOR.
These two level logic realizations can be classified into the following two categories.
- Degenerative form
- Non-degenerative form
Degenerative Form
If the output of two level logic realization can be obtained by using single Logic gate, then it is called as degenerative form. Obviously, the number of inputs of single Logic gate increases. Due to this, the fan-in of Logic gate increases. This is an advantage of degenerative form.
Only 6 combinations of two level logic realizations out of 16 combinations come under degenerative form. Those are AND-AND, AND-NAND, OR-OR, OR-NOR, NAND-NOR, NORNAND.
In this section, let us discuss some realizations. Assume, A, B, C & D are the inputs and Y is the output in each logic realization.
AND-AND Logic
In this logic realization, AND gates are present in both levels. Below figure shows an example for AND-AND logic realization.

We will get the outputs of first level logic gates as $Y_{1}=AB$ and $Y_{2}=CD$
These outputs, $Y_{1}$ and $Y_{2}$ are applied as inputs of AND gate that is present in second level. So, the output of this AND gate is
$$Y=Y_{1}Y_{2}$$
Substitute $Y_{1}$ and $Y_{2}$ values in the above equation.
$$Y=\left ( AB \right )\left ( CD \right )$$
$\Rightarrow Y=ABCD$
Therefore, the output of this AND-AND logic realization is ABCD. This Boolean function can be implemented by using a 4 input AND gate. Hence, it is degenerative form.
AND-NAND Logic
In this logic realization, AND gates are present in first level and NAND gate(s) are present in second level. The following figure shows an example for AND-NAND logic realization.
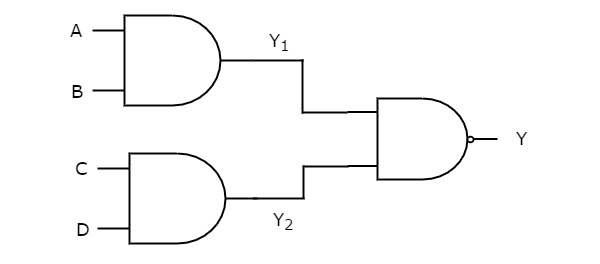
이전에는 첫 번째 레벨 로직 게이트의 출력을 다음과 같이 얻었습니다. $Y_{1} = AB$ 과 $Y_{2} = CD$
이러한 출력은$Y_{1}$ 과 $Y_{2}$두 번째 레벨에 존재하는 NAND 게이트의 입력으로 적용됩니다. 따라서이 NAND 게이트의 출력은
$$Y={\left ( Y_{1}Y_{2} \right )}'$$
대용품 $Y_{1}$ 과 $Y_{2}$ 위 방정식의 값.
$$Y={\left ( \left ( AB \right ) \left ( CD \right )\right )}'$$
$\Rightarrow Y={\left ( ABCD \right )}'$
따라서이 AND-NAND 논리 실현의 출력은 다음과 같습니다. ${\left ( ABCD \right )}'$. 이 부울 함수는 4 입력 NAND 게이트를 사용하여 구현할 수 있습니다. 따라서degenerative form.
OR-OR 논리
이 논리 실현에서 OR 게이트는 두 레벨 모두에 존재합니다. 다음 그림은OR-OR logic 실현.
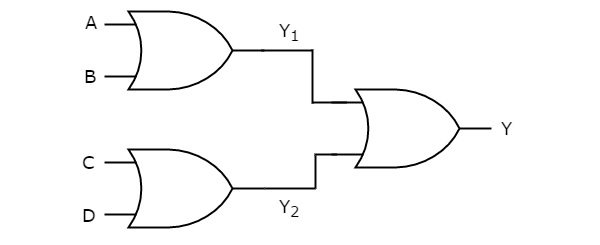
첫 번째 레벨 논리 게이트의 출력을 다음과 같이 얻을 수 있습니다. $Y_{1}=A+B$ 과 $Y_{2}=C+D$.
이러한 출력은 $Y_{1}$ 과 $Y_{2}$두 번째 레벨에 존재하는 OR 게이트의 입력으로 적용됩니다. 따라서이 OR 게이트의 출력은
$$Y=Y_{1}+Y_{2}$$
대용품 $Y_{1}$ 과 $Y_{2}$ 위 방정식의 값.
$$Y=\left ( A+B \right )+\left ( C+D \right )$$
$\Rightarrow Y=A+B+C+D$
따라서이 OR-OR 논리 실현의 출력은 다음과 같습니다. A+B+C+D. 이 부울 함수는 4 개의 입력 OR 게이트를 사용하여 구현할 수 있습니다. 따라서degenerative form.
마찬가지로 나머지 실현이이 범주에 속하는지 여부를 확인할 수 있습니다.
비 퇴행성 형태
단일 논리 게이트를 사용하여 2 단계 논리 실현의 출력을 얻을 수없는 경우 다음과 같이 호출됩니다. non-degenerative form.
나머지 10 combinations두 가지 수준의 논리 실현은 비 퇴행 적 형태로 나타납니다. AND-OR, AND-NOR, OR-AND, OR-NAND, NAND-AND, NANDOR, NAND-NAND, NOR-AND, NOR-OR, NOR-NOR입니다.
이제 몇 가지 실현에 대해 논의하겠습니다. A, B, C & D가 입력이고 Y가 각 논리 실현의 출력이라고 가정합니다.
AND-OR 논리
이 논리 실현에서 AND 게이트는 첫 번째 레벨에 존재하고 OR 게이트 (들)는 두 번째 레벨에 존재합니다. 아래 그림은AND-OR logic 실현.

이전에는 첫 번째 레벨 로직 게이트의 출력을 다음과 같이 얻었습니다. $Y_{1} = AB$ 과 $Y_{2} = CD$.
이러한 출력 Y1 및 Y2는 두 번째 레벨에 존재하는 OR 게이트의 입력으로 적용됩니다. 따라서이 OR 게이트의 출력은
$$Y=Y_{1}+Y_{2}$$
대용품 $Y_{1}$ 과 $Y_{2}$ 위 방정식의 값
$$Y=AB+CD$$
따라서이 AND-OR 논리 실현의 출력은 다음과 같습니다. AB+CD. 이 부울 함수는Sum of Products형태. 단일 논리 게이트를 사용하여 구현할 수 없기 때문에이 AND-OR 논리 구현은non-degenerative form.
AND-NOR 논리
이 논리 실현에서 AND 게이트는 첫 번째 레벨에 존재하고 NOR 게이트 (들)는 두 번째 레벨에 존재합니다. 다음 그림은AND-NOR logic 실현.

우리는 첫 번째 레벨 로직 게이트의 출력을 다음과 같이 알고 있습니다. $Y_{1} = AB$ 과 $Y_{2} = CD$
이러한 출력 Y1 및 Y2는 두 번째 레벨에있는 NOR 게이트의 입력으로 적용됩니다. 따라서이 NOR 게이트의 출력은
$$Y={\left ( Y_{1}+Y_{2} \right )}'$$
대용품 $Y_{1}$ 과 $Y_{2}$ 위 방정식의 값.
$$Y={\left ( AB+CD \right )}'$$
따라서이 AND-NOR 논리 실현의 출력은 다음과 같습니다. ${\left ( AB+CD \right )}'$. 이 부울 함수는AND-OR-Invert형태. 단일 논리 게이트를 사용하여 구현할 수 없기 때문에이 AND-NOR 논리 구현은non-degenerative form
OR-AND 논리
이 논리 실현에서 OR 게이트는 첫 번째 레벨에 존재하고 AND 게이트 (들)는 두 번째 레벨에 존재합니다. 다음 그림은OR-AND logic 실현.

이전에는 첫 번째 레벨 로직 게이트의 출력을 다음과 같이 얻었습니다. $Y_{1}=A+B$ 과 $Y_{2}=C+D$.
이러한 출력은 $Y_{1}$ 과 $Y_{2}$두 번째 레벨에 존재하는 AND 게이트의 입력으로 적용됩니다. 따라서이 AND 게이트의 출력은
$$Y=Y_{1}Y_{2}$$
대용품 $Y_{1}$ 과 $Y_{2}$ 위 방정식의 값.
$$Y = \left ( A+B \right )\left ( C+D \right )$$
따라서이 OR-AND 논리 실현의 출력은 다음과 같습니다. (A + B) (C + D). 이 부울 함수는Product of Sums형태. 단일 논리 게이트를 사용하여 구현할 수 없기 때문에이 OR-AND 논리 구현은non-degenerative form.
마찬가지로 나머지 실현이이 범주에 속하는지 여부를 확인할 수 있습니다.
Combinational circuits논리 게이트로 구성됩니다. 이 회로는 이진 값으로 작동합니다. 조합 회로의 출력은 현재 입력의 조합에 따라 달라집니다. 다음 그림은block diagram 조합 회로의.

이 조합 회로에는 'n'입력 변수와 'm'출력이 있습니다. 입력 변수의 각 조합은 출력에 영향을줍니다.
조합 회로의 설계 절차
주어진 사양에서 필요한 수의 입력 변수 및 출력을 찾습니다.
공식화 Truth table. 'n'개의 입력 변수가 있으면 2n 개의 가능한 조합이 있습니다. 각 입력 조합에 대해 출력 값을 찾으십시오.
찾기 Boolean expressions각 출력에 대해. 필요한 경우 이러한 식을 단순화하십시오.
다음을 사용하여 각 출력에 해당하는 위의 부울 표현식을 구현하십시오. Logic gates.
코드 변환기
코드라는 장에서 다양한 코드에 대해 논의했습니다. 한 코드를 다른 코드로 변환하는 변환기는 다음과 같이 호출됩니다.code converters. 이 코드 변환기는 기본적으로 논리 게이트로 구성됩니다.
예
바이너리 코드에서 그레이 코드로의 변환기
4 비트 바이너리 코드 WXYZ를 동등한 그레이 코드 ABCD로 변환하는 변환기를 구현해 보겠습니다.
다음 표는 Truth table 4 비트 바이너리 코드를 그레이 코드로 변환합니다.
| 이진 코드 WXYZ | WXYZ 회색 코드 ABCD |
|---|---|
| 0000 | 0000 |
| 0001 | 0001 |
| 0010 | 0011 |
| 0011 | 0010 |
| 0100 | 0110 |
| 0101 | 0111 |
| 0110 | 0101 |
| 0111 | 0100 |
| 1000 | 1100 년 |
| 1001 | 1101 |
| 1010 년 | 1111 년 |
| 1011 | 1110 년 |
| 1100 년 | 1010 년 |
| 1101 | 1011 |
| 1110 년 | 1001 |
| 1111 년 | 1000 |
진실 테이블에서 우리는 Boolean functions 아래와 같이 그레이 코드의 각 출력 비트에 대해.
$$A=\sum m\left (8,9,10,11,12,13,14,15 \right )$$
$$B=\sum m\left (4,5,6,7,8,9,10,11 \right )$$
$$C=\sum m\left (2,3,4,5,10,11,12,13 \right )$$
$$D=\sum m\left (1,2,5,6,9,10,13,14 \right )$$
4 개의 변수 K-Map을 사용하여 위의 함수를 단순화 해 보겠습니다.
다음 그림은 4 variable K-Map 단순화를 위해 Boolean function, A.

인접한 8 개를 그룹화하여 $A=W$.
다음 그림은 4 variable K-Map 단순화를 위해 Boolean function, B.

인접한 4 개의 그룹으로 구성된 두 그룹이 있습니다. 그룹화 후 B를
$$B={W}'X+W{X}'=W\oplus X $$
마찬가지로 단순화 후 C & D에 대해 다음과 같은 부울 함수를 얻습니다.
$$C={X}'Y+X{Y}'=X \oplus Y$$
$$D={Y}'Z+Y{Z}'=Y \oplus Z$$
다음 그림은 circuit diagram 4 비트 바이너리 코드를 그레이 코드로 변환합니다.

출력은 현재 입력에만 의존하기 때문에이 4 비트 바이너리 코드-그레이 코드 변환기는 조합 회로입니다. 마찬가지로 다른 코드 변환기를 구현할 수 있습니다.
패리티 비트 생성기
생성되는 패리티 비트 유형에 따라 두 가지 유형의 패리티 비트 생성기가 있습니다. Even parity generator짝수 패리티 비트를 생성합니다. 비슷하게,odd parity generator 홀수 패리티 비트를 생성합니다.
심지어 패리티 생성기
이제 3 비트 이진 입력 WXY에 대해 짝수 패리티 생성기를 구현해 보겠습니다. 짝수 패리티 비트 P를 생성합니다. 입력에 홀수의 1이 있으면 짝수 패리티 비트 P는 결과 단어에 짝수 1이 포함되도록 '1'이어야합니다. 다른 입력 조합, 심지어 패리티 비트의 경우 P는 '0'이어야합니다. 다음 표는Truth table 짝수 패리티 생성기.
| 이진 입력 WXY | 짝수 패리티 비트 P |
|---|---|
| 000 | 0 |
| 001 | 1 |
| 010 | 1 |
| 011 | 0 |
| 100 | 1 |
| 101 | 0 |
| 110 | 0 |
| 111 | 1 |
위의 진리표에서 우리는 Boolean function 패리티 비트를 위해
$$P={W}'{X}'Y+{W}'X{Y}'+W{X}'{Y}'+WXY$$
$\Rightarrow P={W}'\left ( {X}'Y+X{Y}' \right )+W\left ({X}'{Y}'+XY \right )$
$\Rightarrow P={W}'\left ( X \oplus Y \right )+W{\left (X \oplus Y \right )}'=W \oplus X \oplus Y$
다음 그림은 circuit diagram 짝수 패리티 생성기.

이 회로는 두 개의 Exclusive-OR gates각각 두 개의 입력이 있습니다. 두 개의 입력 W & X를 갖는 첫 번째 ExclusiveOR 게이트는 출력 W ⊕ X를 생성합니다.이 출력은 두 번째 Exclusive-OR 게이트의 한 입력으로 제공됩니다. 이 두 번째 Exclusive-OR 게이트의 다른 입력은 Y이고 W ⊕ X ⊕ Y의 출력을 생성합니다.
홀수 패리티 생성기
입력에 1이 짝수이면 홀수 패리티 비트, P는 '1'이되어야 결과 단어에 홀수 1이 포함됩니다. 다른 입력 조합, 홀수 패리티 비트의 경우 P는 '0'이어야합니다.
홀수 패리티 생성기를 구현하려면 짝수 패리티 생성기와 동일한 절차를 따르십시오. 그만큼circuit diagram 홀수 패리티 생성기의 구성은 다음 그림과 같습니다.

위의 회로도는 첫 번째 레벨의 Ex-OR 게이트와 두 번째 레벨의 Ex-NOR 게이트로 구성됩니다. 홀수 패리티는 짝수 패리티와 정반대이므로 짝수 패리티 생성기의 출력에 인버터를 배치 할 수 있습니다. 이 경우 첫 번째 및 두 번째 레벨은 각 레벨에 ExOR 게이트를 포함하고 세 번째 레벨은 인버터로 구성됩니다.
패리티 검사기
검사해야 할 패리티 유형에 따라 두 가지 유형의 패리티 검사기가 있습니다. Even parity checker짝수 패리티와 함께 메시지 비트를 포함하는 전송 된 데이터의 오류를 확인합니다. 비슷하게,odd parity checker 홀수 패리티와 함께 메시지 비트를 포함하는 전송 된 데이터의 오류를 확인합니다.
심지어 패리티 검사기
이제 짝수 패리티 검사기 회로를 구현해 보겠습니다. 3 비트 이진 입력을 가정하면 WXY는 짝수 패리티 비트 P와 함께 전송됩니다. 따라서 결과 단어 (데이터)에는 4 비트가 포함되며 이는 짝수 패리티 검사기의 입력으로 수신됩니다.
그것은 생성 even parity check bit, E. 수신 된 데이터에 1이 짝수 인 경우이 비트는 0이됩니다. 이는 수신 된 데이터에 오류가 없음을 의미합니다. 이 짝수 패리티 검사 비트는 수신 된 데이터에 홀수 개의 1이 포함되어있는 경우 1이됩니다. 이는 수신 된 데이터에 오류가 있음을 의미합니다.
다음 표는 Truth table 짝수 패리티 검사기의.
| 4 비트 수신 데이터 WXYP | 짝수 패리티 검사 비트 E |
|---|---|
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 1 |
| 0011 | 0 |
| 0100 | 1 |
| 0101 | 0 |
| 0110 | 0 |
| 0111 | 1 |
| 1000 | 1 |
| 1001 | 0 |
| 1010 년 | 0 |
| 1011 | 1 |
| 1100 년 | 0 |
| 1101 | 1 |
| 1110 년 | 1 |
| 1111 년 | 0 |
위의 Truth 테이블에서 수신 된 데이터에 홀수 개의 1이 존재할 때 짝수 패리티 검사 비트 값이 '1'임을 알 수 있습니다. 즉, 짝수 패리티 검사 비트의 부울 함수는odd function. Exclusive-OR 함수는이 조건을 충족합니다. 따라서 우리는 직접 작성할 수 있습니다Boolean function 짝수 패리티 검사 비트의
$$E=W \oplus X \oplus Y \oplus P$$
다음 그림은 circuit diagram 패리티 검사기의.

이 회로는 세 가지로 구성됩니다. Exclusive-OR gates각각 두 개의 입력이 있습니다. 첫 번째 레벨 게이트는 다음과 같은 출력을 생성합니다.$W \oplus X$ & $Y \oplus P$. 두 번째 레벨에있는 Exclusive-OR 게이트는 다음과 같은 출력을 생성합니다.$W \oplus X \oplus Y \oplus P$
홀수 패리티 검사기
3 비트 이진 입력을 가정하면 WXY는 홀수 패리티 비트 P와 함께 전송됩니다. 따라서 결과 단어 (데이터)에는 4 비트가 포함되며, 이는 홀수 패리티 검사기의 입력으로 수신됩니다.
그것은 생성 odd parity check bit, E. 수신 된 데이터에 홀수의 1이 포함 된 경우이 비트는 0이됩니다. 이는 수신 된 데이터에 오류가 없음을 의미합니다. 이 홀수 패리티 검사 비트는 수신 된 데이터에 1이 짝수 인 경우 1이됩니다. 이는 수신 된 데이터에 오류가 있음을 의미합니다.
홀수 패리티 검사기를 구현하려면 짝수 패리티 검사기와 동일한 절차를 따르십시오. 그만큼circuit diagram 다음 그림은 홀수 패리티 검사기입니다.

위의 회로도는 첫 번째 레벨의 Ex-OR 게이트와 두 번째 레벨의 Ex-NOR 게이트로 구성됩니다. 홀수 패리티는 짝수 패리티와 정반대이므로 짝수 패리티 검사기의 출력에 인버터를 배치 할 수 있습니다. 이 경우 첫 번째, 두 번째 및 세 번째 레벨에는 각각 두 개의 Ex-OR 게이트, 하나의 Ex-OR 게이트 및 하나의 인버터가 포함됩니다.
이진 가산기
가장 기본적인 산술 연산은 덧셈입니다. 두 개의 이진수를 더하는 회로는Binary adder. 먼저 2 비트를 더하는 가산기를 구현해 보겠습니다.
반가산기
Half adder는 두 개의 이진수 A와 B를 더하는 조합 회로입니다. single bit. 두 개의 출력 합계, S 및 캐리, C를 생성합니다.
그만큼 Truth table 반가산기의 값은 아래와 같습니다.
| 입력 | 출력 | ||
|---|---|---|---|
| ㅏ | 비 | 씨 | 에스 |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
두 비트를 더하면 결과 합계는 10 진수로 0에서 2까지의 값을 가질 수 있습니다. 이진수로 단일 비트로 십진수 0과 1을 나타낼 수 있습니다. 그러나 우리는 이진수로 단일 비트로 십진수 2를 나타낼 수 없습니다. 그래서 우리는 그것을 이진으로 표현하기 위해 2 비트가 필요합니다.
S는 최하위 비트 및 캐리이고, C는 결과 합계의 최상위 비트입니다. 처음 세 가지 입력 조합의 경우 carry, C는 0이고 S의 값은 0 또는 1이됩니다.number of ones입력에 존재합니다. 그러나 마지막 입력 조합의 경우 결과 합이 2이기 때문에 C는 1이고 합은 S가 0입니다.
Truth 테이블에서 직접 작성할 수 있습니다. Boolean functions 각 출력에 대해
$$S=A \oplus B$$
$C=AB$
2 입력 Ex-OR 게이트와 2 입력 AND 게이트로 위의 기능을 구현할 수 있습니다. 그만큼circuit diagram 반가산기의 값은 다음 그림과 같습니다.

위의 회로에서 두 개의 입력 Ex-OR 게이트와 두 개의 입력 AND 게이트는 각각 합계, S 및 캐리, C를 생성합니다. 따라서 Half-adder는 2 비트의 추가를 수행합니다.
완전 가산기
완전 가산기는 조합 회로로, addition of three bitsA, B 및 C 에서 . 여기서 A와 B는 두 개의 병렬 유효 비트이고 C in 은 이전 단계에서 생성 된 캐리 비트입니다. 이 Full adder는 또한 Half adder와 유사한 두 개의 출력 합계, S & carry, C out 을 생성합니다.
그만큼 Truth table Full adder의 값은 아래와 같습니다.
| 입력 | 출력 | |||
|---|---|---|---|---|
| A | B | Cin | Cout | S |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
3 비트를 더하면 결과 합계는 10 진수로 0에서 3까지의 값을 가질 수 있습니다. 이진수로 단일 비트로 십진수 0과 1을 나타낼 수 있습니다. 그러나 우리는 이진수로 된 단일 비트로 10 진수 2와 3을 나타낼 수 없습니다. 그래서 우리는 이진법으로 두 십진수를 표현하기 위해 두 비트가 필요합니다.
S는 최하위 비트이고 수행하고, C out 은 결과 합계의 최상위 비트입니다. 진리표의 모든 입력 조합에 대한 출력 값을 채우는 것은 쉽습니다. 그냥 세어number of ones입력에 존재하고 출력에 동등한 이진수를 씁니다. C in 이 0이면 전체 가산기 진리표는 반가산기 진리표와 동일합니다.
우리는 다음을 얻을 것입니다 Boolean functions 단순화 후 각 출력에 대해.
$$S=A \oplus B \oplus C_{in}$$
$c_{out} = AB + \left ( A \oplus B \right )c_{in}$
입력에 홀수의 1이있을 때 합계 S는 1과 같습니다. Ex-OR 게이트가 홀수 함수 인 출력을 생성한다는 것을 알고 있습니다. 따라서 합계 S를 생성하기 위해 2 개의 2 입력 Ex-OR 게이트 또는 1 개의 3 입력 Ex-OR 게이트를 사용할 수 있습니다. 2 개의 2 입력 AND 게이트와 1 개의 OR 게이트를 사용하여 carry, C out 을 구현할 수 있습니다 . 그만큼circuit diagram Full adder의 값은 다음 그림과 같습니다.
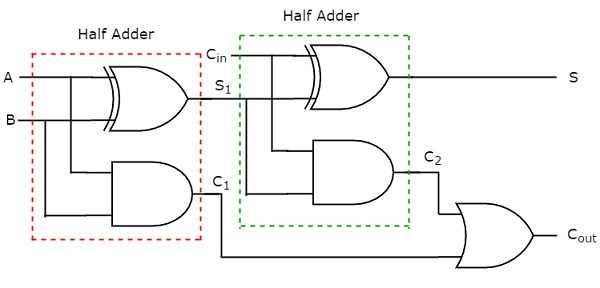
이 가산기는 다음과 같이 호출됩니다. Full adder하나의 Full adder를 구현하려면 두 개의 Half adder와 하나의 OR 게이트가 필요하기 때문입니다. C in 이 0이면 Full adder는 Half adder가됩니다. 위의 회로도 또는 Full adder 출력의 Boolean 함수에서 쉽게 확인할 수 있습니다.
4 비트 이진 가산기
4 비트 이진 가산기는 다음을 수행합니다. addition of two 4-bit numbers. 4 비트 이진수를 보자$A=A_{3}A_{2}A_{1}A_{0}$ 과 $B= B_{3}B_{2}B_{1}B_{0}$. 다음 두 가지 방법 중 하나로 4 비트 이진 가산기를 구현할 수 있습니다.
두 개의 최하위 비트를 추가하려면 하나의 절반 가산기를 사용하고 세 개의 상위 비트를 추가하려면 세 개의 전체 가산기를 사용하십시오.
균일 성을 위해 4 개의 완전 가산기를 사용합니다. 초기 carry C in 은 0이므로 최하위 비트를 추가하는 데 사용되는 Full adder는 Half adder가됩니다.
당분간 우리는 두 번째 접근 방식을 고려했습니다. 그만큼block diagram 4 비트 이진 가산기의 그림은 다음과 같습니다.

여기에서 4 개의 전체 가산기가 계단식으로 연결됩니다. 각 전체 가산기는 두 개의 병렬 입력 A 및 B의 각 비트를 가져옵니다. 하나의 전체 가산기의 캐리 출력은 후속 고차 전체 가산기의 캐리 입력이됩니다. 이 4 비트 이진 가산기는 최대 5 비트를 갖는 결과 합계를 생성합니다. 따라서 마지막 단계에서 수행하면 전체 가산기가 MSB가됩니다.
이런 식으로 필요한 수의 전체 가산기를 계단식으로 연결하여 고차 이진 가산기를 구현할 수 있습니다. 이 바이너리 가산기는 다음과 같이 불립니다.ripple carry (binary) adder 캐리가 한 단계에서 다음 단계로 전파되기 때문입니다.
이진 감산기
두 이진수를 빼는 회로는 다음과 같이 알려져 있습니다. Binary subtractor. Binary subtractor는 다음 두 가지 방법으로 구현할 수 있습니다.
- 캐스케이드 전체 감산기
- 2의 보수 방법
첫 번째 방법에서는 'n'전체 감산기를 계단식으로 연결하여 n 비트 이진 감산기를 얻습니다. 따라서 먼저 Half adder & Full adder와 유사한 Half subtractor와 Full subtractor를 구현할 수 있습니다. 그런 다음 'n'전체 감산기를 계단식으로 연결하여 n 비트 이진 감산기를 구현할 수 있습니다. 그래서, 우리는 두 이진수의 이진수 덧셈과 뺄셈을 위해 두 개의 개별 회로를 갖게 될 것입니다.
두 번째 방법에서는 두 번째 입력에서 일부 수정을 수행하여 두 이진수를 뺄 때 동일한 이진 가산기를 사용할 수 있습니다. 따라서 내부적으로 이진 덧셈 연산이 발생하지만 출력은 결과 뺄셈입니다.
두 이진수 A와 B의 빼기는 다음과 같이 쓸 수 있습니다.
$$A-B = A+\left ( {2}'s \: compliment \: of \: B \right )$$
$\Rightarrow A-B = A+\left ( {1}'s \: compliment \: of \: B \right )+1$
4 비트 이진 감산기
4 비트 이진 감산기는 다음을 생성합니다. subtraction of two 4-bit numbers. 4 비트 이진수를 보자,$A=A_{3}A_{2}A_{1}A_{0}$ 과 $B= B_{3}B_{2}B_{1}B_{0}$. 내부적으로 4 비트 이진 감산기의 작동은 4 비트 이진 가산기의 작동과 유사합니다. 이진수 A의 일반 비트, 이진수 B의 보완 비트 및 초기 캐리 (빌려), C in 을 1로 4 비트 이진 가산기에 적용하면 4 비트 이진 감산기가됩니다. 그만큼block diagram 4 비트 이진 감산기의 그림은 다음과 같습니다.

이 4 비트 이진 감산기는 최대 5 비트를 갖는 출력을 생성합니다. 이진수 A가 이진수 B보다 크면 출력의 MSB는 0이고 나머지 비트는 AB의 크기를 유지합니다. 이진수 A가 이진수 B보다 작 으면 출력의 MSB는 1입니다. 따라서 AB의 크기를 얻기 위해 출력의 2의 보수를 취하십시오.
이런 식으로 필요한 수정을 통해 필요한 수의 전체 가산기를 계단식으로 연결하여 고차 이진 감산기를 구현할 수 있습니다.
이진 가산기 / 감산기
언제든지 두 이진수의 더하기 또는 빼기를 수행하는 데 사용할 수있는 회로는 다음과 같이 알려져 있습니다. Binary Adder / subtractor. 이진 가산기와 이진 감산기 모두 계단식으로 연결된 전체 가산기 세트를 포함합니다. 이진수 A의 입력 비트는 이진 가산기와 이진 감산기 모두에 직접 적용됩니다.
이진 가산기와 이진 감산기에있는 완전 가산기의 입력에는 두 가지 차이점이 있습니다.
이진수 B의 입력 비트는 이진 가산기의 전체 가산기에 직접 적용되는 반면, 이진수 B의 보완 비트는 이진 감산기의 전체 가산기에 적용됩니다.
초기 캐리, C 0 = 0은 4 비트 이진 가산기에서 적용되는 반면, 초기 캐리 (차용), C 0 = 1은 4 비트 이진 감산기에서 적용됩니다.
우리는 2-input Ex-OR gate다른 입력이 0 일 때 첫 번째 입력과 동일한 출력을 생성합니다. 마찬가지로 다른 입력이 1 일 때 첫 번째 입력을 보완하는 출력을 생성합니다.
따라서 이진수 B의 입력 비트를 2 입력 Ex-OR 게이트에 적용 할 수 있습니다. 이 모든 Ex-OR 게이트에 대한 다른 입력은 C 0 입니다. 따라서 C 0 의 값을 기반으로 Ex-OR 게이트는 이진수 B의 일반 또는 보완 비트를 생성합니다.
4 비트 이진 가산기 / 감산기
4 비트 이진 가산기 / 감산기는 초기 캐리 또는 빌리기 값 0을 기반으로 두 개의 4 비트 숫자를 더하거나 뺍니다 . 4 비트 이진수를 보자$A=A_{3}A_{2}A_{1}A_{0}$ 과 $B= B_{3}B_{2}B_{1}B_{0}$. 4 비트 이진 가산기 / 감산기의 작동은 4 비트 이진 가산기 및 4 비트 이진 감산기의 작동과 유사합니다.
이진수 A와 B의 일반 비트와 초기 캐리 또는 빌리, C 0 을 외부에서 4 비트 이진 가산기로 적용합니다. 그만큼block diagram 4 비트 이진 가산기 / 감산기의 그림은 다음과 같습니다.
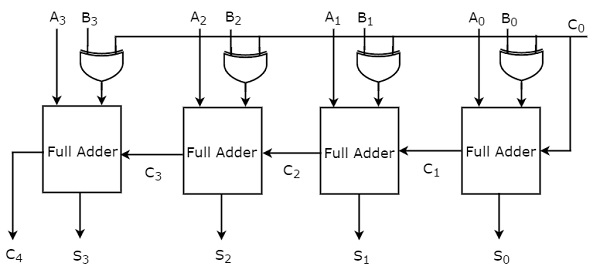
초기 캐리, 0 이 0이면 각 완전 가산기는 이진수 A와 B의 일반 비트를 얻습니다. 따라서 4 비트 이진 가산기 / 감산기는 출력을 생성합니다.addition of two binary numbers A & B.
초기 차용인 경우 0 이 1이면 각 완전 가산기는 이진수 A의 일반 비트와 이진수 B의 보완 비트를 얻습니다. 따라서 4 비트 이진 가산기 / 감산기는 출력을 생성합니다.subtraction of two binary numbers A & B.
따라서 추가 Ex-OR 게이트의 도움으로 동일한 회로를 두 이진수의 더하기와 빼기에 모두 사용할 수 있습니다.
Decoder'n'개의 입력 라인과 최대 2n 개의 출력 라인을 가진 조합 회로입니다 . 이러한 출력 중 하나는 디코더가 활성화 된 경우 존재하는 입력 조합에 따라 활성 High가됩니다. 이는 디코더가 특정 코드를 감지 함을 의미합니다. 디코더의 출력은min terms 사용 가능한 경우 'n'입력 변수 (라인) 중.
2 ~ 4 디코더
2-4 디코더에 두 개의 입력 A 1 & A 0 과 네 개의 출력 Y 3 , Y 2 , Y 1 & Y 0이 있습니다. 그만큼block diagram 2 ~ 4 디코더의 구성은 다음 그림에 나와 있습니다.

이 4 개의 출력 중 하나는 활성화 될 때 각 입력 조합에 대해 '1'이되고 E는 '1'입니다. 그만큼Truth table 2 ~ 4 개의 디코더가 아래에 나와 있습니다.
| 활성화 | 입력 | 출력 | ||||
|---|---|---|---|---|---|---|
| E | A1 | A0 | Y3 | Y2 | Y1 | Y0 |
| 0 | 엑스 | 엑스 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 |
진실 테이블에서 우리는 Boolean functions 각 출력에 대해
$$Y_{3}=E.A_{1}.A_{0}$$
$$ Y_{2}=E.A_{1}.{A_{0}}'$$
$$ Y_{1}=E.{A_{1}}'.A_{0}$$
$$ Y_{0}=E.{A_{1}}'.{A_{0}}'$$
각 출력에는 하나의 제품 용어가 있습니다. 따라서 총 4 개의 제품 용어가 있습니다. 각각 3 개의 입력과 2 개의 인버터가있는 4 개의 AND 게이트를 사용하여이 4 가지 제품 용어를 구현할 수 있습니다. 그만큼circuit diagram 2 ~ 4 디코더의 구성은 다음 그림에 나와 있습니다.

따라서 2-4 디코더의 출력은 min terms두 개의 입력 변수 A 1 & A 0의 활성화시 E는 1과 같습니다. 활성화하면 E가 0이면 디코더의 모든 출력이 0이됩니다.
유사하게, 3-8 디코더는 3 개의 입력 변수 A 2 , A 1 & A 0 의 8 분 항을 생성하고 4-16 디코더는 4 개의 입력 변수 A 3 , A 2 , A 1 & A 0의 16 분 항을 생성합니다 .
고차 디코더 구현
이제 하위 디코더를 사용하여 다음 두 개의 상위 디코더를 구현해 보겠습니다.
- 3 ~ 8 디코더
- 4 ~ 16 디코더
3 ~ 8 디코더
이 섹션에서는 3 to 8 decoder using 2 to 4 decoders. 우리는 2-4 디코더에 두 개의 입력, A 1 & A 0 및 네 개의 출력, Y 3 ~ Y 0이 있다는 것을 알고 있습니다. 반면 3 ~ 8 디코더에는 3 개의 입력 A 2 , A 1 & A 0 및 8 개의 출력, Y 7 ~ Y 0이 있습니다.
다음 공식을 사용하여 고차 디코더를 구현하는 데 필요한 저차 디코더의 수를 찾을 수 있습니다.
$$Required \: number \: of \: lower \: order \: decoders=\frac{m_{2}}{m_{1}}$$
어디,
$m_{1}$ 하위 디코더의 출력 수입니다.
$m_{2}$ 고차 디코더의 출력 수입니다.
여기, $m_{1}$ = 4 및 $m_{2}$ = 8. 위 공식에서이 두 값을 대입합니다.
$$Required \: number \: of \: 2 \: to \: 4 \: decoders=\frac{8}{4}=2$$
따라서 하나의 3 ~ 8 디코더를 구현하려면 2 ~ 4 개의 디코더가 필요합니다. 그만큼block diagram 2 ~ 4 개의 디코더를 사용하는 3 ~ 8 개의 디코더가 다음 그림에 나와 있습니다.

병렬 입력 A 1 및 A 0 은 각 2 ~ 4 디코더에 적용됩니다. 입력 A 2 의 보완은 출력 Y 3 ~ Y 0 을 얻기 위해 하위 2 ~ 4 디코더의 E에 연결됩니다 . 이것들은lower four min terms. 입력 A 2 는 출력 Y 7 ~ Y 4 를 얻기 위해 상위 2 ~ 4 디코더의 Enable, E에 직접 연결됩니다 . 이것들은higher four min terms.
4 ~ 16 디코더
이 섹션에서는 4 to 16 decoder using 3 to 8 decoders. 3 ~ 8 디코더에는 3 개의 입력 A 2 , A 1 & A 0 과 8 개의 출력, Y 7 ~ Y 0이 있습니다. 반면, 4 ~ 16 디코더에는 4 개의 입력 A 3 , A 2 , A 1 & A 0 및 16 개의 출력, Y 15 ~ Y 0
필요한 하위 디코더 수를 찾기 위해 다음 공식을 알고 있습니다.
$$Required \: number \: of \: lower \: order \: decoders=\frac{m_{2}}{m_{1}}$$
대용품, $m_{1}$ = 8 및 $m_{2}$ = 위의 공식에서 16.
$$Required \: number \: of \: 3 \: to \: 8 decoders=\frac{16}{8}=2$$
따라서 하나의 4-16 디코더를 구현하려면 2 개의 3-8 디코더가 필요합니다. 그만큼block diagram 3 ~ 8 개의 디코더를 사용하는 4 ~ 16 개의 디코더가 다음 그림에 나와 있습니다.

병렬 입력 A 2 , A 1 & A 0 은 각 3 ~ 8 디코더에 적용됩니다. 입력의 보완, A3는 출력, Y 7 ~ Y 0 을 얻기 위해 하위 3 ~ 8 디코더의 E에 연결됩니다 . 이것들은lower eight min terms. 입력 A 3 은 출력 Y 15 ~ Y 8 을 얻기 위해 상위 3 ~ 8 디코더의 Enable, E에 직접 연결됩니다 . 이것들은higher eight min terms.
안 EncoderDecoder의 역 동작을 수행하는 조합 회로입니다. 최대 2n 개의 입력 라인과 'n'개의 출력 라인이 있습니다. 입력에 해당하는 이진 코드를 생성하며 이는 활성 High입니다. 따라서 인코더는 'n'비트로 2n 개의 입력 라인을 인코딩 합니다. 인코더에서 활성화 신호를 나타내는 것은 선택 사항입니다.
4 ~ 2 인코더
4 대 2 인코더에는 4 개의 입력 Y 3 , Y 2 , Y 1 & Y 0 과 2 개의 출력 A 1 & A 0이 있습니다. 그만큼block diagram 다음 그림은 4 ~ 2 인코더 중 하나입니다.

출력에서 각각의 이진 코드를 얻기 위해 언제든지이 4 개의 입력 중 하나만 '1'이 될 수 있습니다. 그만큼Truth table 4 ~ 2 엔코더의 그림은 아래와 같습니다.
| 입력 | 출력 | ||||
|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
진실 테이블에서 우리는 Boolean functions 각 출력에 대해
$$A_{1}=Y_{3}+Y_{2}$$
$$A_{0}=Y_{3}+Y_{1}$$
두 개의 입력 OR 게이트를 사용하여 위의 두 가지 부울 함수를 구현할 수 있습니다. 그만큼circuit diagram 4 ~ 2 엔코더의 구성은 다음 그림과 같습니다.

위의 회로도에는 두 개의 OR 게이트가 있습니다. 이 OR 게이트는 4 개의 입력을 2 비트로 인코딩합니다.
8 진법 인코더
Octal to binary 인코더에는 8 개의 입력, Y 7 ~ Y 0 및 3 개의 출력 A 2 , A 1 & A 0이 있습니다. 8 진법 인코더는 8 ~ 3 인코더 일뿐입니다. 그만큼block diagram 다음 그림은 8 진수에서 2 진 인코더로의 변환을 보여줍니다.
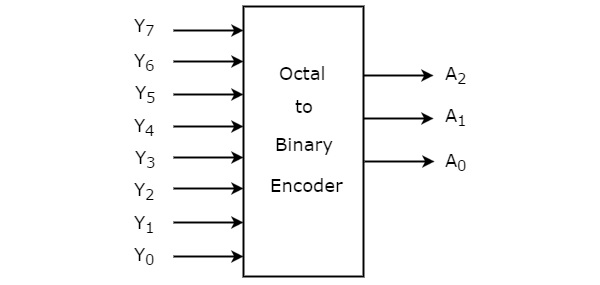
언제든지 각 이진 코드를 얻기 위해 8 개의 입력 중 하나만 '1'이 될 수 있습니다. 그만큼Truth table 8 진수에서 바이너리 인코더로의 값은 아래와 같습니다.
| 입력 | 출력 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 | A2 | A1 | A0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
From Truth table, we can write the Boolean functions for each output as
$$A_{2}=Y_{7}+Y_{6}+Y_{5}+Y_{4}$$
$$A_{1}=Y_{7}+Y_{6}+Y_{3}+Y_{2}$$
$$A_{0}=Y_{7}+Y_{5}+Y_{3}+Y_{1}$$
We can implement the above Boolean functions by using four input OR gates. The circuit diagram of octal to binary encoder is shown in the following figure.

The above circuit diagram contains three 4-input OR gates. These OR gates encode the eight inputs with three bits.
Drawbacks of Encoder
Following are the drawbacks of normal encoder.
There is an ambiguity, when all outputs of encoder are equal to zero. Because, it could be the code corresponding to the inputs, when only least significant input is one or when all inputs are zero.
If more than one input is active High, then the encoder produces an output, which may not be the correct code. For example, if both Y3 and Y6 are ‘1’, then the encoder produces 111 at the output. This is neither equivalent code corresponding to Y3, when it is ‘1’ nor the equivalent code corresponding to Y6, when it is ‘1’.
So, to overcome these difficulties, we should assign priorities to each input of encoder. Then, the output of encoder will be the (binary) code corresponding to the active High input(s), which has higher priority. This encoder is called as priority encoder.
Priority Encoder
A 4 to 2 priority encoder has four inputs Y3, Y2, Y1 & Y0 and two outputs A1 & A0. Here, the input, Y3 has the highest priority, whereas the input, Y0 has the lowest priority. In this case, even if more than one input is ‘1’ at the same time, the output will be the (binary) code corresponding to the input, which is having higher priority.
We considered one more output, V in order to know, whether the code available at outputs is valid or not.
If at least one input of the encoder is ‘1’, then the code available at outputs is a valid one. In this case, the output, V will be equal to 1.
If all the inputs of encoder are ‘0’, then the code available at outputs is not a valid one. In this case, the output, V will be equal to 0.
The Truth table of 4 to 2 priority encoder is shown below.
| Inputs | Outputs | |||||
|---|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 | V |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | x | 0 | 1 | 1 |
| 0 | 1 | x | x | 1 | 0 | 1 |
| 1 | x | x | x | 1 | 1 | 1 |
Use 4 variable K-maps for getting simplified expressions for each output.
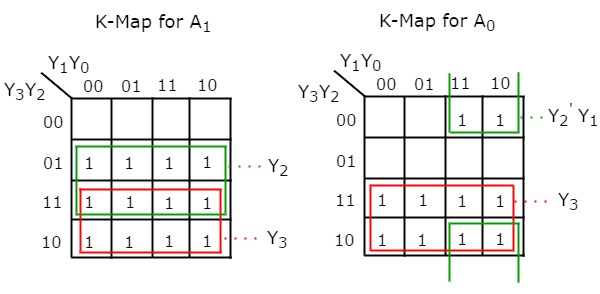
The simplified Boolean functions are
$$A_{1}=Y_{3}+Y_{2}$$
$A_{0}=Y_{3}+{Y_{2}}'Y_{1}$
Similarly, we will get the Boolean function of output, V as
$$V=Y_{3}+Y_{2}+Y_{1}+Y_{0}$$
We can implement the above Boolean functions using logic gates. The circuit diagram of 4 to 2 priority encoder is shown in the following figure.

The above circuit diagram contains two 2-input OR gates, one 4-input OR gate, one 2input AND gate & an inverter. Here AND gate & inverter combination are used for producing a valid code at the outputs, even when multiple inputs are equal to ‘1’ at the same time. Hence, this circuit encodes the four inputs with two bits based on the priority assigned to each input.
Multiplexer is a combinational circuit that has maximum of 2n data inputs, ‘n’ selection lines and single output line. One of these data inputs will be connected to the output based on the values of selection lines.
Since there are ‘n’ selection lines, there will be 2n possible combinations of zeros and ones. So, each combination will select only one data input. Multiplexer is also called as Mux.
4x1 Multiplexer
4x1 Multiplexer has four data inputs I3, I2, I1 & I0, two selection lines s1 & s0 and one output Y. The block diagram of 4x1 Multiplexer is shown in the following figure.

One of these 4 inputs will be connected to the output based on the combination of inputs present at these two selection lines. Truth table of 4x1 Multiplexer is shown below.
| Selection Lines | Output | |
|---|---|---|
| S1 | S0 | Y |
| 0 | 0 | I0 |
| 0 | 1 | I1 |
| 1 | 0 | I2 |
| 1 | 1 | I3 |
From Truth table, we can directly write the Boolean function for output, Y as
$$Y={S_{1}}'{S_{0}}'I_{0}+{S_{1}}'S_{0}I_{1}+S_{1}{S_{0}}'I_{2}+S_{1}S_{0}I_{3}$$
We can implement this Boolean function using Inverters, AND gates & OR gate. The circuit diagram of 4x1 multiplexer is shown in the following figure.

We can easily understand the operation of the above circuit. Similarly, you can implement 8x1 Multiplexer and 16x1 multiplexer by following the same procedure.
Implementation of Higher-order Multiplexers.
Now, let us implement the following two higher-order Multiplexers using lower-order Multiplexers.
- 8x1 Multiplexer
- 16x1 Multiplexer
8x1 Multiplexer
In this section, let us implement 8x1 Multiplexer using 4x1 Multiplexers and 2x1 Multiplexer. We know that 4x1 Multiplexer has 4 data inputs, 2 selection lines and one output. Whereas, 8x1 Multiplexer has 8 data inputs, 3 selection lines and one output.
So, we require two 4x1 Multiplexers in first stage in order to get the 8 data inputs. Since, each 4x1 Multiplexer produces one output, we require a 2x1 Multiplexer in second stage by considering the outputs of first stage as inputs and to produce the final output.
Let the 8x1 Multiplexer has eight data inputs I7 to I0, three selection lines s2, s1 & s0 and one output Y. The Truth table of 8x1 Multiplexer is shown below.
| Selection Inputs | Output | ||
|---|---|---|---|
| S2 | S1 | S0 | Y |
| 0 | 0 | 0 | I0 |
| 0 | 0 | 1 | I1 |
| 0 | 1 | 0 | I2 |
| 0 | 1 | 1 | I3 |
| 1 | 0 | 0 | I4 |
| 1 | 0 | 1 | I5 |
| 1 | 1 | 0 | I6 |
| 1 | 1 | 1 | I7 |
We can implement 8x1 Multiplexer using lower order Multiplexers easily by considering the above Truth table. The block diagram of 8x1 Multiplexer is shown in the following figure.

The same selection lines, s1 & s0 are applied to both 4x1 Multiplexers. The data inputs of upper 4x1 Multiplexer are I7 to I4 and the data inputs of lower 4x1 Multiplexer are I3 to I0. Therefore, each 4x1 Multiplexer produces an output based on the values of selection lines, s1 & s0.
The outputs of first stage 4x1 Multiplexers are applied as inputs of 2x1 Multiplexer that is present in second stage. The other selection line, s2 is applied to 2x1 Multiplexer.
If s2 is zero, then the output of 2x1 Multiplexer will be one of the 4 inputs I3 to I0 based on the values of selection lines s1 & s0.
If s2 is one, then the output of 2x1 Multiplexer will be one of the 4 inputs I7 to I4 based on the values of selection lines s1 & s0.
Therefore, the overall combination of two 4x1 Multiplexers and one 2x1 Multiplexer performs as one 8x1 Multiplexer.
16x1 Multiplexer
In this section, let us implement 16x1 Multiplexer using 8x1 Multiplexers and 2x1 Multiplexer. We know that 8x1 Multiplexer has 8 data inputs, 3 selection lines and one output. Whereas, 16x1 Multiplexer has 16 data inputs, 4 selection lines and one output.
So, we require two 8x1 Multiplexers in first stage in order to get the 16 data inputs. Since, each 8x1 Multiplexer produces one output, we require a 2x1 Multiplexer in second stage by considering the outputs of first stage as inputs and to produce the final output.
Let the 16x1 Multiplexer has sixteen data inputs I15 to I0, four selection lines s3 to s0 and one output Y. The Truth table of 16x1 Multiplexer is shown below.
| Selection Inputs | Output | |||
|---|---|---|---|---|
| S3 | S2 | S1 | S0 | Y |
| 0 | 0 | 0 | 0 | I0 |
| 0 | 0 | 0 | 1 | I1 |
| 0 | 0 | 1 | 0 | I2 |
| 0 | 0 | 1 | 1 | I3 |
| 0 | 1 | 0 | 0 | I4 |
| 0 | 1 | 0 | 1 | I5 |
| 0 | 1 | 1 | 0 | I6 |
| 0 | 1 | 1 | 1 | I7 |
| 1 | 0 | 0 | 0 | I8 |
| 1 | 0 | 0 | 1 | I9 |
| 1 | 0 | 1 | 0 | I10 |
| 1 | 0 | 1 | 1 | I11 |
| 1 | 1 | 0 | 0 | I12 |
| 1 | 1 | 0 | 1 | I13 |
| 1 | 1 | 1 | 0 | I14 |
| 1 | 1 | 1 | 1 | I15 |
We can implement 16x1 Multiplexer using lower order Multiplexers easily by considering the above Truth table. The block diagram of 16x1 Multiplexer is shown in the following figure.

The same selection lines, s2, s1 & s0 are applied to both 8x1 Multiplexers. The data inputs of upper 8x1 Multiplexer are I15 to I8 and the data inputs of lower 8x1 Multiplexer are I7 to I0. Therefore, each 8x1 Multiplexer produces an output based on the values of selection lines, s2, s1 & s0.
The outputs of first stage 8x1 Multiplexers are applied as inputs of 2x1 Multiplexer that is present in second stage. The other selection line, s3 is applied to 2x1 Multiplexer.
If s3 is zero, then the output of 2x1 Multiplexer will be one of the 8 inputs Is7 to I0 based on the values of selection lines s2, s1 & s0.
If s3 is one, then the output of 2x1 Multiplexer will be one of the 8 inputs I15 to I8 based on the values of selection lines s2, s1 & s0.
Therefore, the overall combination of two 8x1 Multiplexers and one 2x1 Multiplexer performs as one 16x1 Multiplexer.
De-Multiplexer is a combinational circuit that performs the reverse operation of Multiplexer. It has single input, ‘n’ selection lines and maximum of 2n outputs. The input will be connected to one of these outputs based on the values of selection lines.
Since there are ‘n’ selection lines, there will be 2n possible combinations of zeros and ones. So, each combination can select only one output. De-Multiplexer is also called as De-Mux.
1x4 De-Multiplexer
1x4 De-Multiplexer has one input I, two selection lines, s1 & s0 and four outputs Y3, Y2, Y1 &Y0. The block diagram of 1x4 De-Multiplexer is shown in the following figure.

The single input ‘I’ will be connected to one of the four outputs, Y3 to Y0 based on the values of selection lines s1 & s0. The Truth table of 1x4 De-Multiplexer is shown below.
| Selection Inputs | Outputs | ||||
|---|---|---|---|---|---|
| S1 | S0 | Y3 | Y2 | Y1 | Y0 |
| 0 | 0 | 0 | 0 | 0 | I |
| 0 | 1 | 0 | 0 | I | 0 |
| 1 | 0 | 0 | I | 0 | 0 |
| 1 | 1 | I | 0 | 0 | 0 |
From the above Truth table, we can directly write the Boolean functions for each output as
$$Y_{3}=s_{1}s_{0}I$$
$$Y_{2}=s_{1}{s_{0}}'I$$
$$Y_{1}={s_{1}}'s_{0}I$$
$$Y_{0}={s_1}'{s_{0}}'I$$
We can implement these Boolean functions using Inverters & 3-input AND gates. The circuit diagram of 1x4 De-Multiplexer is shown in the following figure.

We can easily understand the operation of the above circuit. Similarly, you can implement 1x8 De-Multiplexer and 1x16 De-Multiplexer by following the same procedure.
Implementation of Higher-order De-Multiplexers
Now, let us implement the following two higher-order De-Multiplexers using lower-order De-Multiplexers.
- 1x8 De-Multiplexer
- 1x16 De-Multiplexer
1x8 De-Multiplexer
In this section, let us implement 1x8 De-Multiplexer using 1x4 De-Multiplexers and 1x2 De-Multiplexer. We know that 1x4 De-Multiplexer has single input, two selection lines and four outputs. Whereas, 1x8 De-Multiplexer has single input, three selection lines and eight outputs.
So, we require two 1x4 De-Multiplexers in second stage in order to get the final eight outputs. Since, the number of inputs in second stage is two, we require 1x2 DeMultiplexer in first stage so that the outputs of first stage will be the inputs of second stage. Input of this 1x2 De-Multiplexer will be the overall input of 1x8 De-Multiplexer.
Let the 1x8 De-Multiplexer has one input I, three selection lines s2, s1 & s0 and outputs Y7 to Y0. The Truth table of 1x8 De-Multiplexer is shown below.
| Selection Inputs | Outputs | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| s2 | s1 | s0 | Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | I |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | I | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | I | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | I | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | I | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | I | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
We can implement 1x8 De-Multiplexer using lower order Multiplexers easily by considering the above Truth table. The block diagram of 1x8 De-Multiplexer is shown in the following figure.

The common selection lines, s1 & s0 are applied to both 1x4 De-Multiplexers. The outputs of upper 1x4 De-Multiplexer are Y7 to Y4 and the outputs of lower 1x4 De-Multiplexer are Y3 to Y0.
The other selection line, s2 is applied to 1x2 De-Multiplexer. If s2 is zero, then one of the four outputs of lower 1x4 De-Multiplexer will be equal to input, I based on the values of selection lines s1 & s0. Similarly, if s2 is one, then one of the four outputs of upper 1x4 DeMultiplexer will be equal to input, I based on the values of selection lines s1 & s0.
1x16 De-Multiplexer
In this section, let us implement 1x16 De-Multiplexer using 1x8 De-Multiplexers and 1x2 De-Multiplexer. We know that 1x8 De-Multiplexer has single input, three selection lines and eight outputs. Whereas, 1x16 De-Multiplexer has single input, four selection lines and sixteen outputs.
So, we require two 1x8 De-Multiplexers in second stage in order to get the final sixteen outputs. Since, the number of inputs in second stage is two, we require 1x2 DeMultiplexer in first stage so that the outputs of first stage will be the inputs of second stage. Input of this 1x2 De-Multiplexer will be the overall input of 1x16 De-Multiplexer.
Let the 1x16 De-Multiplexer has one input I, four selection lines s3, s2, s1 & s0 and outputs Y15 to Y0. The block diagram of 1x16 De-Multiplexer using lower order Multiplexers is shown in the following figure.
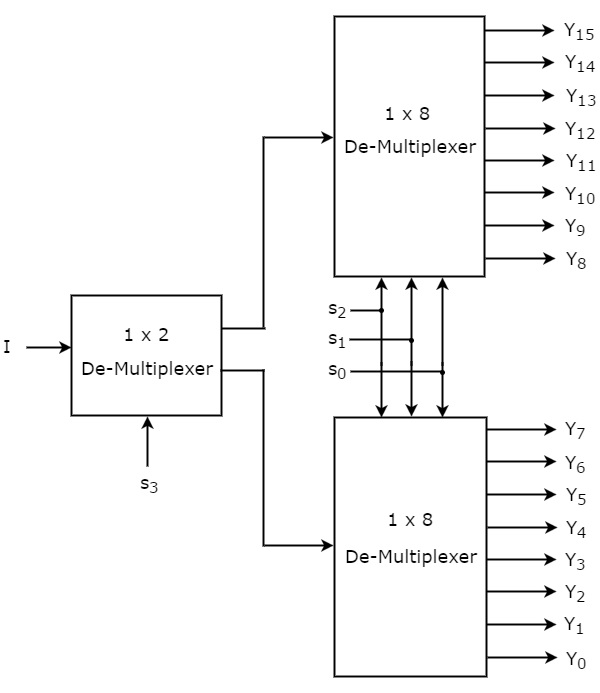
The common selection lines s2, s1 & s0 are applied to both 1x8 De-Multiplexers. The outputs of upper 1x8 De-Multiplexer are Y15 to Y8 and the outputs of lower 1x8 DeMultiplexer are Y7 to Y0.
다른 selection line, s31x2 De-Multiplexer에 적용됩니다. s 3 이 0이면 선택 라인 s 2 , s 1 & s 0 의 값에 따라 하위 1x8 디멀티플렉서의 8 개 출력 중 하나가 입력 I와 같습니다 . 마찬가지로, s3이 1이면 상위 1x8 디멀티플렉서의 8 개 출력 중 하나는 선택 라인 s 2 , s 1 & s 0 의 값을 기준으로 입력 I와 같습니다 .
프로그래밍 가능 논리 장치 (PLDs)집적 회로입니다. 여기에는 AND 게이트 배열과 OR 게이트 배열이 있습니다. 프로그래밍 가능한 기능이있는 어레이 유형에 따라 3 가지 종류의 PLD가 있습니다.
- 프로그래밍 가능한 읽기 전용 메모리
- 프로그래밍 가능 어레이 로직
- 프로그래밍 가능 논리 어레이
이러한 장치에 정보를 입력하는 과정을 programming. 기본적으로 사용자는 요구 사항에 따라 부울 기능을 구현하기 위해 이러한 장치 또는 IC를 전기적으로 프로그래밍 할 수 있습니다. 여기서 프로그래밍이라는 용어는 소프트웨어 프로그래밍이 아닌 하드웨어 프로그래밍을 의미합니다.
프로그래밍 가능 읽기 전용 메모리 (PROM)
ROM (Read Only Memory)은 바이너리 정보를 영구적으로 저장하는 메모리 장치입니다. 즉, 나중에 저장된 정보를 변경할 수 없습니다. ROM에 프로그래밍 가능한 기능이 있으면 다음과 같이 호출됩니다.Programmable ROM (PROM). 사용자는 PROM 프로그래머를 사용하여 이진 정보를 전기적으로 한 번 프로그래밍 할 수있는 유연성이 있습니다.
PROM은 고정 AND 어레이 및 프로그래밍 가능 OR 어레이를 가진 프로그래밍 가능한 논리 장치입니다. 그만큼block diagram PROM의 내용은 다음 그림과 같습니다.

여기서 AND 게이트의 입력은 프로그래밍 가능한 유형이 아닙니다. 따라서 각각 n 개의 입력을 갖는 2n 개의 AND 게이트를 사용하여 2n 개의 제품 항 을 생성해야합니다 . nx2 n 디코더 를 사용하여 이러한 제품 용어를 구현할 수 있습니다 . 따라서이 디코더는 'n'을 생성합니다.min terms.
여기서 OR 게이트의 입력은 프로그래밍 가능합니다. 즉, AND 게이트의 모든 출력이 각 OR 게이트에 입력으로 적용되기 때문에 필요한 제품 용어를 원하는만큼 프로그래밍 할 수 있습니다. 따라서 PROM의 출력은 다음과 같은 형식이됩니다.sum of min terms.
예
다음을 구현하겠습니다. Boolean functions PROM 사용.
$$A(X,Y,Z)=\sum m\left ( 5,6,7 \right )$$
$$B(X,Y,Z)=\sum m\left ( 3,5,6,7 \right )$$
주어진 두 함수는 최소 용어 형식의 합계이며 각 함수는 세 개의 변수 X, Y 및 Z를 갖습니다. 따라서이 두 함수를 생성하려면 3 ~ 8 디코더와 두 개의 프로그래밍 가능한 OR 게이트가 필요합니다. 해당PROM 다음 그림에 나와 있습니다.

여기에서 3 ~ 8 개의 디코더는 8 개의 최소 항을 생성합니다. 두 개의 프로그래밍 가능한 OR 게이트는 이러한 모든 최소 용어에 액세스 할 수 있습니다. 그러나 각 OR 게이트에 의해 각각의 부울 함수를 생성하기 위해 필요한 최소 항만 프로그래밍됩니다. 기호 'X'는 프로그래밍 가능한 연결에 사용됩니다.
프로그래밍 가능 어레이 로직 (PAL)
PAL은 Programmable AND array & fixed OR array를 가진 프로그램 가능한 논리 장치입니다. PAL의 장점은 프로그래밍 가능한 AND 게이트를 사용하여 모든 최소 항을 생성하는 대신 부울 함수의 필수 제품 항만 생성 할 수 있다는 것입니다. 그만큼block diagram PAL의 값은 다음 그림과 같습니다.

여기서 AND 게이트의 입력은 프로그래밍 가능합니다. 즉, 각 AND 게이트에는 정상 및 보완 변수 입력이 모두 있습니다. 따라서 요구 사항에 따라 이러한 입력을 프로그래밍 할 수 있습니다. 따라서 필요한 항목 만 생성 할 수 있습니다.product terms 이 AND 게이트를 사용하여.
여기서 OR 게이트의 입력은 프로그래밍 가능한 유형이 아닙니다. 따라서 각 OR 게이트에 대한 입력 수는 고정 유형입니다. 따라서 각 OR 게이트에 필요한 제품 용어를 입력으로 적용하십시오. 따라서 PAL의 출력은 다음과 같은 형식이됩니다.sum of products form.
예
다음을 구현하겠습니다. Boolean functions PAL 사용.
$$A=XY+X{Z}'$$
$$A=X{Y}'+Y{Z}'$$
주어진 두 기능은 제품 형태의 합계입니다. 각 부울 함수에는 두 가지 제품 용어가 있습니다. 따라서이 두 함수를 생성하려면 프로그래밍 가능한 AND 게이트 4 개와 고정 OR 게이트 2 개가 필요합니다. 해당PAL 다음 그림에 나와 있습니다.

그만큼 programmable AND gates변수의 정상 및 보완 입력 모두에 액세스 할 수 있습니다. 위 그림에서 입력 X,${X}'$, Y, ${Y}'$, Z 및 ${Z}'$, 각 AND 게이트의 입력에서 사용할 수 있습니다. 따라서 각 AND 게이트에서 하나의 제품 용어를 생성하기 위해 필요한 리터럴 만 프로그래밍하십시오. 기호 'X'는 프로그래밍 가능한 연결에 사용됩니다.
여기에서 OR 게이트의 입력은 고정 유형입니다. 따라서 필요한 제품 용어는 각각의 입력에 연결됩니다.OR gate. 따라서 OR 게이트는 각각의 부울 함수를 생성합니다. 상징물 '.' 고정 연결에 사용됩니다.
프로그래밍 가능 논리 어레이 (PLA)
PLA는 Programmable AND array & Programmable OR array를 모두 갖춘 프로그래밍 가능한 논리 장치입니다. 따라서 가장 유연한 PLD입니다. 그만큼block diagram PLA의 내용은 다음 그림과 같습니다.

여기서 AND 게이트의 입력은 프로그래밍 가능합니다. 즉, 각 AND 게이트에는 정상 및 보완 변수 입력이 모두 있습니다. 따라서 요구 사항에 따라 이러한 입력을 프로그래밍 할 수 있습니다. 따라서 필요한 항목 만 생성 할 수 있습니다.product terms 이 AND 게이트를 사용하여.
여기에서 OR 게이트의 입력도 프로그래밍 할 수 있습니다. 따라서 AND 게이트의 모든 출력이 각 OR 게이트에 입력으로 적용되므로 필요한 제품 용어를 원하는만큼 프로그래밍 할 수 있습니다. 따라서 PAL의 출력은 다음과 같은 형식이됩니다.sum of products form.
예
다음을 구현하겠습니다. Boolean functions PLA 사용.
$$A=XY+X{Z}'$$
$$B=X{Y}'+YZ+X{Z}'$$
주어진 두 기능은 제품 형태의 합계입니다. 주어진 부울 함수 A와 B에있는 제품 용어의 수는 각각 2 개와 3 개입니다. 하나의 제품 용어,${Z}'X$ 각 기능에서 공통입니다.
따라서이 두 기능을 생성하려면 프로그래밍 가능한 AND 게이트 4 개와 프로그래밍 가능한 OR 게이트 2 개가 필요합니다. 해당PLA 다음 그림에 나와 있습니다.
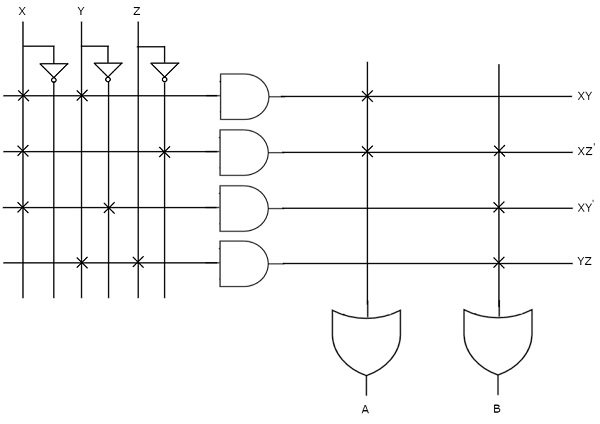
그만큼 programmable AND gates변수의 정상 및 보완 입력 모두에 액세스 할 수 있습니다. 위 그림에서 입력 X,${X}'$, Y, ${Y}'$, Z 및 ${Z}'$, 각 AND 게이트의 입력에서 사용할 수 있습니다. 따라서 각 AND 게이트에서 하나의 제품 용어를 생성하기 위해 필요한 리터럴 만 프로그래밍하십시오.
이러한 모든 제품 용어는 각각의 입력에서 사용할 수 있습니다. programmable OR gate. 그러나 각 OR 게이트에서 각각의 부울 함수를 생성하기 위해 필요한 제품 용어 만 프로그래밍하십시오. 기호 'X'는 프로그래밍 가능한 연결에 사용됩니다.
이전 장에서는 논리 게이트를 사용하여 다양한 조합 회로를 구현했습니다. NOT 게이트를 제외하고 나머지 모든 로직 게이트에는 최소 2 개의 입력과 단일 출력이 있습니다. 마찬가지로threshold gate 또한 적어도 하나의 입력과 하나의 출력 만 포함합니다.
또한 각 입력에 대한 각 가중치와 임계 값을 포함합니다. 이러한 가중치와 임계 값의 값은 유한 실수 일 수 있습니다.
임계 값 게이트의 기초
임계 값 게이트의 입력을 X 1 , X 2 , X 3 ,…, X n이라고 합니다. 이러한 입력의 해당 가중치는 W 1 , W 2 , W 3 ,…, W n 입니다. 그만큼symbol 임계 값 게이트의 값은 다음 그림에 나와 있습니다.
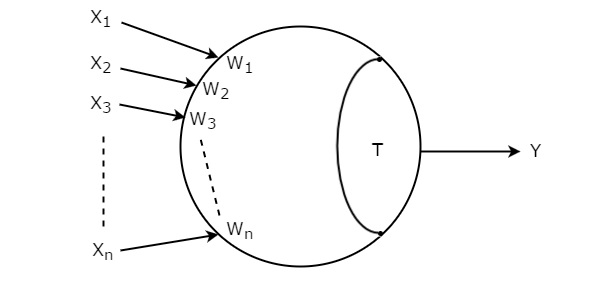
Threshold gate원으로 표시되며 'n'입력, X 1 ~ X n 및 단일 출력, Y를 갖습니다 .이 원은 두 부분으로 구성됩니다. 한 부분은 입력에 해당하는 가중치를 나타내고 다른 부분은 임계 값 T를 나타냅니다.
해당 가중치를 가진 입력의 곱의 합은 다음과 같습니다. weighted sum. 이 가중치 합이 임계 값 T보다 크거나 같으면 출력 Y 만 1과 같습니다. 그렇지 않으면 출력 Y는 0과 같습니다.
Mathematically, 우리는 Threshold gate의 입력과 출력 간의 관계를 아래와 같이 작성할 수 있습니다.
$$Y=1, if \: \: W_{1}X_{1}+W_{2}X_{2}+W_{3}X_{3}+...W_{n}X_{n}\geq T$$
= 0, 그렇지 않으면.
따라서 가중치 및 / 또는 임계 값 T의 값을 변경하여 다양한 논리 게이트와 부울 함수를 구현할 수 있습니다.
예
우리가 simplified Boolean function 다음 임계 값 게이트의 경우.

이 임계 값 게이트에는 3 개의 입력 X 1 , X 2 , X 3 및 1 개의 출력 Y가 있습니다.
입력 X 1 , X 2 및 X 3에 해당하는 가중치 는 각각 W 1 = 2, W 2 = 1 및 W 3 = -4입니다.
Threshold gate의 값은 T = -1입니다.
그만큼 weighted sum 문턱 게이트의
$$W=W_{1}X_{1}+W_{2}X_{2}+W_{3}X_{3}$$
위 방정식에서 주어진 가중치를 대체하십시오.
$$\Rightarrow W=2X_{1}+X_{2}-4X_{3}$$
임계 값 게이트의 출력, W ≥ −1이면 Y는 '1'이되고, 그렇지 않으면 '0'이됩니다.
다음과 같은 table 가능한 모든 입력 조합에 대한 입력과 출력 간의 관계를 보여줍니다.
| 입력 | 가중 합계 | 산출 | ||
|---|---|---|---|---|
| $X_{1}$ | $X_{2}$ | $X_{3}$ | $W=2X_{1}+X_{2}-4X_{3}$ | $Y$ |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | -4 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | -삼 | 0 |
| 1 | 0 | 0 | 2 | 1 |
| 1 | 0 | 1 | -2 | 0 |
| 1 | 1 | 0 | 삼 | 1 |
| 1 | 1 | 1 | -1 | 1 |
위의 표에서 우리는 Boolean function 출력의 경우 Y는
$$Y= \sum m\left ( 0,2,4,6,7 \right )$$
이 부울 함수의 단순화는 3 variable K-Map 다음 그림에 나와 있습니다.

따라서 simplified Boolean function 주어진 문턱 게이트에 대해 $Y={X_{3}'}+X_{1}X_{2}$.
임계 값 함수의 합성
임계 값 게이트는 universal gate임계 값 게이트를 사용하여 모든 부울 함수를 구현할 수 있기 때문입니다. 때로는 단일 임계 값 게이트를 사용하여 논리 게이트와 부울 함수를 거의 구현하지 못할 수도 있습니다. 이 경우 여러 임계 값 게이트가 필요할 수 있습니다.
다음을 따르십시오 steps 단일 임계 값 게이트를 사용하여 부울 함수를 구현합니다.
Step 1 − 공식화 Truth table 주어진 부울 함수에 대해.
Step 2 − 위의 Truth 테이블에서 하나 이상의 열을 추가 (포함)하여 다음과 같은 관계를 제공합니다. weighted sums 과 Threshold value.
Step 3 − 아래에 언급 된대로 각 입력 조합에 대한 가중 합계와 임계 값 간의 관계를 작성합니다.
부울 함수의 출력이 1이면 가중치 합은 해당 입력 조합에 대한 임계 값보다 크거나 같습니다.
부울 함수의 출력이 0이면 가중치 합이 해당 입력 조합에 대한 임계 값보다 작습니다.
Step 4 − 위 표의 마지막 열에있는 모든 관계를 만족하는 방식으로 가중치 및 임계 값을 선택합니다.
step 5 − 그리기 symbol 그 가중치와 임계 값을 가진 임계 값 게이트의.
예
다음을 구현하겠습니다. Boolean function 단일 임계 값 게이트를 사용합니다.
$$Y\left ( X_{1},X_{2},X_{3} \right )=\sum m\left ( 0,2,4,6,7 \right )$$
주어진 부울 함수는 최소 항의 합으로 표현되는 세 가지 변수 함수입니다. 그만큼Truth table 이 기능에 대한 설명은 다음과 같습니다.
| 입력 | 산출 | ||
|---|---|---|---|
| X1 | X2 | X3 | Y |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
이제 위의 Truth 테이블에 열을 하나 더 추가 (포함)하겠습니다. 이 마지막 열에는weighted sums (W) and Threshold 각 입력 조합에 대한 값 (T).
| 입력 | 산출 | W와 T의 관계 | ||
|---|---|---|---|---|
| X1 | X2 | X3 | Y | |
| 0 | 0 | 0 | 1 | 0 ≥T |
| 0 | 0 | 1 | 0 | 승 3 <T |
| 0 | 1 | 0 | 1 | 승 2 ≥ T |
| 0 | 1 | 1 | 0 | 승 2 + 승 3 <T |
| 1 | 0 | 0 | 1 | 승 1 ≥ T |
| 1 | 0 | 1 | 0 | 승 1 + 승 3 <T |
| 1 | 1 | 0 | 1 | 승 1 + 승 2 ≥ T |
| 1 | 1 | 1 | 1 | 승 1 + 승 2 + 승 3 ≥ T |
다음은 위 표의 결론입니다.
임계 값은 첫 번째 관계에 따라 0이거나 음수 여야합니다.
W 3 의 값은 첫 번째 및 두 번째 관계를 기반으로 음수 여야합니다.
W 1 및 W 2의 값은 다섯 번째 및 세 번째 관계를 기반으로하는 임계 값보다 크거나 같아야합니다.
네 번째 관계를 기반으로 W 2 는 W 3 보다 커야 합니다.
위의 결론을 기반으로 가중치 및 임계 값에 대해 다음 값을 선택할 수 있습니다.
승 1 = 2, 승 2 = 1, 승 3 = -4 & T = -1
그만큼 symbol 위의 값을 가진 Threshold gate의 값은 아래와 같습니다.

따라서이 임계 값 게이트는 주어진 Boolean function, $Y\left ( X_{1}, X_{2},X_{3} \right )=\sum m\left ( 0,2,4,6,7 \right )$.
이전 장에서 다양한 조합 회로에 대해 논의했습니다. 이 모든 회로에는 현재 입력 조합에만 의존하는 출력 세트가 있습니다. 다음 그림은block diagram 순차 회로의.
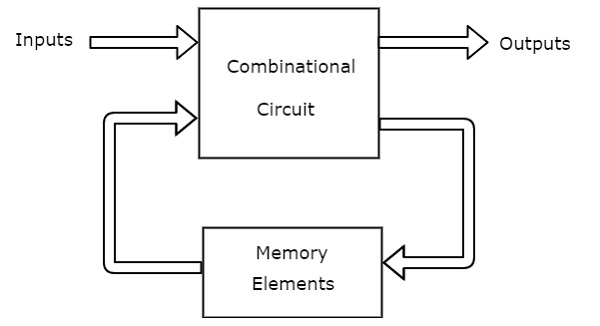
이 순차 회로에는 입력 및 출력 세트가 포함되어 있습니다. 순차 회로의 출력은 현재 입력의 조합뿐만 아니라 이전 출력에도 의존합니다. 이전 출력은present state. 따라서 순차 회로에는 메모리 (저장) 요소와 함께 조합 회로가 포함됩니다. 일부 순차 회로는 조합 회로가 아니라 메모리 요소 만 포함 할 수 있습니다.
다음 표는 differences 조합 회로와 순차 회로 사이.
| 조합 회로 | 순차 회로 |
|---|---|
| 출력은 현재 입력에만 의존합니다. | 출력은 현재 입력과 현재 상태에 따라 다릅니다. |
| 피드백 경로가 없습니다. | 피드백 경로가 있습니다. |
| 메모리 요소는 필요하지 않습니다. | 메모리 요소가 필요합니다. |
| 클록 신호는 필요하지 않습니다. | 시계 신호가 필요합니다. |
| 디자인하기 쉽습니다. | 디자인하기 어렵습니다. |
순차 회로의 유형
다음은 두 가지 유형의 순차 회로입니다.
- 비동기 순차 회로
- 동기 순차 회로
비동기 순차 회로
순차 회로의 일부 또는 모든 출력이 클록 신호의 활성 전환과 관련하여 변경 (영향)되지 않으면 해당 순차 회로를 다음과 같이 호출합니다. Asynchronous sequential circuit. 즉, 비동기 순차 회로의 모든 출력이 동시에 변경 (영향)되지 않습니다. 따라서 비동기 순차 회로의 대부분의 출력은not in synchronous 클럭 신호의 포지티브 에지 또는 네거티브 에지 만 사용합니다.
동기 순차 회로
순차 회로의 모든 출력이 클록 신호의 활성 전환과 관련하여 변경 (영향)되면 해당 순차 회로는 다음과 같이 호출됩니다. Synchronous sequential circuit. 즉, 동기 순차 회로의 모든 출력이 동시에 변경 (영향)됩니다. 따라서 동기 순차 회로의 출력은 클럭 신호의 양의 에지 또는 음의 에지와 만 동기됩니다.
클록 신호 및 트리거링
이 섹션에서는 클럭 신호와 트리거링 유형에 대해 하나씩 설명하겠습니다.
시계 신호
클럭 신호는주기적인 신호이며 ON 시간과 OFF 시간이 같을 필요는 없습니다. 클럭 신호를 다음과 같이 나타낼 수 있습니다.square wave, ON 시간과 OFF 시간이 모두 같을 때. 이 클럭 신호는 다음 그림에 나와 있습니다.

위 그림에서 구형파는 클럭 신호로 간주됩니다. 이 신호는 일정 시간 동안 로직 High (5V)에 유지되고 동일한 시간 동안 로직 Low (0V)에 유지됩니다. 이 패턴은 일정 기간 동안 반복됩니다. 이 경우time period ON 시간의 두 배 또는 OFF 시간의 두 배와 같습니다.
클럭 신호를 다음과 같이 나타낼 수 있습니다. train of pulses, ON 시간과 OFF 시간이 동일하지 않을 때. 이 클럭 신호는 다음 그림에 나와 있습니다.

위 그림에서 펄스열은 클럭 신호로 간주됩니다. 이 신호는 일정 시간 동안 로직 하이 (5V)로 유지되고 다른 시간 동안 로직 로우 (0V)로 유지됩니다. 이 패턴은 일정 기간 동안 반복됩니다. 이 경우time period ON 시간과 OFF 시간의 합과 같습니다.
클럭 신호의 시간주기의 역수는 frequency클록 신호의. 모든 순차 회로는 클럭 신호로 작동합니다. 따라서 순차적 회로가 작동 될 수있는 주파수는 클럭 신호 주파수를 선택해야합니다.
트리거링 유형
다음은 순차 회로에서 사용되는 두 가지 가능한 트리거링 유형입니다.
- 레벨 트리거
- 에지 트리거링
레벨 트리거
클럭 신호에는 로직 High와 로직 Low의 두 가지 레벨이 있습니다. 다음은 두 가지입니다.types of level triggering.
- 포지티브 레벨 트리거
- 네거티브 레벨 트리거링
순차 회로가 클럭 신호로 동작하는 경우 Logic High이면 해당 유형의 트리거를 Positive level triggering. 아래 그림에서 강조 표시됩니다.
순차 회로가 클럭 신호로 동작하는 경우 Logic Low이면 해당 유형의 트리거를 Negative level triggering. 다음 그림에서 강조 표시됩니다.

에지 트리거링
클록 신호에서 발생하는 두 가지 유형의 전환이 있습니다. 즉, 클록 신호가 Logic Low에서 Logic High로 또는 Logic High에서 Logic Low로 전환됩니다.
다음은 두 가지입니다. types of edge triggering 클럭 신호의 전환을 기반으로합니다.
- 포지티브 에지 트리거링
- 네거티브 에지 트리거링
순차 회로가 Logic Low에서 Logic High로 전환되는 클록 신호로 작동되는 경우 해당 유형의 트리거링은 Positive edge triggering. 상승 에지 트리거링이라고도합니다. 다음 그림에 나와 있습니다.

순차 회로가 Logic High에서 Logic Low로 전환되는 클럭 신호로 작동되는 경우 해당 유형의 트리거링은 Negative edge triggering. 하강 에지 트리거링이라고도합니다. 다음 그림에 나와 있습니다.

다음 장에서는 사용할 수있는 트리거링 유형에 따라 다양한 순차 회로에 대해 설명합니다.
작동에 적합한 트리거링 유형에 따라 두 가지 유형의 메모리 요소가 있습니다.
- Latches
- Flip-flops
래치는 활성화 신호로 작동합니다. level sensitive. 반면 플립 플롭은 가장자리에 민감합니다. 다음 장에서 플립 플롭에 대해 논의 할 것입니다. 이제 SR Latch와 D Latch에 대해 하나씩 살펴 보겠습니다.
SR 래치
SR 래치는 Set Reset Latch. 이 래치는 활성화 E가 '1'로 유지되는 한 출력에 영향을 미칩니다. 그만큼circuit diagram SR Latch의 구성은 다음 그림과 같습니다.
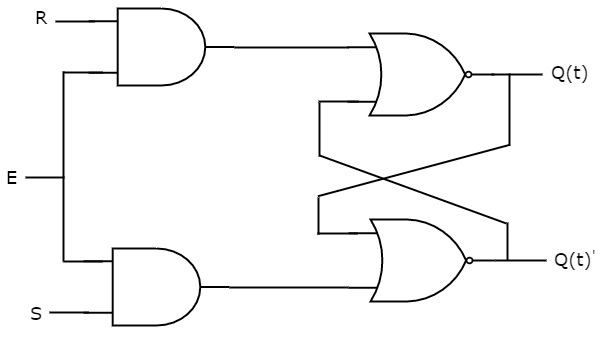
이 회로에는 두 개의 입력 S 및 R과 두 개의 출력 Q (t) 및 Q (t) '가 있습니다. 그만큼upper NOR gate 두 개의 입력 R & 현재 상태의 보완 인 Q (t) '를 가지며 다음 상태 인 Q (t + 1)을 생성합니다. 활성화되면 E는'1 '입니다.
마찬가지로 lower NOR gate 두 개의 입력 S & 현재 상태, Q (t)를 가지며 활성화되면 다음 상태 Q (t + 1) '의 보완을 생성하고 E는'1 '입니다.
우리는 2-input NOR gate입력 중 하나가 '0'일 때 다른 입력을 보완하는 출력을 생성합니다. 마찬가지로 입력 중 하나가 '1'이면 '0'출력을 생성합니다.
S = 1이면 다음 상태 Q (t + 1)는 현재 상태, Q (t) 값에 관계없이 '1'과 같습니다.
R = 1이면 다음 상태 Q (t + 1)는 현재 상태, Q (t) 값에 관계없이 '0'과 같습니다.
언제든지이 두 입력 중 '1'만 있어야합니다. 두 입력이 모두 '1'이면 다음 상태 Q (t + 1) 값이 정의되지 않습니다.
다음 표는 state table SR 래치의.
| 에스 | 아르 자형 | Q (t + 1) |
|---|---|---|
| 0 | 0 | Q (t) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | - |
따라서 SR Latch는 입력 조건에 따라 Hold, Set, Reset의 3 가지 기능을 수행합니다.
D 래치
SR 래치에는 한 가지 단점이 있습니다. 그것은 입력 S와 R이 모두 하나 일 때 다음 상태 값을 예측할 수 없습니다. 그래서 우리는 D Latch로이 어려움을 극복 할 수 있습니다. 데이터 래치라고도합니다. 그만큼circuit diagram D Latch의 그림은 다음과 같습니다.

이 회로에는 단일 입력 D와 두 개의 출력 Q (t) 및 Q (t) '가 있습니다. D Latch는 S amp; & R 입력 사이에 인버터를 배치하고 D 입력을 S에 연결하여 SR Latch에서 얻습니다. 즉, S와 R의 조합이 동일한 값을 갖는 것을 제거했습니다.
D = 0 → S = 0 & R = 1이면 다음 상태 Q (t + 1)는 현재 상태, Q (t) 값에 관계없이 '0'과 같습니다. 이것은 SR Latch 상태 테이블의 두 번째 행에 해당합니다.
D = 1 → S = 1 & R = 0이면 다음 상태 Q (t + 1)는 현재 상태, Q (t) 값에 관계없이 '1'과 같습니다. 이것은 SR Latch 상태 테이블의 세 번째 행에 해당합니다.
다음 표는 state table D 래치의.
| 디 | Q (t + 1) |
|---|---|
| 0 | 0 |
| 1 | 1 |
따라서 D Latch는 데이터 입력 D에서 사용할 수있는 정보를 유지합니다. 이는 D Latch의 출력이 인 에이블이 High 인 한 입력의 변경에 민감하다는 것을 의미합니다.
이 장에서는 NOR 게이트 간의 교차 결합을 제공하여 다양한 래치를 구현했습니다. 마찬가지로 NAND 게이트를 사용하여 이러한 래치를 구현할 수 있습니다.
이전 장에서 래치에 대해 논의했습니다. 그것들은 플립 플롭의 기본 구성 요소입니다. 두 가지 방법으로 플립 플롭을 구현할 수 있습니다.
첫 번째 방법에서는 cascade two latches이러한 방식으로 첫 번째 래치는 모든 양의 클록 펄스에 대해 활성화되고 두 번째 래치는 모든 음의 클록 펄스에 대해 활성화됩니다. 이 두 래치의 조합이 플립 플롭이되도록합니다.
두 번째 방법에서는 에지에 민감한 플립 플롭을 직접 구현할 수 있습니다. 이 장에서는 다음 사항에 대해 논의하겠습니다.flip-flops 두 번째 방법을 사용합니다.
- SR 플립 플롭
- D 플립 플롭
- JK 플립 플롭
- T 플립 플롭
SR 플립 플롭
SR 플립 플롭은 양의 클럭 전환 또는 음의 클럭 전환으로 만 작동합니다. 반면 SR 래치는 활성화 신호로 작동합니다. 그만큼circuit diagram SR 플립 플롭의 특성은 다음 그림과 같습니다.

이 회로에는 두 개의 입력 S 및 R과 두 개의 출력 Q (t) 및 Q (t) '가 있습니다. SR flipflop의 작동은 SR Latch와 유사합니다. 그러나이 플립 플롭은 액티브 인 에이블 대신 클록 신호의 포지티브 전환이 적용될 때만 출력에 영향을 미칩니다.
다음 표는 state table SR 플립 플롭의.
| 에스 | 아르 자형 | Q (t + 1) |
|---|---|---|
| 0 | 0 | Q (t) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | - |
여기서 Q (t) & Q (t + 1)은 각각 현재 상태와 다음 상태입니다. 따라서 SR 플립 플롭은 클럭 신호의 포지티브 전환이 적용될 때 입력 조건에 따라 Hold, Reset 및 Set과 같은 세 가지 기능 중 하나에 사용할 수 있습니다. 다음 표는characteristic table SR 플립 플롭의.
| 현재 입력 | 현재 상태 | 다음 상태 | |
|---|---|---|---|
| S | R | Q(t) | Q(t + 1) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 엑스 |
| 1 | 1 | 1 | 엑스 |
세 개의 변수 K-Map을 사용하면 다음 상태 Q (t + 1)에 대한 단순화 된 표현을 얻을 수 있습니다. 그만큼three variable K-Map 다음 상태의 경우 Q (t + 1)가 다음 그림에 표시됩니다.

인접한 그룹의 최대 가능한 그룹이 이미 그림에 표시되어 있습니다. 따라서simplified expression 다음 상태 Q (t + 1)에 대해
$Q\left ( t+1 \right )=S+{R}'Q\left ( t \right )$
D 플립 플롭
D 플립 플롭은 양의 클록 전환 또는 음의 클록 전환으로 만 작동합니다. 반면 D 래치는 활성화 신호로 작동합니다. 즉, D 플립 플롭의 출력은 클럭 신호의 활성 전환을 제외하고 입력 D의 변화에 민감하지 않습니다. 그만큼circuit diagram D 플립 플롭의 다음 그림에 나와 있습니다.

이 회로에는 단일 입력 D와 두 개의 출력 Q (t) 및 Q (t) '가 있습니다. D 플립 플롭의 작동은 D 래치와 유사합니다. 그러나이 플립 플롭은 액티브 인 에이블 대신 클록 신호의 포지티브 전환이 적용될 때만 출력에 영향을 미칩니다.
다음 표는 state table D 플립 플롭의.
| 디 | Qt + 1t + 1 |
|---|---|
| 0 | 0 |
| 1 | 1 |
따라서 D 플립 플롭은 항상 데이터 입력에서 사용할 수있는 정보를 유지합니다. D는 클럭 신호의 이전 포지티브 전환입니다. 위의 상태 테이블에서 다음 상태 방정식을 다음과 같이 직접 작성할 수 있습니다.
Q (t + 1) = D
D 플립 플롭의 다음 상태는 클럭 신호의 모든 양의 전환에 대해 항상 데이터 입력 D와 동일합니다. 따라서 D 플립 플롭은 레지스터에서 사용할 수 있습니다.shift registers 및 일부 카운터.
JK 플립 플롭
JK 플립 플롭은 SR 플립 플롭의 수정 된 버전입니다. 양의 클럭 전환 또는 음의 클럭 전환으로 만 작동합니다. 그만큼circuit diagram JK 플립 플롭의 내용은 다음 그림과 같습니다.
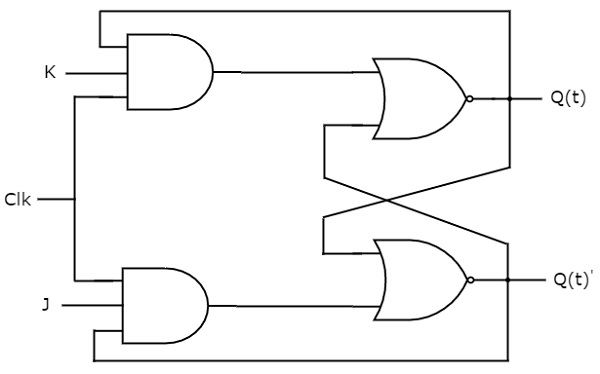
이 회로에는 두 개의 입력 J 및 K와 두 개의 출력 Q (t) 및 Q (t) '가 있습니다. JK 플립 플롭의 작동은 SR 플립 플롭과 유사합니다. 여기서 우리는 SR 플립 플롭의 입력을 다음과 같이 고려했습니다.S = J Q(t)’ 과 R = KQ(t) 4 개의 입력 조합에 대해 수정 된 SR 플립 플롭을 활용하기 위해.
다음 표는 state table JK 플립 플롭의.
| 제이 | 케이 | Q (t + 1) |
|---|---|---|
| 0 | 0 | Q (t) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | Q (t) ' |
여기서 Q (t) & Q (t + 1)은 각각 현재 상태와 다음 상태입니다. 따라서 JK 플립 플롭은 클럭 신호의 포지티브 전환이 적용될 때 입력 조건에 따라 현재 상태의 Hold, Reset, Set 및 Complement와 같은 4 가지 기능 중 하나에 사용할 수 있습니다. 다음 표는characteristic table JK 플립 플롭의.
| 현재 입력 | 현재 상태 | 다음 상태 | |
|---|---|---|---|
| J | K | Q(t) | Q(t+1) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
세 개의 변수 K-Map을 사용하면 다음 상태 Q (t + 1)에 대한 단순화 된 표현을 얻을 수 있습니다. Three variable K-Map 다음 상태의 경우 Q (t + 1)가 다음 그림에 표시됩니다.

인접한 그룹의 최대 가능한 그룹이 이미 그림에 표시되어 있습니다. 따라서simplified expression 다음 상태 Q (t + 1)는
$$Q\left ( t+1 \right )=J{Q\left ( t \right )}'+{K}'Q\left ( t \right )$$
T 플립 플롭
T 플립 플롭은 JK 플립 플롭의 단순화 된 버전입니다. 동일한 입력 'T'를 JK 플립 플롭의 두 입력에 연결하여 얻습니다. 양의 클럭 전환 또는 음의 클럭 전환으로 만 작동합니다. 그만큼circuit diagram T 플립 플롭의 다음 그림에 나와 있습니다.

이 회로에는 단일 입력 T와 두 개의 출력 Q (t) 및 Q (t) '가 있습니다. T 플립 플롭의 동작은 JK 플립 플롭의 동작과 동일합니다. 여기서 우리는 JK 플립 플롭의 입력을 다음과 같이 고려했습니다.J = T 과 K = T2 개의 입력 조합에 대해 수정 된 JK 플립 플롭을 활용하기 위해. 그래서 우리는 J와 K의 다른 두 조합을 제거했습니다.이 두 값은 T 플립 플롭에서 서로 보완됩니다.
다음 표는 state table T 플립 플롭의.
| 디 | Q (t + 1) |
|---|---|
| 0 | Q (t) |
| 1 | Q (t) ' |
여기서 Q (t) & Q (t + 1)은 각각 현재 상태와 다음 상태입니다. 따라서 T 플립 플롭은 클럭 신호의 양의 천이가 적용될 때 입력 조건에 따라 Hold, 현재 상태의 보완과 같은 두 가지 기능 중 하나에 사용할 수 있습니다. 다음 표는characteristic table T 플립 플롭의.
| 입력 | 현재 상태 | 다음 상태 |
|---|---|---|
| T | Q(t) | Q(t + 1) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
위의 특성 표에서 직접 작성할 수 있습니다. next state equation 같이
$$Q\left ( t+1 \right )={T}'Q\left ( t \right )+TQ{\left ( t \right )}'$$
$$\Rightarrow Q\left ( t+1 \right )=T\oplus Q\left ( t \right )$$
T 플립 플롭의 출력은 입력 T가 로직 하이 (1)로 유지 될 때 클록 신호의 모든 양의 전환에 대해 항상 토글됩니다. 따라서 T 플립 플롭은counters.
이 장에서는 NOR 게이트 간의 교차 결합을 제공하여 다양한 플립 플롭을 구현했습니다. 마찬가지로 NAND 게이트를 사용하여 이러한 플립 플롭을 구현할 수 있습니다.
이전 장에서 우리는 SR 플립 플롭, D 플립 플롭, JK 플립 플롭 및 T 플립 플롭의 네 가지 플립 플롭에 대해 논의했습니다. 추가 로직을 포함하여 하나의 플립 플롭을 나머지 3 개의 플립 플롭으로 변환 할 수 있습니다. 그래서 총 12 개의flip-flop conversions.
다음을 따르십시오 steps 하나의 플립 플롭을 다른 플립 플롭으로 변환합니다.
고려하다 characteristic table 원하는 플립 플롭의.
현재 상태와 다음 상태의 각 조합에 대해 주어진 플립 플롭의 여기 값 (입력)을 채 웁니다. 그만큼excitation table 모든 플립 플롭의 경우 아래에 나와 있습니다.
| 현재 상태 | 다음 상태 | SR 플립 플롭 입력 | D 플립 플롭 입력 | JK 플립 플롭 입력 | T 플립 플롭 입력 | ||
|---|---|---|---|---|---|---|---|
| Q(t) | Q(t+1) | S | R | D | J | K | T |
| 0 | 0 | 0 | 엑스 | 0 | 0 | 엑스 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 | 엑스 | 1 |
| 1 | 0 | 0 | 1 | 0 | 엑스 | 1 | 1 |
| 1 | 1 | 엑스 | 0 | 1 | 엑스 | 0 | 0 |
얻기 simplified expressions각 여기 입력에 대해. 필요한 경우 단순화를 위해 Kmaps를 사용하십시오.
그리기 circuit diagram 주어진 플립 플롭과 필요한 논리 게이트를 사용하여 단순화 된 표현에 따라 원하는 플립 플롭의.
이제 몇 개의 플립 플롭을 다른 것으로 변환 해 보겠습니다. 나머지 플립 플롭 변환에 대해 동일한 프로세스를 따르십시오.
SR Flip-Flop에서 다른 Flip-Flop으로 변환
다음은 SR 플립 플롭에서 다른 플립 플롭으로의 세 가지 가능한 변환입니다.
- SR 플립 플롭에서 D 플립 플롭으로
- SR 플립 플롭에서 JK 플립 플롭으로
- SR 플립 플롭에서 T 플립 플롭으로
SR 플립 플롭에서 D 플립 플롭으로 변환
여기서 주어진 플립 플롭은 SR 플립 플롭이고 원하는 플립 플롭은 D 플립 플롭입니다. 따라서 다음을 고려하십시오.characteristic table D 플립 플롭의.
| D 플립 플롭 입력 | 현재 상태 | 다음 상태 |
|---|---|---|
| D | Q(t) | Q(t + 1) |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
우리는 SR 플립 플롭에 두 개의 입력 S & R이 있다는 것을 알고 있습니다. 따라서 현재 상태와 다음 상태 값의 각 조합에 대한 SR 플립 플롭의 여기 값을 기록하십시오. 다음 표는 D 플립 플롭의 특성 테이블과 함께excitation inputs SR 플립 플롭의.
| D 플립 플롭 입력 | 현재 상태 | 다음 상태 | SR 플립 플롭 입력 | |
|---|---|---|---|---|
| D | Q(t) | Q(t + 1) | S | R |
| 0 | 0 | 0 | 0 | 엑스 |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 엑스 | 0 |
위의 표에서 우리는 Boolean functions 각 입력에 대해 아래와 같이.
$$S=m_{2}+d_{3}$$
$$R=m_{1}+d_{0}$$
이러한 입력에 대한 단순화 된 표현을 얻기 위해 2 개의 변수 K- 맵을 사용할 수 있습니다. 그만큼k-Maps S & R의 경우는 아래와 같습니다.

그래서 우리는 단순화 후 S = D & R = D '를 얻었습니다. 그만큼circuit diagram D 플립 플롭의 다음 그림에 나와 있습니다.

이 회로는 SR 플립 플롭과 인버터로 구성됩니다. 이 인버터는 입력 D를 보완하는 출력을 생성합니다. 따라서 전체 회로에는 단일 입력 D와 두 개의 출력 Q (t) & Q (t) '가 있습니다. 따라서D flip-flop. 마찬가지로 다른 두 가지 변환을 수행 할 수 있습니다.
D Flip-Flop에서 다른 Flip-Flop으로 변환
다음은 D 플립 플롭에서 다른 플립 플롭으로의 세 가지 가능한 변환입니다.
- D 플립 플롭에서 T 플립 플롭으로
- D 플립 플롭에서 SR 플립 플롭으로
- D 플립 플롭에서 JK 플립 플롭으로
D 플립 플롭에서 T 플립 플롭으로 변환
여기서 주어진 플립 플롭은 D 플립 플롭이고 원하는 플립 플롭은 T 플립 플롭입니다. 따라서 다음을 고려하십시오.characteristic table T 플립 플롭의.
| T 플립 플롭 입력 | 현재 상태 | 다음 상태 |
|---|---|---|
| T | Q(t) | Q(t + 1) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
우리는 D 플립 플롭에 단일 입력 D가 있다는 것을 알고 있습니다. 따라서 현재 상태와 다음 상태 값의 각 조합에 대해 D 플립 플롭의 여기 값을 기록하십시오. 다음 표는 T 플립 플롭의 특성 테이블과 함께excitation input D 플립 플롭의.
| T 플립 플롭 입력 | 현재 상태 | 다음 상태 | D 플립 플롭 입력 |
|---|---|---|---|
| T | Q(t) | Q(t + 1) | D |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
위의 표에서 직접 작성할 수 있습니다. Boolean function D의 다음과 같이.
$$D=T\oplus Q\left ( t \right )$$
따라서 D 플립 플롭과 함께 두 개의 입력 Exclusive-OR 게이트가 필요합니다. 그만큼circuit diagram T 플립 플롭의 다음 그림에 나와 있습니다.

이 회로는 D 플립 플롭과 Exclusive-OR 게이트로 구성됩니다. 이 Exclusive-OR 게이트는 T와 Q (t)의 Ex-OR 인 출력을 생성합니다. 따라서 전체 회로에는 단일 입력, T 및 두 개의 출력 Q (t) 및 Q (t) '가 있습니다. 따라서T flip-flop. 마찬가지로 다른 두 가지 변환을 수행 할 수 있습니다.
JK Flip-Flop에서 다른 Flip-Flop으로 변환
다음은 JK 플립 플롭에서 다른 플립 플롭으로의 가능한 세 가지 변환입니다.
- JK 플립 플롭에서 T 플립 플롭으로
- JK 플립 플롭에서 D 플립 플롭으로
- JK 플립 플롭에서 SR 플립 플롭으로
JK 플립 플롭에서 T 플립 플롭으로 변환
여기서 주어진 플립 플롭은 JK 플립 플롭이고 원하는 플립 플롭은 T 플립 플롭입니다. 따라서 다음을 고려하십시오.characteristic table T 플립 플롭의.
| T 플립 플롭 입력 | 현재 상태 | 다음 상태 |
|---|---|---|
| T | Q(t) | Q(t + 1) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
JK 플립 플롭에는 두 개의 입력 J & K가 있다는 것을 알고 있습니다. 따라서 현재 상태 값과 다음 상태 값의 각 조합에 대해 JK 플립 플롭의 여기 값을 기록하십시오. 다음 표는 T 플립 플롭의 특성 테이블과 함께excitation inputs JK 플립 플롭의.
| T 플립 플롭 입력 | 현재 상태 | 다음 상태 | JK 플립 플롭 입력 | |
|---|---|---|---|---|
| T | Q(t) | Q(t + 1) | J | K |
| 0 | 0 | 0 | 0 | 엑스 |
| 0 | 1 | 1 | 엑스 | 0 |
| 1 | 0 | 1 | 1 | 엑스 |
| 1 | 1 | 0 | 엑스 | 1 |
위의 표에서 우리는 Boolean functions 각 입력에 대해 아래와 같이.
$$J=m_{2}+d_{1}+d_{3}$$
$$K=m_{3}+d_{0}+d_{2}$$
이 두 입력에 대해 단순화 된 표현식을 얻기 위해 2 개의 변수 K-Map을 사용할 수 있습니다. 그만큼k-Maps J & K의 경우는 아래와 같습니다.

그래서 우리는 단순화 후 J = T & K = T를 얻었습니다. 그만큼circuit diagram T 플립 플롭의 다음 그림에 나와 있습니다.

이 회로는 JK 플립 플롭으로 만 구성됩니다. 다른 게이트가 필요하지 않습니다. 동일한 입력 T를 J와 K 모두에 연결하기 만하면됩니다. 따라서 전체 회로에는 단일 입력, T 및 두 개의 출력 Q (t) 및 Q (t) '가 있습니다. 따라서T flip-flop. 마찬가지로 다른 두 가지 변환을 수행 할 수 있습니다.
T Flip-Flop에서 다른 Flip-Flop으로 변환
다음은 T 플립 플롭에서 다른 플립 플롭으로의 세 가지 가능한 변환입니다.
- T 플립 플롭에서 D 플립 플롭으로
- T 플립 플롭에서 SR 플립 플롭으로
- T 플립 플롭에서 JK 플립 플롭으로
T 플립 플롭에서 D 플립 플롭으로 변환
여기서 주어진 플립 플롭은 T 플립 플롭이고 원하는 플립 플롭은 D 플립 플롭입니다. 따라서 D 플립 플롭의 특성 표를 고려하고 현재 상태 값과 다음 상태 값의 각 조합에 대한 T 플립 플롭의 여기 값을 기록하십시오. 다음 표는characteristic table D 플립 플롭의 excitation input T 플립 플롭의.
| D 플립 플롭 입력 | 현재 상태 | 다음 상태 | T 플립 플롭 입력 | |
|---|---|---|---|---|
| D | Q(t) | Q(t + 1) | T | |
| 0 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 1 | |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 1 | 0 | |
위의 표에서 아래와 같이 T의 Boolean 함수를 직접 작성할 수 있습니다.
$$T=D\oplus Q\left ( t \right )$$
따라서 T 플립 플롭과 함께 2 개의 입력 Exclusive-OR 게이트가 필요합니다. 그만큼circuit diagram D 플립 플롭의 다음 그림에 나와 있습니다.

이 회로는 T 플립 플롭과 Exclusive-OR 게이트로 구성됩니다. 이 Exclusive-OR 게이트는 D와 Q (t)의 Ex-OR 인 출력을 생성합니다. 따라서 전체 회로에는 단일 입력, D 및 두 개의 출력 Q (t) 및 Q (t) '가 있습니다. 따라서D flip-flop. 마찬가지로 다른 두 가지 변환을 수행 할 수 있습니다.
우리는 하나의 플립 플롭이 1 비트의 정보를 저장할 수 있다는 것을 알고 있습니다. 여러 비트의 정보를 저장하려면 여러 개의 플립 플롭이 필요합니다. 바이너리 데이터를 보관 (저장)하는 데 사용되는 플립 플롭 그룹은 다음과 같이 알려져 있습니다.register.
레지스터가 비트를 오른쪽 또는 왼쪽으로 이동할 수있는 경우 shift register. 'N'비트 시프트 레지스터에는 'N'플립 플롭이 포함됩니다. 다음은 입력 적용 및 출력 액세스를 기반으로하는 네 가지 유형의 시프트 레지스터입니다.
- 직렬 입력-직렬 출력 시프트 레지스터
- 직렬 입력-병렬 출력 시프트 레지스터
- Parallel In − Serial Out 시프트 레지스터
- Parallel In − Parallel Out 시프트 레지스터
직렬 입력-직렬 출력 (SISO) 시프트 레지스터
직렬 입력을 허용하고 직렬 출력을 생성하는 시프트 레지스터는 직렬 입력 – 직렬 출력으로 알려져 있습니다. (SISO)시프트 레지스터. 그만큼block diagram 3 비트 SISO 시프트 레지스터의 그림은 다음과 같습니다.

이 블록 다이어그램은 3 개의 D 플립 플롭으로 구성됩니다. cascaded. 즉, 하나의 D 플립 플롭의 출력이 다음 D 플립 플롭의 입력으로 연결됩니다. 이러한 모든 플립 플롭은 동일한 클럭 신호가 각각에 적용되기 때문에 서로 동기화됩니다.
이 시프트 레지스터에서 우리는 가장 왼쪽 D 플립 플롭의 입력에서 직렬로 비트를 보낼 수 있습니다. 따라서이 입력은 다음과 같이 호출됩니다.serial input. 클록 신호의 모든 포지티브 에지 트리거링에 대해 데이터는 한 단계에서 다음 단계로 이동합니다. 따라서 우리는 대부분의 D 플립 플롭의 출력에서 직렬로 비트를 수신 할 수 있습니다. 따라서이 출력은 다음과 같이 호출됩니다.serial output.
예
바이너리 정보를 전송하여 3 비트 SISO 시프트 레지스터의 작동을 살펴 보겠습니다. “011” 입력에서 직렬로 LSB에서 MSB로.
가장 왼쪽에서 가장 오른쪽으로 D 플립 플롭의 초기 상태는 $Q_{2}Q_{1}Q_{0}=000$. 우리는 이해할 수 있습니다working of 3-bit SISO shift register 다음 표에서.
| 클록의 양의 에지 없음 | 직렬 입력 | 질문 2 | 질문 1 | 질문 0 |
|---|---|---|---|---|
| 0 | - | 0 | 0 | 0 |
| 1 | 1 (LSB) | 1 | 0 | 0 |
| 2 | 1 | 1 | 1 | 0 |
| 삼 | 0 (MSB) | 0 | 1 | 1 (LSB) |
| 4 | - | - | 0 | 1 |
| 5 | - | - | - | 0 (MSB) |
클록 신호가 없을 때 D 플립 플롭의 초기 상태는 다음과 같습니다. $Q_{2}Q_{1}Q_{0}=000$. 여기서 직렬 출력은$Q_{0}$. 따라서 LSB (1)는 클럭의 3 번째 양의 에지 에서 수신되고 MSB (0)는 클럭의 5 번째 양의 에지 에서 수신됩니다 .
따라서 3 비트 SISO 시프트 레지스터는 유효한 출력을 생성하기 위해 5 개의 클록 펄스가 필요합니다. 마찬가지로N-bit SISO shift register 필요 2N-1 'N'비트 정보를 이동하기 위해 클럭 펄스.
직렬 입력-병렬 출력 (SIPO) 시프트 레지스터
직렬 입력을 허용하고 병렬 출력을 생성하는 시프트 레지스터는 직렬 입력 – 병렬 출력으로 알려져 있습니다. (SIPO)시프트 레지스터. 그만큼block diagram 3 비트 SIPO 시프트 레지스터의 그림은 다음과 같습니다.
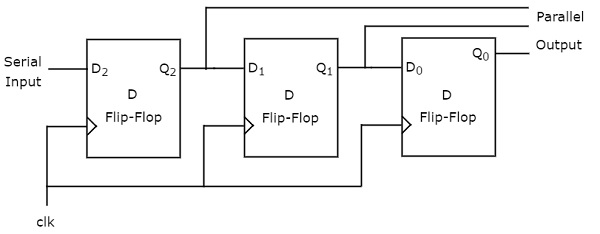
이 회로는 계단식으로 연결된 3 개의 D 플립 플롭으로 구성됩니다. 즉, 하나의 D 플립 플롭의 출력이 다음 D 플립 플롭의 입력으로 연결됩니다. 이러한 모든 플립 플롭은 동일한 클럭 신호가 각각에 적용되기 때문에 서로 동기화됩니다.
이 시프트 레지스터에서 우리는 가장 왼쪽 D 플립 플롭의 입력에서 직렬로 비트를 보낼 수 있습니다. 따라서이 입력은 다음과 같이 호출됩니다.serial input. 클록 신호의 모든 포지티브 에지 트리거링에 대해 데이터는 한 단계에서 다음 단계로 이동합니다. 이 경우 각 D 플립 플롭의 출력에 병렬로 액세스 할 수 있습니다. 그래서 우리는 얻을 것입니다parallel outputs 이 시프트 레지스터에서.
예
바이너리 정보를 전송하여 3 비트 SIPO 시프트 레지스터의 작동을 살펴 보겠습니다. “011” 입력에서 직렬로 LSB에서 MSB로.
가장 왼쪽에서 가장 오른쪽으로 D 플립 플롭의 초기 상태는 $Q_{2}Q_{1}Q_{0}=000$. 여기,$Q_{2}$ & $Q_{0}$각각 MSB 및 LSB입니다. 우리는 이해할 수 있습니다working of 3-bit SIPO shift register 다음 표에서.
| 클록의 양의 에지 없음 | 직렬 입력 | Q 2 (MSB) | 질문 1 | Q 0 (LSB) |
|---|---|---|---|---|
| 0 | - | 0 | 0 | 0 |
| 1 | 1 (LSB) | 1 | 0 | 0 |
| 2 | 1 | 1 | 1 | 0 |
| 삼 | 0 (MSB) | 0 | 1 | 1 |
클록 신호가 없을 때 D 플립 플롭의 초기 상태는 다음과 같습니다. $Q_{2}Q_{1}Q_{0}=000$. 바이너리 정보“011” 클록의 세 번째 양의 에지에 대해 D 플립 플롭의 출력에서 병렬로 획득됩니다.
따라서 3 비트 SIPO 시프트 레지스터는 유효한 출력을 생성하기 위해 3 개의 클록 펄스가 필요합니다. 마찬가지로N-bit SIPO shift register 필요 N 'N'비트 정보를 이동하기 위해 클럭 펄스.
병렬 입력-직렬 출력 (PISO) 시프트 레지스터
병렬 입력을 허용하고 직렬 출력을 생성하는 시프트 레지스터는 Parallel In-Serial Out으로 알려져 있습니다. (PISO)시프트 레지스터. 그만큼block diagram 3 비트 PISO 시프트 레지스터의 그림은 다음과 같습니다.

이 회로는 계단식으로 연결된 3 개의 D 플립 플롭으로 구성됩니다. 즉, 하나의 D 플립 플롭의 출력이 다음 D 플립 플롭의 입력으로 연결됩니다. 이러한 모든 플립 플롭은 동일한 클럭 신호가 각각에 적용되기 때문에 서로 동기화됩니다.
이 시프트 레지스터에서 우리는 parallel inputsPreset Enable을 1로 설정하여 각 D 플립 플롭으로 전환합니다. 클럭 신호의 모든 포지티브 에지 트리거에 대해 데이터는 한 단계에서 다음 단계로 이동합니다. 그래서 우리는serial output 가장 오른쪽의 D 플립 플롭에서.
예
바이너리 정보를 적용하여 3 비트 PISO 시프트 레지스터의 작동을 살펴 보겠습니다. “011” 사전 설정 입력을 통해 병렬로.
미리 설정된 입력은 Clock의 양의 에지 이전에 적용되므로 D 플립 플롭의 초기 상태는 맨 왼쪽에서 맨 오른쪽으로 $Q_{2}Q_{1}Q_{0}=011$. 우리는 이해할 수 있습니다working of 3-bit PISO shift register 다음 표에서.
| 클록의 양의 에지 없음 | 질문 2 | 질문 1 | 질문 0 |
|---|---|---|---|
| 0 | 0 | 1 | 1 (LSB) |
| 1 | - | 0 | 1 |
| 2 | - | - | 0 (LSB) |
여기서 직렬 출력은 $Q_{0}$. 따라서 LSB (1)는 클록의 양의 에지를 적용하기 전에 수신되고 MSB (0)는 클록의 두 번째 양의 에지 에서 수신됩니다 .
따라서 3 비트 PISO 시프트 레지스터는 유효한 출력을 생성하기 위해 두 개의 클록 펄스가 필요합니다. 마찬가지로N-bit PISO shift register 필요 N-1 'N'비트 정보를 이동하기 위해 클럭 펄스.
병렬 입력-병렬 출력 (PIPO) 시프트 레지스터
병렬 입력을 허용하고 병렬 출력을 생성하는 시프트 레지스터는 Parallel In-Parallel Out으로 알려져 있습니다. (PIPO)시프트 레지스터. 그만큼block diagram 3 비트 PIPO 시프트 레지스터의 그림은 다음과 같습니다.

이 회로는 계단식으로 연결된 3 개의 D 플립 플롭으로 구성됩니다. 즉, 하나의 D 플립 플롭의 출력이 다음 D 플립 플롭의 입력으로 연결됩니다. 이러한 모든 플립 플롭은 동일한 클럭 신호가 각각에 적용되기 때문에 서로 동기화됩니다.
이 시프트 레지스터에서 우리는 parallel inputsPreset Enable을 1로 설정하여 각 D 플립 플롭에 병렬 입력을 적용 할 수 있습니다. 이 두 가지는 비동기 입력입니다. 즉, 플립 플롭은 비동기 입력 값을 기반으로 해당 출력을 생성합니다. 이 경우 출력 효과는 클럭 전환과 무관합니다. 그래서 우리는parallel outputs 각 D 플립 플롭에서.
예
이진 정보를 적용하여 3 비트 PIPO 시프트 레지스터의 작동을 살펴 보겠습니다. “011” 사전 설정 입력을 통해 병렬로.
미리 설정된 입력은 Clock의 양의 에지 이전에 적용되므로 D 플립 플롭의 초기 상태는 맨 왼쪽에서 맨 오른쪽으로 $Q_{2}Q_{1}Q_{0}=011$. 그래서 바이너리 정보“011” 클럭의 양의 에지를 적용하기 전에 D 플립 플롭의 출력에서 병렬로 획득됩니다.
따라서 3 비트 PIPO 시프트 레지스터는 유효한 출력을 생성하기 위해 제로 클럭 펄스를 필요로합니다. 마찬가지로N-bit PIPO shift register 'N'비트 정보를 이동하기 위해 클록 펄스가 필요하지 않습니다.
이전 장에서 우리는 네 가지 유형의 시프트 레지스터에 대해 논의했습니다. 요구 사항에 따라 이러한 시프트 레지스터 중 하나를 사용할 수 있습니다. 다음은 시프트 레지스터의 응용입니다.
시프트 레지스터는 다음과 같이 사용됩니다. Parallel to serial converter, 병렬 데이터를 직렬 데이터로 변환합니다. ADC (Analog to Digital Converter) 블록 뒤의 송신기 섹션에서 사용됩니다.
시프트 레지스터는 다음과 같이 사용됩니다. Serial to parallel converter, 직렬 데이터를 병렬 데이터로 변환합니다. DAC (Digital to Analog Converter) 블록 이전의 수신기 섹션에서 사용됩니다.
일부 추가 게이트와 함께 시프트 레지스터는 0과 1의 시퀀스를 생성합니다. 따라서 다음과 같이 사용됩니다.sequence generator.
시프트 레지스터는 다음과 같이 사용됩니다. counters. 대부분의 D 플립 플롭이 직렬 입력에 연결된 출력 유형에 따라 두 가지 유형의 카운터가 있습니다. 링 카운터와 존슨 링 카운터입니다.
이 장에서는이 두 카운터에 대해 하나씩 설명하겠습니다.
링 카운터
이전 장에서 직렬 입력-병렬 출력의 작동에 대해 논의했습니다. (SIPO)시프트 레지스터. 외부로부터 데이터를 직렬 형식으로 받아들이고 'N'비트 데이터를 이동하기 위해 'N'클럭 펄스가 필요합니다.
비슷하게, ‘N’ bit Ring counter유사한 작업을 수행합니다. 그러나 유일한 차이점은 가장 오른쪽 D 플립 플롭의 출력이 외부에서 데이터를 적용하는 대신 가장 왼쪽 D 플립 플롭의 입력으로 제공된다는 것입니다. 따라서 링 카운터는 일련의 상태 (0과 1의 패턴)를 생성하며 매번 반복됩니다.‘N’ clock cycles.
그만큼 block diagram 3 비트 링 카운터의 그림은 다음과 같습니다.
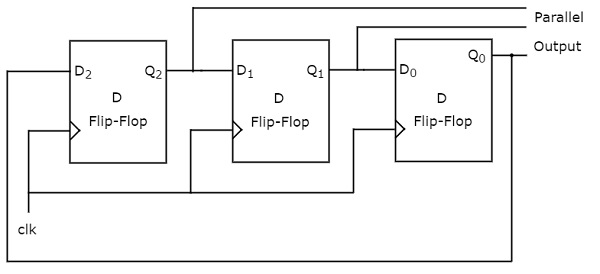
3 비트 링 카운터에는 3 비트 SIPO 시프트 레지스터 만 포함됩니다. 맨 오른쪽 D 플립 플롭의 출력은 맨 왼쪽 D 플립 플롭의 직렬 입력에 연결됩니다.
가장 왼쪽에서 가장 오른쪽으로 D 플립 플롭의 초기 상태는 $Q_{2}Q_{1}Q_{0}=001$. 여기,$Q_{2}$ & $Q_{0}$각각 MSB 및 LSB입니다. 우리는 이해할 수 있습니다working of Ring counter 다음 표에서.
| 클록의 양의 에지 없음 | 직렬 입력 = Q 0 | Q 2 (MSB) | 질문 1 | Q 0 (LSB) |
|---|---|---|---|---|
| 0 | - | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 |
| 삼 | 0 | 0 | 0 | 1 |
클록 신호가 없을 때 D 플립 플롭의 초기 상태는 다음과 같습니다. $Q_{2}Q_{1}Q_{0}=001$. 이 상태는 클록 신호의 양의 에지 전환 3 회마다 반복됩니다.
따라서 다음 operations 클럭 신호의 모든 양의 에지에 대해 발생합니다.
첫 번째 D 플립 플롭의 직렬 입력은 세 번째 플립 플롭의 이전 출력을 가져옵니다. 따라서 첫 번째 D 플립 플롭의 현재 출력은 세 번째 플립 플롭의 이전 출력과 같습니다.
첫 번째 및 두 번째 D 플립 플롭의 이전 출력은 오른쪽으로 1 비트 이동됩니다. 즉, 두 번째 및 세 번째 D 플립 플롭의 현재 출력은 첫 번째 및 두 번째 D 플립 플롭의 이전 출력과 동일합니다.
존슨 링 카운터
운영 Johnson Ring counter링 카운터와 비슷합니다. 그러나 유일한 차이점은 가장 오른쪽 D 플립 플롭의 보완 출력이 정상 출력 대신 가장 왼쪽 D 플립 플롭의 입력으로 제공된다는 것입니다. 따라서 'N'비트 Johnson Ring 카운터는 일련의 상태 (0과 1의 패턴)를 생성하고 모든 상태에 대해 반복합니다.‘2N’ clock cycles.
Johnson Ring 카운터는 Twisted Ring counter테일 링 카운터를 전환합니다. 그만큼block diagram 3 비트 Johnson Ring 카운터의 그림은 다음과 같습니다.

3 비트 Johnson Ring 카운터에는 3 비트 SIPO 시프트 레지스터 만 포함되어 있습니다. 맨 오른쪽 D 플립 플롭의 보완 출력은 맨 왼쪽 D 플립 플롭의 직렬 입력에 연결됩니다.
처음에 모든 D 플립 플롭이 지워 졌다고 가정합니다. 그래서,$Q_{2}Q_{1}Q_{0}=000$. 여기,$Q_{2}$ & $Q_{0}$각각 MSB 및 LSB입니다. 우리는 이해할 수 있습니다working 다음 표에서 Johnson Ring 카운터의
| 클록의 양의 에지 없음 | 직렬 입력 = Q 0 | Q 2 (MSB) | 질문 1 | Q 0 (LSB) |
|---|---|---|---|---|
| 0 | - | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
| 2 | 1 | 1 | 1 | 0 |
| 삼 | 1 | 1 | 1 | 1 |
| 4 | 0 | 0 | 1 | 1 |
| 5 | 0 | 0 | 0 | 1 |
| 6 | 0 | 0 | 0 | 0 |
클록 신호가 없을 때 D 플립 플롭의 초기 상태는 다음과 같습니다. $Q_{2}Q_{1}Q_{0}=000$. 이 상태는 클럭 신호의 6 개의 포지티브 에지 전환마다 반복됩니다.
따라서 다음 operations 클럭 신호의 모든 양의 에지에 대해 발생합니다.
첫 번째 D 플립 플롭의 직렬 입력은 세 번째 플립 플롭의 이전 보완 출력을 가져옵니다. 따라서 첫 번째 D 플립 플롭의 현재 출력은 세 번째 플립 플롭의 이전 보완 출력과 동일합니다.
첫 번째 및 두 번째 D 플립 플롭의 이전 출력은 오른쪽으로 1 비트 이동됩니다. 즉, 두 번째 및 세 번째 D 플립 플롭의 현재 출력은 첫 번째 및 두 번째 D 플립 플롭의 이전 출력과 동일합니다.
이전 두 장에서 다양한 시프트 레지스터 및 counters using D flipflops. 이제 T 플립 플롭을 사용하는 다양한 카운터에 대해 살펴 보겠습니다. 우리는 T 플립 플롭이 클록 신호의 모든 양의 에지 또는 클록 신호의 음의 에지에 대해 출력을 토글한다는 것을 알고 있습니다.
'N'비트 이진 카운터는 'N'T 플립 플롭으로 구성됩니다. 카운터가 0에서 2까지 세는 경우 − 1이면 바이너리로 불린다 up counter. 마찬가지로 카운터가 2부터 카운트 다운하면 − 1에서 0, 그러면 바이너리로 호출됩니다. down counter.
두 가지가있다 types of counters 동기식으로 연결된 플립 플롭을 기반으로합니다.
- 비동기 카운터
- 동기식 카운터
비동기 카운터
플립 플롭이 동일한 클록 신호를 수신하지 않으면 해당 카운터는 다음과 같이 호출됩니다. Asynchronous counter. 시스템 클럭의 출력은 첫 번째 플립 플롭에만 클럭 신호로 적용됩니다. 나머지 플립 플롭은 이전 단계 플립 플롭의 출력에서 클럭 신호를 수신합니다. 따라서 모든 플립 플롭의 출력은 동시에 변경 (영향)되지 않습니다.
이제 다음 두 카운터를 하나씩 살펴 보겠습니다.
- 비동기 바이너리 업 카운터
- 비동기 바이너리 다운 카운터
비동기 바이너리 업 카운터
'N'비트 비동기 바이너리 업 카운터는 'N'T 플립 플롭으로 구성됩니다. 0에서 2까지 계산 − 1. block diagram 3 비트 비동기 바이너리 업 카운터의 그림은 다음과 같습니다.

3 비트 비동기 바이너리 업 카운터에는 3 개의 T 플립 플롭이 포함되어 있으며 모든 플립 플롭의 T 입력은 '1'에 연결됩니다. 이러한 모든 플립 플롭은 네거티브 에지 트리거링되지만 출력은 비동기 적으로 변경됩니다. 클럭 신호는 첫 번째 T 플립 플롭에 직접 적용됩니다. 따라서 첫 번째 T 플립 플롭의 출력은toggles 클럭 신호의 모든 음의 에지에 대해.
첫 번째 T 플립 플롭의 출력은 두 번째 T 플립 플롭의 클럭 신호로 적용됩니다. 따라서 두 번째 T 플립 플롭의 출력은 첫 번째 T 플립 플롭의 출력의 모든 음의 에지에 대해 토글됩니다. 마찬가지로, 세 번째 T 플립 플롭의 출력은 두 번째 T 플립 플롭의 출력의 모든 음의 에지에 대해 토글됩니다. 두 번째 T 플립 플롭의 출력은 세 번째 T 플립 플롭의 클록 신호 역할을하기 때문입니다.
맨 오른쪽에서 맨 왼쪽으로 T 플립 플롭의 초기 상태가 다음과 같다고 가정합니다. $Q_{2}Q_{1}Q_{0}=000$. 여기,$Q_{2}$ & $Q_{0}$각각 MSB 및 LSB입니다. 우리는 이해할 수 있습니다working 다음 표에서 3 비트 비동기 바이너리 카운터의.
| 클럭의 네거티브 에지 없음 | Q 0 (LSB) | 질문 1 | Q 2 (MSB) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 |
| 삼 | 1 | 1 | 0 |
| 4 | 0 | 0 | 1 |
| 5 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 |
| 7 | 1 | 1 | 1 |
여기 $Q_{0}$ 클럭 신호의 모든 음의 에지에 대해 토글됩니다. $Q_{1}$ 매번 토글 $Q_{0}$1에서 0으로, 그렇지 않으면 이전 상태로 유지됩니다. 비슷하게,$Q_{2}$ 매번 토글 $Q_{1}$ 1에서 0으로, 그렇지 않으면 이전 상태로 유지됩니다.
클록 신호가 없을 때 T 플립 플롭의 초기 상태는 다음과 같습니다. $Q_{2}Q_{1}Q_{0}=000$. 이것은 클럭 신호의 모든 음의 에지에 대해 1 씩 증가하고 클럭 신호의 7 번째 음의 에지 에서 최대 값에 도달합니다 . 이 패턴은 클럭 신호의 추가 음의 에지가 적용될 때 반복됩니다.
비동기 바이너리 다운 카운터
'N'비트 비동기 바이너리 다운 카운터는 'N'T 플립 플롭으로 구성됩니다. 2부터 계산 − 1에서 0. block diagram 3 비트 비동기 바이너리 다운 카운터의 그림은 다음과 같습니다.

3 비트 비동기 바이너리 다운 카운터의 블록 다이어그램은 3 비트 비동기 바이너리 업 카운터의 블록 다이어그램과 유사합니다. 그러나 유일한 차이점은 한 단계 플립 플롭의 일반 출력을 다음 단계 플립 플롭의 클록 신호로 연결하는 대신complemented outputs다음 단계 플립 플롭을위한 클럭 신호로 한 단계 플립 플롭의. 보완 출력이 1에서 0으로 이동하는 것은 일반 출력이 0에서 1로 이동하는 것과 동일합니다.
맨 오른쪽에서 맨 왼쪽으로 T 플립 플롭의 초기 상태가 다음과 같다고 가정합니다. $Q_{2}Q_{1}Q_{0}=000$. 여기,$Q_{2}$ & $Q_{0}$각각 MSB 및 LSB입니다. 우리는 이해할 수 있습니다working 다음 표에서 3 비트 비동기 바이너리 다운 카운터의.
| 클럭의 네거티브 에지 없음 | Q 0 (LSB) | 질문 1 | Q 2 (MSB) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 0 | 1 | 1 |
| 삼 | 1 | 0 | 1 |
| 4 | 0 | 0 | 1 |
| 5 | 1 | 1 | 0 |
| 6 | 0 | 1 | 0 |
| 7 | 1 | 0 | 0 |
여기 $Q_{0}$ 클럭 신호의 모든 음의 에지에 대해 토글됩니다. $Q_{1}$ 매번 토글 $Q_{0}$0에서 1로, 그렇지 않으면 이전 상태로 유지됩니다. 비슷하게,$Q_{2}$ 매번 토글 $Q_{1}$ 0에서 1로, 그렇지 않으면 이전 상태로 유지됩니다.
클록 신호가 없을 때 T 플립 플롭의 초기 상태는 다음과 같습니다. $Q_{2}Q_{1}Q_{0}=000$. 이것은 클럭 신호의 모든 음의 에지에 대해 1 씩 감소하고 클럭 신호의 8 번째 음의 에지 에서 동일한 값에 도달합니다 . 이 패턴은 클럭 신호의 추가 음의 에지가 적용될 때 반복됩니다.
동기식 카운터
모든 플립 플롭이 동일한 클럭 신호를 수신하면 해당 카운터는 다음과 같이 호출됩니다. Synchronous counter. 따라서 모든 플립 플롭의 출력이 동시에 변경 (영향)됩니다.
이제 다음 두 카운터를 하나씩 살펴 보겠습니다.
- 동기 바이너리 업 카운터
- 동기 바이너리 다운 카운터
동기 바이너리 업 카운터
'N'비트 동기 바이너리 업 카운터는 'N'T 플립 플롭으로 구성됩니다. 0에서 2까지 계산 − 1. block diagram 3 비트 동기 바이너리 업 카운터의 그림은 다음과 같습니다.

3 비트 동기 바이너리 업 카운터에는 3 개의 T 플립 플롭과 1 개의 2 입력 AND 게이트가 있습니다. 이러한 모든 플립 플롭은 네거티브 에지 트리거되며 플립 플롭의 출력은 동 기적으로 변경 (영향)됩니다. 첫 번째, 두 번째 및 세 번째 플립 플롭의 T 입력은 1입니다.$Q_{0}$ & $Q_{1}Q_{0}$ 각기.
첫 번째 T 플립 플롭의 출력 toggles클럭 신호의 모든 음의 에지에 대해. 두 번째 T 플립 플롭의 출력은 다음과 같은 경우 클록 신호의 모든 음의 에지에 대해 토글됩니다.$Q_{0}$ 세 번째 T 플립 플롭의 출력은 클럭 신호의 모든 네거티브 에지에 대해 토글됩니다. $Q_{0}$ & $Q_{1}$ 1입니다.
동기 바이너리 다운 카운터
'N'비트 동기 바이너리 다운 카운터는 'N'T 플립 플롭으로 구성됩니다. 2부터 계산 − 1에서 0. block diagram 3 비트 동기 바이너리 다운 카운터의 그림은 다음과 같습니다.

3 비트 동기 바이너리 다운 카운터에는 3 개의 T 플립 플롭과 1 개의 2 입력 AND 게이트가 있습니다. 이러한 모든 플립 플롭은 네거티브 에지 트리거되며 플립 플롭의 출력은 동 기적으로 변경 (영향)됩니다. 첫 번째, 두 번째 및 세 번째 플립 플롭의 T 입력은 1입니다.${Q_{0}}'$ & ' ${Q_{1}}'$$각각 {Q_ {0}} '$.
첫 번째 T 플립 플롭의 출력 toggles클럭 신호의 모든 음의 에지에 대해. 두 번째 T 플립 플롭의 출력은 $ {Q_ {0}} '인 경우 클록 신호의 모든 음의 에지에 대해 토글됩니다.$ is 1. The output of third T flip-flop toggles for every negative edge of clock signal if both ${Q_ {1}} '$ & ${Q_ {0}} '$는 1입니다.
동기식 순차 회로는 입력에 따라 클록 신호의 모든 양 (또는 음) 전환에 대해 상태를 변경 (영향)한다는 것을 알고 있습니다. 따라서 동기 순차 회로의 이러한 동작은 그래픽 형식으로 나타낼 수 있으며 다음과 같이 알려져 있습니다.state diagram.
동기 순차 회로는 Finite State Machine(FSM), 유한 수의 상태가있는 경우. FSM에는 두 가지 유형이 있습니다.
- Mealy 스테이트 머신
- 무어 스테이트 머신
이제이 두 상태 머신에 대해 하나씩 논의 해 보겠습니다.
Mealy 스테이트 머신
Finite State Machine은 출력이 현재 입력과 현재 상태에 모두 의존하는 경우 Mealy 상태 시스템이라고합니다. 그만큼block diagram Mealy 상태 머신의 상태는 다음 그림에 나와 있습니다.
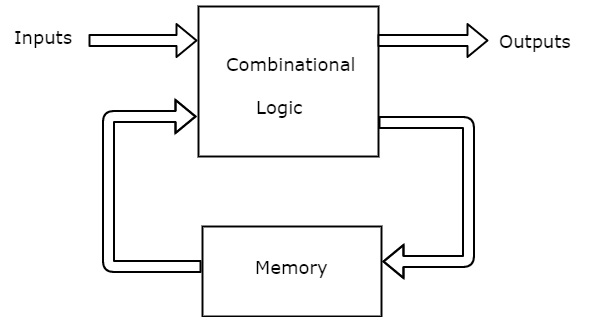
그림에 표시된 것처럼 Mealy 상태 머신에는 두 부분이 있습니다. 그것들은 조합 논리와 기억입니다. 메모리는 이전 출력의 일부 또는 일부를 제공하는 데 유용합니다.(present states) 조합 논리의 입력으로.
따라서 현재 입력 및 현재 상태를 기반으로 Mealy 상태 머신은 출력을 생성합니다. 따라서 출력은 클록 신호의 양 (또는 음) 전환에서만 유효합니다.
그만큼 state diagram Mealy 상태 머신의 상태는 다음 그림에 나와 있습니다.
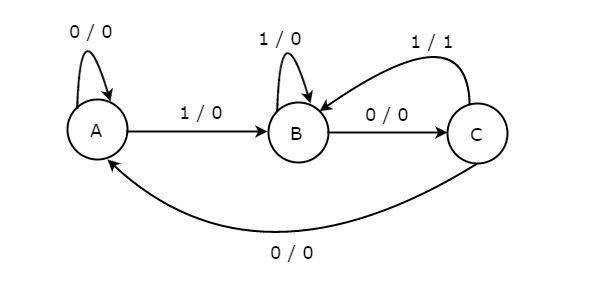
위의 그림에는 A, B, C의 세 가지 상태가 있습니다. 이러한 상태는 원 안에 레이블이 있으며 각 원은 하나의 상태에 해당합니다. 이러한 상태 간의 전환은 방향 선으로 표시됩니다. 여기서 0/0, 1/1, 1/1은input / output. 위의 그림에서 입력 값 x에 따라 각 상태에서 두 번의 전환이 있습니다.
일반적으로 Mealy 상태 시스템에 필요한 상태 수는 Moore 상태 시스템에 필요한 상태 수보다 적거나 같습니다. 각 Mealy 상태 머신에 대해 동등한 Moore 상태 머신이 있습니다.
무어 스테이트 머신
Finite State Machine은 출력이 현재 상태에만 의존하는 경우 Moore 상태 머신이라고합니다. 그만큼block diagram 무어 상태 머신의 모습은 다음 그림과 같습니다.

그림에서 볼 수 있듯이 Moore 상태 시스템에는 두 부분이 있습니다. 그것들은 조합 논리와 기억입니다. 이 경우 현재 입력과 현재 상태가 다음 상태를 결정합니다. 따라서 다음 상태를 기반으로 무어 상태 머신이 출력을 생성합니다. 따라서 출력은 상태가 전환 된 후에 만 유효합니다.
그만큼 state diagram 무어 상태 머신의 모습은 다음 그림과 같습니다.

위의 그림에는 A, B, C, D의 네 가지 상태가 있습니다. 이러한 상태와 각 출력은 원 안에 표시되어 있습니다. 여기서는 입력 값만 각 전환에 레이블이 지정됩니다. 위의 그림에서 입력 값 x에 따라 각 상태에서 두 번의 전환이 있습니다.
일반적으로 Moore 상태 시스템에 필요한 상태 수는 Mealy 상태 시스템에 필요한 상태 수보다 크거나 같습니다. 각 Moore 상태 머신에 대해 동등한 Mealy 상태 머신이 있습니다. 따라서 요구 사항에 따라 그중 하나를 사용할 수 있습니다.
마다 digital system두 부분으로 나눌 수 있습니다. 데이터 경로 (디지털) 회로와 제어 회로입니다. 데이터 경로 회로는 이진 정보 (데이터) 저장 및 한 시스템에서 다른 시스템으로 데이터 전송과 같은 기능을 수행합니다. 반면 제어 회로는 디지털 회로의 작동 흐름을 결정합니다.
상태 다이어그램을 사용하여 대형 상태 머신의 동작을 설명하는 것은 어렵습니다. 이러한 어려움을 극복하기 위해 ASM (Algorithmic State Machine) 차트를 사용할 수 있습니다.ASM charts플로우 차트와 유사합니다. 데이터 경로 회로 및 제어 회로에서 수행 할 작업의 흐름을 나타내는 데 사용됩니다.
ASM 차트의 기본 구성 요소
다음은 ASM 차트의 세 가지 기본 구성 요소입니다.
- 상태 상자
- 결정 상자
- 조건부 출력 상자
상태 상자
상태 상자는 직사각형 모양으로 표시됩니다. 각 상태 상자는 순차 회로의 한 상태를 나타냅니다. 그만큼symbol 상태 상자의 상태는 다음 그림과 같습니다.
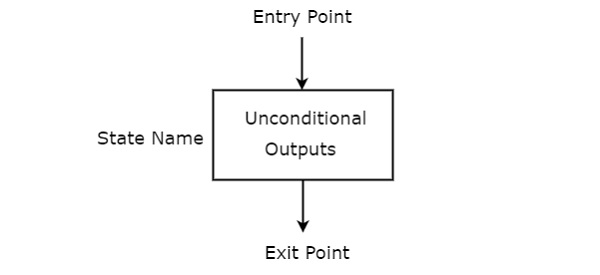
그것은 하나의 진입 지점과 하나의 출구 지점을 가지고 있습니다. 상태 이름은 상태 상자 왼쪽에 배치됩니다. 해당 상태에 해당하는 무조건 출력은 상태 상자 안에 배치 할 수 있습니다.Moore 상태 머신 출력은 상태 상자 안에 배치 할 수도 있습니다.
결정 상자
결정 상자는 다이아몬드 모양으로 표시됩니다. 그만큼symbol 다음 그림은 결정 상자의 내용을 보여줍니다.

하나의 진입 점과 두 개의 출구 경로가 있습니다. 입력 또는 부울 식은 결정 상자 안에 배치 할 수 있으며, 이는 참인지 거짓인지 확인할 수 있습니다. 조건이 참이면 path1을 선호합니다. 그렇지 않으면 path2를 선호합니다.
조건부 출력 상자
조건부 출력 상자는 타원형으로 표시됩니다. 그만큼symbol 조건부 출력 상자의 내용은 다음 그림과 같습니다.

또한 상태 상자와 유사한 하나의 진입 점과 하나의 출구 지점이 있습니다. 조건부 출력은 상태 상자 안에 배치 할 수 있습니다. 일반적으로Mealy상태 머신 출력은 조건부 출력 상자 안에 표시됩니다. 따라서 요구 사항에 따라 위의 구성 요소를 ASM 차트 그리기에 적절하게 사용할 수 있습니다.