Sistemas de controle - Redução do diagrama de blocos
Os conceitos discutidos no capítulo anterior são úteis para reduzir (simplificar) os diagramas de blocos.
Regras de redução do diagrama de blocos
Siga estas regras para simplificar (reduzir) o diagrama de blocos, que tem muitos blocos, pontos de soma e pontos de decolagem.
Rule 1 - Verifique os blocos conectados em série e simplifique.
Rule 2 - Verifique os blocos conectados em paralelo e simplifique.
Rule 3 - Verifique os blocos conectados no loop de feedback e simplifique.
Rule 4 - Se houver dificuldade com o ponto de decolagem durante a simplificação, mude para a direita.
Rule 5 - Se houver dificuldade em somar o ponto durante a simplificação, desloque-o para a esquerda.
Rule 6 - Repita os passos acima até obter a forma simplificada, ou seja, bloco único.
Note - A função de transferência presente neste bloco único é a função de transferência do diagrama de bloco geral.
Exemplo
Considere o diagrama de blocos mostrado na figura a seguir. Vamos simplificar (reduzir) este diagrama de blocos usando as regras de redução do diagrama de blocos.

Step 1- Use a Regra 1 para os blocos $ G_1 $ e $ G_2 $. Use a Regra 2 para os blocos $ G_3 $ e $ G_4 $. O diagrama de blocos modificado é mostrado na figura a seguir.

Step 2- Use a Regra 3 para os blocos $ G_1G_2 $ e $ H_1 $. Use a Regra 4 para mudar o ponto de decolagem após o bloco $ G_5 $. O diagrama de blocos modificado é mostrado na figura a seguir.

Step 3- Use a Regra 1 para os blocos $ (G_3 + G_4) $ e $ G_5 $. O diagrama de blocos modificado é mostrado na figura a seguir.

Step 4- Use a Regra 3 para os blocos $ (G_3 + G_4) G_5 $ e $ H_3 $. O diagrama de blocos modificado é mostrado na figura a seguir.

Step 5- Use a Regra 1 para blocos conectados em série. O diagrama de blocos modificado é mostrado na figura a seguir.

Step 6- Use a Regra 3 para blocos conectados em loop de feedback. O diagrama de blocos modificado é mostrado na figura a seguir. Este é o diagrama de blocos simplificado.
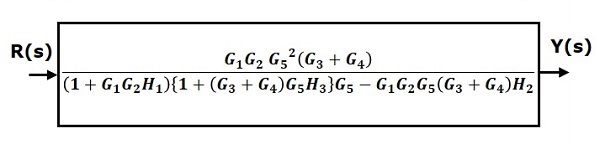
Portanto, a função de transferência do sistema é
$$ \ frac {Y (s)} {R (s)} = \ frac {G_1G_2G_5 ^ 2 (G_3 + G_4)} {(1 + G_1G_2H_1) \ lbrace 1+ (G_3 + G_4) G_5H_3 \ rbrace G_5-G_1G_2G_5 (G_3 + G_4) H_2} $$
Note - Siga estas etapas para calcular a função de transferência do diagrama de blocos com várias entradas.
Step 1 - Encontre a função de transferência do diagrama de blocos considerando uma entrada por vez e torne as entradas restantes como zero.
Step 2 - Repita a etapa 1 para as entradas restantes.
Step 3 - Obtenha a função de transferência geral adicionando todas essas funções de transferência.
O processo de redução do diagrama de blocos leva mais tempo para sistemas complicados. Porque, temos que desenhar o diagrama de blocos (parcialmente simplificado) após cada etapa. Portanto, para superar essa desvantagem, use gráficos de fluxo de sinal (representação).
Nos próximos dois capítulos, discutiremos sobre os conceitos relacionados aos gráficos de fluxo de sinal, ou seja, como representar o gráfico de fluxo de sinal de um dado diagrama de blocos e cálculo da função de transferência apenas usando uma fórmula de ganho sem fazer nenhum processo de redução.