Analogias Elétricas de Sistemas Mecânicos
Dois sistemas são considerados analogous entre si se as duas condições a seguir forem satisfeitas.
- Os dois sistemas são fisicamente diferentes
- A modelagem de equações diferenciais desses dois sistemas são iguais
Os sistemas elétricos e os sistemas mecânicos são dois sistemas fisicamente diferentes. Existem dois tipos de analogias elétricas de sistemas mecânicos translacionais. Essas são analogia da tensão de força e analogia da corrente de força.
Analogia de tensão de força
Na analogia da tensão de força, as equações matemáticas de translational mechanical system são comparados com as equações da malha do sistema elétrico.
Considere o seguinte sistema mecânico translacional, conforme mostrado na figura a seguir.
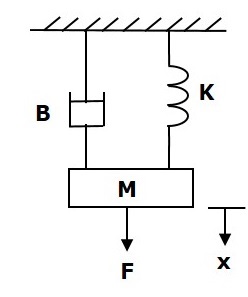
o force balanced equation para este sistema é
$$ F = F_m + F_b + F_k $$
$ \ Rightarrow F = M \ frac {\ text {d} ^ 2x} {\ text {d} t ^ 2} + B \ frac {\ text {d} x} {\ text {d} t} + Kx $ (Equation 1)
Considere o seguinte sistema elétrico, conforme mostrado na figura a seguir. Este circuito consiste em um resistor, um indutor e um capacitor. Todos esses elementos elétricos são conectados em série. A tensão de entrada aplicada a este circuito é $ V $ volts e a corrente que flui através do circuito é $ i $ Amps.

A equação de malha para este circuito é
$ V = Ri + L \ frac {\ text {d} i} {\ text {d} t} + \ frac {1} {c} \ int idt $ (Equation 2)
Substitua, $ i = \ frac {\ text {d} q} {\ text {d} t} $ na Equação 2.
$$ V = R \ frac {\ text {d} q} {\ text {d} t} + L \ frac {\ text {d} ^ 2q} {\ text {d} t ^ 2} + \ frac { q} {C} $$
$ \ Rightarrow V = L \ frac {\ text {d} ^ 2q} {\ text {d} t ^ 2} + R \ frac {\ text {d} q} {\ text {d} t} + \ left (\ frac {1} {c} \ right) q $ (Equation 3)
Comparando a Equação 1 e a Equação 3, obteremos as quantidades análogas do sistema mecânico translacional e do sistema elétrico. A tabela a seguir mostra essas grandezas análogas.
| Sistema Mecânico Translacional | Sistema elétrico |
|---|---|
| Força (F) | Tensão (V) |
| Massa (M) | Indutância (L) |
| Coeficiente de fricção (B) | Resistência (R) |
| Constante de mola (K) | Recíproca de Capacitância $ (\ frac {1} {c}) $ |
| Deslocamento (x) | Carga (q) |
| Velocidade (v) | Atual (i) |
Da mesma forma, há analogia de tensão de torque para sistemas mecânicos rotacionais. Vamos agora discutir sobre essa analogia.
Analogia de tensão de torque
Nesta analogia, as equações matemáticas de rotational mechanical system são comparados com as equações da malha do sistema elétrico.
O sistema mecânico de rotação é mostrado na figura a seguir.

A equação de torque balanceado é
$$ T = T_j + T_b + T_k $$
$ \ Rightarrow T = J \ frac {\ text {d} ^ 2 \ theta} {\ text {d} t ^ 2} + B \ frac {\ text {d} \ theta} {\ text {d} t} + k \ theta $ (Equation 4)
Comparando a Equação 4 e a Equação 3, obteremos as quantidades análogas do sistema mecânico rotacional e do sistema elétrico. A tabela a seguir mostra essas grandezas análogas.
| Sistema Mecânico Rotacional | Sistema elétrico |
|---|---|
| Torque (T) | Tensão (V) |
| Momento de Inércia (J) | Indutância (L) |
| Coeficiente de atrito rotacional (B) | Resistência (R) |
| Constante de mola de torção (K) | Recíproca de Capacitância $ (\ frac {1} {c}) $ |
| Deslocamento Angular (θ) | Carga (q) |
| Velocidade angular (ω) | Atual (i) |
Forçar Analogia Atual
Em vigor a analogia atual, as equações matemáticas do translational mechanical system são comparados com as equações nodais do sistema elétrico.
Considere o seguinte sistema elétrico, conforme mostrado na figura a seguir. Este circuito consiste em fonte de corrente, resistor, indutor e capacitor. Todos esses elementos elétricos são conectados em paralelo.

A equação nodal é
$ i = \ frac {V} {R} + \ frac {1} {L} \ int Vdt + C \ frac {\ text {d} V} {\ text {d} t} $ (Equation 5)
Substitua, $ V = \ frac {\ text {d} \ Psi} {\ text {d} t} $ na Equação 5.
$$ i = \ frac {1} {R} \ frac {\ text {d} \ Psi} {\ text {d} t} + \ left (\ frac {1} {L} \ right) \ Psi + C \ frac {\ text {d} ^ 2 \ Psi} {\ text {d} t ^ 2} $$
$ \ Rightarrow i = C \ frac {\ text {d} ^ 2 \ Psi} {\ text {d} t ^ 2} + \ left (\ frac {1} {R} \ right) \ frac {\ text { d} \ Psi} {\ text {d} t} + \ left (\ frac {1} {L} \ right) \ Psi $ (Equation 6)
Comparando a Equação 1 e a Equação 6, obteremos as quantidades análogas do sistema mecânico translacional e do sistema elétrico. A tabela a seguir mostra essas grandezas análogas.
| Sistema Mecânico Translacional | Sistema elétrico |
|---|---|
| Força (F) | Atual (i) |
| Massa (M) | Capacitância (C) |
| Coeficiente de atrito (B) | Recíproca de resistência $ (\ frac {1} {R}) $ |
| Constante de mola (K) | Recíproca de indutância $ (\ frac {1} {L}) $ |
| Deslocamento (x) | Fluxo Magnético (ψ) |
| Velocidade (v) | Tensão (V) |
Da mesma forma, há uma analogia de corrente de torque para sistemas mecânicos rotacionais. Vamos agora discutir essa analogia.
Analogia da Corrente de Torque
Nesta analogia, as equações matemáticas do rotational mechanical system são comparados com as equações da malha nodal do sistema elétrico.
Comparando a Equação 4 e a Equação 6, obteremos as quantidades análogas do sistema mecânico rotacional e do sistema elétrico. A tabela a seguir mostra essas grandezas análogas.
| Sistema Mecânico Rotacional | Sistema elétrico |
|---|---|
| Torque (T) | Atual (i) |
| Momento de inércia (J) | Capacitância (C) |
| Coeficiente de atrito rotacional (B) | Recíproca de resistência $ (\ frac {1} {R}) $ |
| Constante de mola de torção (K) | Recíproca de indutância $ (\ frac {1} {L}) $ |
| Deslocamento angular (θ) | Fluxo magnético (ψ) |
| Velocidade angular (ω) | Tensão (V) |
Neste capítulo, discutimos as analogias elétricas dos sistemas mecânicos. Essas analogias são úteis para estudar e analisar o sistema não elétrico como o sistema mecânico de um sistema elétrico análogo.