Sistemas de Controle - Análise de Resposta de Tempo
Podemos analisar a resposta dos sistemas de controle tanto no domínio do tempo quanto no domínio da frequência. Discutiremos a análise de resposta de frequência de sistemas de controle em capítulos posteriores. Vamos agora discutir sobre a análise do tempo de resposta dos sistemas de controle.
O que é o tempo de resposta?
Se a saída do sistema de controle para uma entrada varia em relação ao tempo, é chamada de time responsedo sistema de controle. O tempo de resposta consiste em duas partes.
- Resposta transitória
- Resposta de estado estacionário
A resposta do sistema de controle no domínio do tempo é mostrada na figura a seguir.

Aqui, os estados transiente e estável são indicados na figura. As respostas correspondentes a esses estados são conhecidas como respostas transitórias e de estado estacionário.
Matematicamente, podemos escrever a resposta de tempo c (t) como
$$ c (t) = c_ {tr} (t) + c_ {ss} (t) $$
Onde,
- c tr (t) é a resposta transitória
- c ss (t) é a resposta de estado estacionário
Resposta transitória
Após aplicar a entrada ao sistema de controle, a saída leva certo tempo para atingir o estado estacionário. Portanto, a saída estará em estado transiente até que vá para um estado estável. Portanto, a resposta do sistema de controle durante o estado transiente é conhecida comotransient response.
A resposta transitória será zero para grandes valores de 't'. Idealmente, este valor de 't' é infinito e, praticamente, é cinco vezes constante.
Matematicamente, podemos escrever como
$$ \ lim_ {t \ rightarrow \ infty} c_ {tr} (t) = 0 $$
Resposta de estado estacionário
A parte da resposta de tempo que permanece mesmo após a resposta transitória ter valor zero para grandes valores de 't' é conhecida como steady state response. Isso significa que a resposta transitória será zero, mesmo durante o estado estacionário.
Example
Vamos encontrar os termos de estado transiente e estacionário da resposta de tempo do sistema de controle $ c (t) = 10 + 5e ^ {- t} $
Aqui, o segundo termo $ 5e ^ {- t} $ será zero, pois tdenota infinito. Então, este é otransient term. E o primeiro termo 10 permanece igualtse aproxima do infinito. Então, este é osteady state term.
Sinais de teste padrão
Os sinais de teste padrão são impulso, degrau, rampa e parabólico. Esses sinais são usados para saber o desempenho dos sistemas de controle usando o tempo de resposta da saída.
Sinal de Impulso da Unidade
Um sinal de impulso unitário, δ (t) é definido como
$ \ delta (t) = 0 $ para $ t \ neq 0 $
e $ \ int_ {0 ^ -} ^ {0 ^ +} \ delta (t) dt = 1 $
A figura a seguir mostra o sinal de impulso da unidade.

Portanto, o sinal de impulso unitário existe apenas quando 't' é igual a zero. A área deste sinal em pequeno intervalo de tempo em torno de 't' é igual a zero é um. O valor do sinal de impulso unitário é zero para todos os outros valores de 't'.
Sinal de etapa da unidade
Um sinal de etapa unitária, u (t) é definido como
$$ u (t) = 1; t \ geq 0 $$
$ = 0; t <0 $
A figura a seguir mostra o sinal da etapa da unidade.

Portanto, o sinal de passo unitário existe para todos os valores positivos de 't' incluindo zero. E seu valor é um durante este intervalo. O valor do sinal de etapa da unidade é zero para todos os valores negativos de 't'.
Sinal de rampa da unidade
Um sinal de rampa unitário, r (t) é definido como
$$ r (t) = t; t \ geq 0 $$
$ = 0; t <0 $
Podemos escrever o sinal de rampa unitária, $ r (t) $ em termos de sinal de etapa unitária, $ u (t) $ as
$$ r (t) = tu (t) $$
A figura a seguir mostra o sinal de rampa unitária.

Portanto, o sinal de rampa unitária existe para todos os valores positivos de 't' incluindo zero. E seu valor aumenta linearmente em relação a 't' durante este intervalo. O valor do sinal de rampa unitária é zero para todos os valores negativos de 't'.
Sinal Parabólico Unidade
Um sinal parabólico unitário, p (t) é definido como,
$$ p (t) = \ frac {t ^ 2} {2}; t \ geq 0 $$
$ = 0; t <0 $
Podemos escrever o sinal parabólico unitário, $ p (t) $ em termos do sinal de passo unitário, $ u (t) $ as,
$$ p (t) = \ frac {t ^ 2} {2} u (t) $$
A figura a seguir mostra o sinal parabólico da unidade.
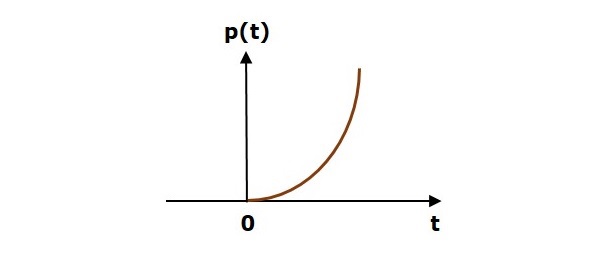
Portanto, o sinal parabólico unitário existe para todos os valores positivos de ‘t’incluindo zero. E seu valor aumenta não linearmente em relação a 't' durante este intervalo. O valor do sinal parabólico unitário é zero para todos os valores negativos de 't'.