Цифровые арифметические схемы
В этой главе давайте обсудим основные арифметические схемы, такие как двоичный сумматор и двоичный вычитатель. Эти схемы могут работать с двоичными значениями 0 и 1.
Двоичный сумматор
Самая основная арифметическая операция - сложение. Схема, которая выполняет сложение двух двоичных чисел, известна какBinary adder. Во-первых, давайте реализуем сумматор, который выполняет сложение двух битов.
Половина сумматора
Полусумматор - это комбинационная схема, которая выполняет сложение двух двоичных чисел A и B из single bit. Он выдает сумму двух выходов, S & carry, C.
В Truth table Полусумматор показан ниже.
| Входы | Выходы | ||
|---|---|---|---|
| А | B | C | S |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Когда мы складываем два бита, результирующая сумма может иметь десятичные значения от 0 до 2. Мы можем представить десятичные цифры 0 и 1 с помощью одного бита в двоичном формате. Но мы не можем представить десятичную цифру 2 с одним битом в двоичном формате. Итак, нам нужны два бита для представления его в двоичном формате.
Пусть сумма, S - младший бит и перенос, C - самый старший бит результирующей суммы. Для первых трех комбинаций входов, перенос, C равен нулю, а значение S будет равно нулю или единице в зависимости отnumber of onesприсутствует на входах. Но для последней комбинации входов, перенос, C равен единице, а сумма, S равна нулю, поскольку результирующая сумма равна двум.
Из таблицы истинности мы можем напрямую записать Boolean functions для каждого выхода как
$$ S = A \ oplus B $$
$ C = AB $
Вышеупомянутые функции можно реализовать с помощью логического элемента Ex-OR с 2 входами и логического элемента AND с 2 входами. Вcircuit diagram Полусумматор показан на следующем рисунке.

В приведенной выше схеме два входных элемента Ex-OR и два входа AND создают сумму, S и перенос, C соответственно. Следовательно, полусумматор выполняет сложение двух битов.
Полный сумматор
Полный сумматор - это комбинационная схема, выполняющая addition of three bitsA, B и C дюйм . Где A и B - два параллельных значащих бита, а C in - бит переноса, который генерируется на предыдущем этапе. Этот полный сумматор также производит два выхода суммы, S & carry, C out , которые аналогичны половинному сумматору.
В Truth table Полный сумматор показан ниже.
| Входы | Выходы | |||
|---|---|---|---|---|
| A | B | Cin | Cout | S |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Когда мы складываем три бита, результирующая сумма может иметь десятичные значения от 0 до 3. Мы можем представить десятичные цифры 0 и 1 с помощью одного бита в двоичном формате. Но мы не можем представить десятичные цифры 2 и 3 одним битом в двоичном формате. Итак, нам нужны два бита для представления этих двух десятичных цифр в двоичном формате.
Пусть сумма, S - младший бит и перенос, C out - самый старший бит результирующей суммы. Значения выходов для всех комбинаций входов в таблице истинности легко заполнить. Просто посчитайтеnumber of onesприсутствовать на входах и записывать эквивалентное двоичное число на выходах. Если C in равно нулю, то таблица истинности полного сумматора такая же, как таблица истинности полусумматора.
Мы получим следующее Boolean functions для каждого выхода после упрощения.
$$ S = A \ oplus B \ oplus C_ {in} $$
$ c_ {out} = AB + \ left (A \ oplus B \ right) c_ {in} $
Сумма S равна единице, когда на входах присутствует нечетное количество единиц. Мы знаем, что вентиль Ex-OR производит вывод, что является нечетной функцией. Таким образом, мы можем использовать либо два логических элемента Ex-OR с 2 входами, либо один элемент Ex-OR с 3 входами для получения суммы S. Мы можем реализовать перенос C , используя два логических элемента AND с 2 входами и один вентиль OR. Вcircuit diagram Полный сумматор показан на следующем рисунке.
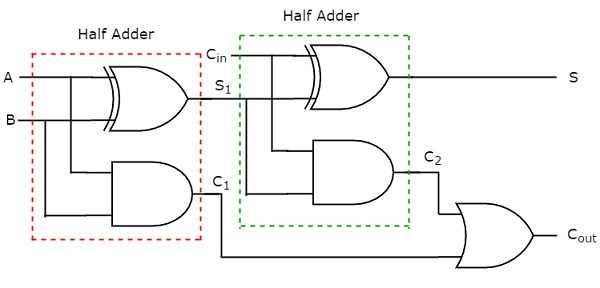
Этот сумматор называется Full adderпотому что для реализации одного полного сумматора нам требуются два полусумматора и один вентиль ИЛИ. Если C in равно нулю, тогда полный сумматор становится половинным сумматором. В этом легко убедиться по приведенной выше принципиальной схеме или по булевым функциям выходов полного сумматора.
4-битный двоичный сумматор
4-битный двоичный сумматор выполняет addition of two 4-bit numbers. Пусть 4-битные двоичные числа, $ A = A_ {3} A_ {2} A_ {1} A_ {0} $ и $ B = B_ {3} B_ {2} B_ {1} B_ {0} $. Мы можем реализовать 4-битный двоичный сумматор одним из двух следующих способов.
Используйте один полусумматор для добавления двух младших разрядов и три полных сумматора для добавления трех старших значащих битов.
Для единообразия используйте четыре полных сумматора. Поскольку начальный перенос C in равен нулю, полный сумматор, который используется для добавления младших битов, становится полусумматором.
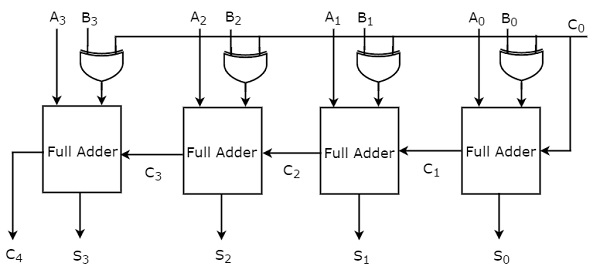
Пока мы рассматривали второй подход. Вblock diagram 4-битного двоичного сумматора показан на следующем рисунке.

Здесь 4 полных сумматора соединены каскадом. Каждый полный сумматор получает соответствующие биты двух параллельных входов A и B. Выход переноса одного полного сумматора будет входом переноса последующего полного сумматора более высокого порядка. Этот 4-битный двоичный сумматор дает результирующую сумму, содержащую не более 5 бит. Итак, выполнением последнего этапа Полный сумматор будет MSB.
Таким образом, мы можем реализовать любой двоичный сумматор более высокого порядка, просто каскадируя необходимое количество полных сумматоров. Этот двоичный сумматор также называютripple carry (binary) adder потому что перенос распространяется (колеблется) от одного этапа к следующему.
Бинарный вычитатель
Схема, которая выполняет вычитание двух двоичных чисел, известна как Binary subtractor. Мы можем реализовать двоичный вычитатель следующими двумя способами.
- Каскад Полные вычитатели
- 2 метод дополнения
В первом методе мы получим n-битный двоичный вычитатель путем каскадирования n полных вычитателей. Итак, сначала вы можете реализовать половинный вычитатель и полный вычитатель, аналогичные полусумматору и полному сумматору. Затем вы можете реализовать n-битный двоичный вычитатель путем каскадирования n полных вычитателей. Итак, у нас будут две отдельные схемы для двоичного сложения и вычитания двух двоичных чисел.
Во втором методе мы можем использовать тот же двоичный сумматор для вычитания двух двоичных чисел, просто сделав некоторые изменения во втором вводе. Таким образом, выполняется внутренняя операция двоичного сложения, но на выходе получается вычитание.
Мы знаем, что вычитание двух двоичных чисел A и B может быть записано как,
$$ AB = A + \ left ({2} 's \: комплимент \: of \: B \ right) $$
$ \ Rightarrow AB = A + \ left ({1} \: дополнение \: of \: B \ right) + 1 $
4-битный двоичный вычитатель
4-битный двоичный вычитатель производит subtraction of two 4-bit numbers. Пусть 4-битные двоичные числа, $ A = A_ {3} A_ {2} A_ {1} A_ {0} $ и $ B = B_ {3} B_ {2} B_ {1} B_ {0} $. Внутренне работа 4-битного двоичного вычитателя аналогична работе 4-битного двоичного сумматора. Если обычные биты двоичного числа A, дополненные биты двоичного числа B и начальный перенос (заимствование), C in как один применяются к 4-битному двоичному сумматору, то он становится 4-битным двоичным вычитателем. Вblock diagram 4-битного двоичного вычитателя показано на следующем рисунке.

Этот 4-битный двоичный вычитатель дает на выходе не более 5 битов. Если двоичное число A больше двоичного числа B, то старший бит вывода равен нулю, а оставшиеся биты содержат величину AB. Если двоичное число A меньше двоичного числа B, то старший бит вывода равен единице. Итак, возьмите два дополнения вывода, чтобы получить величину AB.
Таким образом, мы можем реализовать любой двоичный вычитатель более высокого порядка, просто каскадируя необходимое количество полных сумматоров с необходимыми изменениями.
Двоичный сумматор / вычитатель
Схема, которая может использоваться для выполнения сложения или вычитания двух двоичных чисел в любое время, известна как Binary Adder / subtractor. И двоичный сумматор, и двоичный вычитатель содержат набор полных сумматоров, которые соединяются каскадом. Входные биты двоичного числа A напрямую применяются как в двоичном сумматоре, так и в двоичном вычитателе.
Есть два различия во входах полных сумматоров, которые присутствуют в двоичном сумматоре и двоичном вычитателе.
Входные биты двоичного числа B напрямую применяются к полным сумматорам в двоичном сумматоре, тогда как дополненные биты двоичного числа B применяются к полным сумматорам в двоичном вычитателе.
Начальный перенос C 0 = 0 применяется в 4-битном двоичном сумматоре, тогда как начальный перенос (заимствование) C 0 = 1 применяется в 4-битном двоичном вычитателе.
Мы знаем, что 2-input Ex-OR gateпроизводит вывод, который совпадает с выводом первого ввода, когда другой ввод равен нулю. Точно так же он производит вывод, который является дополнением первого ввода, когда другой ввод является одним.
Следовательно, мы можем применить входные биты двоичного числа B к логическим элементам Ex-OR с 2 входами. Другой вход для всех этих вентилей Ex-OR - C 0 . Таким образом, на основе значения C 0 вентили Ex-OR производят либо нормальные, либо дополненные биты двоичного числа B.
4-битный двоичный сумматор / вычитатель
4-битный двоичный сумматор / вычитатель производит сложение или вычитание двух 4-битных чисел на основе значения начального переноса или заимствования, 0 . Пусть 4-битные двоичные числа, $ A = A_ {3} A_ {2} A_ {1} A_ {0} $ и $ B = B_ {3} B_ {2} B_ {1} B_ {0} $. Работа 4-битного двоичного сумматора / вычитателя аналогична работе 4-битного двоичного сумматора и 4-битного двоичного вычитателя.
Примените обычные биты двоичных чисел A и B и начальный перенос или заимствование C 0 извне к 4-битному двоичному сумматору. Вblock diagram 4-битного двоичного сумматора / вычитателя показан на следующем рисунке.
Если начальный перенос 0 равен нулю, тогда каждый полный сумматор получает нормальные биты двоичных чисел A и B. Таким образом, 4-битный двоичный сумматор / вычитатель производит выходной сигнал, который являетсяaddition of two binary numbers А и Б.
Если начальное заимствование, 0 равно единице, то каждый полный сумматор получает нормальные биты двоичного числа A и дополненные биты двоичного числа B. Итак, 4-битный двоичный сумматор / вычитатель производит вывод, который являетсяsubtraction of two binary numbers А и Б.
Следовательно, с помощью дополнительных вентилей Ex-OR одна и та же схема может использоваться как для сложения, так и для вычитания двух двоичных чисел.