Цифровые схемы - пороговая логика
В предыдущих главах мы реализовали различные комбинационные схемы с использованием логических вентилей. За исключением элемента НЕ, остальные все логические элементы имеют как минимум два входа и один выход. Точно так жеthreshold gate также содержит как минимум один вход и только один выход.
Кроме того, он содержит соответствующие веса для каждого входа и пороговое значение. Значения этих весов и порога могут иметь любое конечное действительное число.
Основы порогового гейта
Пусть входы порогового элемента - X 1 , X 2 , X 3 ,…, X n . Соответствующие веса этих входов: W 1 , W 2 , W 3 ,…, W n . Вsymbol Порогового затвора показано на следующем рисунке.
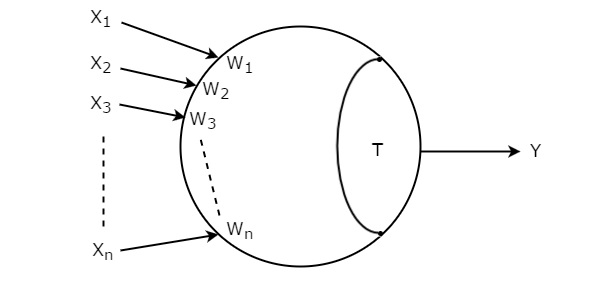
Threshold gateпредставлен в виде круга и имеет «n» входов, от X 1 до X n, и единственный выход, Y. Этот круг состоит из двух частей. Одна часть представляет собой веса, соответствующие входам, а другая часть представляет пороговое значение T.
Сумма произведений входов с соответствующими весами известна как weighted sum. Если эта взвешенная сумма больше или равна пороговому значению T, то только выход Y будет равен единице. В противном случае выход Y будет равен нулю.
Mathematically, мы можем записать эту связь между входами и выходами порогового вентиля, как показано ниже.
$$ Y = 1, если \: \: W_ {1} X_ {1} + W_ {2} X_ {2} + W_ {3} X_ {3} + ... W_ {n} X_ {n} \ geq T $$
= 0 в противном случае.
Следовательно, мы можем реализовать различные логические элементы и булевы функции, просто изменив значения весов и / или порогового значения T.
пример
Давайте найдем simplified Boolean function для следующих пороговых ворот.

Этот пороговый вентиль имеет три входа X 1 , X 2 , X 3 и один выход Y.
Веса, соответствующие входам X 1 , X 2 и X 3, равны W 1 = 2, W 2 = 1 и W 3 = -4 соответственно.
Значение порогового строба T = -1.
В weighted sum порога ворот
$$ W = W_ {1} X_ {1} + W_ {2} X_ {2} + W_ {3} X_ {3} $$
Подставьте указанные веса в приведенное выше уравнение.
$$ \ Rightarrow W = 2X_ {1} + X_ {2} -4X_ {3} $$
На выходе порогового вентиля Y будет «1», если W ≥ −1, в противном случае - «0».
Продолжение table показывает взаимосвязь между входом и выходом для всех возможных комбинаций входов.
| Входы | Взвешенная сумма | Вывод | ||
|---|---|---|---|---|
| $ X_ {1} $ | $ X_ {2} $ | $ X_ {3} $ | $ W = 2X_ {1} + X_ {2} -4X_ {3} $ | $ Y $ |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | -4 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | -3 | 0 |
| 1 | 0 | 0 | 2 | 1 |
| 1 | 0 | 1 | -2 | 0 |
| 1 | 1 | 0 | 3 | 1 |
| 1 | 1 | 1 | -1 | 1 |
Из приведенной выше таблицы мы можем написать Boolean function для вывода Y как
$$ Y = \ sum m \ left (0,2,4,6,7 \ right) $$
Упрощение этой логической функции с использованием 3 variable K-Map показано на следующем рисунке.

Следовательно simplified Boolean function для заданного порогового значения: $ Y = {X_ {3} '} + X_ {1} X_ {2} $.
Синтез пороговых функций.
Пороговый вентиль также называют universal gateпотому что мы можем реализовать любую логическую функцию с помощью пороговых вентилей. Иногда может оказаться невозможным реализовать несколько логических вентилей и логических функций с помощью одного порогового вентиля. В этом случае нам может потребоваться несколько пороговых ворот.
Следуйте этим steps для реализации логической функции с использованием одного порогового вентиля.
Step 1 - Сформулируйте Truth table для данной логической функции.
Step 2 - В приведенной выше таблице истинности добавьте (включите) еще один столбец, который показывает связь между weighted sums и Threshold value.
Step 3 - Запишите соотношение между взвешенными суммами и порогом для каждой комбинации входных данных, как указано ниже.
Если выход логической функции равен 1, то взвешенная сумма будет больше или равна пороговому значению для этой комбинации входов.
Если выход логической функции равен 0, то взвешенная сумма будет меньше порогового значения для этой комбинации входов.
Step 4 - Выберите значения весов и порога таким образом, чтобы они удовлетворяли всем отношениям, представленным в последнем столбце приведенной выше таблицы.
step 5 - Нарисуйте symbol порогового строба с этими весами и пороговым значением.
пример
Реализуем следующие Boolean function с использованием одинарного порогового гейта.
$$ Y \ left (X_ {1}, X_ {2}, X_ {3} \ right) = \ sum m \ left (0,2,4,6,7 \ right) $$
Данная логическая функция представляет собой функцию трех переменных, которая представлена в виде суммы минимальных членов. ВTruth table этой функции показано ниже.
| Входы | Вывод | ||
|---|---|---|---|
| X1 | X2 | X3 | Y |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Теперь давайте добавим (включим) еще один столбец в приведенную выше таблицу истинности. Последний столбец содержит отношения междуweighted sums (W) and Threshold значение (T) для каждой комбинации входов.
| Входы | Вывод | Отношения между W&T | ||
|---|---|---|---|---|
| X1 | X2 | X3 | Y | |
| 0 | 0 | 0 | 1 | 0 ≥T |
| 0 | 0 | 1 | 0 | W 3 <T |
| 0 | 1 | 0 | 1 | W 2 ≥ T |
| 0 | 1 | 1 | 0 | W 2 + W 3 <Т |
| 1 | 0 | 0 | 1 | W 1 ≥ T |
| 1 | 0 | 1 | 0 | W 1 + W 3 <Т |
| 1 | 1 | 0 | 1 | W 1 + W 2 ≥ Т |
| 1 | 1 | 1 | 1 | W 1 + W 2 + W 3 ≥ Т |
Ниже приведены выводы из приведенной выше таблицы.
Значение порога должно быть либо нулевым, либо отрицательным в зависимости от первого отношения.
Значение W 3 должно быть отрицательным на основании первого и второго соотношений.
Значения W 1 и W 2 должны быть больше или равны пороговому значению на основе пятого и третьего соотношений.
W 2 должен быть больше W 3 на основании четвертого соотношения.
Мы можем выбрать следующие значения для весов и пороговых значений на основе сделанных выше выводов.
W 1 = 2, W 2 = 1, W 3 = -4 и T = -1
В symbol Порогового строба с указанными выше значениями показано ниже.

Следовательно, этот пороговый вентиль реализует данный Boolean function, $ Y \ left (X_ {1}, X_ {2}, X_ {3} \ right) = \ sum m \ left (0,2,4,6,7 \ right) $.