Цифровые схемы - конечные машины

Мы знаем, что синхронные последовательные схемы изменяют (влияют) на свои состояния при каждом положительном (или отрицательном) переходе тактового сигнала в зависимости от входного сигнала. Таким образом, это поведение синхронных последовательных цепей может быть представлено в графической форме и известно какstate diagram.

Синхронная последовательная схема также называется Finite State Machine(Автомат), если он имеет конечное число состояний. Есть два типа конечных автоматов.

• Конечный автомат Мили
• Конечный автомат Мура

Теперь давайте поговорим об этих двух конечных автоматах один за другим.

Конечный автомат Мили

Конечный автомат называется конечным автоматом Мили, если выходы зависят как от текущих входов, так и от текущих состояний. Вblock diagram Конечный автомат Мили показан на следующем рисунке.

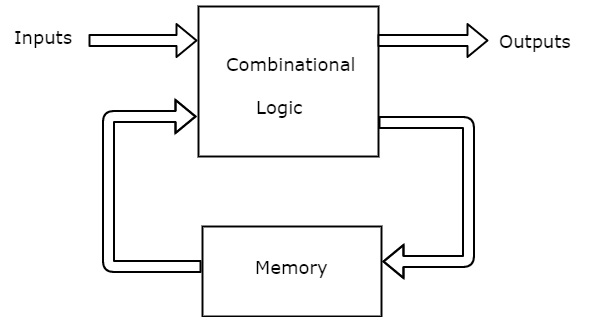
Как показано на рисунке, в конечном автомате Мили присутствуют две части. Это комбинационная логика и память. Память полезна для предоставления некоторых или части предыдущих результатов(present states) как входы комбинационной логики.

Итак, на основе текущих входных данных и текущих состояний конечный автомат Мили выдает выходные данные. Следовательно, выходы будут действительны только при положительном (или отрицательном) переходе тактового сигнала.

В state diagram Конечный автомат Мили показан на следующем рисунке.

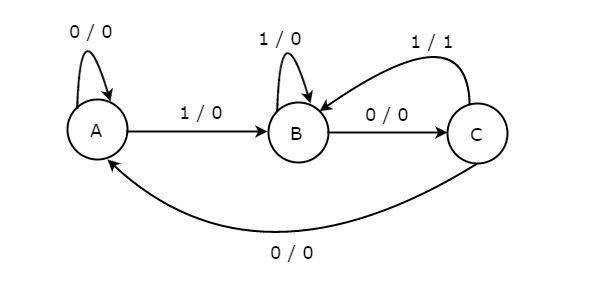
На приведенном выше рисунке есть три состояния, а именно A, B и C. Эти состояния помечены внутри кружков, и каждый кружок соответствует одному состоянию. Переходы между этими состояниями изображены направленными линиями. Здесь 0/0, 1/0 и 1/1 обозначаютinput / output. На приведенном выше рисунке есть два перехода из каждого состояния в зависимости от значения ввода x.

В общем, количество состояний, требуемых в конечном автомате Мили, меньше или равно количеству состояний, необходимых для конечного автомата Мура. Для каждого конечного автомата Мили существует эквивалентный конечный автомат Мура.

Конечный автомат Мура

Конечный автомат называется конечным автоматом Мура, если выходные данные зависят только от текущих состояний. Вblock diagram Конечный автомат Мура показан на следующем рисунке.

Как показано на рисунке, в конечном автомате Мура присутствуют две части. Это комбинационная логика и память. В этом случае текущие входные данные и текущие состояния определяют следующие состояния. Итак, на основе следующих состояний конечный автомат Мура производит выходные данные. Следовательно, выходы будут действительны только после перехода из состояния.

В state diagram Конечный автомат Мура показан на следующем рисунке.

На приведенном выше рисунке есть четыре состояния, а именно A, B, C и D. Эти состояния и соответствующие выходы помечены внутри кружков. Здесь на каждом переходе помечено только входное значение. На приведенном выше рисунке есть два перехода из каждого состояния в зависимости от значения ввода x.

В общем, количество состояний, требуемых в конечном автомате Мура, больше или равно количеству состояний, необходимых для конечного автомата Мили. Для каждого конечного автомата Мура существует эквивалентный конечный автомат Мили. Итак, исходя из требований, мы можем использовать один из них.